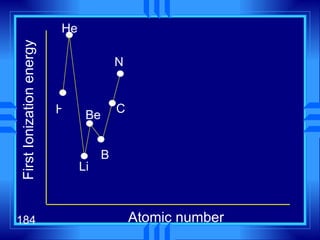
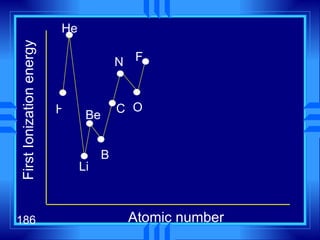
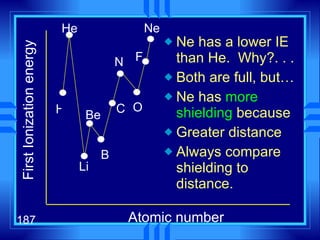
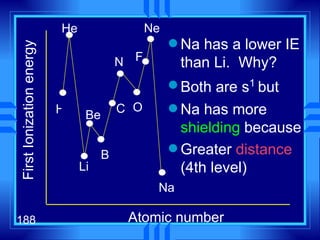
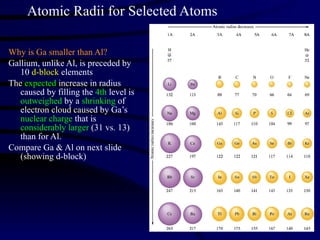
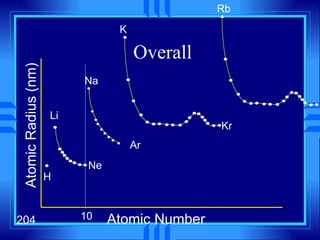
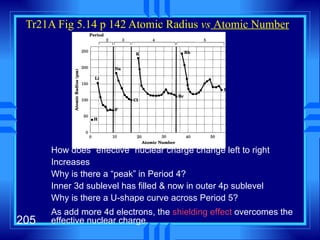
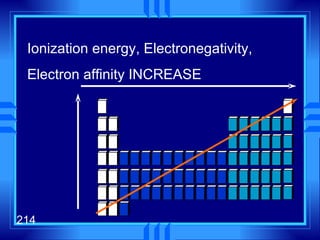
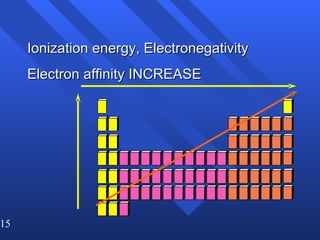
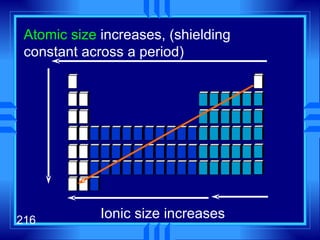
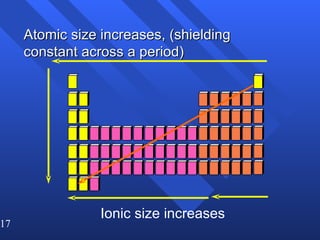
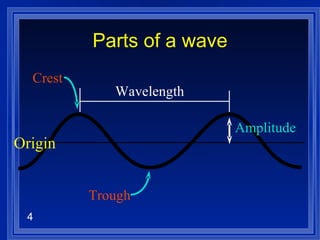
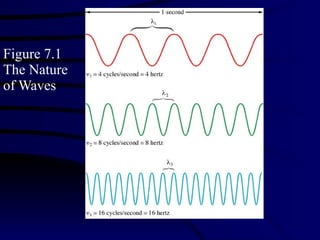
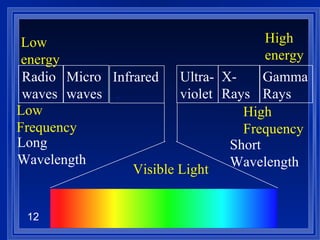
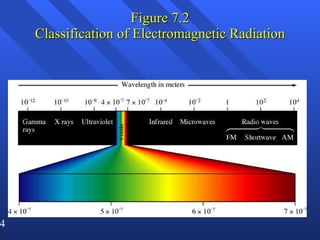
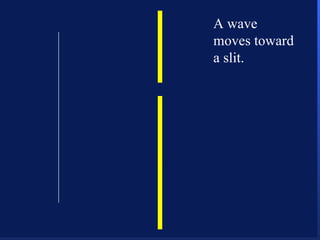
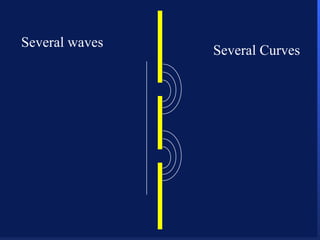
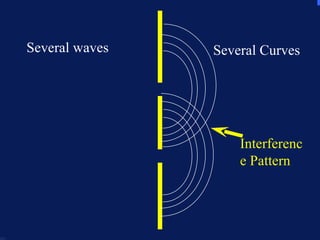
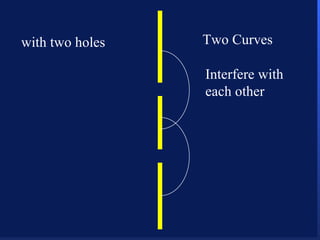
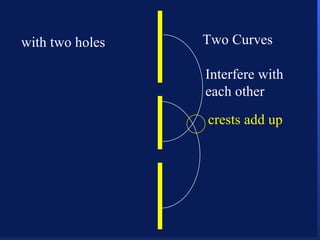
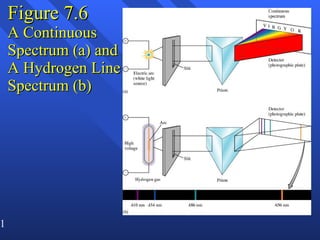
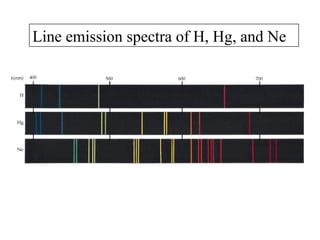
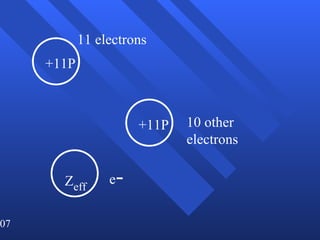
This document summarizes key concepts from a chapter on atomic structure: 1. Electromagnetic radiation consists of oscillating electric and magnetic fields that propagate as waves. Light is a type of electromagnetic radiation detectable by the human eye. 2. Atoms can only absorb or emit electromagnetic radiation at specific quantized energy levels. This explains the emission spectrum of hydrogen, which shows only certain discrete wavelengths. 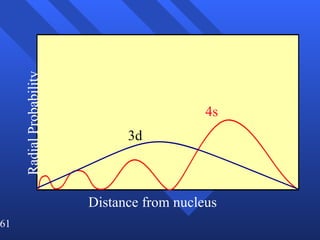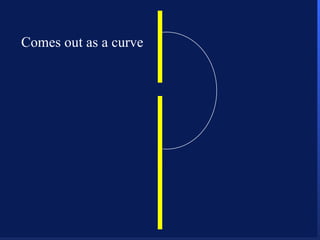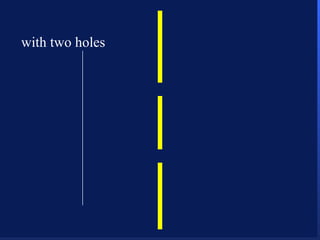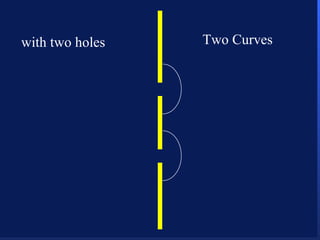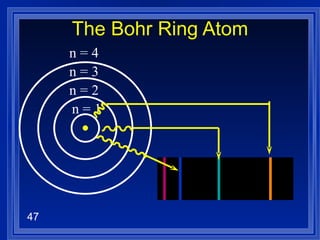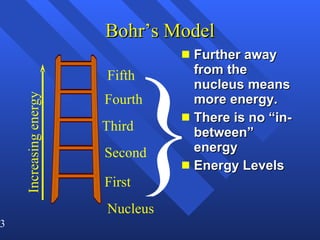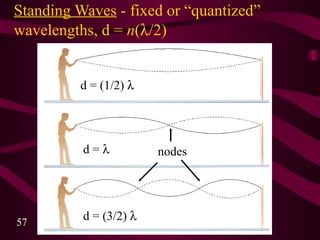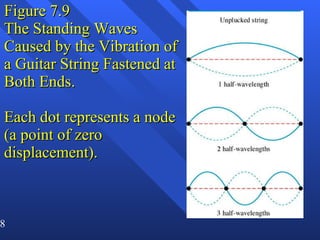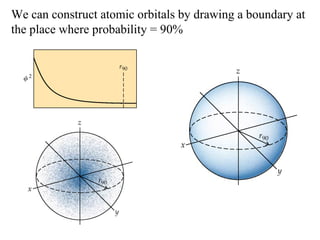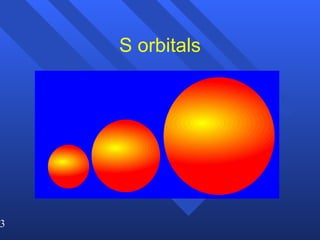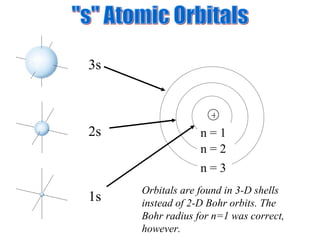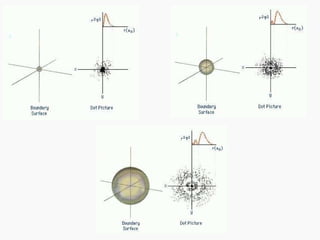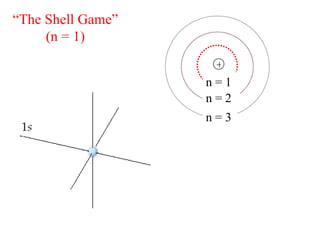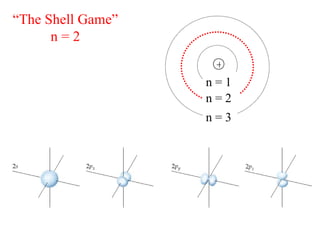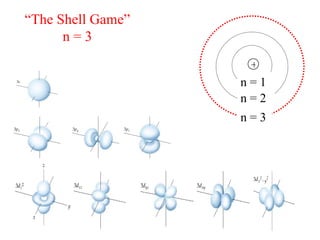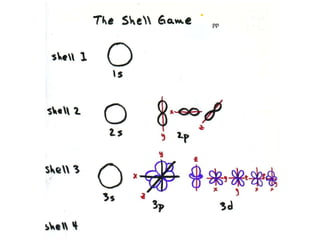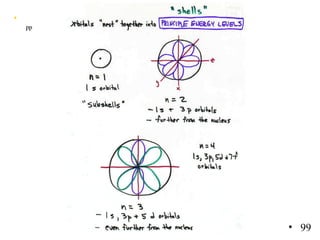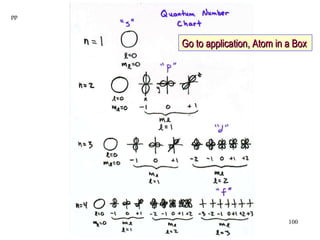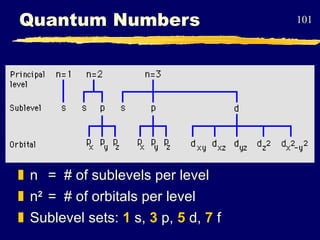3. Niels Bohr's early model of the hydrogen atom proposed that electrons orbit the nucleus at fixed distances corresponding to discrete energy levels. Later, the quantum mechanical model described electron behavior as wave-like standing waves. 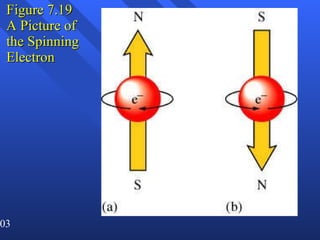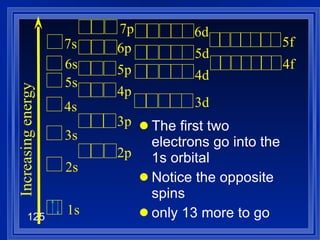4. Werner Heisenberg's uncertainty principle states that the more precisely the position

1. Chapter 7 Atomic Structure pp

2. 7.1 Electromagnetic Radiation Light is made up of electromagnetic radiation . Waves of electric and magnetic fields at right angles to each other. LD 1: 4-1 Electromagnetic radiation

3. Electromagnetic Radiation Mutually propagating electric and magnetic fields, at right angles to each other, traveling at the speed of light c

4. Parts of a wave Origin Wavelength Amplitude Crest Trough

5. Parts of Wave Origin - the base line of the energy. Crest - high point on a wave Trough - Low point on a wave Amplitude - distance from origin to crest Wavelength - distance from crest to crest Wavelength - is abbreviated   Greek letter lambda .

6. Parts of a wave  Wavelength Frequency = number of cycles in one second Measured in hertz 1 hertz = 1 cycle/second

7. Frequency The number of waves that pass a given point per second . Units are cycles/sec or hertz ( Hz ) Abbreviated   the Greek letter nu c =   

8. Frequency and wavelength Are inversely related As one goes up the other goes down. Speed is constant! (Tricky) In a vacuum it is 3.00 x 10 8 m /s or 3.00 x 10 10 cm /s Memorize both . Also, 1 m = 1 x 10 9 nm = 1 x 10 10 Å (angstrom)

9. Frequency = 

10. Figure 7.1 The Nature of Waves

11. Kinds of EM waves There are many different  and  Radio waves, microwaves, x rays and gamma rays are all examples. Light is only the part our eyes can detect. G a m m a R a y s R a d i o w a v e s

12. Radio waves Microwaves Infrared . Ultra-violet X-Rays Gamma Rays Long Wavelength Short Wavelength Visible Light Low energy High energy Low Frequency High Frequency

13. Electromagnetic Spectrum Which has longer  , ultraviolet or gamma rays? UV rays Which has shorter wavelength, microwave or infrared? Microwave

14. Figure 7.2 Classification of Electromagnetic Radiation

15. The speed of light In a vacuum is 2.998 x 10 8 m/s = c c =   What is the wavelength of light with a frequency 5.89 x 10 5 Hz? Ans . . . 509 m (using 2.998 x 10 8 m/s) What is the frequency of blue light with a wavelength of 484 nm ? 6.19 x 10 14 Hz

16. 7.2 The Nature of Matter In 1900 Matter and energy were seen as different from each other in fundamental ways. It was thought that matter was particles. It was thought that energy could come in waves, with any frequency . Max Planck found the cooling of hot objects could not be explained by viewing energy as a wave.

17. The Photoelectric Effect Photoelectric Effect - the emission of electrons from a metal when light shines on it.

18. Tr 19 Fig 4.3 p. 93 Photoelectric Effect

19. The Photoelectric Effect Problem What was predicted . . . Wave theory said light of any   would have enough energy to eject an electrons. What was observed . . . For a given metal, no e- are emitted if   is below a certain frequency no matter how long the light shines . The explanation . . .

20. Light is a Particle as well as a Wave Energy is quantized . Light is energy Light must be quantized These smallest pieces of light are called photons . Energy and frequency are directly related.

21. Energy is Quantized Planck found  E came in chunks with size h   E = nh  where n is an integer and h is Planck’s constant h = 6.626 x 10 -34 J•s 1 joule = 1 Kg m 2 /s 2 (know this!) these packets of h  are called quanta (singular = quantum)

22. Einstein is next He said electromagnetic radiation is quantized in particles called photons . Each photon has energy E= h  = hc/  Combine this with E = mc 2 mc 2 = hc/  You get the apparent mass of a photon. m = h / (  c)

23. Which is Energy? Is energy a wave like light, or a particle? Both. Concept is called the Wave-Particle duality. What about the other way, is matter a wave? Yes

24. Figure 7.4 Electromagnetic Radiation

25. Matter as a wave Using the velocity v instead of the speed of light c we get. . . De Broglie’s equation  = h/mv Mass in this equation is in kg (not g!) Remember this! You have an online HW question that uses this equation. Can calculate the wavelength of an object.

26. Examples pp The laser light of a CD player is 7.80 x 10 2 m. What is the frequency ? Answer . . . C =   so  = c/  = 3.84 x 10 5 Hz What is the energy of a photon of this light? E = h  E = 2.55 x 10 -28 J What is the apparent mass for this photon? apparent mass = h/  c = 2.83 x10 -45 kg What is the energy of a mole of photons? E of mole in (c) above = (h/  c) x Avogadro's number = 1.54 x 10 -4 J/mol

27. What is the wavelength? Of an electron with a mass of 9.11 x 10 -31 kg traveling at 1.0 x 10 7 m/s? Note: all e - s have same mass & 1 joule = 1 Kg m 2 /s 2 Use  = h/mv to get . . . 7.27 x 10 -11 m for the electron Of a softball with a mass of 0.10 kg moving at 125 mi/hr ? Same equation to get . . . 1.9 x 10 -34 m for the ball (Compare to electron)

28. Diffraction When light passes through, or reflects off, a series of thinly spaced lines, it creates a rainbow effect. This is because the waves interfere with each other. LD 1: 4.14

29. A wave moves toward a slit.

30. Comes out as a curve

31. with two holes

32. with two holes Two Curves

33. Two Curves with two holes Interfere with each other

34. Two Curves with two holes Interfere with each other crests add up

35. Several waves

36. Several waves Several Curves

37. Several waves Several waves Interference Pattern Several Curves

38. What will an electron do if diffracted? It has mass , so it is matter. A particle can only go through one hole. A wave can go through both holes. An electron does go though both, and makes an interference pattern . It behaves like a wave. Other matter have wavelengths too short to notice.

39. Figure 7.5 The Constructive and Destructive Interference of Waves Diffraction occurs when electromagnetic radiation is scattered from a regular array such as NaCl crystals. Bright spots from constructive interference of waves. Dark areas from destructive interference.

40. Spectrum The range of frequencies present in light. White light has a continuous spectrum. All the colors are possible. A rainbow.

41. Figure 7.6 A Continuous Spectrum (a) and A Hydrogen Line Spectrum (b)

42. 7.3 Atomic Spectrum of Hydrogen Emission spectrum because these are the colors it gives off or emits . LD1: 4.7 Called a line spectrum. Each element has a unique one. Like a fingerprint. There are just a few discrete lines showing 410 nm 434 nm 486 nm 656 nm

43. Line emission spectra of H, Hg, and Ne

44. What this means Only certain energies are allowed for the electron in an hydrogen atom. Can only give off certain energies. Use  E = h  = hc /  Energy in the in the atom is quantized . This is where we get quantum theory.

45. 7.4 The Bohr Model Niels Bohr developed the quantum model of the hydrogen atom. He said electrons move like planets around the sun (later found incomplete) . Only works for hydrogen electron & other mono electronic species (e.g., He 1+ ion). The electrons were attracted to the nucleus because of opposite charges. Did not fall in to the nucleus because they were moving around very rapidly .

46. The Bohr Ring Atom He didn’t know why but only certain energies were allowed. He called these allowed energies energy levels . Putting energy into the atom moved the electron away from the nucleus. From ground state to excited state. When it returns to ground state it gives off light of a certain energy. LD 1: 4.9

47. The Bohr Ring Atom n = 3 n = 4 n = 2 n = 1

48. The Bohr Model n is the energy level for each energy level the energy is: E = -2.178 x 10 -18 J (Z 2 / n 2 ) Z is the nuclear charge, which is +1 for hydrogen (+2 for He 1 + ion, etc.). n = 1 is called the ground state when the electron is removed, n = ∞ E = 0

49. We are worried about the change When the electron moves from one energy level to another in an H atom (I.e., Z = 1).  E = E final - E initial  E = -2.178 x 10 -18 J Z 2 (1/ n f 2 - 1/ n i 2 ) Use for monoelectronic species only (e.g. He 1+ ion)

50. Examples if time  E = -2.178 x 10 -18 J Z 2 (1/ n f 2 - 1/ n i 2 ) Calculate the energy needed to move a hydrogen electron from its first level to the third energy level. Ans. . . 1.936 x 10 -18 Joules Calculate the E released when an electron moves from n= 4 to n=2 in a hydrogen atom. -4.084 x 10 -19 Joules (negative value means energy released ) Calculate the E released when an e- moves from n= 5 to n=3 in a He +1 ion ( monoelectronic species ) -6.195 x 10 -19 Joules (negative value means energy released )

51. When is it true? Only for hydrogen atoms and other monoelectronic species. Why the negative sign? To decrease the energy of the electron (i.e., the system) you make it closer to the nucleus. the maximum energy an electron can have is zero, at an infinite distance.

52. When is it true? Model correctly fits the quantitized energy levels of H atom and postulates only certain allowed circular orbits for the electron. As e- becomes more tightly bound, its energy becomes more negative relative to the zero-energy reference state (corresponding to the e- being at infinite distance from the nucleus). As e- is brought closer to nucleus, energy is released from the system.

53. Bohr’s Model Further away from the nucleus means more energy. There is no “in-between” energy Energy Levels Increasing energy Nucleus First Second Third Fourth Fifth }

54. The Bohr Model Doesn’t work generally. Only works for hydrogen atoms (and other monoelectronic species). Electrons do not move in circles . The energy quantization is right, but not because they are circling like planets. So, we need another model (LD 4.12)

55. 7.5 The Quantum Mechanical Model A totally new approach. De Broglie said matter could be like a wave. De Broglie said they were like standing waves. The vibrations of a stringed instrument.

57. Standing Waves - fixed or “quantized” wavelengths, d = n (  /2) nodes d = (1/2)  d =  d = (3/2) 

58. Figure 7.9 The Standing Waves Caused by the Vibration of a Guitar String Fastened at Both Ends. Each dot represents a node (a point of zero displacement).

59. What’s possible? You can only have a standing wave if you have complete waves (standing wave generator demo). There are only certain allowed waves. In the atom there are certain allowed waves called electrons. 1925 Erwin Schrödinger described the wave function of the electron. Much math but what is important are the solutions.

60. Figure 7.10 The Hydrogen Electron Visualized as a Standing Wave Around the Nucleus Destructive interference occurs if orbit does not equal a complete wave. So only certain electron energies are allowed.

61. “ allowed” orbit = constructive interference “ forbidden” orbit = destructive interference Standing Waves Quantum Mechanics E. Schrödinger (1927)

62. The Schrodinger Wave Equation Energy is quantized . It comes in chunks. A quanta is the amount of energy needed to move from one energy level to another . Since the energy of an atom is never “in-between” there must be a quantum leap in energy. Schrodinger derived an equation that described the energy and probable position of the electrons in an atom.

63. Schrödinger’s Equation The wave function is a F(x, y, z) Solutions to the equation are called orbitals . These are not Bohr orbits. Each solution is tied to a certain energy. These are the energy levels .

64. There is a limit to what we can know We can’t know how the electron is moving or how it gets from one energy level to another. The Heisenberg Uncertainty Principle. There is a limit to how well we can know both the position and the momentum of an object.

65. Heisenberg Uncertainty Principle It is impossible to know exactly the position and velocity of a particle at the same time . The better we know one, the less we know the other. The act of measuring changes the properties.

66. More obvious with the very small To measure where a electron is, we use light. But the light moves the electron And hitting the electron changes the frequency of the light . Both the electron and the light are changed by the collision. Light photons are too small to affect anything other than electrons in the manner.

67. Moving Electron Photon Before Electron Changes velocity Photon changes wavelength After

68. Mathematically  x ·  (mv) > h/4   x is the uncertainty in the position.  (mv) is the uncertainty in the momentum. the minimum uncertainty is h/4 

69. Heisenberg's Uncertainty Principle We can never SIMULTANEOUSLY know with absolute precision both the exact position (x), and momentum (mass X velocity or mv), of the electron. If one uncertainty gets very small, then the other becomes very large  x •  (mv) > h Uncertainty in momentum Uncertainty in position Planck’s constant

70. If an electron is moving at 1.0 X 10 8 m/s with an uncertainty in velocity of 0.10 %, then what is the uncertainty in position?  x •  (mv) > h and rearranging  x > h /  (mv) or since the mass is fixed  x > h / m  v  x > 7.3 X 10 -9 m or 7300 pm  x > (6.63 X 10 -34 Js) (9.11 X 10 -31 kg)(.001 X 1 X 10 8 m/s)

71. Examples - Plug & Chug We’ll skip the problems, know the concept What is the uncertainty in the position of an electron. mass 9.31 x 10 - 31 kg with an uncertainty in the speed of .100 m/s What is the uncertainty in the position of a baseball, mass .145 kg with an uncertainty in the speed of .100 m/s

72. What does the wave Function mean? Nothing. It is not possible to visually map it. The square of the function is the probability of finding an electron near a particular spot. Best way to visualize it is by mapping the places where the electron is likely to be found.

73. Probability Distance from nucleus

74. Sum of all Probabilities Distance from nucleus

75. Defining the size The nodal surface. The size that encloses 90% to the total electron probability. NOT at a certain distance, but a most likely distance. For the first solution it is a sphere.

76. We can construct atomic orbitals by drawing a boundary at the place where probability = 90%

77. Note on online HW pp #6 is correct - check your units!. When a question asks, “how much heat is liberated ,” your answer will be positive because there is no “negative” heat. When a question asks, “what is the change in heat” then you have to indicate the change by a (+) or (-) sign. When you use energy or heat in a mathematical equation (e.g., q = m∆TC p then you also have to show the sign.

78. 7.6 Quantum Numbers There are many solutions to Schrödinger’s equation Each solution can be described with 4 quantum numbers (n, l, m, s) that describe some aspect of the solution. Analogous to y = mx + b describing a line (4 variables).

79. Atomic Orbitals & Quantum Numbers Principal Quantum Number ( n ) = the main energy level of the electron. Tells us the size (distance from the nucleus) and energy of an orbital. Has integer values of n = 1, 2, 3, . . .

80. Angular Momentum Quantum Number (l) Within each energy level the complex math of Schrodinger’s equation describes several shapes ( l ). These shapes are called atomic orbitals They are regions where there is a high probability of finding an electron.

81. The 2nd quantum number Angular momentum quantum number l . Describes the shape of the orbital. Has integer values from 0 to n-1 l = 0 is called s and has shape of? l = 1 is called p l = 2 is called d l = 3 is called f l = 4 is called g

82. 3rd Quantum number (m) Magnetic quantum number (m l ) Has integer values between - l and + l Tells orientation of each shape.

83. S orbitals

84. "s" Atomic Orbitals 1s 2s 3s Orbitals are found in 3-D shells instead of 2-D Bohr orbits. The Bohr radius for n=1 was correct, however. + n = 1 n = 2 n = 3

86. P orbitals

87. "p" Atomic Orbitals “ p” orbitals only exist in the 2nd shell and higher (n = 2, 3, ...) + n = 1 n = 2 n = 3 3p x 3p y 3p z 2p x 2p y 2p z

89. P Orbitals

90. D orbitals

91. "d" Atomic Orbitals “ d” orbitals only exist for n = 3, 4, 5…. + n = 1 n = 2 n = 3 3d z 2 3d xz 3d yz 3d xy 3d x2-y2

92. Three F orbitals

93. Other four F orbitals

94. "f" Atomic Orbitals Do not appear until the 4th shell and higher

95. “ The Shell Game” (n = 1) n = 1 n = 2 n = 3 +

96. “ The Shell Game” n = 2 + n = 1 n = 2 n = 3

97. “ The Shell Game” n = 3 + n = 1 n = 2 n = 3

98. pp

99. pp

100. Go to application, Atom in a Box pp

101. Quantum Numbers n = # of sublevels per level n 2 = # of orbitals per level Sublevel sets: 1 s, 3 p, 5 d, 7 f

102. 7.8 Electron Spin & the Pauli Principle 4th Quantum number (s) Electron spin quantum number (either symbolized as “s” or as “ m s ”) Can have 2 values only. Either +1/2 or -1/2 LD 1: 4.30 & 4.31 Electron Spin

103. Figure 7.19 A Picture of the Spinning Electron

104. Pauli Exclusion Principle No two electrons in the same atom can have the same set of 4 quantum numbers. This means . . . At most 2 electrons per orbital - each with different spins

105. 7.9 Polyelectronic Atoms More than one electron. Three energy contributions. The kinetic energy of moving electrons. The potential energy of the attraction between the nucleus and the electrons. The potential energy from repulsion of electrons.

106. Polyelectronic atoms Can’t solve Schrödinger's equation exactly. Difficulty is repulsion of other electrons. Solution is to treat each electron as if it were affected by the net field of charge from the attraction of the nucleus and the repulsion of the electrons. Effective nuclear charge

107. +11P 11 electrons +11P 10 other electrons e - Z eff

108. Effective Nuclear charge Can be calculated from E = -2.178 x 10 -18 J (Z eff 2 / n 2 ) and  E = -2.178 x 10 -18 J Z eff 2 (1/ n f 2 - 1/ n i 2 )

109. Summary: Polyelectronic Effect In a hydrogen atom there is only one electron. So, its energy sublevels (orbitals) are equal (because no interference from other electrons).

110. Figure 7.18 Orbital Energy Levels for the Hydrogen Atom (degenerate)

111. Figure 7.18 Orbital Energy Levels for the H Atom (degenerate)

112. Summary continued But, in a polyelectronic orbital the sublevels are not equal in energy. Electrons “prefer” the order s, p, d, f . E.g., the 2s electron “penetrates” to the nucleus more than the 2p e - . So, the 2s orbital is lower in energy. Penetration effects produces the Aufbau principle (arrow diagram)

113. Increasing energy 1s 2s 3s 4s 5s 6s 7s 2p 3p 4p 5p 6p 3d 4d 5d 7p 6d 4f 5f

114. 7.10 The History of the Periodic Table Developed independently by German Julius Lothar Meyer and Russian Dmitri Mendeleev (1870”s). Didn’t know much about the atom. Put in columns by similar properties. Predicted properties of missing elements.

115. History of the Periodic Table Russian scientist, Dmitri Mendeleev, taught chemistry in terms of properties. Mid 1800 - molar masses of elements were known. He wrote down the elements in order of increasing atomic mass . He found a pattern of repeating properties .

116. Mendeleev’s Table Grouped elements in columns by similar properties in order of increasing atomic mass . Found some inconsistencies - felt that the properties were more important than the mass, so switched order for some. He found some gaps . He concluded . . . Must be undiscovered elements. Predicted their properties before they were found. (Sc, Ga, Ge)

117. Mendeleev’s Early Periodic Table, Published in 1872 Note the spaces left for missing elements with atomic masses 44, 68, 72 and 100.

118. Mendeleev’s Table Two questions remained: Why can most elements be arranged in order of atomic mass , but a few can’t ? What was the reason for chemical periodicity? Mosely : found the patterns fit better when arranged in order of nuclear charge (the atomic number vs . mass).

119. The modern table The Periodic Law : physical & chemical properties of the elements are periodic functions of their atomic numbers . The Periodic Table : Arranges elements in order of increasing atomic number (not mass), so elements with similar properties are in the same group (column). Let’s look at an example of this . . .

120. Modern PT by atomic # (& properties) Compare Sb, Te, I (look at your PT) 53 52 51 Atomic # I Te Sb Symbol 126.90 127.60 121.75 Mass # Iodine Tellurium Antimony Name 17 16 15 Gp #  (Per. 5)

121. The Modern Table Elements still grouped by properties . Similar properties in the same column . Order is in increasing atomic number . Added a column of elements Mendeleev didn’t know about (noble gases). The noble gases weren’t found because they didn’t react with anything . Last column on the Periodic Table Also added lanthanides & actinides .

122. 7.11 The Aufbau Principle & the Periodic Table Aufbau is German for building up. As the protons are added one by one, the electrons fill up hydrogen-like orbitals. Fill up in order of energy levels. This causes difficulties because of the overlap of orbitals of different energies.

123. He with 2 electrons Increasing energy 1s 2s 3s 4s 5s 6s 7s 2p 3p 4p 5p 6p 3d 4d 5d 7p 6d 4f 5f

124. Hund’s Rule When electrons occupy orbitals of equal energy they do not pair up until they have to. (Each gets its own room) Let’s determine the electron configuration for Phosphorus Need to account for 15 electrons (same as atomic number)

125. The first two electrons go into the 1s orbital Notice the opposite spins only 13 more to go Increasing energy 1s 2s 3s 4s 5s 6s 7s 2p 3p 4p 5p 6p 3d 4d 5d 7p 6d 4f 5f

126. The next electrons go into the 2s orbital only 11 more Increasing energy 1s 2s 3s 4s 5s 6s 7s 2p 3p 4p 5p 6p 3d 4d 5d 7p 6d 4f 5f

127. The next electrons go into the 2p orbital only 5 more Increasing energy 1s 2s 3s 4s 5s 6s 7s 2p 3p 4p 5p 6p 3d 4d 5d 7p 6d 4f 5f

128. The next electrons go into the 3s orbital only 3 more Increasing energy 1s 2s 3s 4s 5s 6s 7s 2p 3p 4p 5p 6p 3d 4d 5d 7p 6d 4f 5f

129. The last three electrons go into the 3p orbitals. They each go into separate shapes 3 unpaired electrons 1s 2 2s 2 2p 6 3s 2 3p 3 Increasing energy 1s 2s 3s 4s 5s 6s 7s 2p 3p 4p 5p 6p 3d 4d 5d 7p 6d 4f 5f

130. Orbital Diagrams Use individual orbitals Give subshell arrangement Each orbital takes one electron before any other orbital in the same subshell can receive a second electron

131. Orbital Diagram for A Nitrogen Atom N 1s 2s 2p 3s     

132. Orbital Diagram for A Fluorine Atom F 1s 2s 2p 3s     

133. Orbital Diagram for A Magnesium Atom Mg 1s 2s 2p 3s      

134. Learning Check O1 Write the orbital diagram for the electrons in an oxygen atom. . . Ans.

135. Solution O1 Write the orbital diagram for the electrons in an oxygen atom. 1s 2s 2p 3s     

136. Tr23 Aufbau Principle What is the maximum electrons in each box? Two Which is a higher energy level, 4d or 5s? 4d Which is farther from the nucleus, 4d or 5s? 5s

137. Details Valence electrons - s & p electrons in the outermost energy sublevels (not d). Core electrons - the inner electrons. Hund’s Rule - The lowest energy configuration for an atom is the one having the maximum number of unpaired electrons in the orbital . C 1s 2 2s 2 2p 2

138. Fill from the bottom up following the arrows 1s 2 2 electrons 2s 2 4 2p 6 3s 2 12 3p 6 4s 2 20 3d 10 4p 6 5s 2 38 4d 10 5p 6 6s 2 56 1s 2s 2p 3s 3p 3d 4s 4p 4d 4f 5s 5p 5d 5f 6s 6p 6d 6f 7s 7p 7d 7f

139. Details Elements in the same column have the same outer electron configuration . Put in columns because of similar properties . Similar properties because of electron configuration. Noble gases have filled energy levels. Transition metals are filling the d orbitals

140. Sublevel Blocks s 1 s 2 p 1 p 2 p 3 p 4 p 5 p 6 1 2 3 d 1 - d 10 4 5 6 f 1 - f 14

141. The “Extended” Periodic Table pp

142. 1 s 1 1s 2 2 s 1 1s 2 2s 2 2p 6 3 s 1 1s 2 2s 2 2p 6 3s 2 3p 6 4 s 1 1s 2 2s 2 2p 6 3s 2 3p 6 4s 2 3d 10 4p 6 5 s 1 1s 2 2s 2 2p 6 3s 2 3p 6 4s 2 3d 10 4p 6 5s 2 4d 10 5p 6 6 s 1 1s 2 2s 2 2p 6 3s 2 3p 6 4s 2 3d 10 4p 6 5s 2 4d 10 5p 6 6s 2 4f 14 5d 10 6p 6 7 s 1 H 1 Li 3 Na 11 K 19 Rb 37 Cs 55 Fr 87

143. 1 s 2 1s 2 2s 2 2p 6 1s 2 2s 2 2p 6 3s 2 3p 6 1s 2 2s 2 2p 6 3s 2 3p 6 4s 2 3d 10 4p 6 1s 2 2s 2 2p 6 3s 2 3p 6 4s 2 3d 10 4p 6 5s 2 4d 10 5p 6 1s 2 2s 2 2p 6 3s 2 3p 6 4s 2 3d 10 4p 6 5s 2 4d 10 5p 6 6s 2 4f 14 5d 10 6p 6 He 2 Ne 10 Ar 18 Kr 36 Xe 54 Rn 86

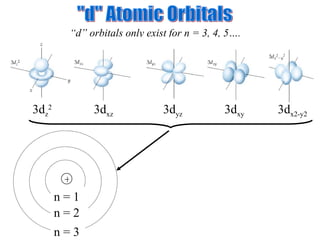
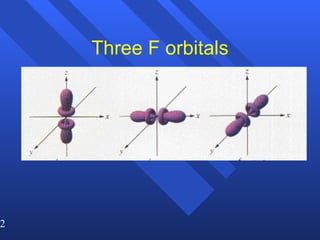
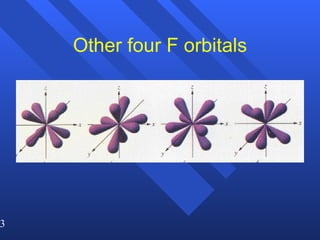
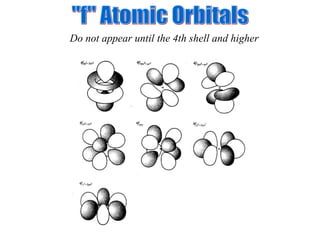
144. Exceptions Ti = [Ar] 4s 2 3d 2 V = [Ar] 4s 2 3d 3 Cr = [Ar] 4s 1 3d 5 Mn = [Ar] 4s 2 3d 5 Half filled orbitals (only with d-orbitals). Scientists aren’t sure of why it happens. same for Cu [Ar] 4s 1 3d 10

145. Aufbau Web Graphic http://intro.chem.okstate.edu/WorkshopFolder/Electronconfnew.html

146. More exceptions Lanthanum La: [Xe] 6s 2 5d 1 Cerium Ce: [Xe] 6s 2 4f 1 5d 1 Promethium Pr: [Xe] 6s 2 4f 3 5d 0 Gadolinium Gd: [Xe] 6s 2 4f 7 5d 1 Lutetium Pr: [Xe] 6s 2 4f 14 5d 1 Then we go back to Aufbau filling: Hafnium Hf: [Xe] 6s 2 4f 14 5d 2 We’ll just pretend that all except Cu and Cr follow the rules.

147. A Quick Detour The concept of shielding and penetration of electrons in orbitals. Catch the concepts, don’t worry too much about the math. Some AP questions. This detour includes next 18 slides.

148. More Polyelectronic We can use Z eff to predict properties , if we determine its pattern on the periodic table. Can use the amount of energy it takes to remove an electron for this. Ionization Energy - The energy necessary to remove an electron from a gaseous atom.

149. Remember this? E = -2.18 x 10 -18 J(Z 2 /n 2 ) was true for Bohr atom. Can be derived from quantum mechanical model as well For a mole of electrons being removed (so use positive value for E). E =(6.02 x 10 23 /mol)2.18 x 10 -18 J(Z 2 /n 2 ) E = 1.31 x 10 6 J/mol(Z 2 /n 2 ) E = 1310 kJ/mol(Z 2 /n 2 )

150. Example Calculate the ionization energy of B +4 E = 1310 kJ/mol(Z 2 /n 2 ) 1310(5 2 )/1 2 n= 1 because the remaining 1s e- is being removed) = 32 750 kJ/mol

151. Remember our simplified atom +11 11 e- Z eff 1 e-

152. This gives us Ionization energy = 1310 kJ/mol(Z eff 2 /n 2 ) So we can measure Z eff The ionization energy for a 1s electron from sodium is 1.39 x 10 5 kJ/mol . The ionization energy for a 3s electron from sodium is 4.95 x 10 2 kJ/mol . Demonstrates shielding.

153. Shielding The electron on the outside energy level has to look through all the other energy levels to see the nucleus.

154. Shielding So, it is less affected by the nucleus. So, lower effective nuclear charge on it (blocking by the inner electrons) And easier to be removed. So, lower IE

155. Shielding Electrons on the higher energy levels tend to be farther out . Have to look through the other electrons to see the nucleus. So, less affected by the nucleus. Lower effective nuclear charge on them If shielding were completely effective, Z eff = 1 ( e.g ., in Na, 10 p + cancel 10 e - leaving the 11th p + to have a Z effect on the 11th e - Why isn’t the shielding complete?

156. Penetration There are levels to the electron distribution for each orbital. 2s

157. Graphically Penetration 2s Radial Probability Distance from nucleus

158. Graphically Radial Probability Distance from nucleus 3s

159. Radial Probability Distance from nucleus 3p

160. Radial Probability Distance from nucleus 3d

161. Radial Probability Distance from nucleus 4s 3d

162. Penetration effect The outer energy levels penetrate the inner levels so the shielding of the core electrons is not totally effective. From most penetration to least penetration the order is ns > np > nd > nf (within the same energy level). This is what gives us our order of filling, electrons prefer s and p.

163. How orbitals differ The more positive the nucleus, the smaller the orbital. A sodium 1s orbital is the same shape as a hydrogen 1s orbital, but it is smaller because the electron is more strongly attracted to the nucleus (11 P + vs. 1 P + ). The helium 1s is smaller than H’s 1s also. This provides for better shielding.

164. Z eff 1 2 4 5 1

165. Z eff 1 2 4 5 1 If shielding is perfect Z= 1

166. Z eff 1 2 4 5 1 No shielding Z = Z eff

167. Z eff 1 2 4 5 16

168. Back To Basics Now Let’s look at periodic trends.

169. 7.12 Periodic Trends in Atomic Properties Ionization energy is the energy required to remove an electron from a gaseous atom. X (g) + energy  X + (g) + e - Highest energy electron removed first . First ionization energy ( I 1 ) is that required to remove the first electron. Second ionization energy ( I 2 ) - the second electron etc. etc.

170. Trends in ionization energy for Mg I 1 = 735 kJ/mole I 2 = 1445 kJ/mole I 3 = 7730 kJ/mole The effective nuclear charge increases as you remove electrons. Notice the big jump between I 2 and I 3. It takes much more energy to remove a core electron than a valence electron because there is less shielding.

171. Symbol First Second Third HHeLiBeBCNO F Ne 1312 2731 520 900 800 1086 1402 1314 1681 2080 5247 7297 1757 2430 2352 2857 3391 3375 3963 11810 14840 3569 4619 4577 5301 6045 6276

172. Symbol First Second Third HHeLiBeBCNO F Ne 1312 2731 520 900 800 1086 1402 1314 1681 2080 5247 7297 1757 2430 2352 2857 3391 3375 3963 11810 14840 3569 4619 4577 5301 6045 6276 Why such increase between the arrows? Special stability of noble gas configuration makes it harder to remove an inner shell electron

173. Summary of Noble Gas Configuration effects on IE

174. Explain this trend For Al I 1 = 580 kJ/mole I 2 = 1815 kJ/mole I 3 = 2740 kJ/mole I 4 = 11,600 kJ/mole Answer . . . I 4 represents removing a core e-

175. Across a Period & Down a Group Generally from left to right, I 1 increases because . . . There is a greater nuclear charge with the same shielding . As you go down a group I 1 decreases because . . . Electrons are farther away.

176. Sample FR Problem Given 3 different atoms 1s 2 2s 2 2p 6 1s 2 2s 2 2p 6 3s 1 1s 2 2s 2 2p 6 3s 2 Which has largest I 1 ? . . . 1s 2 2s 2 2p 6 (Ne) - found at right end of PT ; also, 2p electrons not effective shielders and the other two choices have 3s electrons, which are effectively shielded by the core electrons and farther from the nucleus.

177. Sample FR Problem Given 3 different atoms 1s 2 2s 2 2p 6 1s 2 2s 2 2p 6 3s 1 1s 2 2s 2 2p 6 3s 2 Which has smallest I 2 ? . . . 1s 2 2s 2 2p 6 3s 2 (Mg) - both I 1 & I 2 involve valence electrons (s electrons). The Na 1s 2 2s 2 2p 6 3s 1 would lose both a valence and a core electron from a p-orbital (hard to do). The Ne 1s 2 2s 2 2p 6 has ineffective shielding so its IE is relatively large.

178. It is not that simple, though Z eff changes as you go across a period, so will I 1 . Half filled and filled orbitals are harder to remove electrons from. So those have higher I 1 energies. Here’s what it looks like.

179. He has a greater IE than H because . . . same shielding (same level) but . . . greater nuclear charge . Always ask yourself about shielding and nuclear charge First Ionization energy Atomic number He H

180. First Ionization energy Atomic number H He Li has lower IE than H More shielding because . . . Further away This outweighs greater nuclear charge Li

181. First Ionization energy Atomic number H He Be has higher IE than Li same shielding (same row) greater nuclear charge (further away) Li Be

182. First Ionization energy Atomic number H He B has lower IE than Be same shielding (row) greater nuclear charge but By removing an electron we make s orbital filled , which itself has lower energy so easier to remove and lower IE. Li Be B

183. First Ionization energy Atomic number H He Li Be B C

184. First Ionization energy Atomic number H He Li Be B C N

185. Oxygen breaks the pattern because removing an electron gets it down to 1/2-filled p sublevel (white board) First Ionization energy Atomic number H He Li Be B C N O

186. First Ionization energy Atomic number H He Li Be B C N O F

187. Ne has a lower IE than He. Why?. . . Both are full, but… Ne has more shielding because Greater distance Always compare shielding to distance. First Ionization energy Atomic number H He Li Be B C N O F Ne

188. First Ionization energy Atomic number H He Li Be B C N O F Ne Na has a lower IE than Li. Why? Both are s 1 but Na has more shielding because Greater distance (4th level) Na

189. First Ionization energy Atomic number

190. Tr22A Summary of the previous trends

191. Figure 7.31 The Values of First Ionization Energy for the Elements in the First Six Periods

192. Figure 7.32 Trends in Ionization Energies for the Representative Elements

193. Electron Affinity The energy change associated with adding an electron to a gaseous atom Opposite to IE (which is energy for losing an electron. A + energy  A + + e - ) Has negative value (since energy is lost ) A + e -  A - + energy Easiest to add e - s to group 17 (why?). Gets to full energy level (noble gas). LD 1: 5.32 Electron affinity of Chlorine

194. Electron Affinity Trends Period (row) Trends Increases from left to right because atoms get smaller , with greater nuclear charge . Group (column) Trends Decreases as we go down a group (i.e ., harder to add an e - (shielding from nucleus) Adding electrons to (-) ions Always more difficult to add another e - to an already (-) charged ion, so these affinities have (+) values.

195. Electron Affinity Trends Adding electrons to negative ions Always more difficult to add another e - to an already (-) charged ion, so these affinities have (+) values.

196. Table 5.17 p. 147 Observe period and group trends

197. Atomic Size First problem: Where do you start measuring . The electron cloud does not have a definite edge. We get around this by measuring more than 1 atom at a time as follows . . .

198. Atomic Size Atomic Radius = half the distance between two nuclei of a diatomic molecule LD 1:5.22 Radius of Chlorine. } Radius

199. Trends in Atomic Size Influenced by two factors: Energy Level . . . Higher energy level is further away. Charge on the nucleus More charge pulls electrons in closer . These are competing factors .

200. Periodic Trends Going across a period the radius gets smaller because . . . Same energy level (same distance from nucleus), but . . . More nuclear charge . So, outermost electrons are closer . Na Mg Al Si P S Cl Ar

201. Group trends As we go down a group Each atom has another energy level So the atoms get bigger (with some exceptions). H Li Na K Rb

202. Atomic Radii for Selected Atoms Why is Ga smaller than Al? Gallium, unlike Al, is preceded by 10 d-block elements The expected increase in radius caused by filling the 4th level is outweighed by a shrinking of electron cloud caused by Ga’s nuclear charge that is considerably larger (31 vs. 13) than for Al. Compare Ga & Al on next slide (showing d-block)

203. Tr 26 Fig. 5.13 p. 141 Atomic Radii Mg to Al size gets smaller because same level with more p + s Zn to Ga size jumps because of electron shielding from the d-electrons that makes the increasing nuclear charge less effective, so the electron cloud gets larger.

204. Overall Atomic Number Atomic Radius (nm) H Li Ne Ar 10 Na K Kr Rb

205. Tr21A Fig 5.14 p 142 Atomic Radius vs Atomic Number How does “effective” nuclear charge change left to right Increases Why is there a “peak” in Period 4? Inner 3d sublevel has filled & now in outer 4p sublevel Why is there a U-shape curve across Period 5? As add more 4d electrons, the shielding effect overcomes the effective nuclear charge.

206. Parts of the Periodic Table

207. The information it hides Know the special groups. It is the number and type of valence electrons that determine an atom’s chemistry . You can get the electron configuration from the periodic table. Metals lose electrons and have the lowest IE Nonmetals - gain electrons and have the most negative electron affinities.

208. The Properties of a Group: The Alkali Metals Doesn’t include hydrogen - behaves as a nonmetal. Going down, get: Decrease in IE increase in radius Decrease in density decrease in melting point Behave as reducing agents

209. Reducing ability Lower IE = better reducing agents. Cs > Rb > K > Na > Li in reducing ability Works for solids , but not in aqueous solutions. Get opposite effect. In solution Li > K > Na Why? It’s the water - there is an energy change associated with dissolving.

210. Hydration Energy It is exothermic for Li + = -510 kJ/mol for Na + = -402 kJ/mol for K + = -314 kJ/mol Li’s is so big because it has a high charge density; i.e., a lot of charge on a small atom. Li loses its electron more easily because of this in aqueous solutions

211. The reaction with water Na and K react explosively with water. Li doesn’t. LD 1: 5.8, 5.10, 5.11, braniacs Even though Li’s reaction has a more negative  H than that of Na and K. Na and K melt.  H does not tell you speed of reaction More about that in Chapter 12.

212. Periodic (row) Trend Metals are at the left end. They let their electrons go easily So, have low electronegativity At the right end are the nonmetals . They want more electrons. Try to take them away from their playmates. So, have high electronegativity.

213. Group (column) Trend The further down a group the farther the electron is away and the more electrons an atom has (and more shielding). More willing to share with another since the nucleus doesn’t hold on to the outer electrons so tightly (shielding). So, low electronegativity.

214. Ionization energy, Electronegativity, Electron affinity INCREASE

215. Ionization energy, Electronegativity Electron affinity INCREASE

216. Atomic size increases, (shielding constant across a period) Ionic size increases

217. Atomic size increases, (shielding constant across a period) Ionic size increases

218. The Big Review Given 5 elements E : 2s 2 2p 5 G : 4d 10 5s 2 5p 5 J : 2s 2 2p 2 L : 5d 10 6s 2 6p 5 M: 2s 2 2p 4 ID block location (without PT) . All are in p-block Which in same period? EJM same period (2nd) Same group? EGL same group (17)

219. The Big Review Given 5 elements E : 2s 2 2p 5 G : 4d 10 5s 2 5p 5 J : 2s 2 2p 2 L : 5d 10 6s 2 6p 5 M: 2s 2 2p 4 Which has highest e - affinity? E Forms 1 - ion? EGL form 1 minus ions. Highest electronegativity? E (closest to upper right of PT)

220. The Big Review Given 5 elements E : 2s 2 2p 5 G : 4d 10 5s 2 5p 5 J : 2s 2 2p 2 L : 5d 10 6s 2 6p 5 M: 2s 2 2p 4 Which is larger, G or G ion? G ion (-). Added electron, cloud is bigger Which contain(s) 7 valence e - ? EGL (all have s 2 p 5 outer electrons)