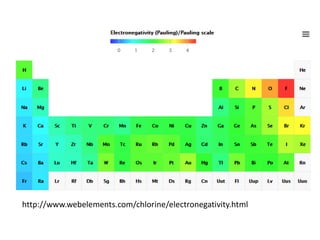
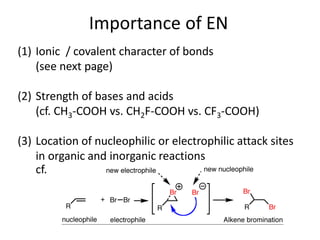
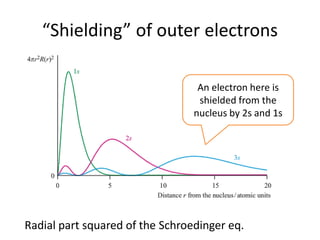
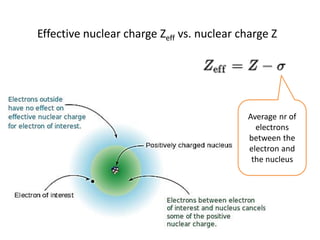
This document discusses atomic structure and electron configuration. It begins by explaining Slater's rules for calculating effective nuclear charge. It then provides examples of applying Slater's rules to determine electron shielding and effective nuclear charge. The document also covers electron configurations, term symbols, Hund's rules, and periodic trends in atomic size, ionization energy, and metallic character across periods and groups. It defines concepts like ionization potential, electron affinity, and electronegativity scales. In summary, the document provides an in-depth overview of theoretical atomic structure concepts.

1. Atomic Structure Part 3
Dr. Chris
UP Aug.2016

2. SLATER RULES TO CALCULATE
EFFECTIVE CHARGE

3. “Shielding” of outer electrons
Radial part squared of the Schroedinger eq.
An electron here is
shielded from the
nucleus by 2s and 1s

4. Effective nuclear charge Zeff vs. nuclear charge Z
Average nr of
electrons
between the
electron and
the nucleus

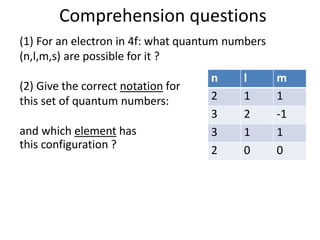
5. Slater’s rule
Group el. in the
same
group
el. in same
shell n and
orbital nr < l
el. in shell
n-1
el. in shell
< n-2
[ 1s] 0.30 - - -
[ns np ] 0.35 - 0.85 1
[nd] or [nf] 0.35 1 1 1

6. Examples
Fe atom which has nuclear charge 26 and
electronic configuration 1s22s22p63s23p63d64s2

7. http://www.wikihow.com/Determine-Screening-
Constant-and-Effective-Nuclear-Charge

9. Example V vs. V2+
Configuration for V:
In V2+ : the 2 4s electrons or 2 3d electrons missing ?
-> We estimate the effective nuclear charge that acts
on the 4s vs. 3d electrons

10. Solution
Configuration V: (1s) (2s 2p) (3s 3p) (3d) (4s 4p)
[Ar] 4s2 3d3
Shielding for one 4s electron: S = 10 + 11 * 0.85 + 0.35
Z* = 3.30
Shielding for one 3d electron: S = 18 + 2 * 0.35
Z* = 4.30
=> The 4s electrons are less attracted than 3d

11. Effect on atomic radii

13. Irregularity: Zn -> Ga
Shielding of 3d10 in Zn:
(1s)(2s 2p)(3s 3p)(3d)(4s 4p)(4d)
10 el 8el 10el 2el => S= 18+ 9*0.35
S = 21.15 => Z* = 8.85
Compare with 4p1 of Ga:
(1s)(2s 2p)(3s 3p)(3d)(4s 4p)(4d)
10 el 18el 2el 1el => S= 10 + 18*0.85 + 2*0.35
=> S = 26 => Z* = 5.0

14. Recalling: Uncertainty principle
Assume an electron moves in an H-atom with
diameter of 2 * Bohr Radius = 2 * 0.529 A
= 2 * 0.529 10-10 m = 1.058 10-10 m = ∆x
What is the uncertainty for the speed v ?
(me = 9.1 10-31 kg, h=6.624 10-34 J s)
∆x ∆v m = h/2π

15. TERM SYMBOLS

16. Electronic configuration as “Terms”
Angular momentum L
Is the sum of all individual l of each electron
The angular quantum number l = 0,1,.. (n-1)
Example: n = 2 => l = 0, 1 => s and p
ml = 0
ml = -1 ml = 0 ml = +1
L = -1 + 0 +1 = 0 => Term “S”

17. … and spin multiplicity 2S + 1
The magnetic quantum number can have the values of
- l , - l+1, …. 0, …. l-1, l
Therefore we have 2 l +1 spin states for one l
Example:
S = 3 * ½
= 3/2
-> multiplicity 2S+1 = 4 (“Quartet”)
ml = 0
ml = -1 ml = 0 ml = +1

18. Examples

19. From Shriver/Atkins Chap.20

20. Microstates for 2 el. in a p orbital
5 states belong
to L = 2 (“D”)
9 states belong
to L = 1 (“P”)
1 state with L=0
(“S”)

21. Russell-Saunder Coupling
The angular orbital momentum L couples with spin S
Each state: 2S+1L J is 2*J + 1 degenerated
(same energy)

22. Possible states in np2
L = 2 S= 0 -> J = 2 (2J+1 = 5 x degenerated)
L = 1 S= 1 -> J = 2,1,0 (5x , 3x and 1x = 9 states)
L = 0 S = 0 -> J = 0 (1 state)
Therefore there are 5 electron configurations with
slightly different energies.

23. Which is the ground state ?
Hund’s rules:
1. maximum spin => multiplicity 3 (S = 1)
2. highest L => L = 1 (“P”)
3. Shell < ½ filled -> lowest J
Shell > ½ filled -> highest J
=> 3P0

24. Exercises 1
(1) Order the terms for increasing energy
(2) Find all J-values for each of these 5 states
(3) And find the ground-state

25. Answers

26. http://chemistry.illinoisstate.edu/standard/che362/homework/
362ps11solns.pdf

27. Exercises 2
For a electron configuration 2s1 2p1:
• Determine all possible term symbols
• their degeneracy
• and their energy order

28. Answers 2
The orbital angular momentum is l1=0 and l2=1
The total momentum ranges from |l1-l2| …. l1+l2
-> L = 1 (“P”)
The spin S can be |s1-s2| … s1+s2
-> ½ - ½ = 0 and ½ + ½ = 1
 2 states are possible: 1P and 3P
The total angular momentum J = |L-S| … |L+S|
-> for 1P: (S=0, L=1) J = 1
-> for 3P: (S=1, L=1) J = 2, 1, 0

29. Total number of sub-states:
1P1 -> 2J+1 = 3 states with same energy
3P0 -> 1 state
3P1 -> 3 degenerate states
3P2 -> 5 - “ -

30. Exercises 3

32. Transitions between electronic states
1) Spin – Spin rule:
during a transition the spin S of the system cannot
change: S = 0
2) Laporte Rule:
L = 1 the orbital momentum must change
J = 0 the total momentum cannot change

33. Exercises 4:
electronic transitions
Which transitions are allowed and why :

34. Answers 4

35. ELECTRONIC CONFIGURATION
AND PERIODIC TABLE

36. Electron Configuration and
Periodic Table
Hund’s Rules tell us:
Every orbital in a sublevel is singly occupied
before any orbital is doubly occupied.
All of the electrons in singly occupied orbitals
have the same spin (to maximize total spin).
Pauli Exclusion Principle:
Each electron in an atom must at least have one
different quantum number

37. Hund’s Rules / Pauli principle
Which electron configuration obey both rules ?
1s 2s 2p
1s 2s 2p
1s 2s 2p

38. Periodic Table build up

41. Comprehension questions
(1) For an electron in 4f: what quantum numbers
(n,l,m,s) are possible for it ?
(2) Give the correct notation for
this set of quantum numbers:
and which element has
this configuration ?
n l m
2 1 1
3 2 -1
3 1 1
2 0 0

42. Lanthanoids and Actinoids
(Period 6 and 7)
How many elements are in row 5, 6 and 7 ?
What is the electronic configuration for
Lead, Gold, Cerium, Tungsten, Silver, Mercury,
Americum, Tin, Antimon, Osmium

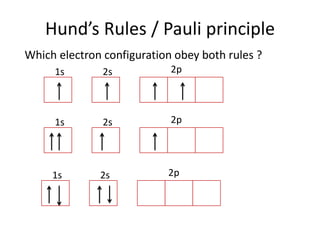
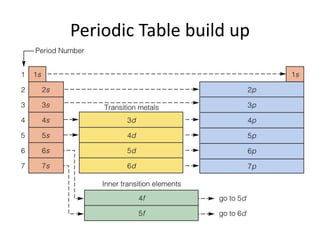
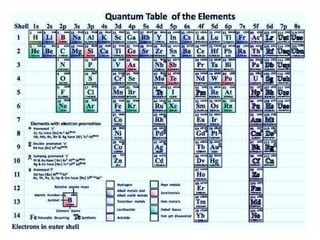
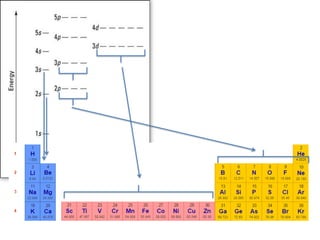
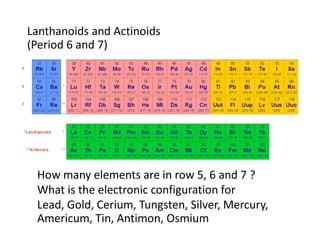
43. Exceptions from Aufbau Principle
La (Z=57) should have configuration:
but has: [Xe] 4f0 5d1 6s2
Ac (Z=89) should have configuration:
but has: [Rn] 5f0 6d1 7s2

44. Exceptions from Hunds’ Rules
Find the electron configuration for:
Cr
Cu
Mo
Pd
Ag
Au

45. Characteristics of Periods
(1) Number of valence electrons increases
(how many VE in the period K -> Kr ?)
(2) Valency towards Hydrogen
Increases from 1 to 4 and back 3 to 1
(write the hydrogen compounds for all elements in period 3)
(3) Size of atoms
(4) Metallic character
(5) Number of shells is the same
(example: how many shells do all elements in period 4 have ?)

46. Characteristics of Groups
(1) Same number of valence electrons
(example: how many VE do all Halogens have ?)
(2) Same valencies
(example: oxygen compounds of group 1, 2 and 4)
(3) Properties of elements
(4) Atomic size increases down
(5) Metallic character increases down
(example: compare Chlorine with Iodine)
(6) Number of electron shells
(example: Li 2,1 (2) Na 2,8,1 (3) K 2,8,8,1 (4) Rb 2,8,18,8,1 (5)

47. Electron Configuration of ions
Find the configuration for:
Cl- 1s2 2s2 2p6
V3+
Fe2+
Br-
S2-
Mn2+
Mn3+
Mn7+

48. ELECTRO NEGATIVITY (EN)

49. Introduced by Pauling 1932
EN values for each element based on the
comparison of bond energies
Arbitrary scale with F as χ = 4 as highest possible
Bond energies cannot always be measured
accurately -> modifications by other scientists

50. http://www.webelements.com/chlorine/electronegativity.html

51. Mulliken EN
Mulliken developed an easier system to calculate EN.
EN is regarded to be the average of
Ionization Potential (IP) and Electron Affinity (EA)
of an element:
χ (A) = IP (A) + EA (A) / 2
To make the values close to Pauling’s EN, a factor of
2.6 is introduced, so that:
χ (A) = IP (A) + EA (A) / (2 * 2.6) = IP (A) + EA (B) / 5.2

52. Example:
Calculate the EN for Fluorine
(IP : 17.4 eV/atom EA: 3.62 eV/atom)

53. Allred – Rochow (AR) EN
They rely on the effective nuclear charge of an element.
The empirical formula is (related to Pauling):
Χ (A) = (Z* e) e / r2 = Z* e2 / r2 => 0.359 Z*/r2 + 0.744
Charge felt
by the VE
Coulomb
attraction
Calculate the EN for Lead: Shielding S is 76.7,
atomic radius 530 pm (Z = 82)
In Angstrom

54. Factors influencing EN
(1) Atomic size
(2) Number of inner shells (=> Z*)
(3) Charge on an ion
(4) Hybridization
(the more s-character, the higher the EN)

55. Importance of EN
(1) Ionic / covalent character of bonds
(see next page)
(2) Strength of bases and acids
(cf. CH3-COOH vs. CH2F-COOH vs. CF3-COOH)
(3) Location of nucleophilic or electrophilic attack sites
in organic and inorganic reactions
cf.

56. Bond characteristics
Linus Pauling suggested an estimation of % ionic character for a
bond:
http://wwwchem.uwimona.edu.jm/courses/CHEM1902/IC10K_MG_Fajans.html