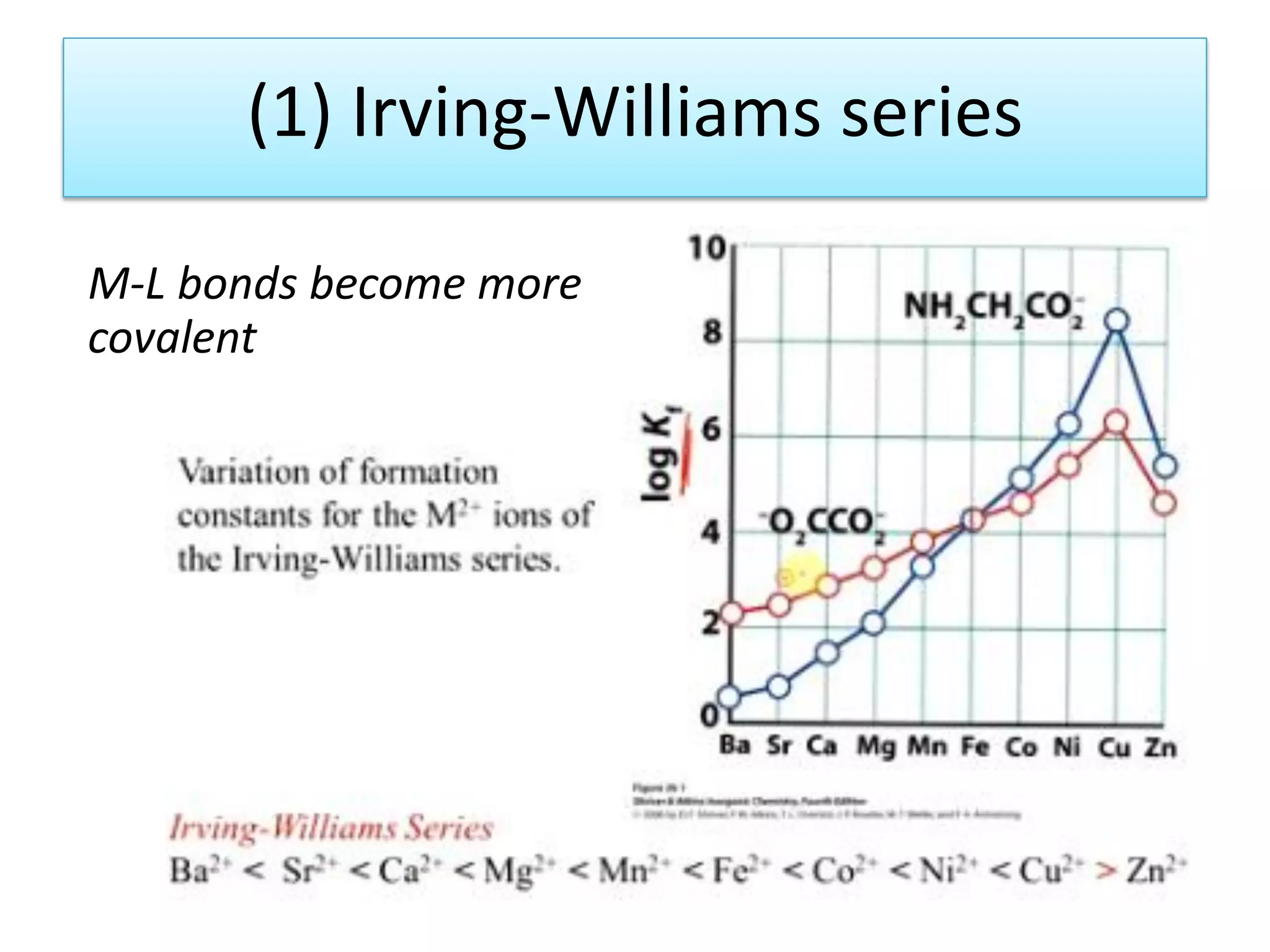
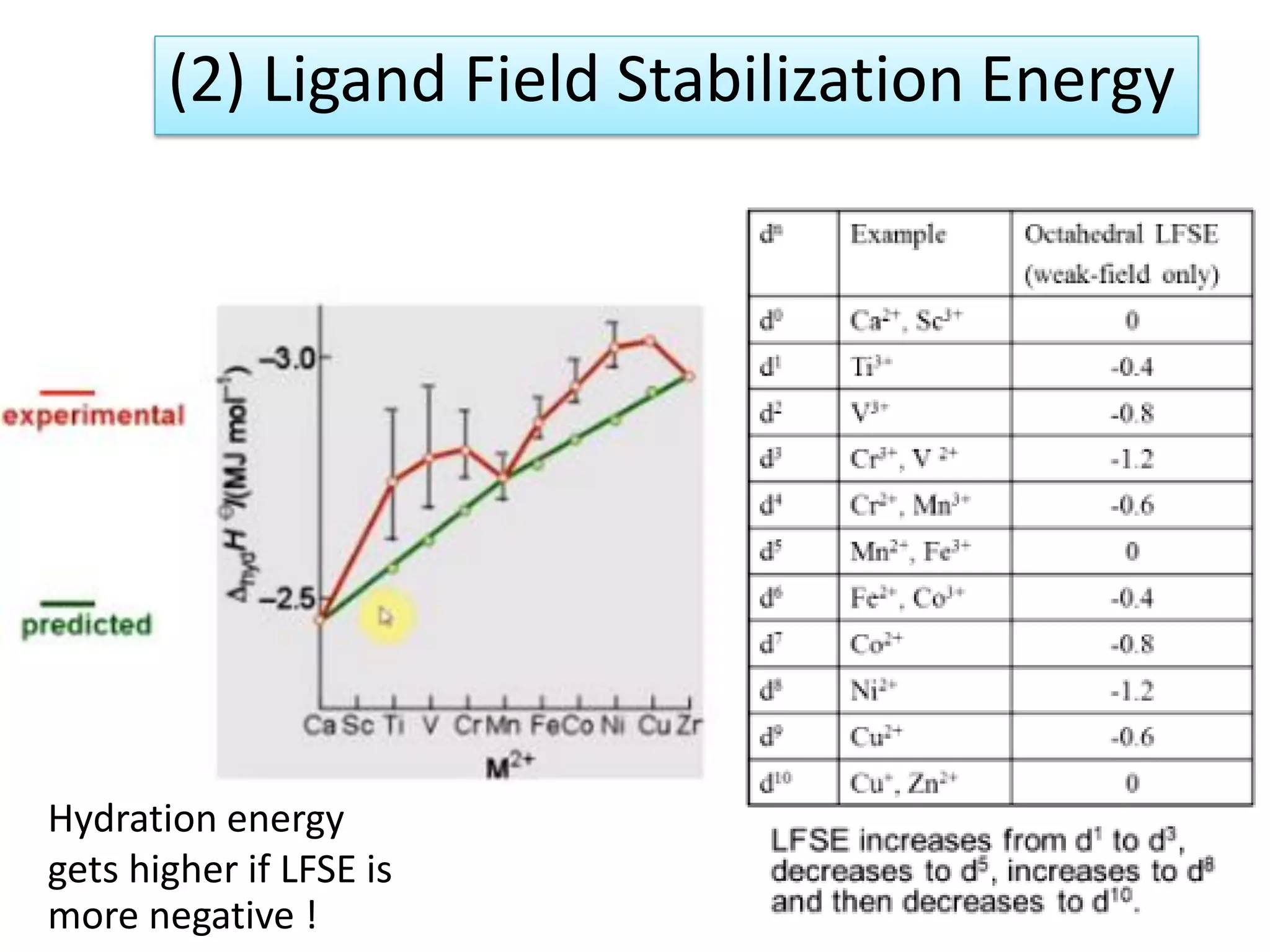
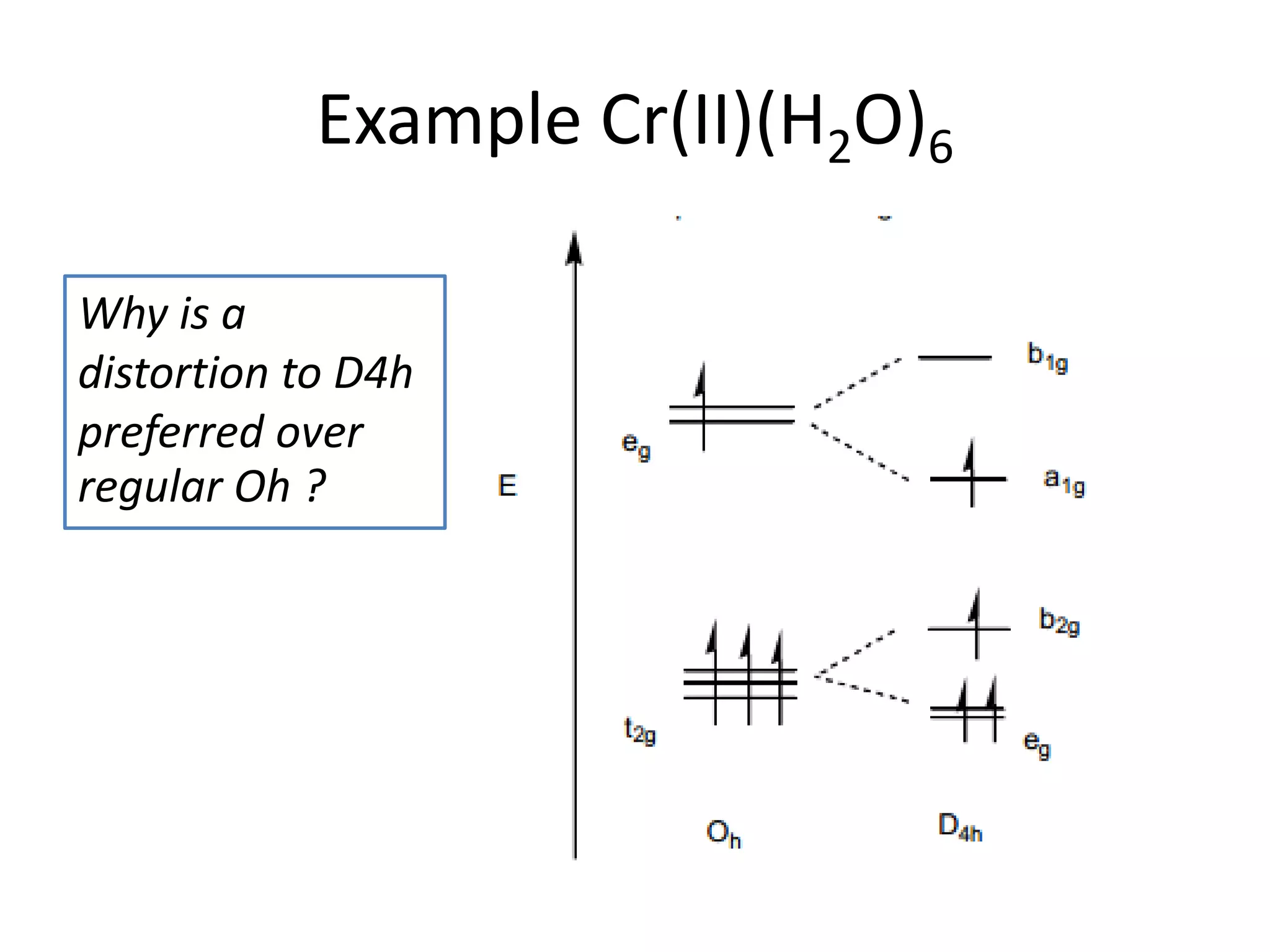
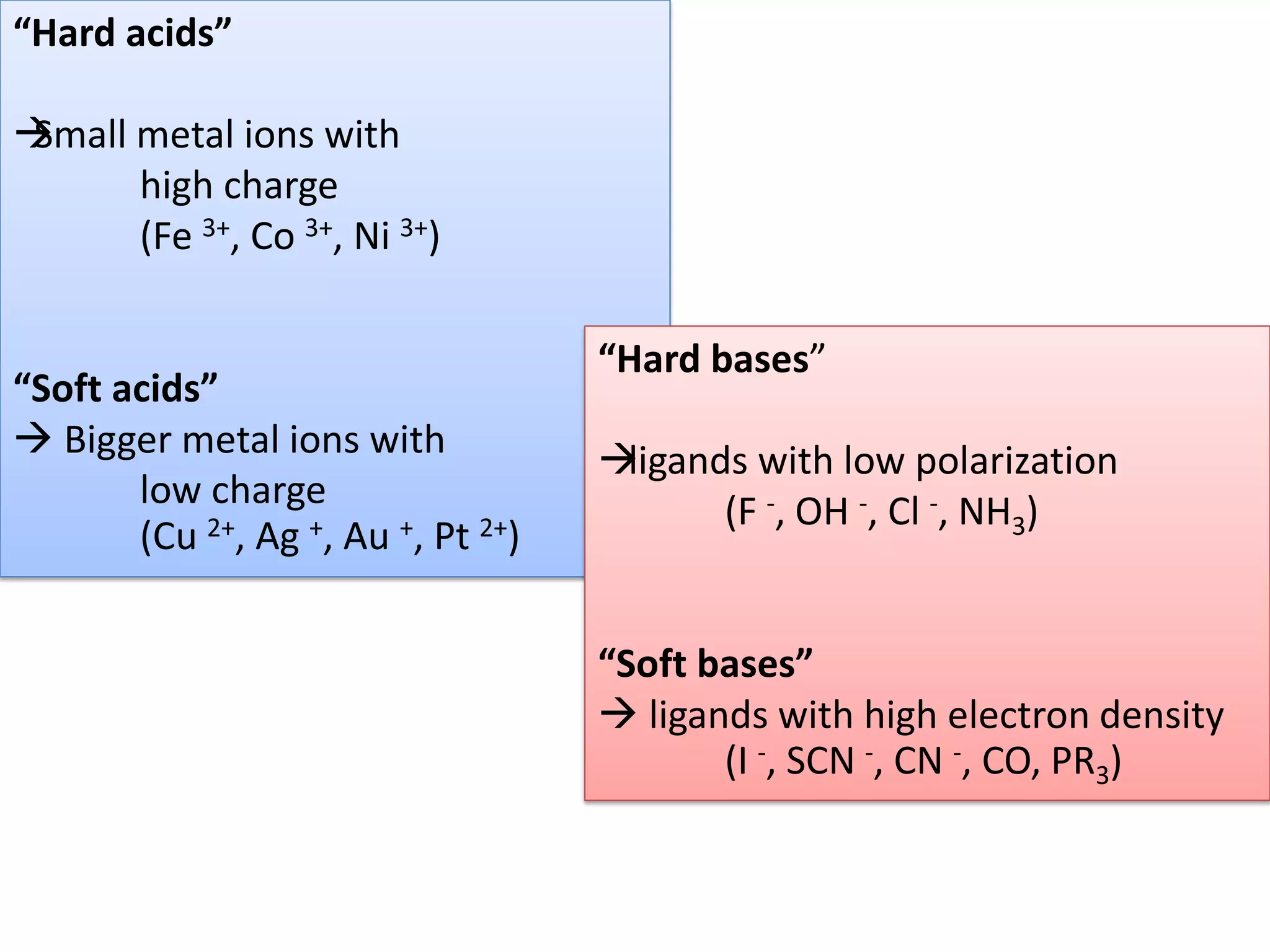
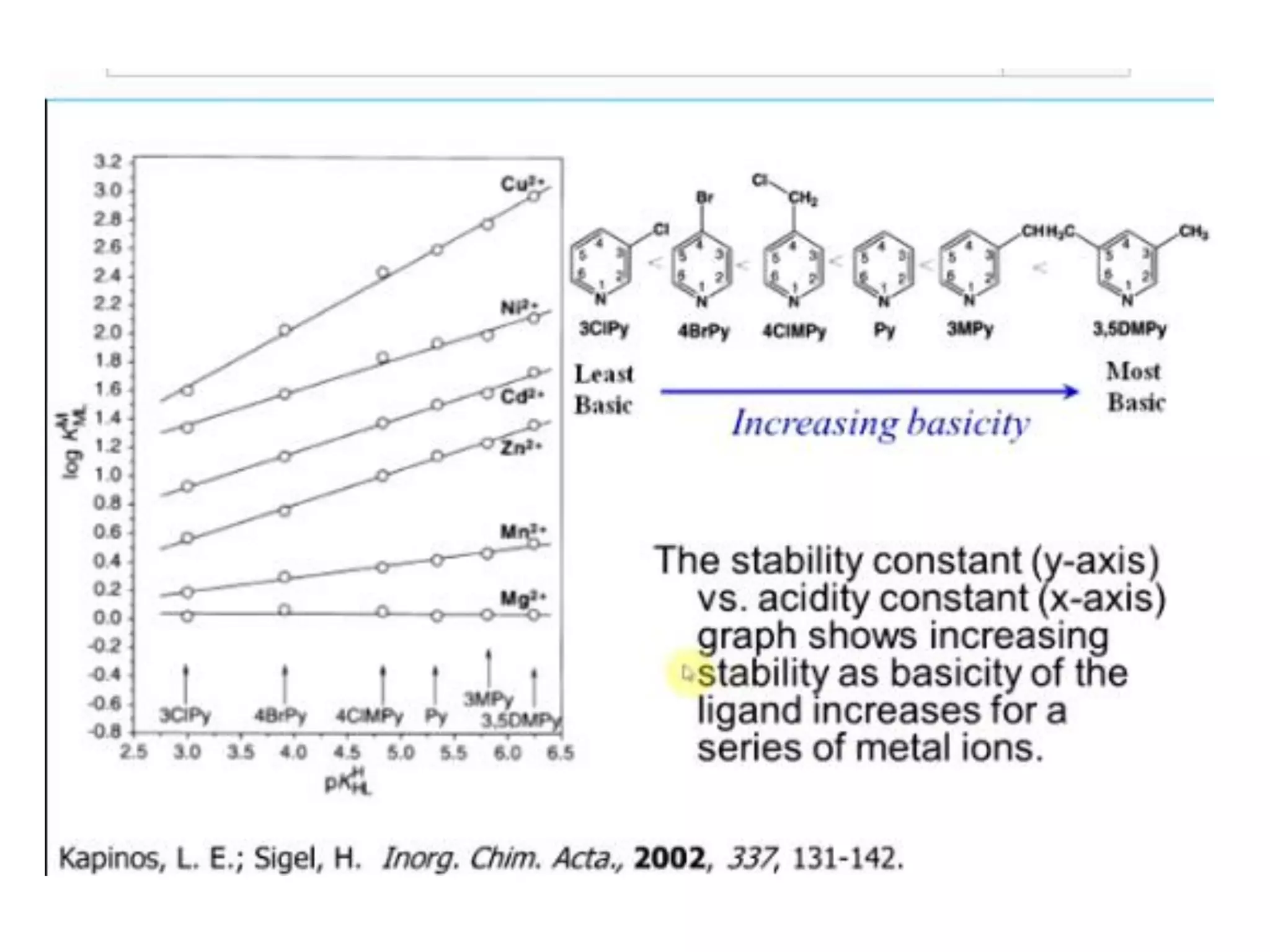
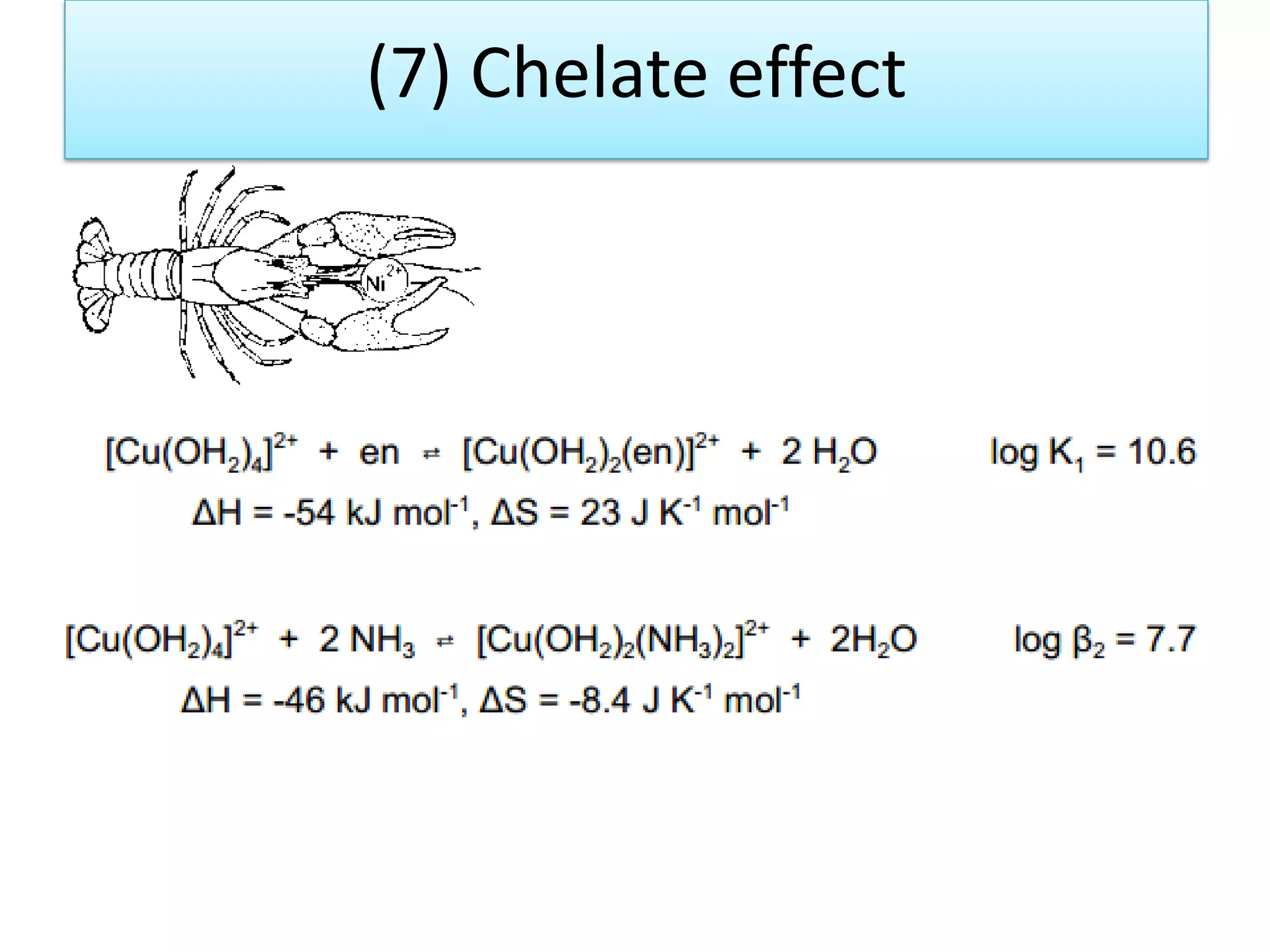
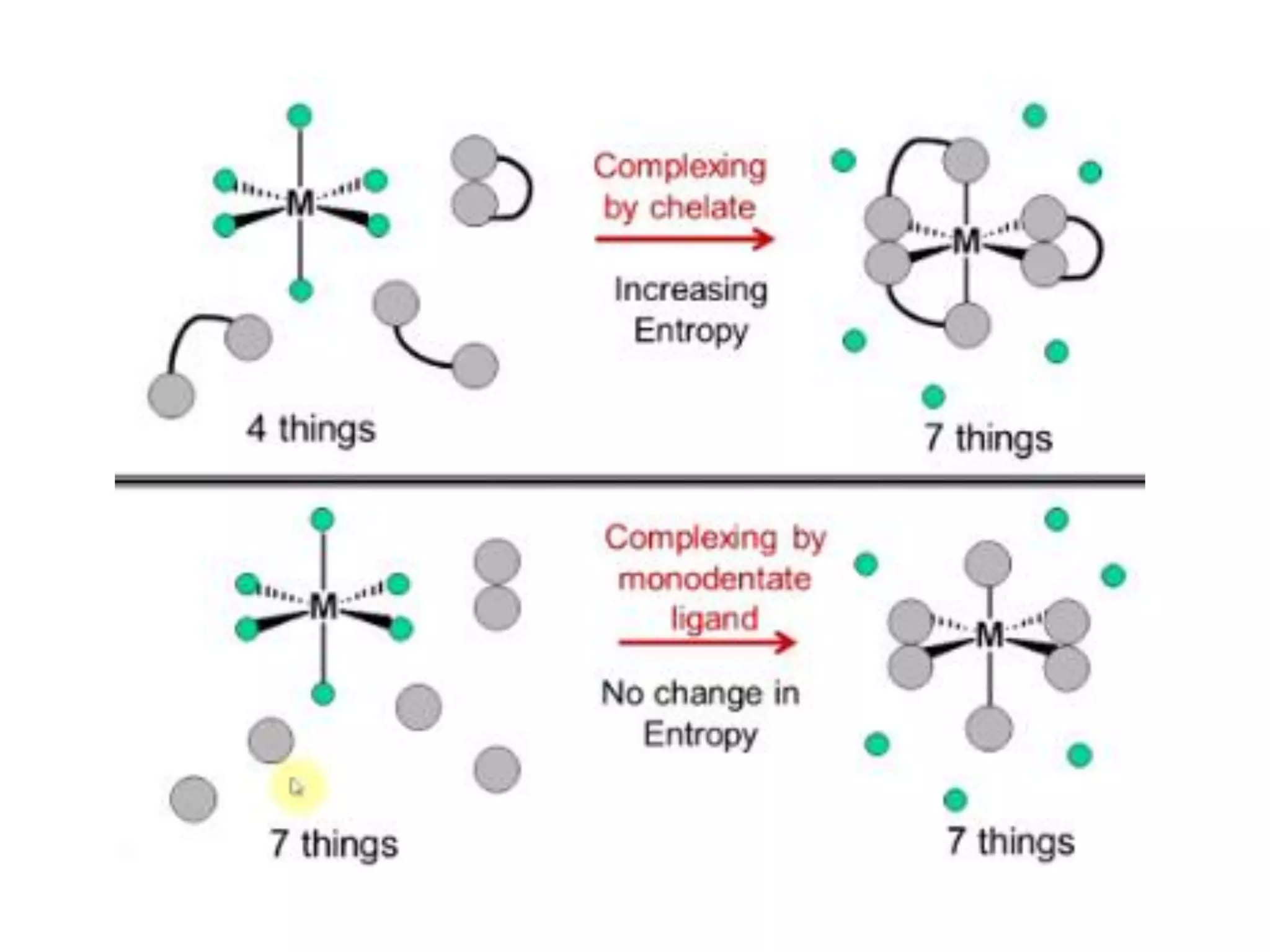
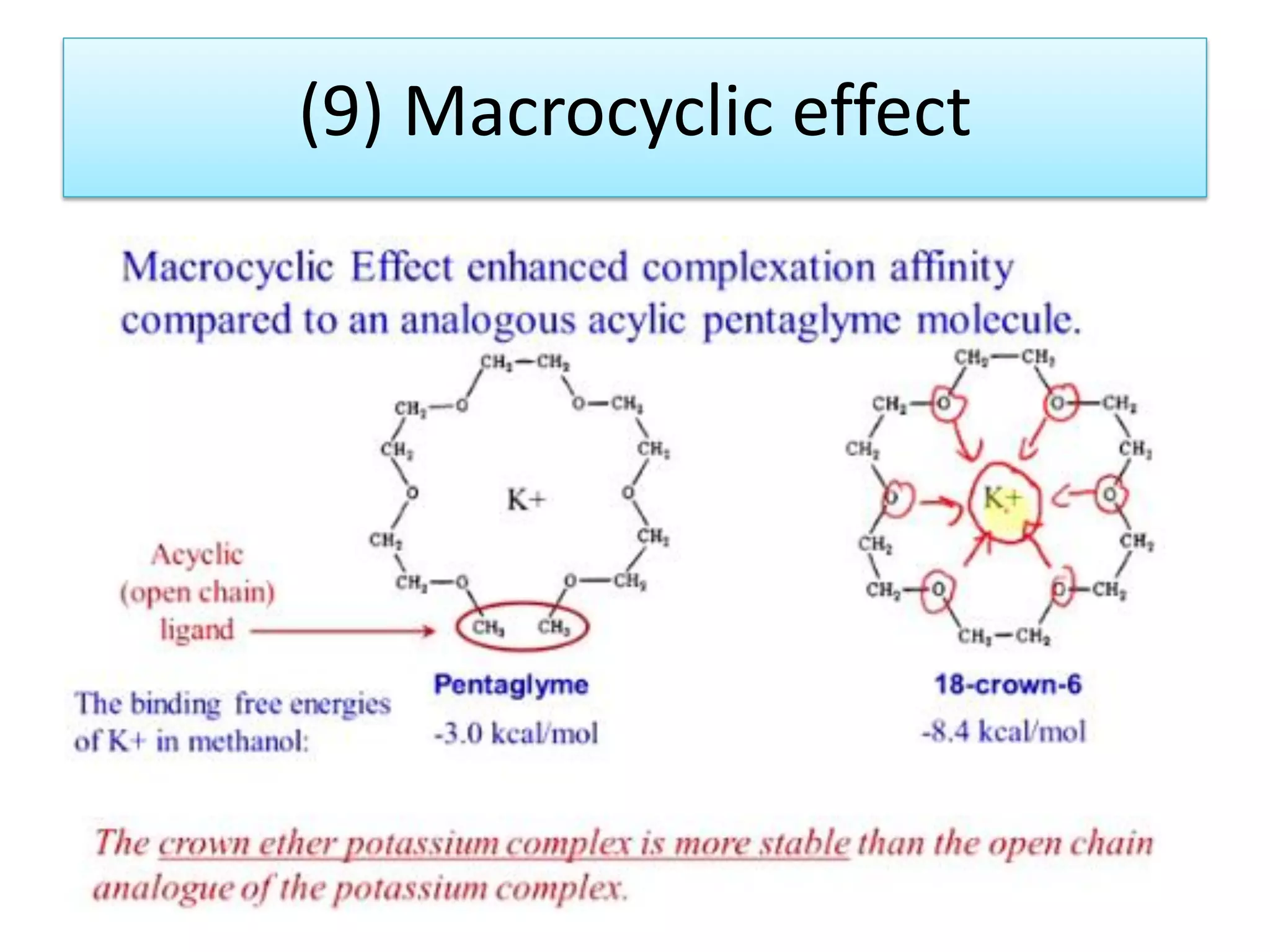
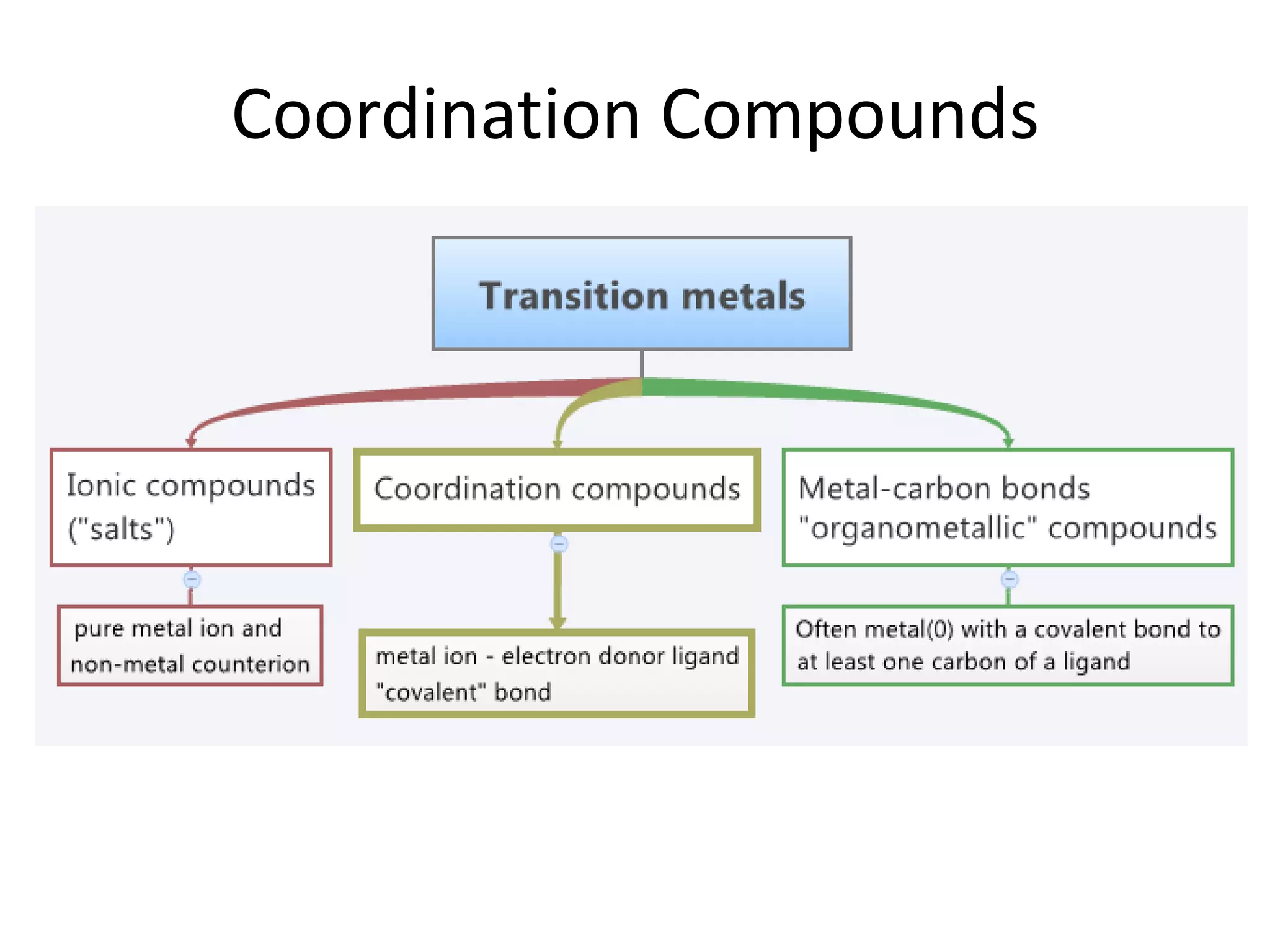
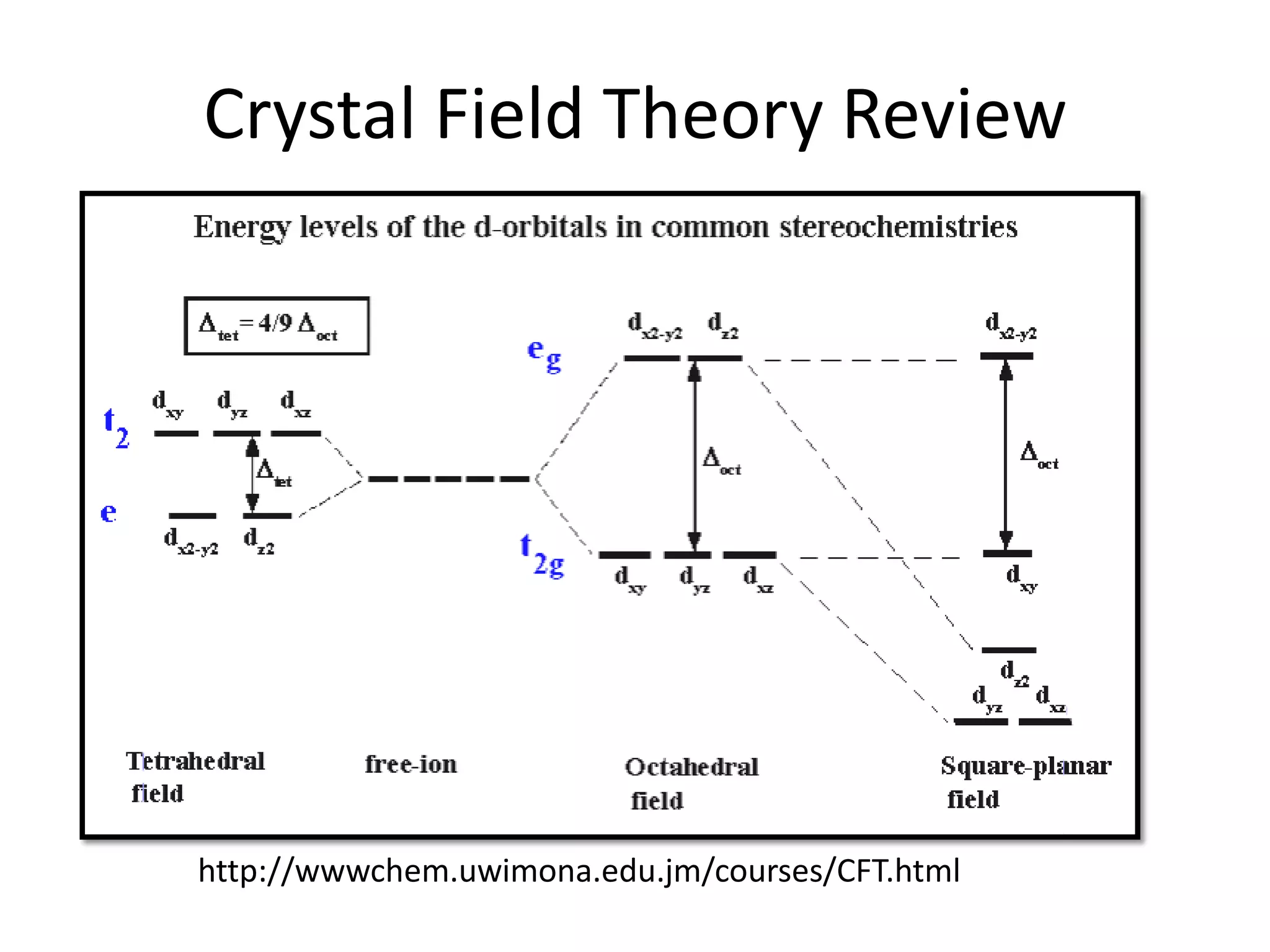
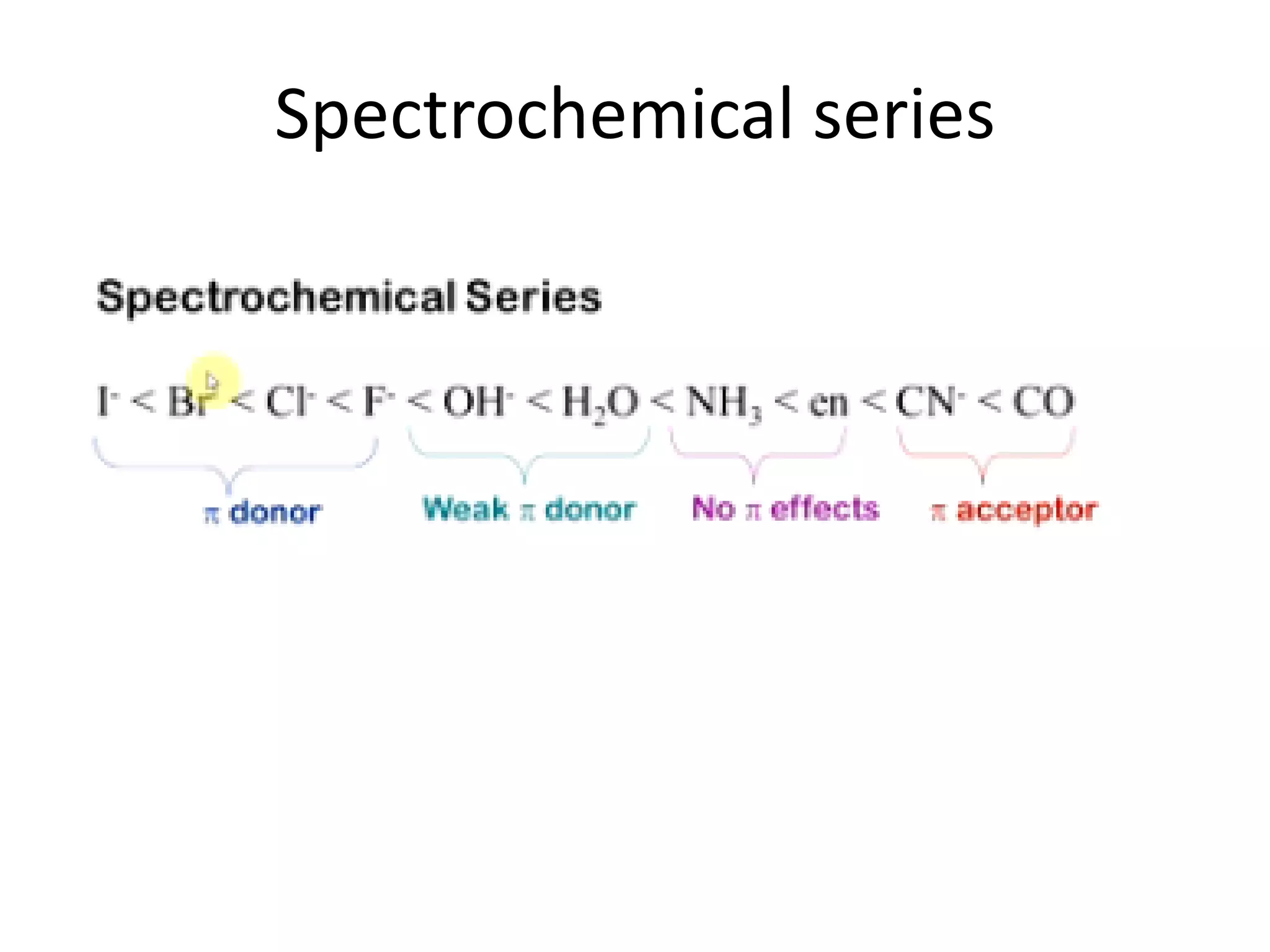
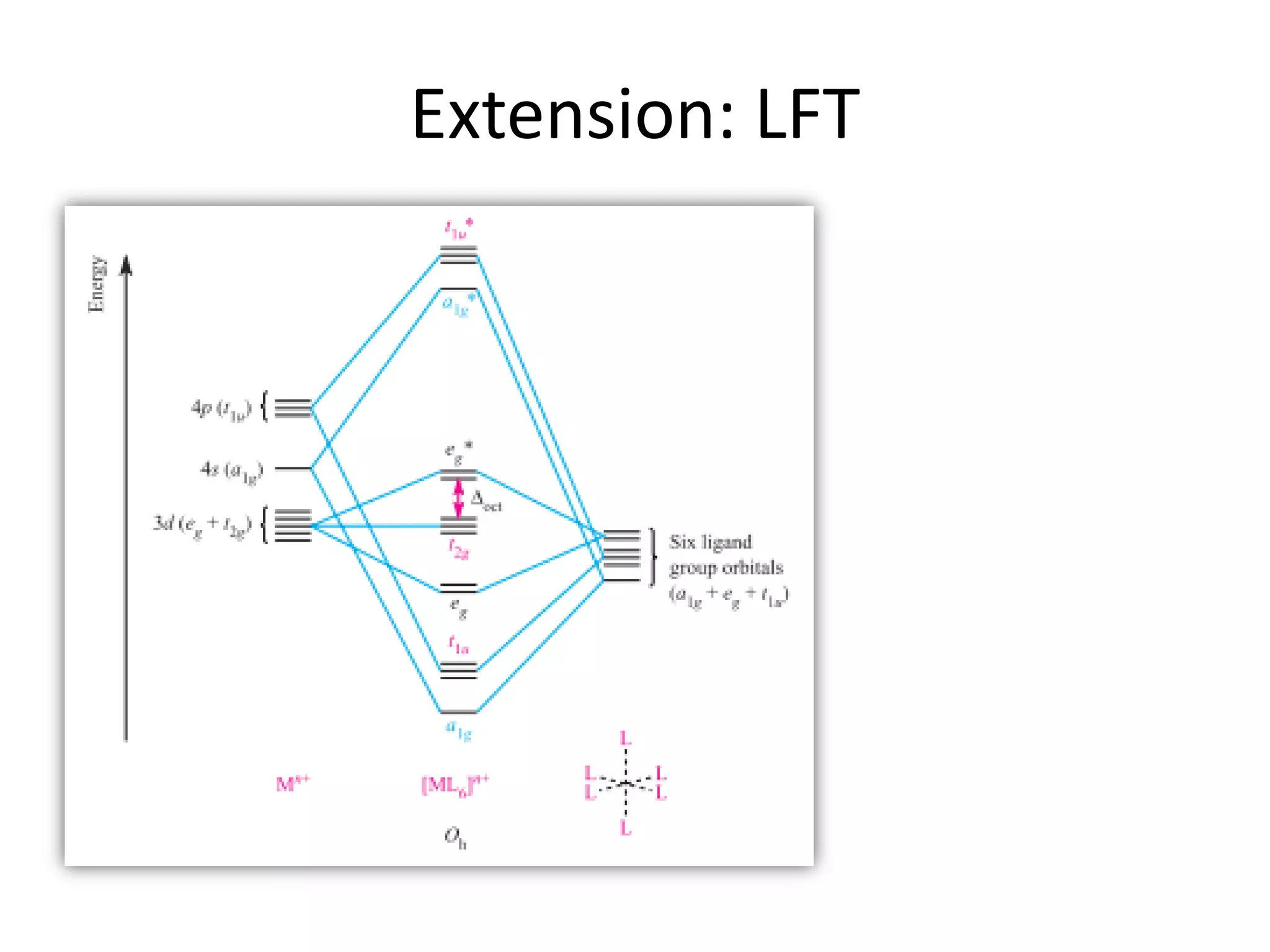
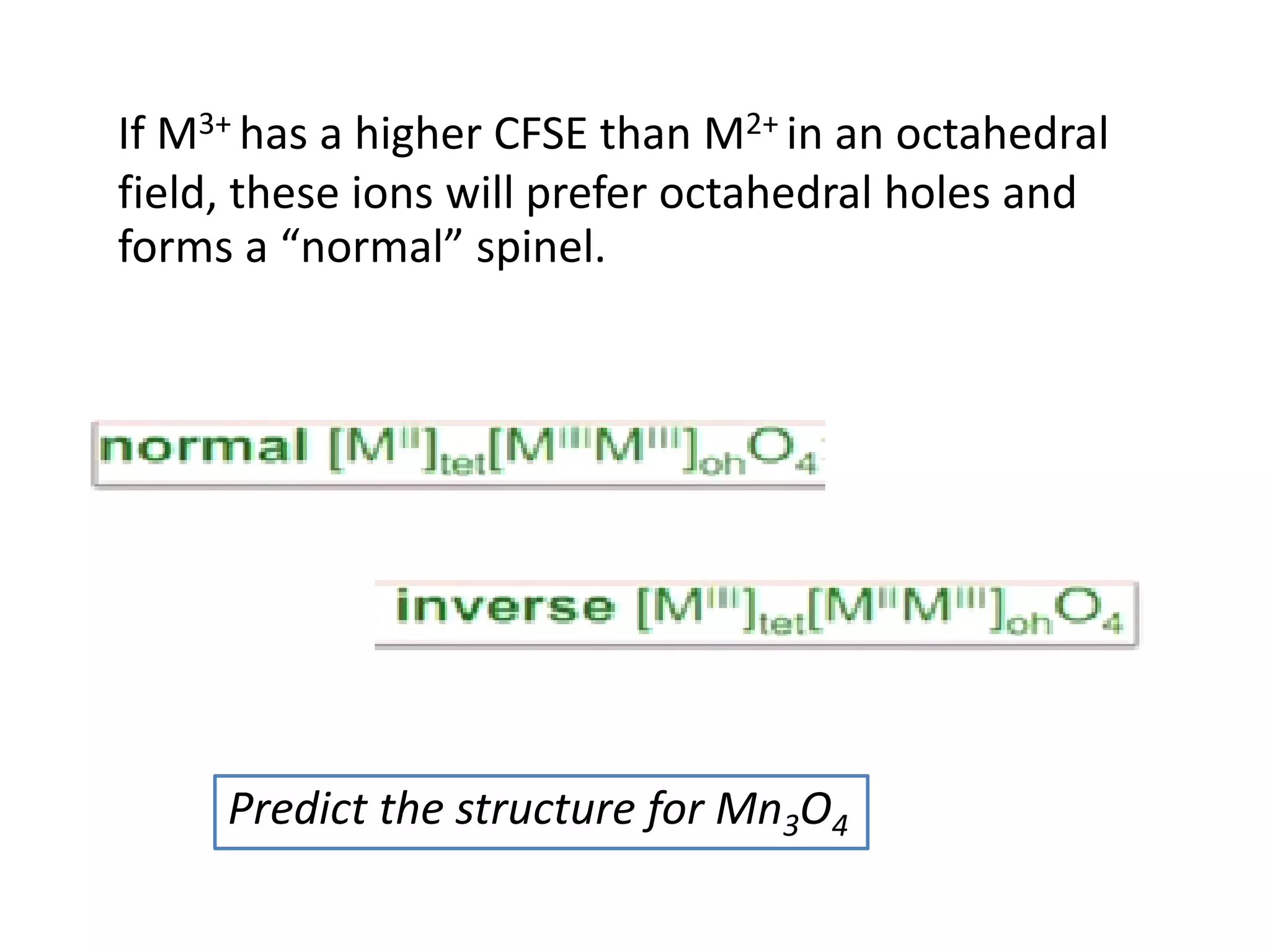
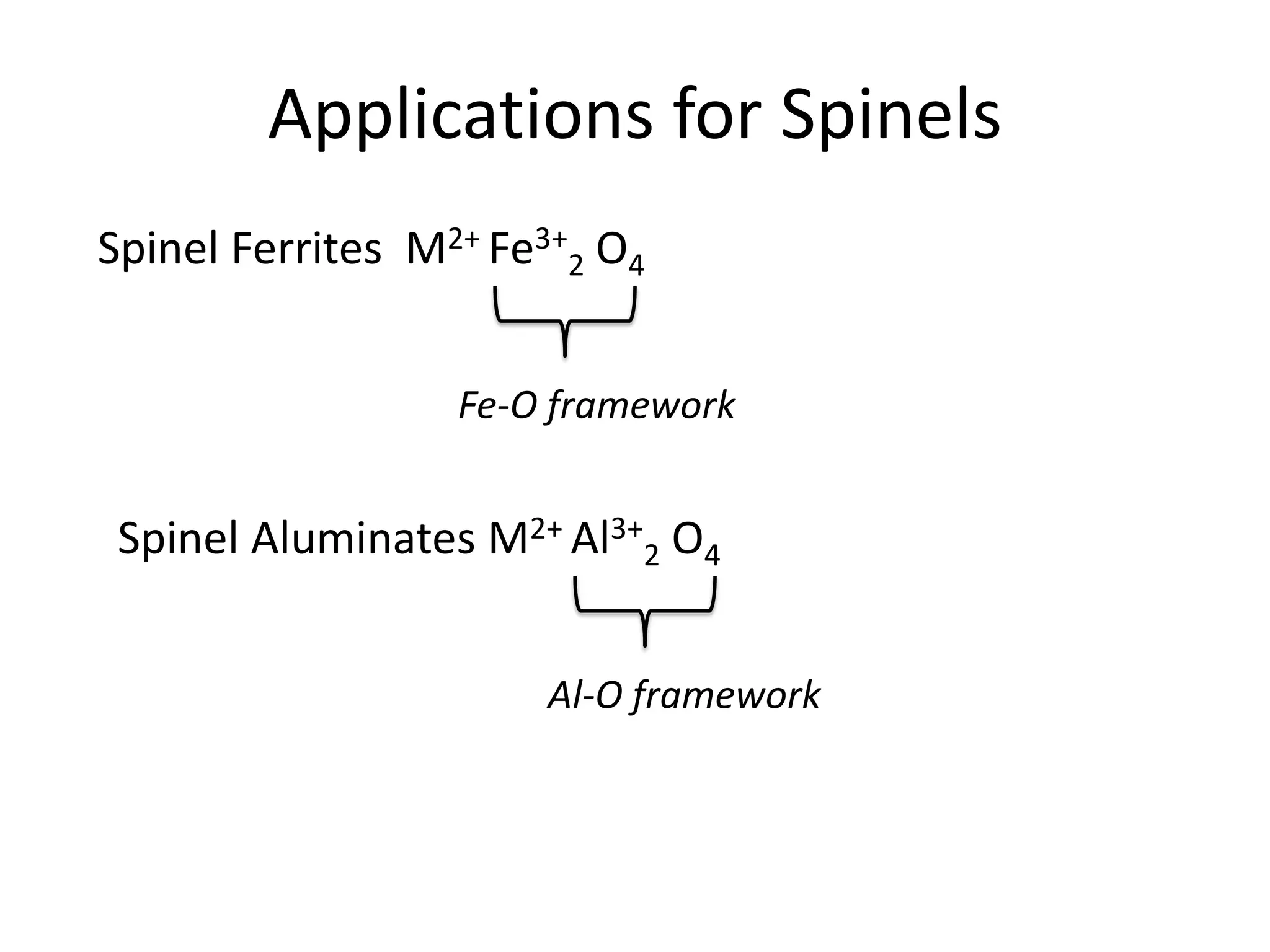
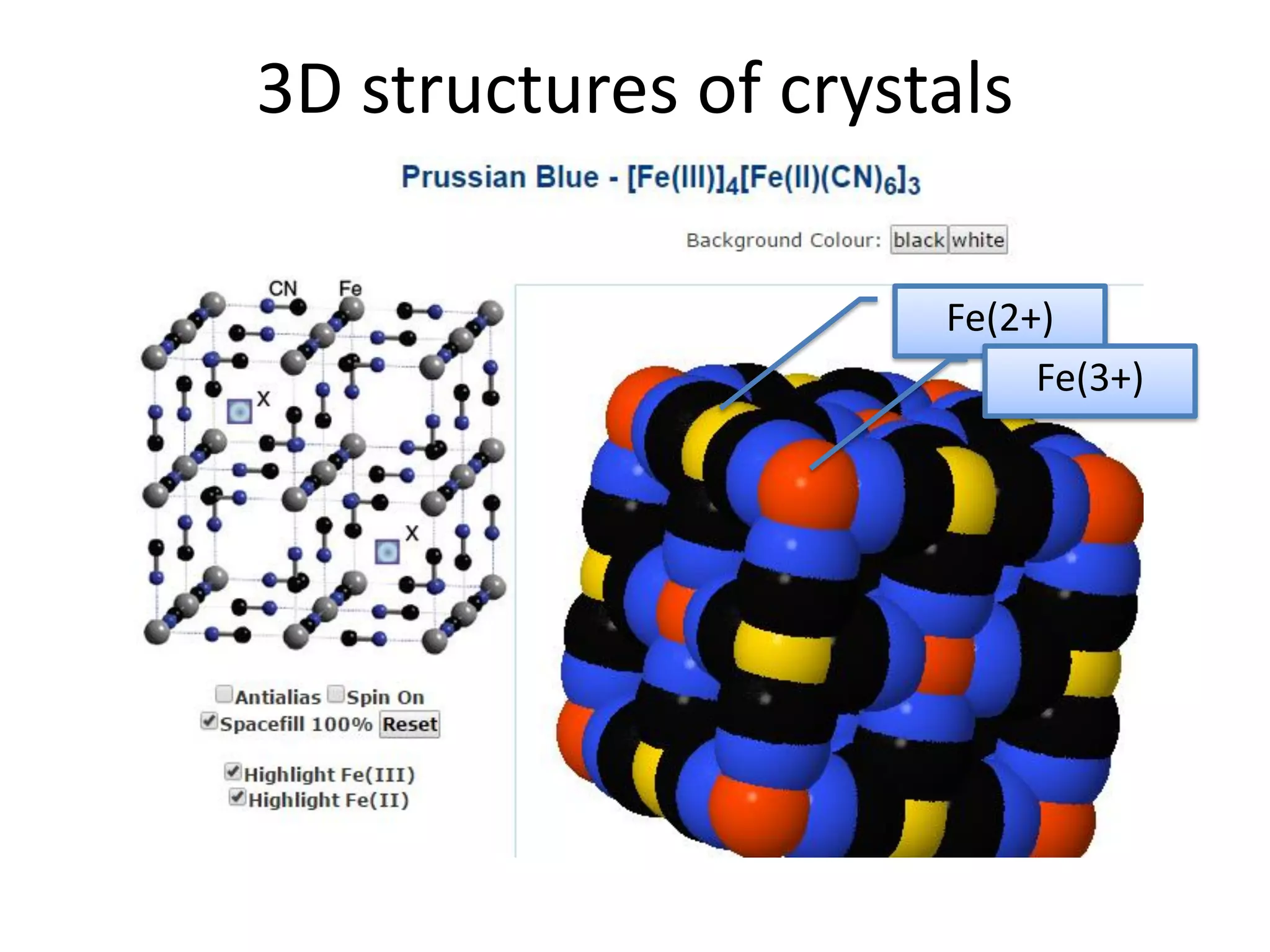
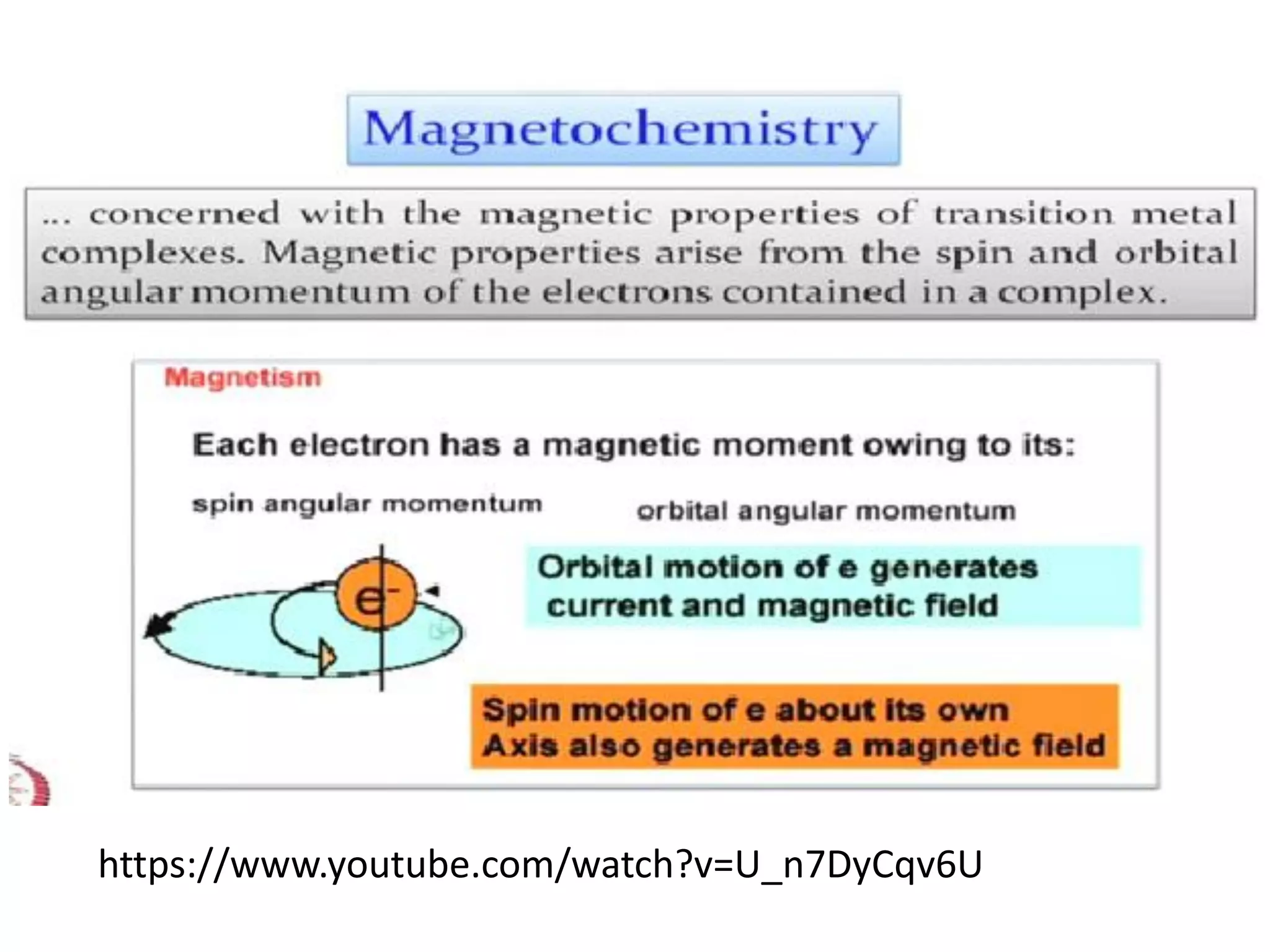
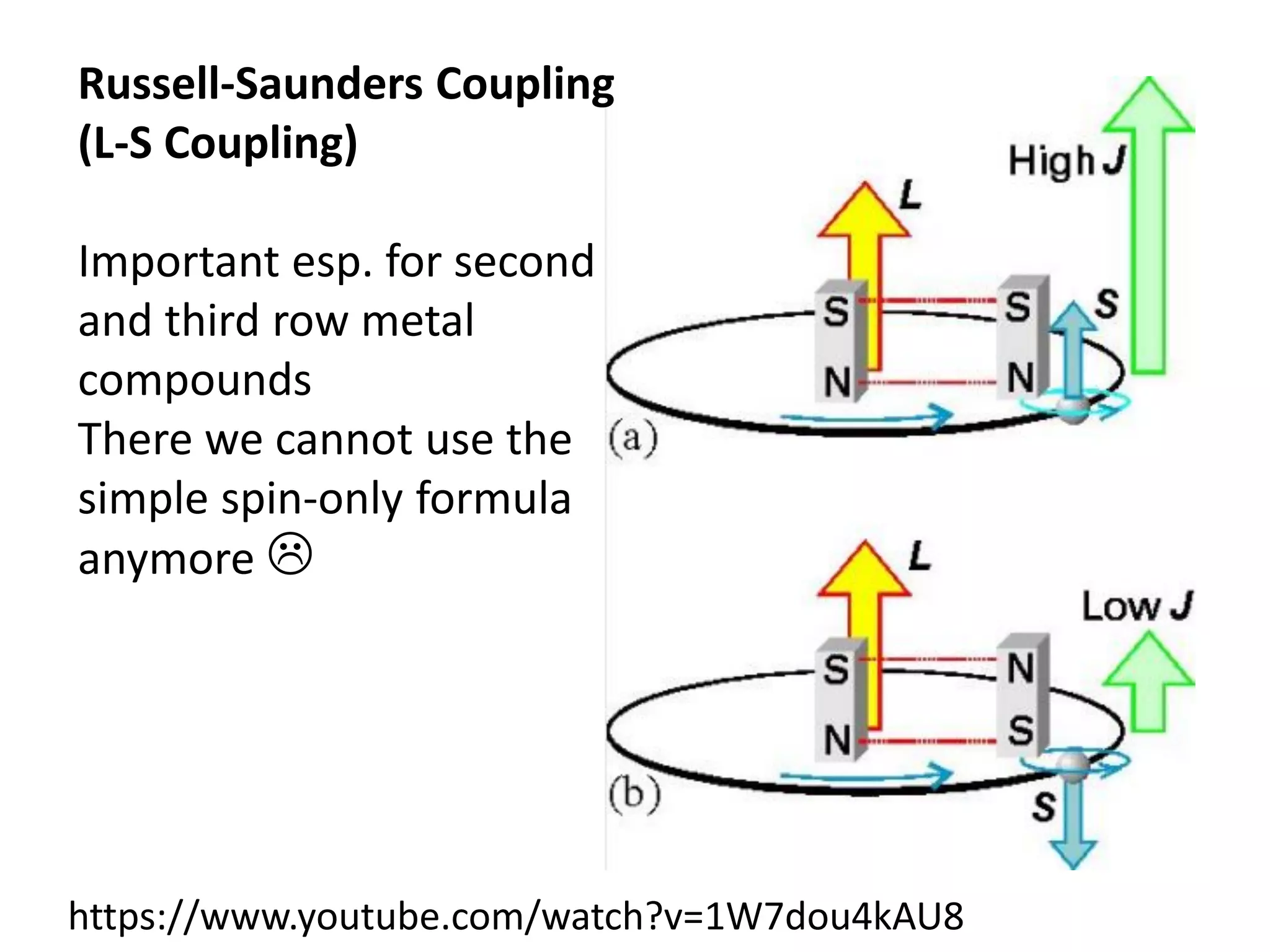
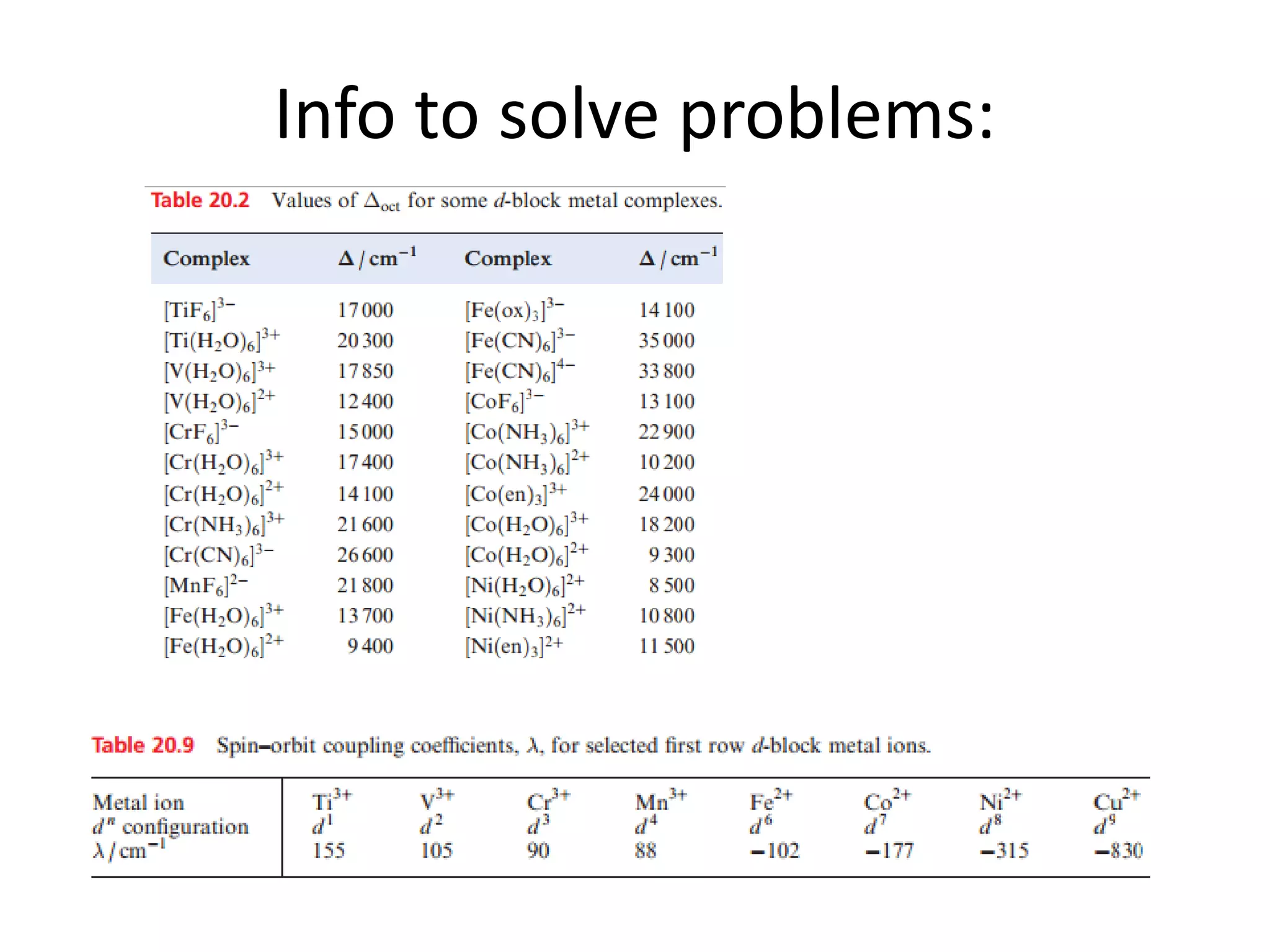
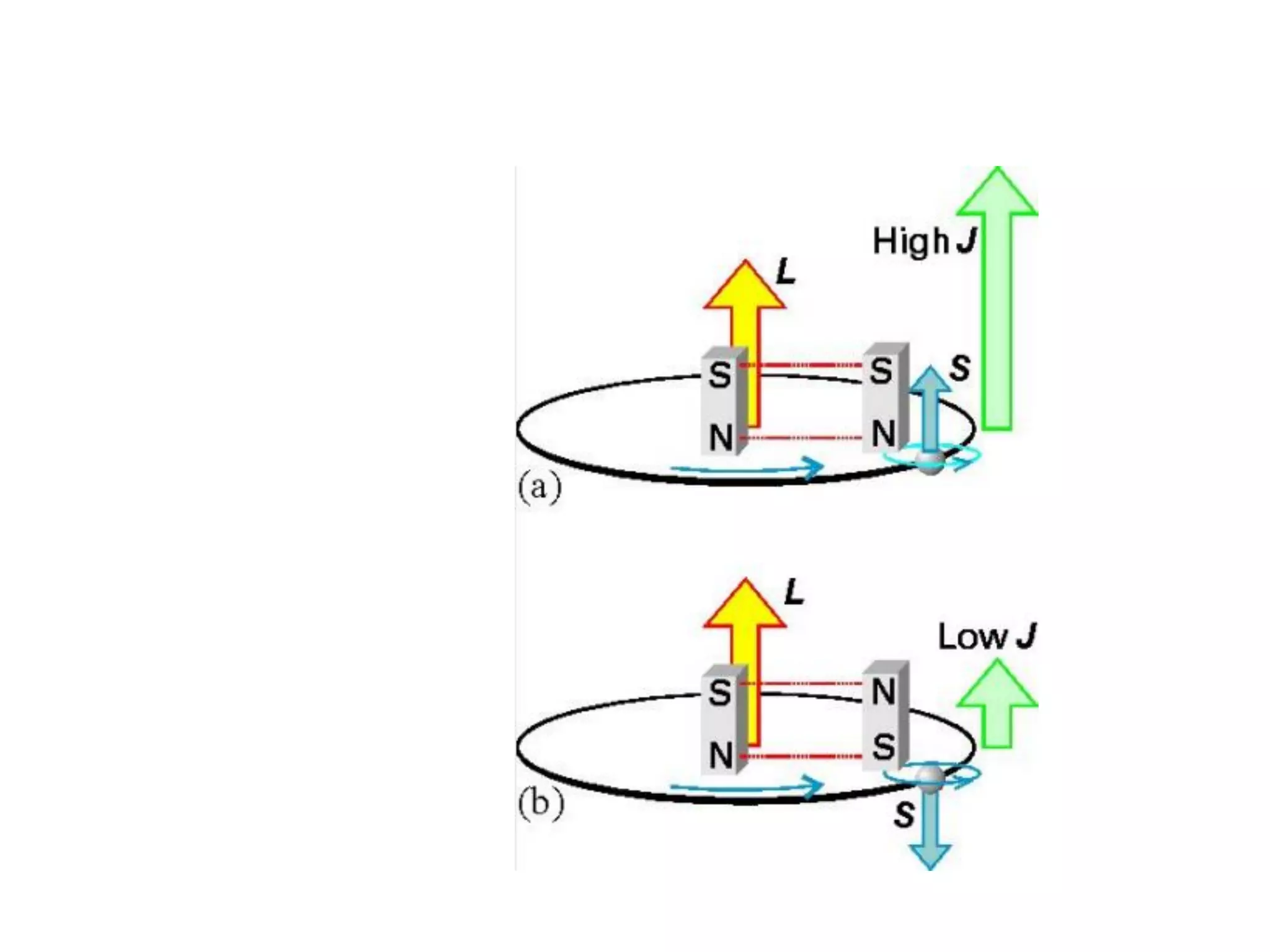
The document discusses the properties of coordination compounds, focusing on various examples and their behavior in precipitation reactions and crystal field theory applications. It covers topics such as electronic spectra, ligand field stabilization energy, and the stability of coordination compounds, including the impact of different ligands on stability and properties. Additionally, it delves into magnetism and the concepts underlying paramagnetism and spin crossover in coordination compounds.

1. Properties of
Coordination Compounds
Dr.Christoph UP 2014

2. Coordination Compounds

3. Example
A) [Cr(NH3)3Cl3]
B) [Cr(NH3)6]Cl3
C) Na3[Cr(CN)6]
D) Na3[CrCl6]
Which of these compounds will form
a precipitation with AgNO3 ?

4. Review: CFT
Applications of Crystal Field Theory

5. Crystal Field Theory Review
http://wwwchem.uwimona.edu.jm/courses/CFT.html

6. http://www.youtube.com/watch?v=LydEaN8-WJ8

7. Spectrochemical series

8. Conclusions from CFT

9. Extension: LFT

10. pi-donor ligands => low splitting

11. pi-acceptor ligands => high splitting

12. Symmetry Symbols
http://www.webqc.org/symmetrypointgroup-td.html

13. Which symmetry do the 5 d-orbitals in a tetrahedron have ?

14. Conclusions from LFT

15. (1) Find the configuration (as tx
2gey
g / ext2
y), the number of
unpaired electrons and the LFSE (in terms of ∆o / ∆t and P)
(2) Which of the following complexes has higher LFSE:
(h) [MnF6]3- i) [NiBr4]2- j) [Fe(CN)6]4-

16. Applications of CFT
(1) Electronic spectra
(2) Hydration energies
(3) Lattice energies
(4) Ionic radii
(5) Spinel types

17. (1) Electronic Spectra (example)
Each peak in the spectrum (λ <-> ν ) corresponds to a change
in the electronic state (Shriver/Atkins p.576)

18. Find ∆o from Tanabe-Sugano diagrams
∆/B
E/B
V(H2O)6
2+ shows 2 peaks at
17200 and 25600 cm-1
(1) Get E-ratio: E2/E1 = 1.49
(2) Find by trial and error this ratio
in the diagram => ∆/B
we find here a value of 40/27 = 29
(3) From this we find B:
E2 = 25600 = 40 *B
E1 = 17200 = 27 *B => B = 640 cm-1
(4) When B is know, then
∆o = 29 * 640 cm-1 = 18600 cm-1

19. http://www.chem.uky.edu/courses/che610/JPS_Spring_2007/
PS2_2007key.pdf
Self-study:

20. Energy ratios:
E2/E1 = 1.8
E3/E1 = 3.05
E3/E1 = 1.68
Now we move on the x-axis until
we find this ratio in the y values
again (approximately !)
=> ∆/B = 10
from that we get B:
E3/B = 29 (graph) => B = 896 cm-1
=> ∆o = 10 * 896 cm-1 = 8960 cm-1
(more exact: take the average for all 3 found B values)

21. (2) Hydration energies
http://www.youtube.com/watch?v=awD1qa7TF4A

23. (3) Lattice energies
Experimental data vs. calculated for MCl2 high-spin
compounds according to the Born-Haber Cycle

24. (4) Ionic Radii M(2+) --- O

25. M2+ ions in water are in a weak field => they are all high-spin
Then we get 2 minima in the radii at V2+ with 3 electrons in the t2g
levels and Ni2+ with 6 electrons in t2g
For low-spin there is only one minima at Fe2+ with 6 electrons in t2g

26. (5) Spinels (gemstones)
Spinels = crystals formed by mixed oxides,
originally used for MgAl2O4
In a closed packed solid, there are tetrahedral and
octahedral “holes” filled with a metal ion.
“ cubic closed packing”
(https://www.youtube.com/watch?v=U_n7DyCqv6U)

27. Example
What is the oxidation number of Fe in Fe3O4 ?

28. “normal”: A in Td , B in Oh holes
Fe3O4 is a spinel type : Fe2+ (Fe3+ )2 O4
“inverse”: A in Oh,
1/2B in Td and 1/2B in Oh
(neglectpairingenergyP)
http://www.everyscience.com/Chemistry/Inorganic/
Crystal_and_Ligand_Field_Theories/e.1016.php
“Magnetite”

29. If M3+ has a higher CFSE than M2+ in an octahedral
field, these ions will prefer octahedral holes and
forms a “normal” spinel.
Predict the structure for Mn3O4

30. Applications for Spinels
Spinel Ferrites M2+ Fe3+
2 O4
Fe-O framework
Spinel Aluminates M2+ Al3+
2 O4
Al-O framework

31. https://www.youtube.com/watch?v=U_n7DyCqv6U

34. Visualization of molecules and orbitals
www.chemtube3d.com

35. 3D structures of crystals
Fe(2+)
Fe(3+)

37. Magnetism
(extensive explanations:
https://www.youtube.com/watch?v=U_n7DyCqv6U)

38. https://www.youtube.com/watch?v=U_n7DyCqv6U

39. Ferro-, Ferri-, Antiferro-, Para-
Magnetism
http://en.wikipedia.org/wiki/Curie_temperature

40. Para-magnetism
Atoms that have unpaired electrons (also metals) and
therefore a total electron-spin S.
These individual magnetic moments can be oriented by
an outer magnetic field to line up.
Paramagnetic substances are not magnetic by
themselves but can become magnetic when an outer
field is applied.
Every ferromagnetic material has a Curie-Temperature
Tc where it loses its permanent magnets and becomes
para-magnetic.

41. Curies Law
Describes the “magnetic susceptibility” of a
material dependent on the outer field B and
Temperature T
=> High magnetization M:
(a) High external field B
(b) Low temperature
Or: ‘chi”
= magn.
susceptibility

42. Curies Temperature Tc
Heating up a permanent magnet brings the spins to
become randomly oriented (at temperature Tc)
-> the material loses its magnetism but can still
become magnetic again in an external field

43. https://www.youtube.com/watch?v=1W7dou4kAU8

44. http://www.youtube.com/watch?v=u36QpPvEh2c
Dia- and Para-Magnetism

45. Magnetic Properties
Paramagnetism arises from unpaired electrons.
Each electron has a magnetic moment with
one component associated with the spin
angular momentum of the electron and
(except when the quantum number l ¼0) a
second component associated with the orbital
angular momentum.
(p.579)

46. Where does magnetism come from ?

47. Effect of unpaired electrons
http://www.youtube.com/watch?v=qfooM_Gl69k

48. Gouy Balance

49. http://wwwchem.uwimona.edu.jm/utils/gouy.html

50. Spin-only formula

51. Examples

52. Conclusions from magn. susceptibility

54. Spin Cross Over SCO
Some complexes can change from low-spin to high-
spin at higher temperatures:
=> low magnetic moment -> high m.m.
=> M-L bonds short -> longer
(why ?)
This can happen quickly in a small T-range
http://www.youtube.com/watch?v=e9SMMA9Xe9c

55. SCO applications

56. Spin and orbital contributions to the
magnetic moment
If S-L coupling is weak

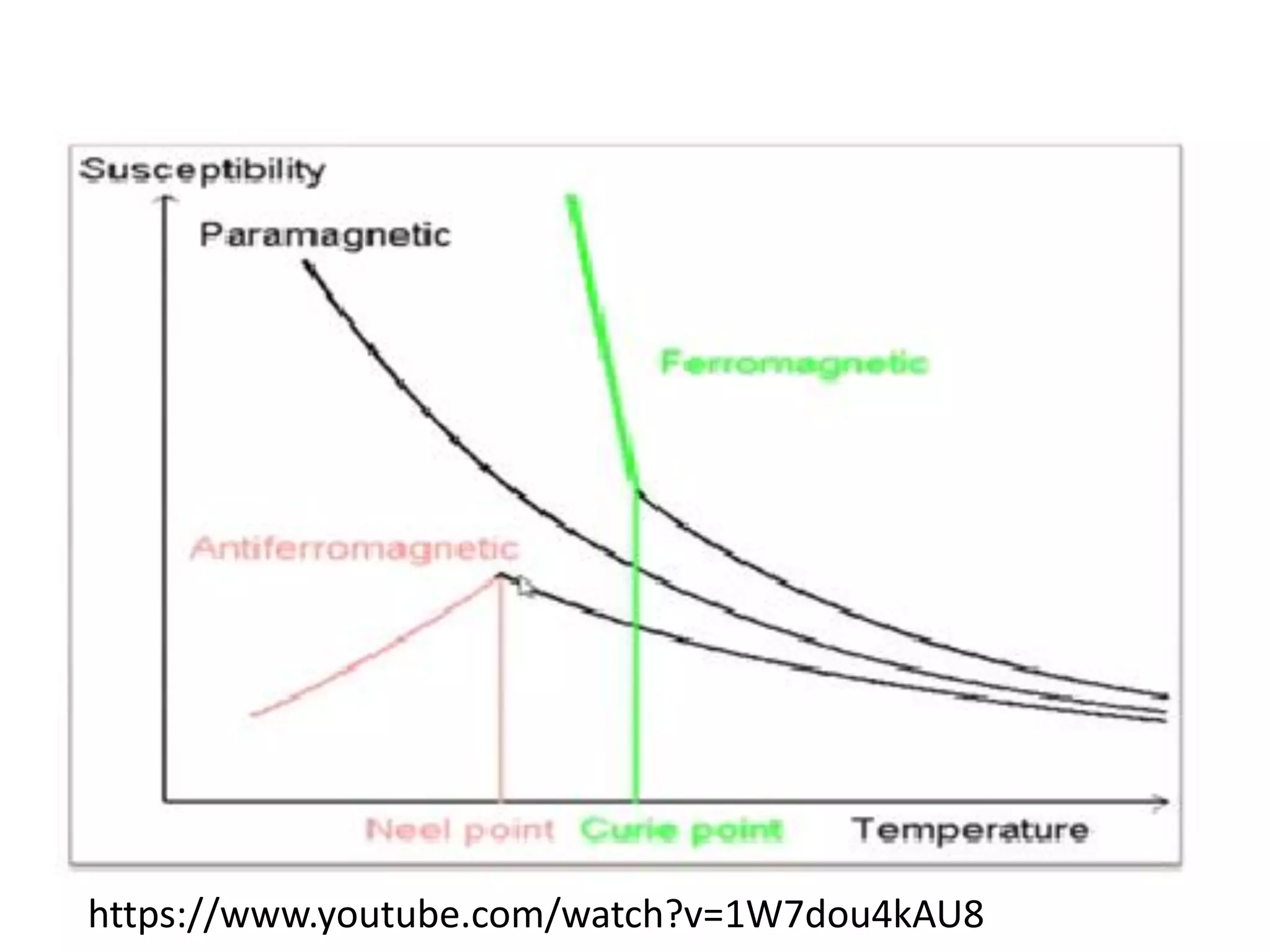
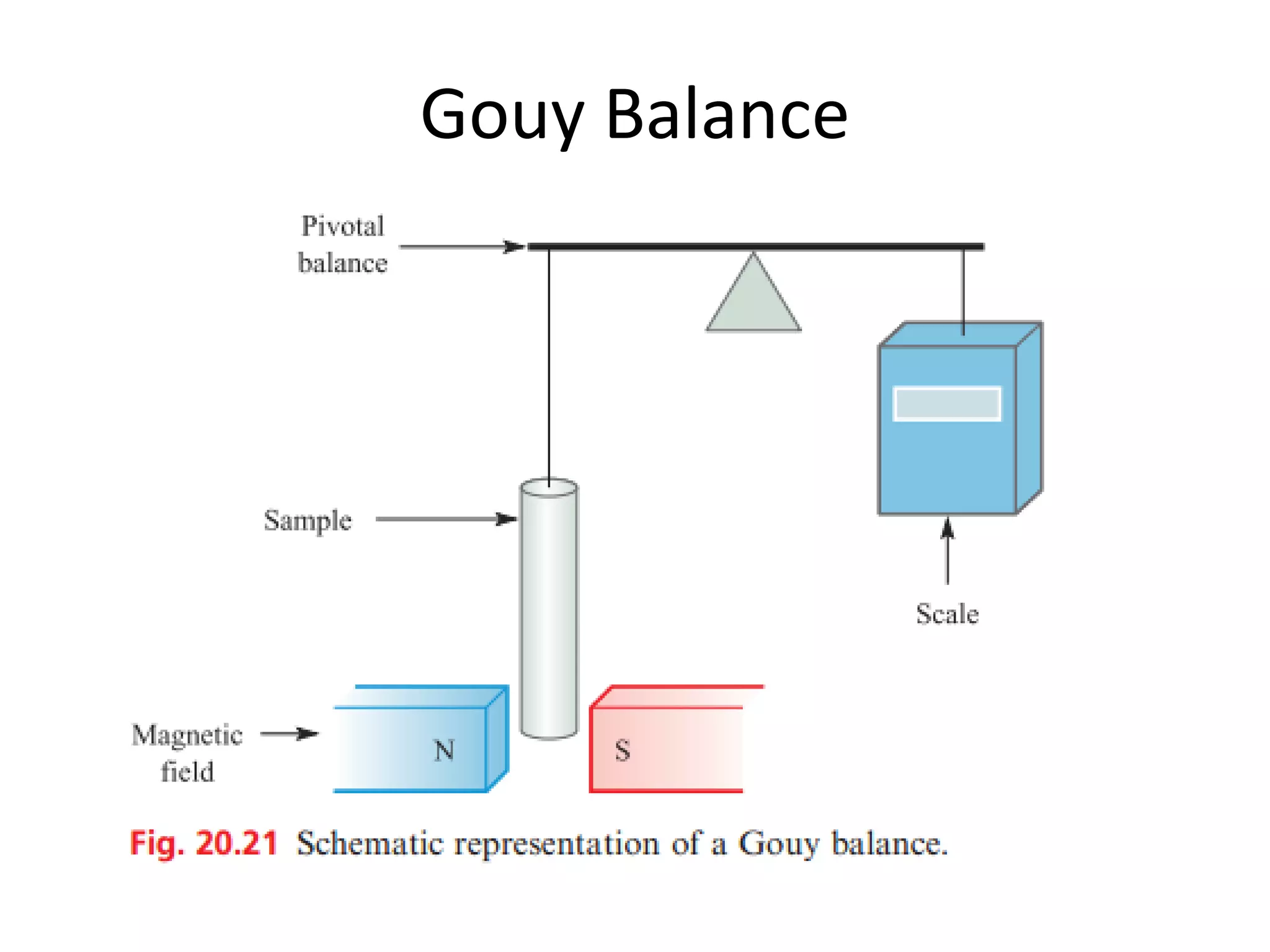
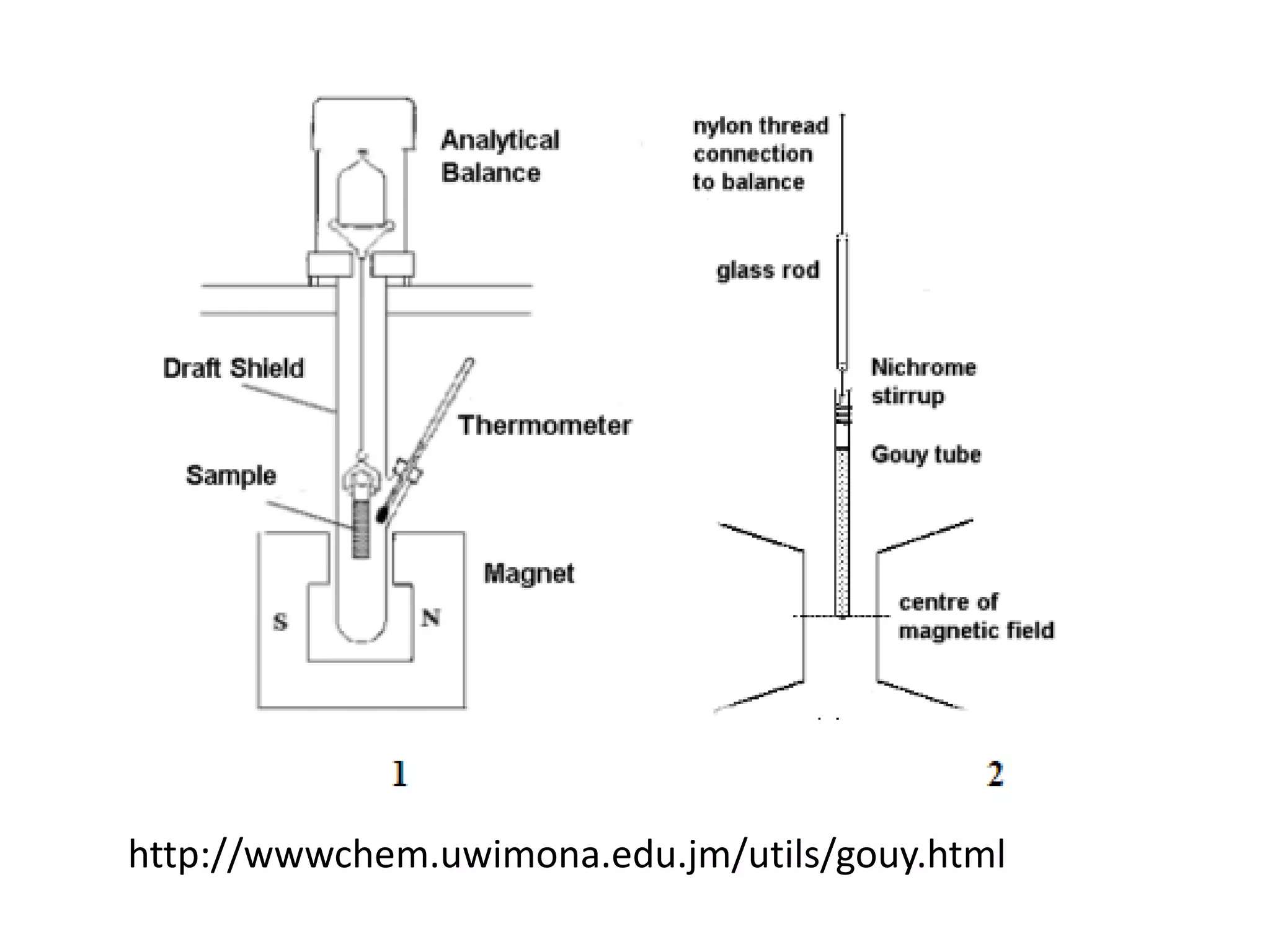
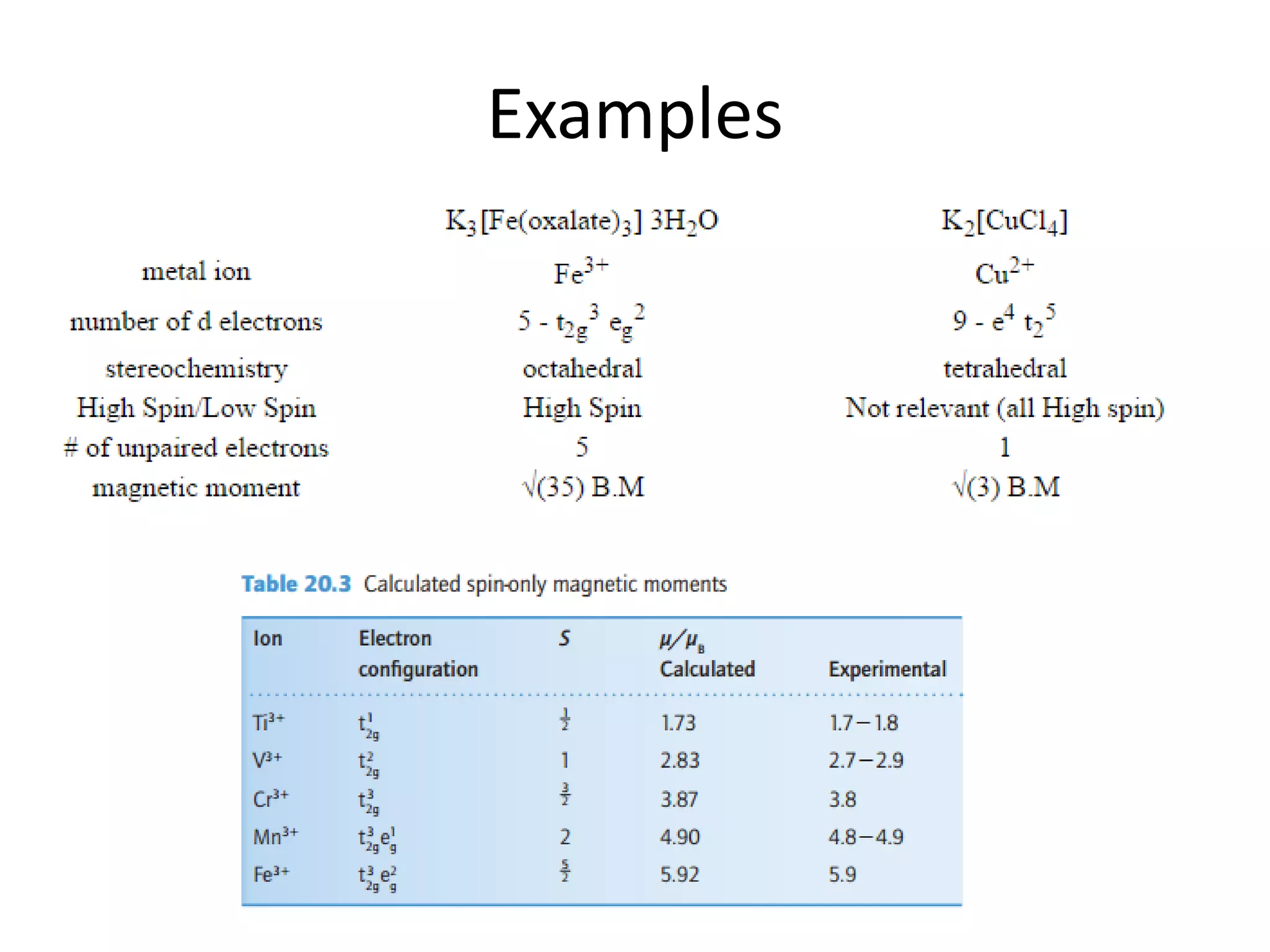
57. Deviations from spin-only formula
Example:
[Fe(CN)6]3- has μ = 2.3μB
which is between low- and high-spin calculated
(check this out)

58. Russell-Saunders Coupling
(L-S Coupling)
Important esp. for second
and third row metal
compounds
There we cannot use the
simple spin-only formula
anymore 
https://www.youtube.com/watch?v=1W7dou4kAU8

59. Spin-orbitcoupling
Is higher than spin-only – typical for d-complexes
with more than half-filled d-shell

60. Info to solve problems:

61. Spin-Orbit coupling
Russell-Saunders Coupling

63. Electronic states review
Alternative to state the electron configuration of
an ion as 4s2 3d6, we can express this
configuration as “microstates”:
Ti(3+):
4s0 3d1
Microstates:
S = ½
L = 2 (“d”)
=> J = 5/2, 3/2 ( L+S),(L+S-1),…(L-S)
Ground State with lowest J: 2D3/2

66. Examples

68. Attkins p.505

69. Stability of coordination
compounds

70. http://wwwchem.uwimona.edu.jm/courses/IC10Kstability.html

71. Thermodynamic stability
(equilibrium constant)
http://chimge.unil.ch/En/complexes/ressources/cpxenc.pdf

72. Equilibrium constant K and β
http://www.youtube.com/watch?v=LydEaN8-WJ8

73. Entropy effect

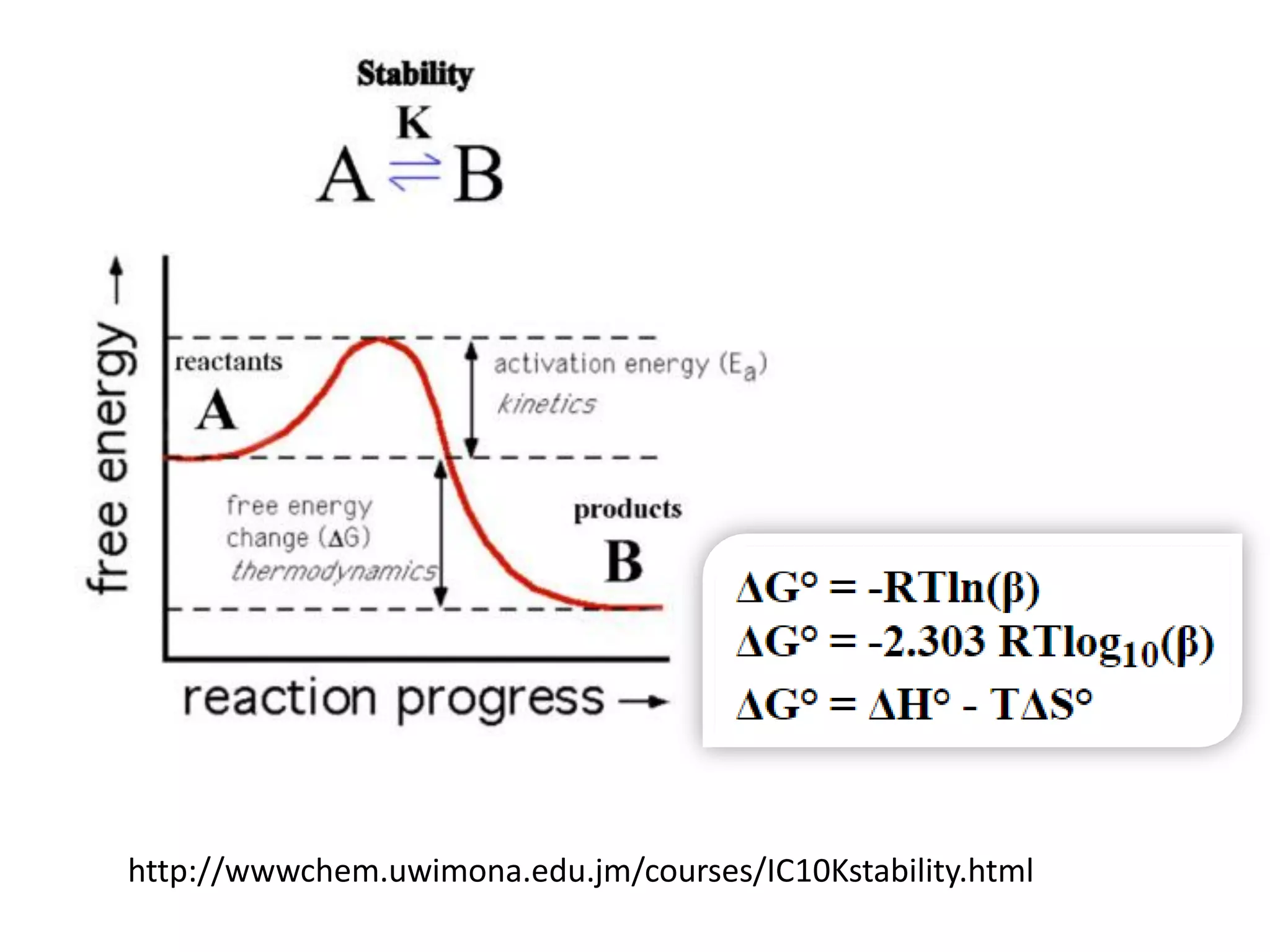
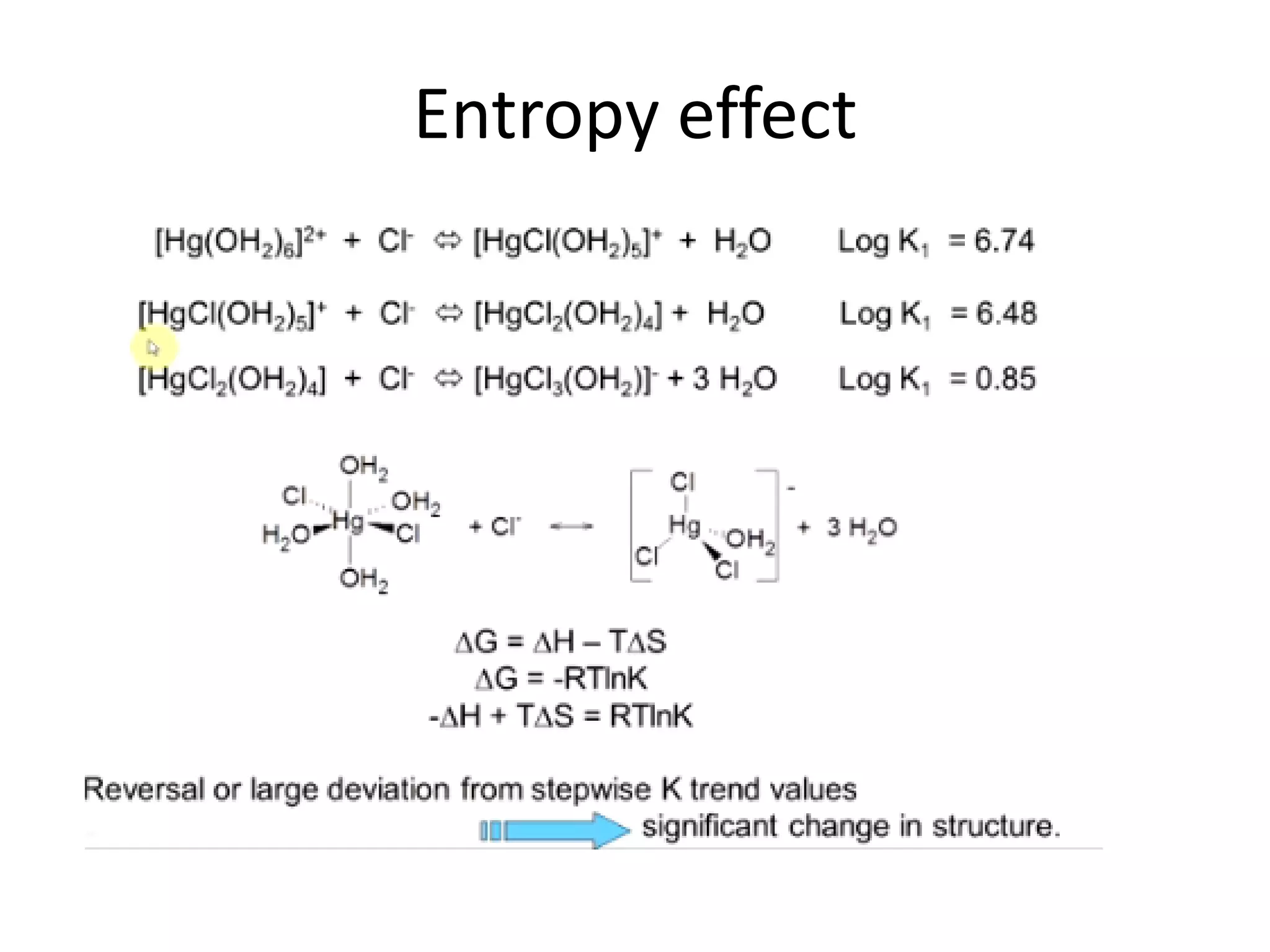
75. Example 1
Assume that in the reaction of Cu2+ with ammonia,
the only complex ion to form is the tetra-ammine
species, [Cu(NH3)4]2+.
Given a solution where the initial [Cu2+] is 0.10M,
and the initial [NH3] is 1.0M and that β4 = 2.1 x 1013,
calculate the equilibrium concentration of the
Cu2+ ion.
http://wwwchem.uwimona.edu.jm/courses/IC10K1.html

78. Examples
Calculate the equilibrium concentration of the Fe3+ ion in a
solution that is initially 0.10 M Fe3+ and 1.0 M SCN-, given that
β2 for Fe(SCN)2
+ = 2.3 x 103

79. (1) Irving-Williams series
M-L bonds become more
covalent

80. Hydration energy
gets higher if LFSE is
more negative !
(2) Ligand Field Stabilization Energy

81. (3) Jahn-Teller Effect
Estimate which d-orbital occupation(s) can cause a JT
effect ….. (distinguish between high- and low-spin)

83. Example Cr(II)(H2O)6
Why is a
distortion to D4h
preferred over
regular Oh ?

84. Solution:
estimate the LFSE for both symmetries
For both symmetries, the 3 electrons in the lower
levels have LFSE = 3 (-3/5 ∆o)
But the one electron in the upper level is lower in
energy for D4h
therefore the total LFSE is more negative (more stable)

85. (4) HSAB principle

86. “Hard acids”
Small metal ions with
high charge
(Fe 3+, Co 3+, Ni 3+)
“Soft acids”
 Bigger metal ions with
low charge
(Cu 2+, Ag +, Au +, Pt 2+)
“Hard bases”
ligands with low polarization
(F -, OH -, Cl -, NH3)
“Soft bases”
 ligands with high electron density
(I -, SCN -, CN -, CO, PR3)

89. “basicity”  high electron density

91. Estimate basicity of molecules
Order these ligands from lowest to highest basicity
NH3 PH3 P(CH3)3 SR2
F- Br- OH- CN-
Main effect is the electron density !
Determined by:
electronegativity of atom with lone pair
and/or electron-pull or donate effect of neighbor atoms

92. (7) Chelate effect

94. Example
the driving force is the increase in entropy

96. Conclusion
Complexes formed by multidentate ligands are much
more stable than those formed by “normal” ligands !

97. (8) Bulk and Size of Ligands

98. (9) Macrocyclic effect