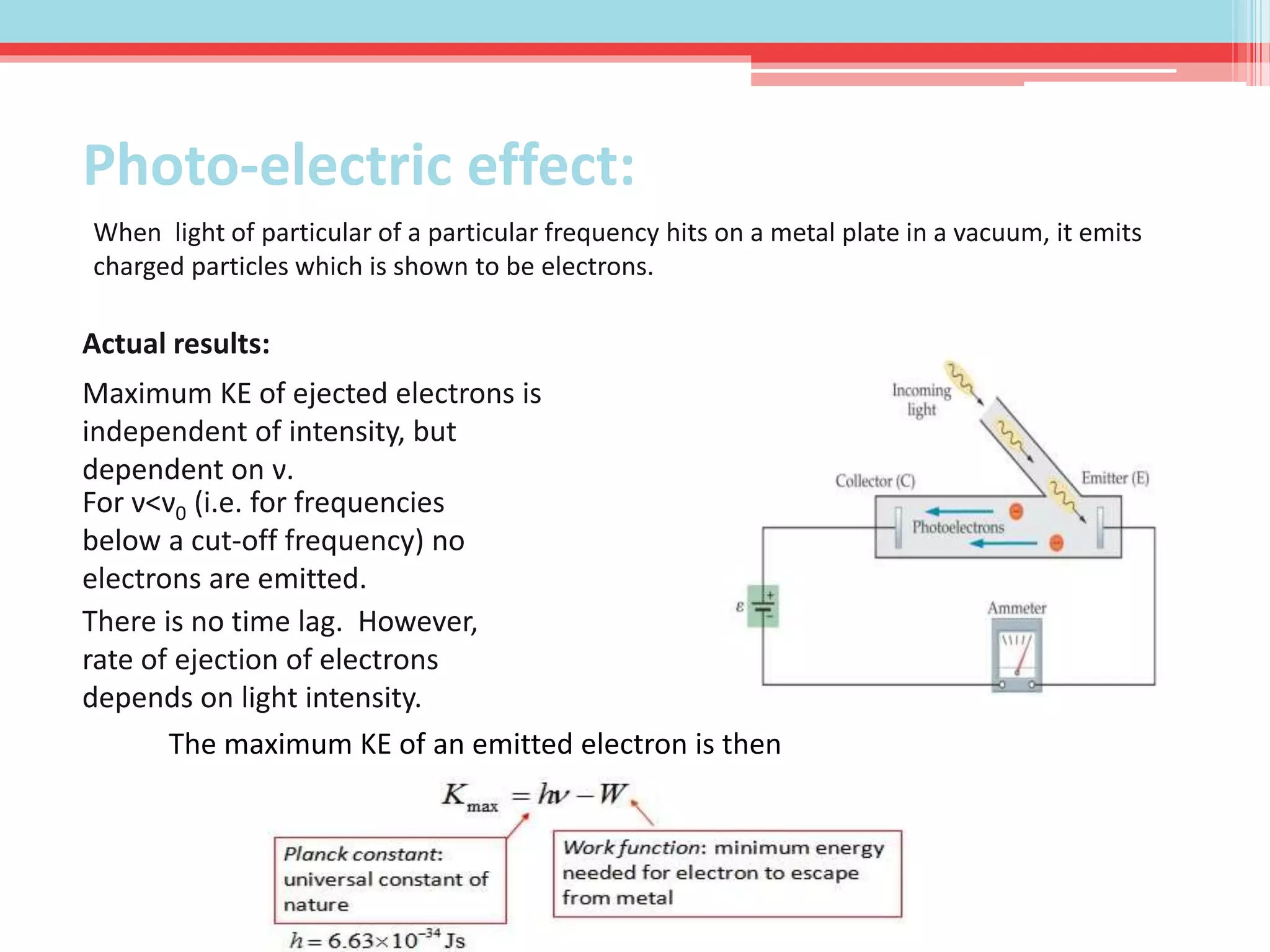
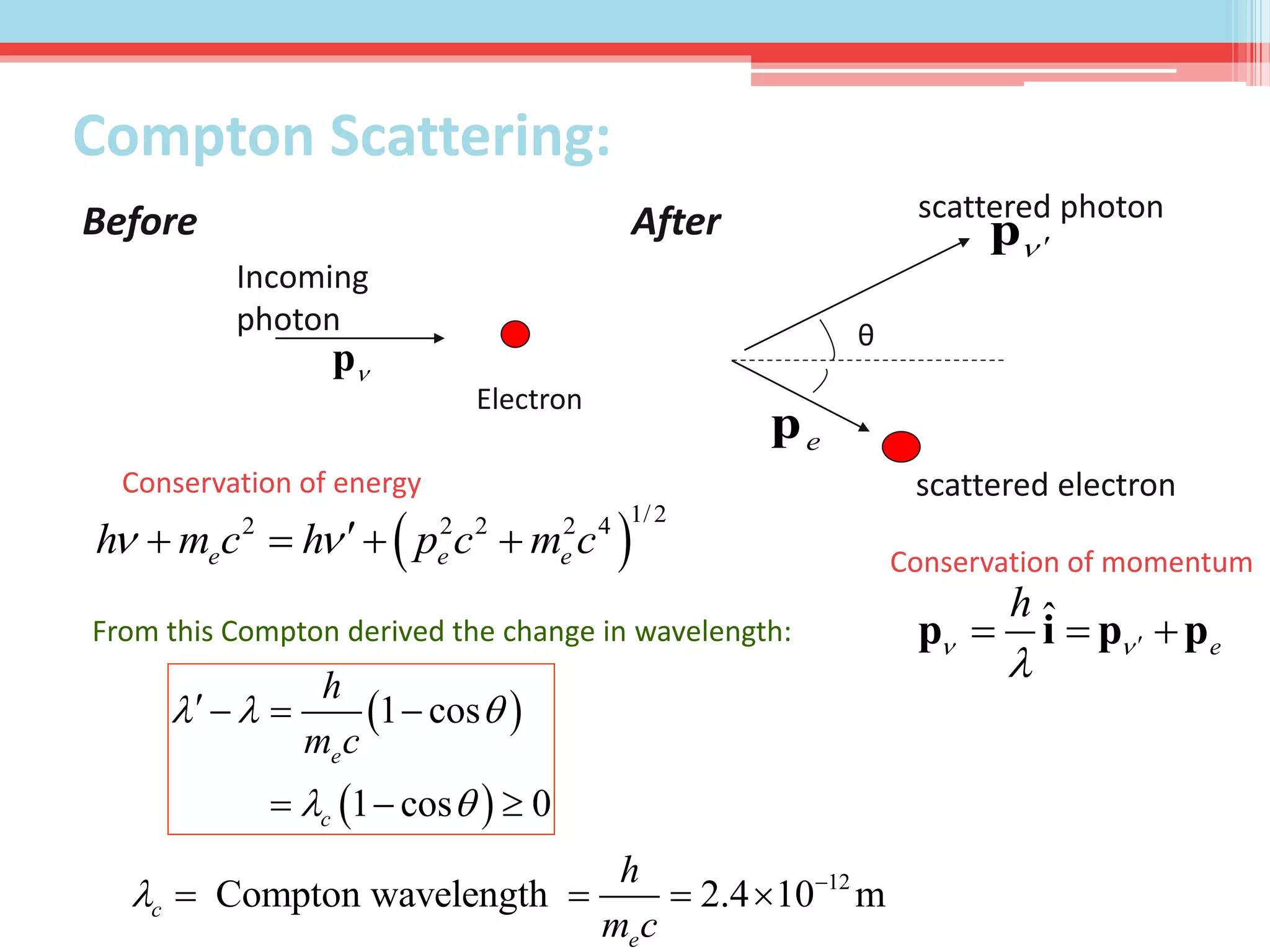
This document summarizes Louis de Broglie's hypothesis of wave-particle duality and its applications. It discusses de Broglie's proposal that particles have wave-like properties with a wavelength given by Planck's constant divided by momentum. The photoelectric effect and Compton effect provide evidence of wave and particle behavior of light and electrons. Wave-particle duality is exploited in technologies like electron microscopy and neutron diffraction to examine structures smaller than visible light wavelengths. While useful, wave-particle duality does not fully explain quantum phenomena like the Heisenberg uncertainty principle.

1. EAST WEST UNIVERSITY
Group Member:
Sudeb Das
ID:2014-2-55-023
Susmita Sarkar
ID:
Ayan Chowdhury
ID:2016-1-50-016
Presentation:
De Broglie Hypothesis

2. Background
The non-particle behavior of matter was first
proposed in 1923, by Louis de Broglie, a French
physicist.
In his PhD thesis, he proposed that particles also
have wave-like properties.
 Although he did not have the ability to test this
hypothesis at the time, he derived an equation to
prove it using Einstein's famous mass-energy relation
and the Planck equation.

3. Introduction
De Broglie Hypothesis:
In quantum mechanics, any object can behave both like wave-
particle duality at the sub-microscopic level.
Wave-particle Duality:
An object can act as both wave and particle at a same time. This
phenomenon is called wave-particle duality.
So, the object would have energy packets, momentum(can be
passed to another object), wave length, frequency and
amplitude etc.
By using photo-electric effect and Compton effect
we can easily describe about the wave particle duality

4. A beam of light can be treated as a stream of particles (PHOTONS) with zero
rest mass
Each photon has energy:

hc
hfEp 
where h is a constant (Planck’s constant, h ≈ 6.63 x 10-34 Js)
f, λ, c, are frequency, wavelength and velocity of light (in vacuum) respectively.
Light intensity is proportional to PHOTON FLUX (no of photons passing
through unit area per second)
Einstein’s Postulate

5.    2222
pcmcE 
consequently, particle with zero rest mass (eg photon) has momentum p
given by:

h
c
hf
c
E
p 
From Special Theory of Relativity

6. Photo-electric effect:
When light of particular of a particular frequency hits on a metal plate in a vacuum, it emits
charged particles which is shown to be electrons.
Actual results:
Maximum KE of ejected electrons is
independent of intensity, but
dependent on ν.
For ν<ν0 (i.e. for frequencies
below a cut-off frequency) no
electrons are emitted.
There is no time lag. However,
rate of ejection of electrons
depends on light intensity.
The maximum KE of an emitted electron is then

7. E h
h h
p
c


 
E  h p k h
2
h

h
2
k



Energy and frequency
Also have relation between momentum and wavelength
2 2 2 2 4
E p c m c 
c 
Relation between particle and wave properties of light
Relativistic formula relating
energy and momentum
E pcFor light and
Also commonly write these as
2 
angular frequency
Wave vector
hbar
Summary of Photon Properties

8. Compton (1923) measured intensity of scattered X-rays from solid target, as function of
wavelength for different angles.
Result: peak in scattered radiation shifts to longer wavelength than source. Amount
depends on θ (but not on the target material).
Compton Effect

9. Conservation of energy
Conservation of momentum 
1/22 2 2 2 4
e e eh m c h p c m c    
ˆ
e
h
 

  p i p p
 
 
1 cos
1 cos 0
e
c
h
m c
  
 
  
  
12
Compton wavelength 2.4 10 mc
e
h
m c
 
   
From this Compton derived the change in wavelength:
θ
ep
 pBefore After
Electron
Incoming
photon
p
scattered photon
scattered electron
Compton Scattering:

10. Note that, at all angles
there is also an unshifted peak.
This comes from a collision between the X-ray
photon and the nucleus of the atom
 1 cos 0
N
h
m c
     :
N em m?since
>
>
Compton Scattering:

11. Application
• Although it is difficult to draw a line separating wave–particle
duality from the rest of quantum mechanics, it is nevertheless
possible to list some applications of this basic idea.
• Wave–particle duality is exploited in electron microscopy, where
the small wavelengths associated with the electron can be used to
view objects much smaller than what is visible using visible light.
• Similarly, neutron diffraction uses neutrons with a wavelength of
about 0.1 nm, the typical spacing of atoms in a solid, to determine
the structure of solids.
• Photos are now able to show this dual nature, which may lead to
new ways of examining and recording this behavior.

12. Conclusion
From the discussion we can come to a decision that a particle can exhibit
wave particle duality and de Broglie has given the relation which is E=hv and
p=
But it has some limit. A central concept of quantum mechanics,
duality addresses the inadequacy of conventional concepts like "particle" and
"wave" to meaningfully describe the behavior of quantum objects. Since. it
cannot explain the Heisenberg uncertainty.