Application of derivatives

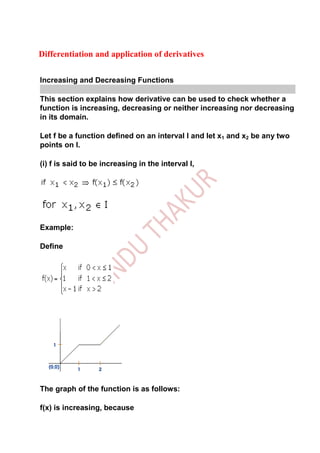
Differentiation and application of derivatives

Increasing and Decreasing Functions

This section explains how derivative can be used to check whether a
function is increasing, decreasing or neither increasing nor decreasing
in its domain.

Let f be a function defined on an interval I and let x1 and x2 be any two
points on I.

(i) f is said to be increasing in the interval I,

Example:

Define

The graph of the function is as follows:

f(x) is increasing, because

Since 2 - 1 < 3 - 1

(ii) f is said to strictly increasing in the interval I if

For example,

Let x1 < x2

f(x) is strictly increasing function.

(iii) f(x) is said to be decreasing function if for x1, x2 I

For example,

f(x) = 1 - x for 0 < x < 1

= 0 for 0 x <2

= 2 - x for x 2

is a decreasing function.

(iv) f (x) is said to be strictly decreasing on an interval I if for

For example,

is strictly decreasing function.

Theorem 1:

Let f be continuous on [a, b] and differentiable on the open interval (a,
b). Then

(a) f is increasing on [a, b] if f '(x) > 0 for each x (a, b)

(b) f is decreasing on [a, b] if f '(x) < 0 for each x (a, b)

This theorem can be proved by using Mean Value Theorem. We shall

prove the theorem after learning Mean Value Theorem.

This theorem is applied in various problems to check whether a
function is increasing or decreasing.

Working Rule to Check Whether a Differentable Function is Increasing
or Decresing

(1) Let the given function be f (x) on the real number line R.

(2) Differentiate the function f(x) with respect to x and equate it to zero
i.e., put f '(x) = 0. Solve for x. These values of x which satisfy f '(x) = 0
are called Critical values of the function

(3) Arrange these Critical values in ascending order and partition the
domain of f (x) into various intervals, using the Critical values.

(4) Check the sign of f '(x) in each open intervals.

(5) If f '(x) > 0 in a particular interval, then the function is increasing in
that particular interval.

If f '(x) < 0 in a particular interval, then the function is decreasing in
that particular interval.

Example:

Find the intervals on which the function

(a) increasing (b) decreasing

Differentiating the function, we have

The critical values in ascending order are -1, 1. We divide the Real

numbers into the intervals

= - ve

Since f '(x) < 0, the function is decreasing in the interval .

Since f '(x) > 0 in the interval (-1, 1), the function is increasing in this
interval.

= - ve

Since f '(x) < 0, f(x) is decreasing in the interval (1, )

Maxima and Minima

A function f(x) is said to have a local maximum at x = a, if is a
neighbourhood I of 'a', such that

f(a) f(x) for all x I

The number f(a) is called the local maximum of f(x). The point a is called
the point of maximum.

Note that when 'a' is the point of local maxima, f(x) is increasing for all
values of x < a and f (x) is decreasing for all values of x > a in the given
interval.

At x = a, the function ceases to increase.

A function f(x) is said to have a local minimum at x = a, if is a
neighbourhood I of 'a', such that

f(a) f(x) for all x I

Here, f(a) is called the local minimum of f(x). The point a is called the
point of minimum.

Note that, when a is a point of local minimum f (x) is decreasing for all x
< a and f (x) is increasing for all x > a in the given interval. At x = a, the
function ceases to decrease.

If f(a) is either a maximum value or a minimum value of f in an interval I,
then f is said to have an extreme value in I and the point a is called the
extreme point.

Monotonic Function

A function is said to be monotonic if it is either increasing or decreasing
but not both in a given interval.

Consider the function

The given function is increasing function on R. Therefore it is a
monotonic function in [0,1]. It has its minimum value at x = 0 which is
equal to f (0) =1, has a maximum value at x = 1, which is equal to f (1) =
4.

Here we state a more general result that, 'Every monotonic function
assumes its maximum or minimum values at the end points of its
domain of definition.'

Note that 'every continuous function on a closed interval has a
maximum and a minimum value.'

Theorem 2:
(First Derivative Test)

Let f (x) be a real valued differentiable function. Let a be a point on an
interval I such that f '(a) = 0.

(a) a is a local maxima of the function f (x) if

i) f (a) = 0

ii) f (x) changes sign from positive to negative as x increases through a.

That is, f (x) > 0 for x < a and

f (x) < 0 for x > a

(b) a is a point of local minima of the function f (x) if

i) f (a) = 0

ii) f (x) changes sign from negative to positive as x increases through a.

That is, f (x) < 0 for x < a

f (x) > 0 for x > a

Working Rule for Finding Extremum Values Using First Derivative Test

Let f (x) be the real valued differentiable function.

Step 1: Find f '(x)

Step 2: Solve f '(x) = 0 to get the critical values for f (x). Let these values
be a, b, c. These are the points of maxima or minima.
Arrange these values in ascending order.

Step 3: Check the sign of f'(x) in the immediate neighbourhood of each
critical value.

Step 4: Let us take the critical value x= a. Find the sign of f '(x) for
values of x slightly less than a and for values slightly
greater than a.

(i) If the sign of f '(x) changes from positive to negative as x increases
through a, then f (a) is a local maximum value.

(ii) If the sign of f '(x) changes from negative to positive as x increases
through a, then f (a) is local minimum value.

(iii) If the sign of f (x) does not change as x increases through a, then f
(a) is neither a local maximum value not a minimum value. In this case x
= a is called a point of inflection.

Example:

Find the local maxima or local minima, if any, for the following function
using first derivative test

f (x) = x3 - 6x2 + 9x + 15

Solution:

f (x) = x3 - 6x2 + 9x + 15

f ' (x) = 3x2 -12x + 9

= 3(x2- 4x + 3)

= 3 (x - 1) (x - 3)

Thus x = 1 and x = 3 are the only points which could be the points of
local maxima or local minima.

Let us examine for x=1

When x<1 (slightly less than 1)

f '(x) = 3 (x - 1) (x - 3)

= (+ ve) (- ve) (- ve)

= + ve

When x >1 (slightly greater than 1)

f '(x) = 3 (x -1) (x - 3)

= (+ ve) (+ ve) (- ve)

= - ve

The sign of f '(x) changes from +ve to -ve as x increases through 1.

x = 1 is a point of local maxima and

f (1) = 13 - 6 (1)2 + 9 (1) +15

= 1- 6 + 9 + 15 =19 is local maximum value.

Similarly, it can be examined that f '(x) changes its sign from negative to
positive as x increases through the point x = 3.

 x = 3 is a point of minima and the minimum value is

f (3) = (3)3- 6 (3)2+ 9(3) + 15

= 15

Theorem 3: (Second Derivative Test)
Let f be a differentiable function on an interval I and let a I. Let f "(a) be
continuous at a. Then

i) 'a' is a point of local maxima if f '(a) = 0 and f "(a) < 0

ii) 'a' is a point of local minima if f '(a) = 0 and f "(a) > 0

iii) The test fails if f '(a) = 0 and f "(a) = 0. In this case we have to go back
to the first derivative test to find whether 'a' is a point of maxima,
minima or a point of inflexion.

Working Rule to Determine the Local Extremum Using Second
Derivative Test

Step 1

For a differentiable function f (x), find f '(x). Equate it to zero. Solve the
equation f '(x) = 0 to get the Critical values of f (x).

Step 2

For a particular Critical value x = a, find f "'(a)

(i) If f ''(a) < 0 then f (x) has a local maxima at x = a and f (a) is the
maximum value.

(ii) If f ''(a) > 0 then f (x) has a local minima at x = a and f (a) is the
minimum value.

(iii) If f ''(a) = 0 or , the test fails and the first derivative test has to be
applied to study the nature of f(a).

Example:

Find the local maxima and local minima of the function f (x) = 2x3 - 21x2
+36x - 20. Find also the local maximum and local minimum values.

Solution:

f '(x) = 6x2 - 42x + 36

f '(x) = 0

x = 1 and x = 6 are the critical values

f ''(x) =12x - 42

If x =1, f ''(1) =12 - 42 = - 30 < 0

x =1 is a point of local maxima of f (x).

Maximum value = 2(1)3 - 21(1)2 + 36(1) - 20 = -3

If x = 6, f ''(6) = 72 - 42 = 30 > 0

x = 6 is a point of local minima of f (x)

Minimum value = 2(6)3 - 21 (6)2 + 36 (6)- 20

= -128

Absolute Maximum and Absolute Minimum Value of a Function

Let f (x) be a real valued function with its domain D.

(i) f(x) is said to have absolute maximum value at x = a if f(a)  f(x) for all
x  D.

(ii) f(x) is said to have absolute minimum value at x = a if f(a)  f(x) for all
x  D.

The following points are to be noted carefully with the help of the
diagram.

Let y = f (x) be the function defined on (a, b) in the graph.

(i) f (x) has local maximum values at

x = a1, a3, a5, a7

(ii) f (x) has local minimum values at

x = a2, a4, a6, a8

(iii) Note that, between two local maximum values, there is a local
minimum value and vice versa.

(iv) The absolute maximum value of the function is f(a7)and absolute
minimum value is f(a).

(v) A local minimum value may be greater than a local maximum value.

Clearly local minimum at a6 is greater than the local maximum at a1.

Theorem 4

Let f be a continuous function on an interval I = [a, b]. Then, f has the
absolute maximum value and f attains it at least once in I. Also, f has the
absolute minimum value and attains it at least once in I.

Theorem 5

Let f be a differentiable function on I and let x0 be any interior point of I.
Then

(a) If f attains its absolute maximum value at x0, then f ' (x0)= 0

(b) If f attains its absolute minimum value at x0, then f '(x0) = 0.

In view of the above theorems, we state the following rule for finding the
absolute maximum or absolute minimum values of a function in a given
interval.

Step 1: Find all the points where f ' takes the value zero.

Seep 2: Take the end points of the interval.

Step 3: At all the points calculate the values of f.

Step 4: Take the maximum and minimum values of f out of the values
calculated in step 3. These will be the absolute maximum or absolute
minimum values.

Rolle's Theorem and Mean Value Theorem
Rolle's Theorem

Let f be a real valued function in [a,b] such that

f is continuous in [a,b].

f is differentiable in (a,b).

Geometrical meaning

Let A (a,f (a)) and B (b,f (b)) be two points on the graph of f (x) such that f(a)
= f(b), then c  (a, b) such that the tangent at P(c, f(c)) is parallel to x -
axis.

Note 1: We cannot obtain c if any one of the conditions of Rolle's theorem
are not satisfied.

Note 2: The value of c need not be unique.

Example:

Verify Rolle's theorem for the function

f (x) = x2 - 8x + 12 on (2, 6)

Since a polynomial function is continuous and differentiable everywhere f
(x) is differentiable and continuous (i) and (ii) conditions of Rolle's theorem
is satisfied.

f (2) = 22 - 8 (2) + 12 = 0

f (6) = 36 - 48 + 12 = 0

Therefore (iii) condition is satisfied.

Rolle's theorem is applicable for the given function f (x).

 There must exist c (2, 6) such that f '(c) = 0

f '(x) = 2x - 8

Rolle's theorem is verified.

Working Rule for Verifying Rolle's Theorem

Let f (x) be a function defined on [a, b].

Step 1:

Show that the function is continuous in the given interval. Some known
standard functions which are continuous, can be mentioned directly.

Step 2:

Differentiate f (x) and examine if f '(x) is defined at every point in the open
interval (a, b).

Step 3:

Check if f (a) = f (b)

If all the above condition are satisfied, then Rolle's theorem is applicable
else the Rolle's theorem is not applicable.

Langrange's Mean Value Theorem
Theorem 7:

Let f be real valued function in [a,b] such that,

f is continuous in [a,b].

f is differentiable in (a,b).

Geometrical meaning

Let A (a,f (a)) and B (b,f (b)) be two points on f (x), then

Note: The value of c obtained need not be unique.

Working Rule to Verify Lagrange's Mean Value Theorem

(Mean Value Theorem)

Step 1:

Show the function f (x) is continuous on the closed interval [a, b].

Step 2:

Find f '(x) and examine if it is defined at every point on the open interval (a,
b). If f '(x) is defined for all x (a, b), then the function is differentiable.

Step 3:

If the above condition are satisfied, then Mean Value Theorem is applicable.

Step 4:

If Mean value theorem is applicable, solve the equation

Show that one of the roots lie in the open interval (a, b). This verifies the
Mean Value Theorem.

Example:

Verify mean value theorem for the function

f (x) = (x - 4) (x - 6) (x - 8) in [4,10]

Step1:

We know that every polynomial function is continuous and product of
continues functions are continuous. f (x), being product of polynomials of
degree 1, is a continuous function in [4,10].

Step 2:

f ' (x) = (x - 6) (x - 4) + (x - 4) (x - 8) + (x - 6) (x - 8)

f '(x)= (x2 -10x + 24) + (x2 - 12x + 32)+ (x2 - 14x + 48)

= 3x2 - 36x + 104

f '(x) is defined for all values on the interval (4,10).

 f '(x) is differentiable.

Step 3:

Since both the condition are satisfied, Mean Value Theorem is applicable.

There exist c (4, 10) such that

 f (4) = 0

f '(c) = 3c2 - 36c + 104

Substituting these values in (1), we have

Since 8 (4,10), Mean Value Theorem is satisfied.
Approximations by Differentials

Let y = f (x) be a differentiable function of x, errors in x and y are
denoted by x and y, we have

 Error in y = f ' (x) x.

Note 1:

Note 2:

Note 3:

y and dy are not usually the same and dy is the approximate value
of y.

Note 4: dx and dy are called the differentials of x and y respectively.

Example:

Find the approximate value of fourth root of 82 upto 3 decimal
places.

Solution:

Let y = f (x) = x1/4

Let x = 81, x =1. Taking these values we have

Rate of Change of Quantity

If a quantity y varies with respect to another quantity 'x'
satisfying some rule y = f(x), in other words if y is a function

x, then

represents the rate of change of y with respect to x

For x = x0,

dy/dx at x0 is called the rate of change of y with respect to x
at x0.

If y is a function of t

x is a function of t

That is if x = f (t) and y = g(t)

We know that

The rate of change of y with respect to x in this case, can be
found by finding out the rate of change of y with respect to t
and that of x with respect to t.

Example:

A balloon which always remain spherical is being inflated by
pumping in 900 cubic centimetres of gas per second. Final
the rate at which the radius of the balloon increasing when
the radius is 15cm.

Let r and V be the variables for radius and volume of the
balloon respectively.

We have to find

For a sphere

Differentiating both sides with respect to t, we have

Tangents and Normals

Note 1: If m = 0 the tangent is parallel to x-axis.

Note 3: Equation of the tangent at (x1,y1) is

or

Note 4: Equation of the normal at (x1,y1) is

or

Example:

Find the equation of the tangent to the curve which is
parallel to the line 4x - 2y + 5 = 0.

Solution:

Since the tangent to the given curve is parallel to the line

4x - 2y + 5 = 0

Slope of the tangent = Slope of the given line

On simplification, the equation is 48 x - 24y = 23.

Curve Sketching

The graph of a given function gives a visual presentation of the
behaviour of the function involving a study of symmetry, rise and
fall, region of existence, passage through specific points etc.

The following points are helpful to trace the curve.

Symmetry

a) Symmetry about x - axis

If the equation of the curve remains unaltered when y is replaced
by -y, then the curve is symmetrical about x-axis.

b) Symmetry about y-axis

If the equation of the curve remains unaltered when x is replaced
by -x then the curve is symmetrical about y-axis.

c) Symmetry about y = x

If the equation of the curve remains unaltered if x and y are
interchanged, then the curve is symmetrical about y = x.

d) Symmetry about y = -x

If x and y are replaced by -y and -x and the equation of the curve is
unaltered, then the curve is symmetrical about the line y = -x.

e) Symmetry in opposite quadrants

If the equation of the curve is unaltered, when x and y are replaced

by -x and -y, then it is symmetrical in opposite quadrants.

Example:

Sketch the curve

y = - sin 2x ….(1)

Solution:

Symmetry

(a) By replacing y by -y, the equation (1) is altered, therefore the
curve is not symmetrical about x-axis.

(b) By replacing x by -x, the equation of the curve is altered,
therefore the curve is not symmetrical about y-axis.

(c) Replace x and y by -x and -y respectively in the equation y = -
sin 2x, the equation of the curve remain unaltered. Therefore the
curve is symmetrical in opposite quadrants.

Passage through origin

Put x = 0, y = -sin2x = 0. This implies (0, 0) is a point on the curve or
the curve passes through the origin.

Points of intersection

The points of intersection with x-axis is determined by letting y = 0.

Putting y = 0, - sin 2x = 0

This implies the curve intersects the x-axis at the points where

The points at which the tangent is parallel to x-axes are determined
by solving.

y = - sin 2x

The tangent is parallel to x- axis at

We know that sin x is a periodic function with 2, that is

sin(2 + x) = sinx

The pattern of the curves repeats at an interval .

Therefore it is sufficient to sketch the curve form 0 to .

Determination of Few Point

with this information, we sketch the graph as show .

Summary

Let y = f(x) be a smooth curve and P(x,y) be a point on the curve.

Equation of the tangent at (x1, y1) in the curve y = f (x) is

y - y1

Equation of the normal at (x1, y1) in the curve y = f (x) is

If m = 0 the tangent at (x1, y1) is parallel to x-axis.

Angle of intersection of the curves is the acute angle between
their tangents at the point of intersection.

Let y = f1(x) and y = f2(x) be two curves intersecting at P.

If m1 = m2 the curves touch each other.

If m1m2 = -1 the curves are orthogonal.

The condition for the function f(x) to be increasing at x = a if

f'(a) >0.

The condition for f(x) to be decreasing at x = a if f'(a) < 0.

A function f(x) is said to be strictly increasing at x = a if f(x) > f(a)
whenever x > a in the neighbour hood of a.

A function f(x) is said to be strictly decreasing at x = a if f(x) < f(a)
whenever x>a in the neighbour hood of a

If f'(a) = 0 then x = a is called a stationary point.

If f'(a)=0, x=a is called the stationary point and the tangent at
(a,f(a)) is parallel to x - axis.

A function f(x) is said to have a maximum at x = a if

The conditions for y = f(x) to have a maximum at x = a are

A function f(x) is said to have a minimum at x = a

The conditions for y = f(x) to have a minimum at x = a are

x = a is called a point of inflexion.

Rolle's theorem: If a function f(x) is such that

(i) f (x) is continuous on [a,b]

(ii) f (x) is differentiable on (a,b) and

(iii) f (a) = f (b)

Geometrical interpretation of Rolle's theorem

Let AB be the graph of y = f(x) such that A = (a,f(a)) and B = (b,f(b))

(i) f (x) is continuous between A and B.

(ii) f (x) has derivative between A and B i.e., there is a unqiue
tangent at every point between A and B.

(iii) f (a) = f(b)

at C is parallel to x-axis.

Langrange's Mean Value theorem: If a function f (x) is such that

(i) f (x) is continuous on [a,b] and

(ii) f (x) is differentiable on (a,b) then

Geometrical interpretation of Lagrange's Mean value theorem.

Let A(a, f(a)) and B(b, f(b)) be two points on the curve y = f (x) such
that

(i) f (x) is continuous between A and B.

(ii) f (x) is differentiable between A and B

i.e., there is a unique tangent at every point between A and B.

then there exists a point C(c, f(c)) between A and B such that the
tangent at C is parallel to the chord AB.

Note that the point C is not unique.

Relation between y and dy

Let A(x, y) and B(x + x, y + y) be two neighbouring points on the
curve y = f(x).

Let dx and dy be the differentiables of x and y respectively.

AC = x = dx

BC = y

DC = dy

dy = f'(x)x

y - dy = BC - CD = BD

 The differential 'dy' and the increment 'y' may not be equal.

Generally the following points are examined for tracing the
curves

(i) Symmetry about x - axis

(ii) Symmetry about y - axis

(iii) Symmetry in opposite quadrants

(iv) Symmetry about the line y = x

(v) Passage through specific points

(vi) Points of intersection with the axes

(vii) Regions where the curve is increasing or decreasing

(viii) Region of existence.

PROBLEMS

To find the equation of the tangent line of

First, we find the derivative:

The equation of the tangent line is:







y - 0.333 = -0.667 (x - 0.5)




y - 1 = -1 (x - 1)

Problem:
Find the inverse of

Solution:
Frist, we differentiate

The derivative of f -1 is:

The tangent line at (-1, 0) is:

Problem:
Find the inverse of

Solution:
Frist, we differentiate

The derivative of f -1 is:

The tangent line at (7, 1) is:

Problem:
Using logarithmic differentiation, differentiate:

Solution:

Problem:

Solution:

Problem:

Solution:

Problem: Using differentials, approximate the expression

Solution:

We let

Hence,

x = 2 and y = 5.

Differentiating, we obtain

Substituting, we get

**Problem: Using differentials, approximate the expression

Solution:

We let

Hence,

x = -.0015926... and y = 0.




Solution:

We let

Hence,

x = .035398... and y = 1.




Solution:

We let

Hence,

x = 0.05 and y = 0.




Solution:

We let

Hence,

x = -0.1 and y = 9.




Solution:

We let

Hence,

x = 0.05 and y = /4.



To find the absolute maxima and minima of the function

we first take the derivative

and find the roots of the derivative which are:

x = 0.63486... and x = 2.50672....

These are the only critical points of f. We consider the following table of
the endpoints and the critical points of f:

x f(x)
0 1
3.14159... -1
0.63486... 1.76017...
2.50672... -1.76017...

from which we see that the absolute maximum occurs at x = 0.63486... and
is 1.76017... and the absolute minimum occurs at x = 2.50672... and is -
1.76017... .



and find the roots of the derivative which are:

x = -2 and x = 0.

These are the only critical points of f. We consider the following table of
the endpoints and the critical points of f:

x f(x)

-5 0.16844...
1 2.71828...
-2 0.54134...
0 0

from which we see that the absolute maximum occurs at x = 1 and is
2.71828... and the absolute minimum occurs at x = 0 and is 0.



and find the root of the derivative which is:

x = -1.

This is the only critical point of f. We consider the following table of the
endpoints and the critical points of f:

x f(x)
-4 2.48490...
3 2.94443...
-1 1.09861...

from which we see that the absolute maximum occurs at x = 3 and is
2.94443... and the absolute minimum occurs at x = -1 and is 1.09861... .

Problem: Using L'Hospital's Rule, evaluate the limit

Solution:
Since

we can apply L'Hospital's Rule:


Solution:
Since



Solution:
Since


To apply L'Hospital's Rule again, we need to check:


Solution:
Since



Solution:
Since


To apply L'Hospital's Rule again, we need to check:

To apply the Mean Value Theorem to the function

we first calculate the quotient

Next, we take the derivative

and equate it to the result of the calculation above:

We solve this equation to get two answers:

x = 0.7704383989 and x = 2.371154255.

**To apply the Mean Value Theorem to the function




We solve this equation to get

x = -0.9012084345.

**To apply the Mean Value Theorem to the function




We solve this equation to get three answers:

x = 1.109744819, x = 2.403237586 and 4.022404459.

 We are given the function

 First, we find the derivative:

 We set the derivative equal to 0 and solve:

 Since the domain of f is the same as the domain of f', -2 and 0 are the
only critical numbers of f.
 Testing:

x < -2 f'(-10) = 80 e- 10 f is increasing
-2 < x < 0 f(-1) = - e- 1 f is decreasing
x>0 f(1) = 3 e f is increasing

 By the First Derivative Test, x = - 2 is a local minimum and x = 0 is a
local maximum.




 Since f' is not defined at - 3 and 3 which are in the domain of f, -3, 0
and 3 are the critical numbers of f.
 Testing:

x < -3 f'(-10) = -20 f is decreasing
-3 < x < 0 f(-1) = 2 f is increasing
0<x<3 f(1) = -2 f is decreasing
x>3 f(10) = 20 f is increasing

 By the First Derivative Test, x = -3 and x = 3 are local minima and x =
0 is a local maximum.




 Since the domain of f is the same as the domain of f', 0 is the only
critical number of f.
 Testing:

x < 0 f'(-1) = -1 f is decreasing
x>0 f'(1) = 1 f is increasing

 By the First Derivative Test, x = 0 is a local minimum.


 First, we find the first and second derivatives:

 Clearly, there is no solution for f''(x) = 0.
 Note that - 3 and 3 are in the domain of f but are not in the the domain
of f''; hence, x = -3 and x = 3 are the only possible candidates for
inflection points.
 Testing:

x < -3 f''(-5) = 2 f is concave upward
-3 < x < 3 f''(0) = -2 f is concave downward
x>3 f''(1) = 2 f is concave upward

 Therefore, x = -3 and x = 3 are inflection points.



 We set the second derivative equal to 0 and solve:

 Since the domain of f is the same as the domain of f'', x = -3.41.. and x
= -0.58.. are the only possible candidates for inflection points.
 Testing:

x < -3.41.. f''(-4) = 0.036.. f is concave upward
-3.41.. < x < -0.58.. f''(-1) = -0.36.. f is concave downward
x > -0.58.. f''(0) = 2 f is concave upward

 Therefore, x = -3.41.. and x = -0.58.. are inflection points.



 Clearly, there is no solution for f''(x) = 0.
 Note that the domain of f is [ 0, 4 ] and the domain of f'' is ( 0, 4 );
hence, there are no inflection points.
 Testing:

0 < x < 4 f''(1) = -0.769.. f is concave downward

( Ncert) Ex.6.1

qQuestion 2:The volume of a cube is increasing at the rate of 8 cm3/sec.
HHow fast is the surface area increasing when the length of an edge is
12 cm?

Answer 2: V= X3 ( x is a side) , S = 6X2 ⇨ dv/dt (8 cm3/s)= 3x2.dx/dt

Put dx/dt in dS/dt = 32/x cm2/sec, at x=12 cm will be 8/3 cm2/sec.

Question 4: An edge of a variable cube is increasing at the rate of 3
cm/s. How fast is the volume of the cube increasing when the edge is
10 cm long?

Answer 4: V= x3 , Rate of change in volume = dV/dt, , at x=10 is 900
cm3/sec. (∵ dx/dt=3 cm.)

Question 5:A stone is dropped into a quiet lake and waves move in
circles at the speed of 5 cm/s. At the instant when the radius of the
circular wave is 8 cm, how fast is the enclosed area increasing?
Answer 5: A= r2 , dr/dt =5cm/sec. , dA/dt= 10 r=80 cm2/sec.(r=8)

Question 7:The length x of a rectangle is decreasing at the rate of 5
cm/minute and the width y is increasing at the rate of 4 cm/minute.
When x = 8 cm and y = 6 cm, find the rates of change of (a) the
perimeter, and (b) the area of the rectangle.

Answer 7:(same as example)(a) dP/dt=2cm/min.(perimeter decreases)

(b) dA/dt=2cm2/min.(shows area increases).
Question 8:A balloon, which always remains spherical on inflation, is
being inflated by pumping in 900 cubic centimetres of gas per second.
Find the rate at which the radius of the balloon increases when the
radius is 15 cm.
Answer 8: V=4/3 r3 , dV/dt=900=4 r2dr/dt at r=15⇨ dr/dt=7/22
Question 10:A ladder 5 m long is leaning against a wall. The bottom of
the ladder is pulled along the ground, away from the wall, at the rate
of 2 cm/s. How fast is its height on the wall decreasing when the foot
of the ladder is 4 m away from the wall?

Answer 10: AB is ladder(hyp.)OA=4=x(base), OB=y(per.) so x2+y2=25
Y=3(by pytha.) diff. W.r.t. t ⇨ dx/dt=.02m/sec. & dy/dt=-2/75(dec.)
Question 13:A balloon, which always remains spherical, has a variable

diameter Find the rate of change of its volume with respect
to x. [Ans. dv/dx= 27 /8(2x+1)2 ]
Question 14:Sand is pouring from a pipe at the rate of 12 cm3/s. The
falling sand forms a cone on the ground in such a way that the height
of the cone is always one-sixth of the radius of the base. How fast is
the height of the sand cone increasing when
Answer 14: put r=6h in Volume gives 12 h3 ⇨ dV/dt= 12 cm3/s. ⇨
dh/dt= 1/(3 h2) =1/48 at h=4cm.
Question 16:The total revenue in Rupees received from the sale of x
units of a product is given by

Find the marginal revenue when x = 7.

Answer 16: Marginal Revenue(MR) = dR/dx, at x=7 is Rs. 208.

EX. 6.2 Question 5: Find the intervals in which the function f given by

f(x)= 2x3 – 3x2 – 36x+7 is strictly increasing or decreasing.

Answer 5: f is strictly ↑ if f’(x)>0 & strictly ↓ or f is strictly increasing on
(-∞, -2)U(3, ∞) and decreasing on (-2, 3)
Question 6:Find the intervals in which the following functions are
strictly increasing or decreasing: (a) x2 + 2x − 5 (b) 10 − 6x − 2x2

(c) −2x3 − 9x2 − 12x + 1 (d) 6 − 9x − x2 (e) (x + 1)3 (x − 3)3

Answer 6: (a) f is strictly increasing on (-1, ∞) and decreasing on (-∞, -
1) (b) f is strictly increasing on (-∞, -3/2) and decreasing on (-3/2, ∞)
(c) f is strictly increasing on -2<x<-1 and decreasing on x<-2 & x>-1.(d) f
is strictly increasing for x<-9/2 and decreasing for x>-9/2. (e) f’(x)=
6(x+1)2(x-3)2(x-1) > & <0 for ↑ & ↓ , f is ↑ on (1, ∞) & ↓ on (-∞,1),(-1,1)

Question 7:Show that , is an increasing
function of x throughout its domain.
Answer 7: f’(x) = > 0 ⇨ f is increasing function of x ∀ x>-1

Question 9: Prove that is an increasing function

of θ in .
Answer 9: dy/dx= > 0 ⇨ cosѲ >0,[ )>0 as cos2Ѳ
Is not >1] ∴ Ѳ ∊ (0, п/2)
Question 11:Prove that the function f given by f(x) = x2 − x + 1 is
neither strictly increasing nor strictly decreasing on (−1, 1).
Answer 11: f’(x)=2(x-1/2), -1<x<1/2 ⇨ (x-1/2)<0⇨ f’(x)<0 and ½<x<1
⇨ x-1/2>0 i.e., f’(x)>0, f’(X) does’nt have same sign in interval (-1,1).
Question 12:Which of the following functions are strictly decreasing

on ? (A) cos x (B) cos 2x (C) cos 3x (D) tan x
Ans. 12: A,B are ↓ on (o, п/2) , (C) is neither ↑ nor ↓ on (D) ↑ on (o, п/2)
Question 13:On which of the following intervals is the function f given
by strictly decreasing?

(A) (B) (C) (D) None of these

Answer 13: f’(x) =100x99+cosx (A) 1 radian = 570 ∴ x∊ (0,1) means x lies
in 1st quad. ∴ cosx >0⇨ 100x99+cosx>0 ⇨ f is ↑ . (B) п/2<x<п ⇨
22/14<x<22/7 means 100x99 >100 & п/2<x<п ⇨ -1< cosx<0 or
0>cosx>-1 ∴ 100x99+cosx > 100-1=99 ⇨ f is ↑. (C) f is ↑ (D) is correct.
Question 14:Find the least value of a such that the function f given

is strictly increasing on (1, 2).
Answer 14: f’(x) = 2x+a , for f to be ↑ on [1,2], f’(x) should be +ve in
[1,2]. At the end point x=1 2x+a=2+a which is +ve or zero i.e., 2+a≥0

At the end point x=2 2x+a=4+a which is +ve or zero i.e., 4+a≥0 if a≥-4
∴ from above results we obtain the least value of a = -2.
Question 15:Let I be any interval disjoint from (−1, 1). Prove that the

function f given by is strictly increasing on I.
Answer 15: f’(x) = ≥ 0 , is ↑ ∵ x2≥1≥0 , f is strictly increasing on I.
Question 16:Prove that the function f given by f(x) = log sin x is strictly

increasing on and strictly decreasing on

Answer 16: f’(x) = cotx , f is ↑ on & ↓ on as f’ is +ve & -ve.
Question 17:Prove that the function f given by f(x) = log cos x is strictly

decreasing on and strictly increasing on
EXTRA questions

Ques. 1 Determine the value of x for which f(x) = xx , x>0 is increasing
or decreasing.
xlogx
Answer: Domain f =(0,∞) , f’(x) = e d/dx(xlogx)= xx (1+logex)

For ↑ 1+logex>0 as xx >0 for x>0 ⇨ logex >-1 ⇨ x> e-1 , x∊ (1/e, ∞)

Similarly f is ↓ on (0, 1/e)

Ques. 2Find the intervals in which f(x) = sinx – cosx, 0< x< 2п, is strictly
increasing or strictly decreasing .

Answer: f’(x) = cosx+sinx= √2(1/√2 sinx + 1/√2 cosx)= √2 sin(x+п/4)

0<x<2п ⇨ п/4<x+п/4<9п/4 ,we know that sin(x+п/4)>0 for
п/4<x+п/4<п or 2п<x+п/4<9п/4 ⇨ sin(x+п/4)>0 for 0<x <3п/4 or
7п/4<x<2п ⇨ f is strictly ↑ in (0,3п/4)U(7п/4,2п) & ↓ in [3п/4,7п/4]

Question 3: Find local max. & mini. Value of f(x) =sin4x + cos4x,

x∊(0,п/2) . *Answer: f’(x)=0⇨-sin4x =0 ⇨ x=п/4, put f’’(x)>0, local mini.
Value is ½]

Question 4: Shoe that the rectangle of max. Area that can be inscribed
in a circle of radius r is a square of side √2r.

Answer: r be radius , Ѳ be the angle b/w side of rectangle & diameter

A= 2rcosѲ.2rsinѲ, dA/dѲ=0 ⇨ cos2Ѳ=0 ⇨ Ѳ=п/4, show 2nd der. <0

Sides are √2r,so it becomes square has max. Area.

EX.6.3 Question 9:Find the point on the curve y = x3 − 11x + 5 at which
the tangent is y = x − 11.

Answer 9: dy/dx = 3x2-11 , slope of tangent (m)=1, after solving x=∓2

⇨y=-13,-9 ,so(2,-9) will be the point ∵ (-2,-13) does not lie on curve.

Question 13: Find points on the curve at which the tangents
are (i) parallel to x-axis (ii) parallel to y-axis

Answer 13: dy/dx = -16x/9y (i) dy/dx=0⇨x=0 ∴y=∓4 (ii) dy/dx=∞⇨y=0
Question 15: Find the equation of the tangent line to the
curve y = x2 − 2x + 7 which is (a) parallel to the line 2x − y + 9 = 0

(b) perpendicular to the line 5y − 15x = 13.

Answer 15: dy/dx=2(x-1) (a) dy/dx = m= 2⇨ x=2 & y=7, eqn. Is 2x-y+3=0

(b) dy/dx=m=3, but it is per. ∴ 2(x-1) = -1/3⇨x=5/6 & y=217/36, then eqn.

(y-y1 ) = m(x-x1) ( by point slope form) gives 12x+36y – 227=0.

Question 18: For the curve y = 4x3 − 2x5, find all the points at which
the tangents passes through the origin.

Answer 18: Let (h,k) be the point on curve then k = 4h3 – 2h5 .......(i)
Dy/dx = 12h2 – 10h4 at (h,k), eqn. Of tangent at (h,k) is
Y – k = (4h3 – 2h5 ) (x-h), it passes through origin⇨ k=12h3-10h5 , solve
with (i) ⇨ h=0 or ∓1 ⇨ k=0,-2,2
Question 21: Find the equation of the normal to the curve y = x3 + 2x + 6
which are parallel to the line x + 14y + 4 = 0.
Answer 21: dy/dx= 3x2+2 , dy/dx=m(of line)= -1/14 , but normal to the
curve parallel to line ⇨ (-dx/dy)(x1,y1) = -1/14⇨ x1 = ∓2 & y1 = -6,18
Eqns. Of normal are x+14y-254=0 & x+14y+86=0.
Question 23: Prove that the curves x = y2 and xy = k cut at right angles if
8k2 = 1. [Hint: Two curves intersect at right angle if the tangents to the
curves at the point of intersection are perpendicular to each other.]
Answer: 23 after solving two curves , we get y=k1/3 & x=k2/3 , find slopes
At this point
Question 25: Find the equation of the tangent to the curve
which is parallel to the line 4x − 2y + 5 = 0.
Answer 25: dy/dx= at (x1,y1) , slope of line is 2 by equating , we
get x1 =41/48 & y1 = ¾ , eqn. Is 48x-24y=23.
Ex. 6.4 Question 1:

1. Using differentials, find the approximate value of each of the following
up to 3 places of decimal

(i) (ii) (iii) (iv) (v) (vi)

(vii) (viii) (ix) (x) (xi)

(xii) (xiii) (xiv) (xv)

Answer(i) let x=25 , △x=0.3 (iii) let x= 0.64, △x= -0.04 , = 0.8 +△y

& △y = (dy/dx).△x= -(0.04)/2x0.8= -0.025∴ = .775

(iv) let x= 0.008, dx=0.001 , △y= (dy/dx) x [ △y/△x=dy/dx (app.)]
△y = .001= .001=1/120=.008

(x+△x)1/3 – x1/3 = (.009)1/3 – 0.2⇨ (.009)1/3 = 0.2+△y= 0.2+.008=.208(app.)
(v) let x= 1, △x= -0.001 , dy △y = -.0001 ,answer is (0.999)1/10=0 .9999
(viii) let x= 256 △x=-1 , △y = (x+△x)1/4 – x1/4 ⇨(255)1/4 = 4+△y ,

dy/dx=1/(4x3/4) ∴ △y= (dy/dx).△x= . (-1)= -1/256 =-0.0039,

so (255)1/4 = 4+△y = 3.9961.

(xii) let x= 27, △x= -0.43 ,△y= . (-0.43)= -0.015926 , ans. =2.984(app)

(xiv) let x= 4, △x= -0.032 , △y= (3√4/2)x-0.032=0.096 ,ans. =8-.096=7.904
Question 5: Find the approximate change in the surface area of a cube of
side x metres caused by decreasing the side by 1%
Answer 5: approximate change in the surface area=△s= ds/dx.△x=
12x. (-0.01x)= -0.12x2 m2
Question 7: If the radius of a sphere is measured as 9 m with an error of
0.03 m, then find the approximate error in calculating in surface area.
Answer 7: △s = ds/dr.△r= 8пr .(0.03)= 2.16п m2
EX. 6.5 Question 2: Find the maximum and minimum values, if any,

of the following functions given by

(i) f(x) = |x + 2| − 1 (ii) g(x) = − |x + 1| + 3 (iii) h(x) = sin(2x) + 5

(iv) f(x) = |sin 4x + 3| (v) h(x) = x + 1, x (−1, 1)

Answer: (i) |x + 2|≥0, x ∊R ∴ f(x)≥-1(mini.), no max. Value same as (ii)

Part (iii) -1≤sin2x≤1, so max. Valueof f(x) is 6 & mini. Value is 4 (iv) max.
Value of f(x) is |1+3|=4 & mini. Value is 2. (v) no max. Or mini. However,
greatest & least value as at x=1,-1 f(x)=2 & 0.

Question 3: Find the local maximum value and the local minimum value of
the functions(if any) in the given intervals: (iii) h(x) = sinx + cosx,

(0, п/2) (vi) g(x) = x/2+2/x, x>0 (Vi)f(x)=x , x>0

Answer: 3 (iii) h’(x)=cosx(1-tanx)=0⇨ tanx=1,x=п/4∊(0, п/2)
By 1st derivative test, at x= п/4, we will check nature of h’(x)
X<п/4 to x>п/4 , h’(x) changes it’s sign from +ve to –ve , local max.
Value at п/4 is f(п/4) = √2 or second derivative test , we will find
h’’(x)= -sinx – cosx, put x=п/4 ,we get h’’(x) <0⇨ max. At п/4.
(vi) g’(x)= ½ - 2/x2 =0⇨ x=∓2, x=-2 is rejected so we will check at x=2
Both tests can be applied g,(x) changes its sign from –ve to +ve as x
increases , g(x) has local minima at x=2 & local mini. Value is 2 0r second
derivative test ⇨ g’’(x) = 4x-3 >0 at x=2.
(vi) f’(x) =0 ⇨ x=2/3 , f’(x) changes sign from +ve to –ve as x
increases through x=2/3, local max. Value is 2√3/9.
Question 8: At what points in the interval [0, 2π+, does the function
sin 2x attain its maximum value?
Answer 8: f’(x)=2cos2x=0 ⇨ x= п/4, 3п/4 ,5п/4 ,7п/4 , so max. Value
Of f(x) is 1 at x= п/4 ,5п/4.
Question 11: It is given that at x = 1, the function x4− 62x2 + ax + 9 attains
its maximum value, on the interval [0, 2]. Find the value of a.
Answer 11: f’(x) =4x3-124x+a =0 ⇨ x=1 , f’(1) =0 ⇨ a=120, f’’(x)<0 at 1
F(x) has max. At x=1, when a=120
Question 12: Find the maximum and minimum values of x + sin 2x
on [0, 2π+.
Answer 12: f’(x) = 1+2cos2x=0 ⇨ cos2x= -1/2⇨ 2x= 2п/3, 4п/3 ,8п/3,
10п/3 ⇨ x= п/3, 2п/3 ,4п/3, 5п/3 , we get max. F(x)=2п & mini. =0
Question 17: A square piece of tin of side 18 cm is to made into a box
without top, by cutting a square from each corner and folding up the
flaps to form the box. What should be the side of the square to be
cut off so that the volume of the box is the maximum possible?
Answer 17: volume of box= x(18-2x)2 ( x is the side of square)
Dv/dx= (18-2x)(18-6x)=0⇨ x=3, 9,x≠9, d2v/dx2 = -72< 0 at x=3
*Question 18:A rectangular sheet of tin 45 cm by 24 cm is to be made

into a box without top, by cutting off square from each corner and
folding up the flaps. What should be the side of the square to be cut
off so that the volume of the box is the maximum possible?
Answer 18: v= 2x(45-2x)(12-x), dv/dx= 12(x2-23x+90) =0 ⇨ x= 5,18
d2v/dx2 < 0 at x=5 (x can’t be greater than 12)

Question 20 Show that the right circular cylinder of the given surface and
max. Volume is such that its height is equal to the diameter of the base.

Answer 20: S= 2пr2 +2пrh ⇨ h = , V =пr2( ) , dV/dr=0⇨

S=6пr2 ⇨ h=2r, find d2v/dr2<0

*Question 21: Of all the closed cylinder cans (right cylinder) of a gven

Volume of 100 cubic cm., find the dims. Of can which has the mini.
Surface area?

Answer 21: V= пr2h =100⇨ h= 100/ пr2 , S= 2пr2 +2пr(100/ пr2)

Ds/dr=0⇨ пr3 =50 ⇨ r= (50/п)1/3 , find its 2nd derivative >0

Question 22: A wire of length 28 m is to be cut into two pieces. One

of the pieces is to be made into a square and the other into a circle.

What should be the length of the two pieces so that the combined

area of the square and the circle is minimum?

Answer 22: let one part be x= 2пr & another 28-x be the per. Of square

∴ r=x/2п & side of square is (28-x)/4 ⇨ A = x2/4п + [(28-x)/4]2

dA/dx=0 ⇨ x=28п /(4+п) , find d2A/dx2 >0 ⇨ A is mini.

Question 23:Prove that the volume of the largest cone that can be

inscribed in a sphere of radius R is of the volume of the sphere.

Answer 23: Draw cone inside the circle R=OA=OP be radius & Ѳ=angle

AOC (PC is height of cone),Consider △AOC, find V= 1/3 п (AC)2(PC)

= 1/3 ПR3 sin2Ѳ(1+cosѲ) * ∵PC=PO+OC] , Dv/dѲ =0 ⇨ cosѲ=1/3 or -1

cosѲ=1/3 [∵cosѲ≠-1 ∵ Ѳ ≠п], sinѲ = 2√2/3, find 2nd derivative <0

which gives max. Volume ,put the values of sinѲ, cosѲ,

we get V= 8/27(4/3ПR3)= 8/27(volume of sphere)

Question 24: Show that the right circular cone of least curved surface
and given volume has an altitude equal to time the radius of the
base. [Answer 24: V= 1/3пr h....(i) ⇨ h=3V/ пr2 put it in S = пrl ⇨
2

S2 = п2r 2(r2+h2) ⇨ S2 = п2r 2(r2+(3V/ пr2)2)= P(let) , dP/dr =0 ⇨
r6 = 9V2/2п2 ......(ii) , 2nd der. >0 ∀ +ve r , from (i) & (ii)
(by equating the values of V2), we get h=√2r.]
Question 25: Show that the semi-vertical angle of the cone of the
maximum volume and of given slant height is .
Answer 25: Let l , r, h be slant height, radius, height & Ѳ be the semi-
vertical angle , V= 1/3 п(lsinѲ)2(lcosѲ), dv/dѲ=0 ⇨ tanѲ =√2, f
ind 2nd der. <0 ⇨ max. Volume at Ѳ= tan-1√2.
Question 26: Show that the semi-vertical angle of the cone of given
surface and max. Volume is sin-1(1/3).
Answer 26: S=пrl+пr2 ......(i) ⇨ l = (S-пr2)/пr put in volume
=1/3пr²
Take squaring let it P, then derivative =0⇨ S=4пr², 2nd der. <0, put the
Value of S in (i) ⇨ r/l= sinѲ=1/3

Question 28:For all real values of x, the minimum value of is

(A) 0 (B) 1 (C) 3 (D) [ ans. (D), dy/dx=0⇨x=1,-1 & mini. At 1]

Question 29:The maximum value of is

(A) (B) (C) 1 (D) 0 [ans. (C) dy/dx=0⇨x=1/2]

Misc. Question 1: Using differentials, find the approximate value of

each of the following. (a) (b)

Answer 1: (a) (17)1/4/3, let x=16 & △x= 1, △y=(dy/dx).△x=1/32

∴ (17)1/4 = 2.03125 & ans. is 2.03125/3=0.677(app.) (b) x=32, △x=1

(33)1/5 =2+(1/80)=161/80 ∴ (1/33)1/5 = 80/161=0.497(app.)

Question 2:Show that the function given by
has maximum at x = e.
Answer 2: f’(x)= (1-logx)/x2 =0 ⇨ x=e,show f’’(x)<0 at x=e
Question 3:The two equal sides of an isosceles triangle with fixed
base b are decreasing at the rate of 3 cm per second. How fast is the
area decreasing when the two equal sides are equal to the base?
Answer 3: let AB=AC=x & BC=b, L is mid point of BC.Consider △ABL
AL= , Area = ½ . b. , dA/dt= (dA/dx).(dx/dt) at x=b
Where dx/dt =3cm./sec (given). Ans. is √3 bcm2 /sec.
Question 6: Find the intervals in which the function f given by

is (i) increasing (ii) decreasing

Answer 6: f’(x)= , 4-cosx>0 ∵ -1≤cosx≤1 ∴ f’(x)>0or <0

Depend on cosx>0 or<0 ∴ f is ↑ when 0<x<п/2 , 3п/2<x<2п & ↓ when
п/2<x<3п/2
Question 7:Find the intervals in which the function f given by

is (i) increasing (ii) decreasing
Answer 7: f’(x) 3x – 3/x4 >0 ⇨ (x3-1)(x3+1)>0 ⇨ (x3-1)>0 &(x3+1)>0
2

Or (x3-1)<0 & (x3+1)<0⇨ f is ↑ when x<-1 & x>1, ↓ when -1<x<1
Question 8:Find the maximum area of an isosceles triangle inscribed

in the ellipse with its vertex at one end of the major axis.
Answer 8: let end vertex be A(a,0), P(acosѲ, bsinѲ)& Q be two on ellipse
PQ intersect x-axis of ellipse at R. Area of isosceles △APQ = ½.PQ.AM
=1/2 (2bsinѲ)(a-acosѲ) = ab(sinѲ-(1/2) sin2Ѳ) , dA/dѲ=0⇨ Ѳ=2п/3
Show 2nd der. <0 at Ѳ=2п/3, max. Area is (3√3/4)ab at Ѳ=2п/3
*Question 9:A tank with rectangular base and rectangular sides, open
at the top is to be constructed so that its depth is 2 m and volume is
8 m3. If building of tank costs Rs 70 per sq meters for the base and Rs
45 per square metre for sides. What is the cost of least expensive tank?
Answer 9: V= 2xy =8 ⇨ xy=4...(i) Area of base = xy, Area of sides =
2.2(x+y)=4(x+y), cost of construction = Rs. {70xy+180(x+y)}.....(ii)
From (i) & (ii) cost = 280+180(x+4/x), dC/dx =0 ⇨ x=∓2⇨ Cost is mini.
At x=2∴ y=2 , least cost is 1000.
*Question 10: The sum of per. Of a circle and a square is k, where k is
some constant. Prove that the sum of their area is least when the side
of square is double the radius of the circle.
Answer 10: 4x+2пr =k (x is a side of square, r is radius) ⇨ x = (k-2пr)/4
Put the value of x in A= x2+пr2 , dA/dr =0 ⇨ r = k/(8+2п), show 2nd der.
>0 at r, then put the value of r in x ⇨ x=2r
*Question 11:A window is in the form of rectangle surmounted by a
semicircular opening. The total perimeter of the window is 10 m. Find the
dimensions of the window to admit maximum light through the whole
opening.
Answer 11: let width, length be x, 2r so per. = 2x+2r+1/2 .2пr= 10...(i)
A = 2RX+1/2 Пr2 ...(ii) , from (i) & (ii) ⇨ A= 10r – (1/2п+2)r2 , dA/dr=0

⇨r = , find 2nd der.<0 at r , length=2r=20/(п+4), breadth=
*Question 12:A point on the hypotenuse of a triangle is at distance a
and b from the sides of the triangle.Show that the minimum length

of the hypotenuse is
Answer 12: Draw a right angled △, AB, BC, AC are per. , base & hyp. Resp.
Draw PL parallel to BC, PM is parallel to AB . angle C is Ѳ. Consider △
APL & PCM ⇨ l= AP+PC ⇨asecѲ+bcosecѲ, 0<Ѳ<п/2, dl/dѲ=0

⇨tanѲ=(b/a)1/3 , show 2nd der. >0, least value of l=
Question 13: Find the points at which the function f given by

Has (i) local maxima (ii) local minima (iii) point of inflexion

Answer 13: f’(x)=0⇨ x=2, -1, 2/7 f(x) is mini. At x=2, x=-1 is point of
inflexion( does not change its sign) & max. At x=2/7
Question 15: Show that the altitude of the right circular cone of

maximum volume that can be inscribed in a sphere of radius r is .
Answer 15: Take OB is radius, AM is height of cone, BC is base of cone
M is mid point of BC, angle BOM=Ѳ. AM= AO+OM=r(1+cosѲ)
V= 1/3 пr3sin2Ѳ(1+cosѲ, dV/dѲ= 0⇨ cosѲ=1/3,cosѲ ≠-1,show 2nd der.
<0, then find altitude = r(1+cosѲ)= 4r/3
Question 17: Show that the height of the cylinder of maximum volume

that can be inscribed in a sphere of radius R is . Also find the
maximum volume.
Answer17 : Radius of sphere is R, x & h diameter , height of cylinder
h2+x2=(2R)2 ....(i) , V= п.(x/2)2.h = ¼ пh(4R2-h2) from(i), dV/dh=0

⇨h = , show 2nd der. <0 at h & max. Volume is .
Question 18: Show that height of the cylinder of greatest volume

which can be inscribed in a right circular cone of height h and semi
vertical angle α is one-third that of the cone and the greatest volume

of cylinder is .
Answer 18: vertical angle be (cone) OO’ is height of cylinder = VO-VO’
= h-xcot ( O’ ,O are centre of top & bottom of cly.), V= Пx2( h-xcot )
Dv/dx=0 ⇨ x=(2п/3)tan , show 2nd der. <0 & max. Volume at x.
Question 20:The slope of the tangent to the curve

at the point (2, −1) is(A) (B) (C) (D)
Answer 20: (B) , put x=2 ⇨ t = - 5,2 then put t=2 ⇨ y=-1
dy/dx= 4t-2/2t+3 = 6/7 at t=2.

ASSIGMENT OF DIFFERENTIATION
Question 1Show that y = aex and y = be –x cut at right angles if
ab=1 [by equating , we get ex = ⇨ x= ½ log ( b/a) , find
slopes(dy/dx) at pt. of intersection is (½ log ( b/a , ).

Question 2 (i) If y +x = 1, prove that

dy/dx= (-1)

[Hint: put y=sinѲ & x= sin , use formula of sin(
(ii) If cos-1 ) = tan-1a , find dy/dx.
[let cos(tan-1a )= k(constant), then assume c= 1-k/1+k , dy/dx= y/x]
(iii) If = , prove that dy/dx =
(iv) If xm.yn = (x+y)m+n, then find dy/dx. [ y/x]
Question 3 Differentiate w.r.t. x :
**(i) Using logarithmic differentiation, differentiate:

Solution:

x logx
(ii) + (iii) (iogx) + x
Question 4 (i) If = , prove that dy/dx =
(ii) If f(1)= 4,f’(1)=2,find d/dx{logf(ex)} at the point x =0.[1/2]

(iii)If y = ,show that (2y – 1)dy/dx =1.
a (t+1/t)
(iv) If x = (t+1/t) , y= a where a>0,a≠1,t≠0, find dy/dx.
[Hint: take dy/dt & dx/dt , then find dy/dx = ylogy/ax. ]
Question5
(i)differentiate: Sec-1(1/(2x2 – 1)),w.r.t.sin-1(3x –4x3).
[Hint: let u=1st fn. & v= 2nd fn. , find du/dv = 1]
(ii)differentiate: tan-1 ( ),w.r.t. sin-1 ( ) if 1<x<1;x≠0
[ du/dv= ¼, put x=tanѲ⇨ u=Ѳ/2, v=2Ѳ , u&v as assumed above]
(msin-1x)
(iii) If y = e , show that (1-x2)y2 – xy1 – m2y= 0.
Question 6 Water is driping out from a conical funnel, at the
uniform rate of 2cm3/sec. through a tiny hole at the vertex at
the bottom. When the slant height of the water is 4cm.,find
the rate of decrease of the slant height of the water given that
the vertical angle of the funnel is 1200 .
[Let l is slant height ,V = 1/3. .l /2.l/2= l3/8(vertical angle
will be 600 (half cone), take dv/dt=-2cm3/sec. ⇨l=-1/3 cm/s.]
[Hint: put y=sinѲ & x= sin , use formula of sin(

(ii) If cos-1 ) = tan-1a , find dy/dx.
[let cos(tan-1a )= k(constant), then assume c= 1-k/1+k , dy/dx= y/x]
(iii) If = , prove that dy/dx =
(iv) If xm.yn = (x+y)m+n, then find dy/dx. [ y/x]
Question 3 Differentiate w.r.t. x :
**(i) Using logarithmic differentiation, differentiate:

Solution:

x logx
(ii) + (iii) (iogx) + x
Question 4 (i) If = , prove that dy/dx =
(ii) If f(1)= 4,f’(1)=2,find d/dx{logf(ex)} at the point x =0.[1/2]

(iii)If y = ,show that (2y – 1)dy/dx =1.
a (t+1/t)
(iv) If x = (t+1/t) , y= a where a>0,a≠1,t≠0, find dy/dx.
[Hint: take dy/dt & dx/dt , then find dy/dx = ylogy/ax. ]
Question5
(i)differentiate: Sec-1(1/(2x2 – 1)),w.r.t.sin-1(3x –4x3).
[Hint: let u=1st fn. & v= 2nd fn. , find du/dv = 1]
(ii)differentiate: tan-1 ( ),w.r.t. sin-1 ( ) if 1<x<1;x≠0
[ du/dv= ¼, put x=tanѲ⇨ u=Ѳ/2, v=2Ѳ , u&v as assumed above]
(msin-1x)
(iii) If y = e , show that (1-x2)y2 – xy1 – m2y= 0.
Question 6 Water is driping out from a conical funnel, at the uniform

rate of 2cm3/sec. through a tiny hole at the vertex at the bottom.
When the slant height of the water is 4cm.,find the rate of decrease
of the slant height of the water given that the vertical angle of the
funnel is 1200 .
[Hint: Let l is slant height ,V = 1/3. .l /2.l/2= l3/8(vertical angle
will be 600 (half cone), take dv/dt=-2cm3/sec. ⇨l=-1/3 cm/s.]
**Question 7(i) Let f be differentiable for all x. If f(1)=-2 and f f f `(x) ≥2
∀ x∊[1, 6], then prove f(6) ≥8.[ use L.M.V.Thm.,f`(c)≥2,c∊[1, 6]]
(ii) If the function f(x)= x3 – 6x2+ax+b defined on [1, 3] satisfies the
rolle’s theorem for c = (2 +i)/ , then p.t. a = 11 & b∊R.
[Hint: Take f(1)=f(3) , use rolle’s thm. f`(c)=0⇨ a=11]
Question 8 (i) Show that f(x)= x/sinx is increasing in (0, п/2)
*HINT: f’(x)>0 , tanx >x+
(ii) Find the intervals of increase and decrease for f(x) = x3 + 2x2 – 1.
[Answer is increasing in (-∞, -4/3)U(0, ∞) & decreasing in (-4/3, 0)]
(iii) Find the interval of increase&decrease for f(x) =log(1+x)-(x/1+x)
OR
Prove that x/(1+x) < log(1+x) < x for x > 0.
[ Hint: f(x)strictly ↑ in [0, ∞) , x>0 ⇨f(x)>f(0), let g(x)=x-log(1+x)
g(x)>0 ↑ in [0,∞) & f(x) ↓ in (-∞, 0].]
(iv) For which value of a , f(x)=a(x+sinx)+a is increasing.
[Hint: f’(x) a(1+cosx) ≥0 ⇨ a>0 ∵ -1≤cosx≤1]
**Question 9 Problem: Using differentials, approximate the expression
[ arctan(1.05) = tan-1(1.05)]

Solution:

We let

Hence,

x = 0.05 and y = /4.



Question 10 Find the stationary points of the function f(x) =
3x4 – 8x3+6x2 and distinguish b/w them. Also find the local max.
And local mini. Values, if they exist.
* f’(x)=0⇨ x=0,1 f has local mini. At x=0∵f’’>0 & f’’’’(1)≠0, f has point of
inflexion at x=1,f(1)=1]
Question 11 Show that the semi – vertical angle of right circular cone of
given total surface area and max. Volume is sin-1 1/3.
[Hint: take S=Пr(l+r) ⇨ l= S/пr – r , take derivative of V² OR can use
trigonometric functions for l & h]
Question 12 A window has the shape of a rectangle surmounted by an
equilateral ∆. If the perimeter of the window is 12 m., find the dimensions
of the rectangle so that it may produce the largest area of the window.
[Hint: let x=length, y=breadth, then y=6 – 3y/2, A= XY+ X2 /4, take
derivative of A & it is max. ,x=4(6+ )/11 ,y=6(5 )/11]

Application of derivatives

Recommended

Recommended

More Related Content

What's hot

What's hot (20)

Similar to Application of derivatives

Similar to Application of derivatives (20)

More from indu thakur

More from indu thakur (11)

Recently uploaded

Recently uploaded (20)

Application of derivatives