The document defines matrices and their properties, including symmetric, skew-symmetric, and determinant. It provides examples of solving systems of equations using matrices and their inverses. It also discusses properties of determinants, including properties related to symmetric and skew-symmetric matrices. Inverse trigonometric functions are defined, including their domains, ranges, and relationships between inverse functions using addition and subtraction formulas. Sample problems are provided to solve systems of equations and evaluate determinants.

1. MATRIX:
Definition: A matrix is defined as an ordered rectangular
array of numbers.
Elementary Transformation
3. Ri → Ri + kRj means multiply each element of jth
row by k and add it to the corresponding elements of ith
row.
4. In applying one or more row operations while
finding A-1 by elementary row operations, we
obtain all zeros in one or more, then A-1 does not
exist.
NOTE If A is symm. As well as skew-symm., then A is
a null matrix.( if A = AT then A is Symm. And if A = - AT
then A is skew- symm.)
A= is symmetric and B is
skew-symmetric.
NOTE: (i) If A and B are symmetric matrices, then
BA-2AB is neither symm. nor skew-symm.

2. (ii) If A is symm. matrix then BTAB is symm. (iii) If A
and B are symmetric matrices of same order, then AB is
symm. iff AB=BA (iv) Zero matrix is both symm. and skew-
symm. (v) Sum of two skew-symm. matrices is always skew-
symm (vi) If A is a symm., then A3 is a symm. and if A is
skew-symm., then A2 is a symm.
The Determinant of a Matrix
DEFINITION: Determinants play an important role in
finding the inverse of a matrix and also in solving systems of
linear equations. In the following we assume we have a square
matrix (m = n). The determinant of a matrix A will be
denoted by det(A) or |A|. Firstly the determinant of a 2×2 and
3×3 matrix will be introduced, then the n×n case will be
shown.
Consistent and Inconsistent
Solutions
Consistent system : A system of equation is said to be
consistent if its solution ( one or more ) exists.
Inconsistent system : A system of equation is said to be
inconsistent if its solution does not exist.
Working rule to check consistency:
Case I When A0 System is consistence and has unique
solution. Case II When A=0 .Find Adj(A) and then find Adj(A)
.B. If Adj(A) .B 0 then system is inconsistence .
Case III If Adj(A).B=0 Then it may have infinite solutions then it
is consistence or have no solution then it is inconsistence.
Properties of Determinants:
Property 1. If each element of a row (column)ofdeterminant is
zero , then value of determinant is zero.
Property 2. Value of a determinant is not changed by
changing the rows into columns and columns into rows.

3. Property 3. If two adjacent rows (columns)of a determinant are
interchanged , then the sign of the determinant is changed but
its numerical value is unchanged.
Property 4. If two rows (columns) are identical, then the value
of the determinant is zero.
Property 5. If every element of a row (column) is multiplied by
some constant k,the value of the determinant is multiplied by
k.
Property 6 .If each element in any row (column) consist of two
terms , then the determinant can be expressed as the sum of
the determinants of same order.
Property 7 . The value of a determinant remain unchanged if to
each element of a row (column) be add ( or subtracted)
equimultiplies of the corresponding elements of one or more
rows (columns) of the determinant.
Property 8. The value of the determinant of a diagonal matrix
is equal to the product of the diagonal elements.
Property 9. The value of the determinant of a skew-symmetric
matrix of odd order is always zero.
Property 10. The determinant of a symmetric matrix of even
order is always a perfect square.
ASSIGNMENT(matrices)
Qoestion.1 Using matrices, solve the following system of equations
(i) x+2y+z = 1 , 2x – y+z = 5 , 3x+y – z = 0.
[Hint use AX = B ⇨ X = A-1 B, |A|=15≠0 means A is invertible. Adj(A) =
,A-1 = Ans. x =1, y=-1, z=2]
(ii) 2x+y – 3z = 13, x + y – z = 6 , 2x – y+4z = -12.
[ Ans. |A| = 9, adj(A) = , x=1, y=2, z=-3.]

4. (iii) 2x+y+z = 1 , x – 2y – z = 3/2 , 3y – 5z = 9.
[Hint |A| = 34, adj (A) = , x=1, y= 1/2., z=-3/2.]
Question.2 Use the product to solve
the equations x – y+z = 4, x – 2y – 2z = 9, 2x+y+3z = 1.
[Hint take product of above two matrices, we get identity matrix,
then use AB=BA = I means B is the inverse of A
Or A is the inverse of B.
⇨ = 8I3 ,
according to above equation let A
let B (1/8) B is the inverse of A. Ans. x=3, y=-2, z=-1.]
Question.3 Solve the following system of homogenous equations:
2x+3y – z = 0, x – y – 2z = 0, 3x+y+3z = 0.
Solution: system of homogenous equations can be written as AX = O
,A= ,|A| = -33
So, the system has only the trivial solution given by x=y=z=0. If |A| =
0 then system has non-trivial solution.]
Question.4 Show that system of equations x+y – z = 0, x – 2y+z = 0,
3x+6y – 5z = 0 has non-trivial solution. Find sol.Answer: |A| = 0, it
has infinitely many solutions ∴ let z = k a arbitrary x+y = z = k , x –
2y = -z = -k , 3y = 2k i.e, y = 2k/3 ⇨ x = k/3 from first equation by
putting the values of x, y & z in third equation, we get 0 which is true.
The required solution is z = k, y = 2k/3, x = k/3 where k is arbitrary.

5. Question.5 Show that system of equations3x+2y +7 z = 0, 4x – 3y - 2z
= 0, 5x+9y +23z = 0 has non-trivial solution. Find the solution. [Hint
x = -k, y = -2k, z = k]
Question.6 The system of equations 2x+3y = 7 , 14x+21y = 49 has
(a) only one solution (b) finitely many solution (c) no solution (d)
infinitely many solution . [give reason]
Question.6 Find the inverse (using elementary transformations) of
following matrices: (i) A =
[Hint: A-1 = ,R1↔R2,R3→R3 –
3R1,R3→R3+5R2,R1→R1 – 2R2,R2→R2 – R3, R1→R1+(1/2)
R3,R3→(1/2)R3]
(ii) A = [Hint: A-1 =
,R1↔R3,R3→R3 – 3R1,R1→R1+R2,R2→1/2R2,R3→R3 – 10R2,
R3→-R3,R1→R1 – 3R3,R2→R2+3/2R3]
(iii) A = [Hint: A-1 =
,R2→R2+R1+R3,R3→R3 –
2R1,R1→R1+3R3,R3→8R3,R3→R3+R2
R3→1/25R3,R1→R1 – 10R3,R2→R2+7R3,R2→1/8R2]
Question. If A is singular matrix then underwhatcondition set of
equations AX = B may beconsistent. [answer if (adjA)B = O ,then
eqns. Will have infinitly many sols. Hence consistent.]

6. Question. If A is a square matrix of order 3 such that |adjA| = 289,
find |A|. [ |A| = ±17 ∵ |adjA| = |A|n-1.]
ASSIGNMENT ( WITH HINTS)(determinant)
Question: (i) Let = and = , then
- =0
[Hint = ]
(ii) If f(x) = , then which is correctf(a)=0 ,
f(b)=0, f(0)=0 and f(1)=0 [ Hint f(0)=0 det.(skewsymm.matrix)=0].
**(iii) Let f(t) = , then is equal to 0,1,2,3.
[Hint 0, = → as t→ ].
(iv) There are two values of a which makes determinant =
= 86, then sum of these numbers is 4,5,-4,9. [Hint
a=-4, operate R2 – 2R1]
Question.1 Prove that the points P (a, b+c), Q(b, c+a), R(c,
a+b) are collinear.
Answer : If P,Q and R are collinear then =0

7. By applying C2 → C2+C1 = (a+b+c)
=0 ( ∵ C2, C3 are identical)
Question.2 Find the value of k if the area of the triangle with
vertices (-2,0),(0,4) and (0,k) is 4 square units.
Answer: Area of =½ =4
⇨ the absolute value of ½ (-2)(4 – k) = 4 ⇨ the absolute
value of (k – 4) = 4 ⇨ |k – 4| = 4 ⇨ k – 4 = 4, -4 ⇨ k = 8, 0.
Question.3 Without expanding, show that
(i) =0
Operating C1 → C1+C2+C3, we get = 0.
(ii) = 0 Taking out (-1) from C1,C2 and C3, we
get, = (-1)(-1)(-1) = -1 =
- (by interchanging rows and columns) 2 =0 ⇨ =0
(iii) =0 ⇨
=
= abc

8. ( Operating C3 → C3+C1)
abc(ab+bc+ac) x 0 = 0 ( two cols. Are identical)
(iv) =0 ⇨ - =
-
- = 0 (PassC3overthefirsttwocolumns.)
(v) =
R.H.S. = ( applying C1 ↔
C2)
= - (apply C3 → C3 – (ab+bc+ca))C1)
= =
(apply C2 ↔ C3 and C1 ↔ C2)
Q. If a,b,c are +ve and are the pth,qth and rth terms resp. Of a
G.P.,show without expanding that

9. ** (vi) =0 (put a=xyp-1 ,b=xyq-1 ,c=xyr-1 ,
apply C1 →C1-logx.C3 ,C1→C1+C3)
(vii) = (same method as given below)
(viii) =
( Multiply by abc as R1 with a,R2 by b and R3 by c then divide with
abc )
Find the values of: (ix) (Operate C2 → C 2.
and value is 0
(x)
(Operating C3 → C3 – cos .C2+ sin .C1 and value is 0)
Q. Prove that :
(a)
= (1+a2+b2)3 ( Apply C1 → (C1 - bC3) and C2 → (C2+aC3)
(b) = 1 (Apply R3 → sin R3 +
cos R1)

10. (C) = xyz(x+y+z)3 (Apply R1
→ x R1, R2 → y R2, R3 → z R3 and take x,y,z common from
C1,C2,C3 resp.)
(d =(a-b)(b-c)(c-a)(a+b+c)(a2+b2+c2 )
( Apply C1 → (C1+C2 – 2C3)
(e) = 2(a+b)(b+c)(c+a)
(Apply C1 →(C1+C3 )and C2 →(C2+C3))
(f) = (a+b+c)(a2+b2+c2)
(g) = 2 (apply C1→C1-C2-C3,
C2→C2-C1,C3→C3-C1, C2↔C3)
(h) = abc ( + + +1(ab+bc+ca+abc).
(Hint taking a,b,c common from each row , apply
R1→R1+R2+R3 then expand along first row).
(i) = )3
Apply C1→C1-b C3, C2→C2+a C3, we get

11. =( expand along C1, We
get ( .
**(h) Evaluate where =C(x,1) ( binomial
coefficient)
Solution: =
( taking x,y,z common from
R1,R2,R3 resp. and ½!,1/3!
From C2,C3 resp.) ( by formula of C(n,r) = )
Apply C3→C3 + C2 and put a= x-1, b=y-1, c=z-1
= (a-b)(b-c)(c-a) = (x-y)(y-z)(z-x).
Question: If x,y,z are all different and if =0
, prove that xyz = -1
Solution: = + =
+ xyz =0

12. (1+xyz) = 0 ⇨ (x-y)(y-z)(z-x)(1+xyz) = 0 ⇨
xyz=-1 ∵ x ≠y≠ z.
Question: By using properties of determinant,show that
= 1+a2+b2+c2
[Hint: multiply and divide by a,b,c with R1,R2,R3
respectively,taking a,b,c common from C1,C2,C3 respectively
R1→R1+R2+R3]
Question: show that
=(a+b+c)3.[Hint:R1→R1+R2+R3+
Question(i) Using matrix method, solve the following system of
equations:
+ + = 4, - + = 1, + - = 2; x, y, z ≠ 0.
[X=2,Y=3,Z=5,|A|=1200,adjA = ]
(ii) - + =4, + - = 0, + + =2
[ x=1/2,y=-1,z=1 adjA= |A| = 10]
(iii) - + = 10, + + = 10, - + =13; X, Y, Z ≠ 0.

13. [X=1/2,Y=1/3,Z=1/5,|A|=-9, adjA = ]
Inverse Trigonometric Functions
Table of domain and range of inverse trigonometric function
Inverse-forward identities are

14. Forward-inverse identities are
Relation between inverse functions:

16. For suitable values of x and y
sin-1 x + sin-1 y= sin-1 (x√1-y2+ y√1-x2)
sin-1 x - sin-1 y=sin-1 (x√1-y2- y√1-x2)
cos-1 x + cos-1 y= cos-1 (xy- √1-x2√1-y2)

17. cos-1 x - cos-1 y= cos-1 (xy+√1-x2√1-y2)
tan-1 x + tan-1y = ; xy<1
tan-1 x – tan-1 y= ; xy>-1
2tan-1 x= = =
Trigonometry examples
Example 1:
Solve the following equation:
Suggested answer:

18. Problems – Solve Inverse Trigonometric Functions
Problems:
Problem 1:

19. Prove that + = , x<
Solution:
Let x = tan θ , then θ = tan-1 x. we have
You will take R.H.S to prove the given expression
R.H.S =
= tan-1 (tan 3θ)
= 3 θ = 3 tan-1 x
= tan-1 x + 2 tan-1 x
= + = L.H.S
Hence, the given expression will be proved.
OR
Wecantake L.H.S. = + =
By using
tan-1 x + tan-1y = =R.H.S.
Example problem 2:
Solve tan-1 2x + tan-1 3x = π/4
Solution:
Given: tan-1 2x + tan-1 3x = π/4
Or

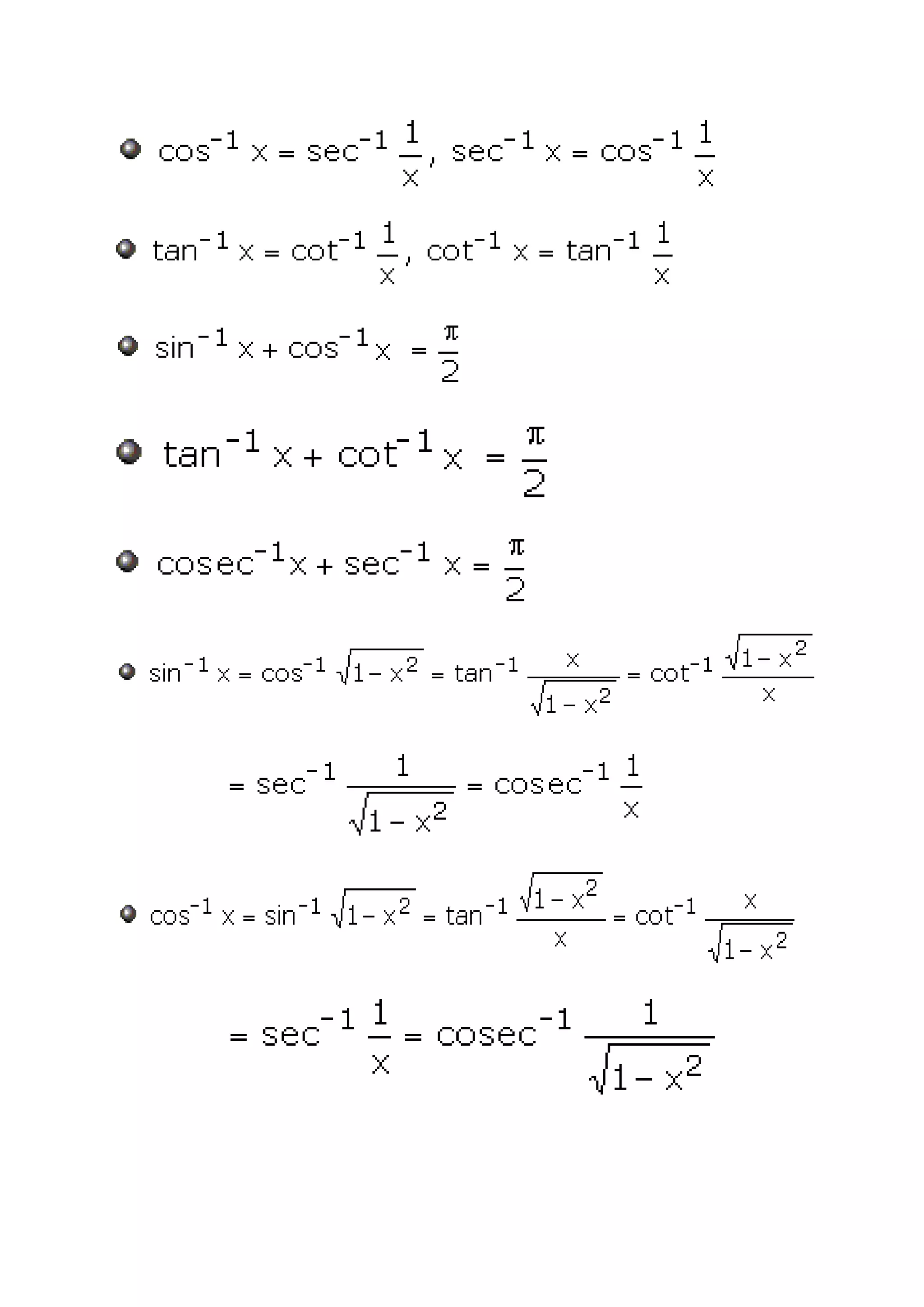
20. tan-1 ((2x + 3x)/(1 - 2x . 3x)) = π/4
tan-1 ((5x)/(1 - 6x2)) = π/4
∴ (5x)/(1 - 6x2) = tan π/4 = 1
or
6x2 + 5x – 1 = 0
That means, (6x – 1)(x + 1) = 0
Which gives
x = 1/6 or x = -1
since x = -1 does not satisfy the equation ,the equation of
the L.H.S is negative, so x = 1/6 is the only solution of the
given equation.
ASSIGNMENT:
Question.1 Evaluate: (i) sin-1(sin10) (ii) cos-1 (cos10)
(iii) tan-1(tan(-6))
Answer: (i) if –π/2 ≤x ≤π/2, then sin-1(sinx)=x but x= 10
radians does not lie between –π/2 and π/2
3π – 10 lies between –π/2 and π/2 ∴ sin-1(sin(3π-
10)) = 3π-10.
Similarly for (ii) cos-1 (cos10) = cos-1 (cos(4π-10)) = 4π-
10. [10 radians does not lie between 0 and π. ∴ 0≤4π-10≤π]
For (iii) tan-1(tan(-6)) = tan-1(tan(2π-6)) = 2π-6 . { -6
radians does not lie in [ –π/2 , π/2]}
Question.2 If x = cos-1(cos4) and y = sin-1(sin3), then
which holds? (give reason)
(i) x=y=1 (ii) x+y+1=0 (iii) x+2y=2 (iv) tan(x+y) = -tan7.

21. Question.3 if + = , then prove that -
cos + = sin2
[Hint: + = - ]= ⇨
cos )2 = )2
Simplify it]
Question.4 *(i) sin-1x + sin-1y + sin-1z = π, then prove that
X4+y4+z4+4x2y2z2 = 2(x2y2+y2z2+z2x2)
(ii) If + + = π/2 ; prove that
xy+yz+xz = 1.
(iii) If + + = π , prove that x+y+z =
xyz.
[Hint: for (i) sin-1x + sin-1y = π - sin-1z ⇨ cos(sin-1x + sin-
1
y) =cos( π - sin-1z)
Use cos(A-B) = cosAcosB – sinAsinB and cos(π – )=
-cos
It becomes - xy = - and simply it.
[Hint: for (ii) tan-1 x + tan-1y = ]
Question.5 Write the following functions in the simplest
form:
(i) ) (ii) ) (iii) ,-
a<x<a

22. [Hint: for (i) write cosx = cos2x/2 – sin2x/2 and 1+sinx
=(cosx/2 +sinx/2)2 , then use tan(A-B), answer is π/4 – x/2 ]
[ Hint: for (ii) write cosx = sin(π/2 – x) and sinx = cos(π/2
– x), then use formula of 1-cos(π/2 – x)= 2sin2(π/4 – x/2) and
sin(π/2 – x) = 2 sin(π/4 – x/2) cos(π/4 – x/2)
Same method can be applied for (i) part also. Answer is
π/4 + x/2]
[ for (iii) put x=a cos , then answer will be ½ ]
Question.6 If y = )- , prove that
siny = tan2(x/2). [Hint: y = - 2 , use formula
2 = )]
Question.7 (i) Prove that + + = π.
(ii) Prove that )+ )+ ) = 0.
[Hint: for (i) = - = , then use
formula of tan-1 x + tan-1y = ]
(ii) [Hint: write = ]
Question.8 Solve the following equations:
(i) + = .
(ii) + = .
(i) [Hint: write = - , put = y]
(ii) [Hint: use ]

23. Question.9 Using principal values, evaluate )
+ ). [answer is π]
Question.10 Show that tan( ) = and justify
why the other value is ignored?
[ Hint: put =∅ ⇨ ¾ = sin2∅ = 2tan∅/(1+tan2∅),
find tan∅-
** SOME HOT QUESTIONS:
1. Which is greater tan 1 or tan-11?
2. Find the value of sin(2 ) + cos(
3. Find the value of x which satisfies the equation
+ = .
4. Solve the equation: + ) = -π/2.
5. Show that tan ) = ).
6. If = - ), then find the
general value of .
ANSWERS WITH HINTS:
1. Since 1> π/4 ⇨ tan1> 1> tan-11.

24. 2. sin(2 ) + cos( = sin2x + cosy ⇨ +
= + = .
3. + = sin( ) by using
sin(A+B)=sinA cosB + cosA sinB
⇨ x + (1-x) = ∵
sin( )=
⇨ 2x – x2 = 1 ⇨ x = 0 or ½.
4. = - - ) ⇨ 6x = sin[- -
)]
= -cos[ ] =
-cos[ ]=- etc.
5. 1/2(2 tan )) , use formula 2 =
and tan2x/2 = .
6. Put tan = t and use sin2 = and cos2 =
then put t/3 = T,answer is = nπ, nπ+π/4.
- = ½ ⇨ = ½
=½
= ½ (2T), then tan = 0 ,1.
ASSESSMENT OF Relations & functions for
class—XII Level—1

25. Q.1 Let f(x) = Find f(-1) ,f(4) and f(5).
Q.2 If f(x) = x2 - , then find the value of f(x) + f ( .
Q.3 Let Q be the set all rational numbers and relation on Q defined by
R = {(X, Y): 1+XY > 0}. Prove then R is reflexive and symmetric but not
transitive.
Q.4 Write the identity element for the binary operation *defined on
set R by a*b = 3ab/8 ∀ a, b ЄR.
Q.5 Show that the function f: R → R defined by f(x) = sin x is neither 1-1
nor onto.
Answers (Level—1)
Ans.1 f (-1) = 2, f (4) = 14, f(5)= 30. Ans.2 0. Ans.3 Consider any x, y Є Q,
since 1+x.x =1+x2 ≥ 1
⇨ (x,x)Є R ⇨ reflexive
Let (x,y) Є R ⇨ 1+xy > 0 ⇨ 1+yx > 0 ⇨ (y,x) ЄR ⇨ symmetric.
But not transitive . Since (-1, 0) and (0, 2) ЄR, because 1 > 0 by putting
values. But (-1, 2) ∉ R because -1<0. Ans.4 Let e be the identity
element in R. Then a *e =a =e*a ∀ aЄR ⇨ a*e =a ∀ a ЄR ⇨ e = 8/3 in
R. Ans.5 f is not 1-1 because sin 0 = 0 =sin π,so the different elements
o, π have same images. f is not onto because -1 ≤ sin x ≤ 1 for all x ЄR ∴
the range of f =[-1,1], which is a proper subset of R.
Level
Q.1 If f: R→ R is given by f(x) = (3 – x3)1/3 show that fof =Ig where Ig is the
identity map on R.

26. Q.2 Show that the function f: [-1, 1+ →R defined by f(x) = is 1-1 .
Find the range of f. Also find the inverse of the function f: [-1, 1+ →
range of f.
Q.3 Show that the function f: R → R defined by f(x) = cos (5x+2) is
neither 1-1 nor onto?
Q.4 If f: R → R be given by f(x) = sin2x +sin2(x+π/3) +cosx .cos(x+π/3) ∀
x Є R, and g: R → R be a function such that g(5/4) =1 , then prove that
(gof) : R → R is a constant function.
Q.5 Let R1=R – {-1} and an operation * is defined on R1 by a*b = a + b +
ab ∀ a, b Є R1 .
Find the identity element and inverse of an element.
ANSWERS OF Level—2
Ans.1 As f: R → R, fof exists and fof : R → R is given by (fof) (x) = f(f(x)) =
f(3 – x3)1/3 = (3 – ((3 – x3)1/3 )3 )1/3 = (3 – (3 – x3))1/3 =x ∀ x ЄR Ans.2 f is
1-1, as consider any x1, x2 Є *-1, 1] such that f(x1) = f(x2) ⇨ = ⇨
x1x2+2x1 = x1x2 +2x2 ⇨ x1 = x2 For the range of f
Let y = f(x) ⇨ y = ⇨ xy +2y =x ⇨ (y – 1) x= -2y ⇨ x =
As x Є *-1, 1], so -1 ≤ ≤1 , but (y – 1)2 >0 , y ≠ 1⇨ -(y – 1)2 ≤ (y-
1)2≤ (y – 1)2 ⇨ -(y2 – 2y +1) ≤ -2y2+2y ≤ y2 – 2y +1 ,y≠ 1
⇨ Y2 – 1 ≤ 0 and 0 ≤ 3y2 – 4y +1 ⇨ y ε *-1,1] and (y – 1/3) (y – 1) ≥ 0 ,y
≠ 1 ⇨y Є *-1,1+ and y ε (-∞ ,1/3+ U *1,∞) , y ≠ 1
⇨ y Є *-1,1+ and y ε (-∞ ,1/3+ U (1,∞)⇨ y Є*-1,1/3].
∴ its inverse exists as f is 1-1 and onto, to find f-1
= y ⇨ xy +2y =x ⇨ 2y = x (1 – y) ⇨ x= f-1(y) = x = .
Ans. 3 For f is not 1-1, 5x+2 = π/2 ⇨ x = (π – 4)/10

27. ∴ 5x+2 =π/2, again 5x+2 = 3π/2 ⇨ x = (3π – 4)/10, Now f ((π –
4)/10)) = cos*5((π – 4)/10) +2+ = cosπ/2 =0
f ((3π – 4)/10) = cos*5((3π – 4)/10) +2+ = cos3π/2 = 0.
For f is not onto, as -1 ≤ cos (5x+2) ≤1, then -1≤ y ≤1, range of f = *-1, 1]
= {y : -1≤ y ≤1 - ≠ co-domain R.
Ans. 4 ½[ 2sin2x +2sin2(x+π/3) +2cosx cos(x+π/3)+
f (x)= ½[ 1 – cos2x +1 – cos (2x+2π/3)+ cos (2x+π/3)+cosπ/3+
( As we know that 2sin2x= 1 – cos2x and 2cosA cosB= Cos(A+B) + cos(A-
B).)
½[5/2 – ,cos2x + cos(2x+2π/3)- + cos(2x+π/3) ⇨ ½[5/2 – 2cos(2x+π/3)
cos π/3 + cos(2x+π/3)+ = 5/4 ∀ x ЄR
∴ for any x Є R , we have (gof)(x) = g(f(x)) = g(5/4)=1 ,so it is constant
function.
Ans. 5 * can be shown to be a binary operation on R1 as let a ≠ -1, b ≠ -
1 . a*b = a+b+ab Є R – {-1} ⇨ a+b+ab ≠ -1
⇨ a(1+b)+(b+1) ≠0 ⇨ (a+1) (1+b) ≠0 ⇨ a ≠ -1 and b ≠ -1 which is
true.Now if e is the identity element, then a*e =a ⇨ a+e+ae =a ⇨ e
(1+a) = 0 ⇨ e =0 or a = -1 ⇨e =0 , 0 is the identity w.r.t. *
Let a’ be inverse of a, then a*a’ =0 ⇨ a+a’+aa’ = 0 ⇨ a’(1+a) = - a
∴ a’ = - a/(1+a) , is the inverse of a w.r.t. *.
ASSIGNMENT(continuity & differentiability) (XII)
**Question 1 Determine a and b so that the function f given by
f(x) = , x<п/2

28. =a, x=п/2
= , x>п/2 Is continuous at x=п/2.
Answer [a = 1/3 , b = 8/3] **Question 2 Find k such that following
functions are continuous at indicated point
(i) f(x) = at x=0
(ii) f(x) = (2x+2 - 16)/(4x – 16) , x≠2
= k, x = 0 at x=2. Answer [ (i) k=1,(ii) k=1/2]
**Question 3 The function f is defined as
If f(x) is continuous on [0,8], find the values of a and b. Answer
[a=3,b=-2]
** Question 4 If f(x) = is continuous in
the [-1,1], find p. Answer [p=-1]
**Question 5 Find the value of a and b such that the f(x) defined as
f(x) = is continuous for all
values of x in [0,п]. ANSWER [a=п/6 , b=-п/12]
** Question 6 Prove that = -4
[ Hint: Nr. Can be written as tanx(tanx-1)(tanx+1) =- [tanx(cosx-
sinx)(tanx+1)]/cosx

29. Cosx-sinx = cos )]
**Question 7 Prove that (i) = [ Hint:
put x= sinѲ]
(ii) ) = -3/2. [Hint: = & use
formula of ]
Question 8 f(x) = , =1 & =1, then p.t.
f(-2)=f(2)=1. [ Hint: =0]
Question 9 [Dr. = 2|sinx/2| & =1
|sinx/2| =+ve & -ve as x→0+ & x→0- , ⇨ limit does not exist]
Question 10 Show that the function
f(x) is continuous at x=0.
[Hint: use =1 , =1]
Question11 Show that f(x) = |x-3|,x∊R is cts. But not diff. at x=3.
[Hint:show L.H.lt=R.H.lt by |x-3| = x-3, if x ≥3 and –x+3, if x<3, L.hd=-1≠1(R.h.d)
Question 12 Discuss the continuity of the fn. f(x) = |x+1|+|x+2|, at x =
-1 & -2 [Hint:f(x) =
yes cts. At x=-1,-2
Question 13 Find the values of p and q so that f(x)
= is diff. at x = 1. [ answer is p=3 , q=5]

30. Question 14 For what choice of a, b, c if any , does the function
F(x)= becomes diff at x=1,2 & show that a=b=c=0.
Question15For what values a,b f(x)= is diff.at x=0
[Hint: L.H.d= 2 =1& R.H.d=a, since f‘(x)=0exists, a=2,b∊R]
ASSIGMENT OF DIFFERENTITION
Question 1 Show that y = aex and y = be –x cut at right angles
aab=1 [ by equating , we get ex = ⇨ x= ½ log ( b/a) , find
slopes(dy/dx) at pt. of intersection is (½ log ( b/a , ).
Question 2 (i) If y +x = 1, prove that
dy/dx= (-1)
[Hint: put y=sinѲ & x= sin , use formula of sin(
(ii) If cos-1 ) = tan-1a , find dy/dx.
[let cos(tan-1a )= k(constant), then assume c= 1-k/1+k , dy/dx= y/x]
(iii) If = , prove that dy/dx =
(iv) If xm.yn = (x+y)m+n, then find dy/dx. [ y/x]
Question 3 Differentiate w.r.t. x :
**(i) Using logarithmic differentiation, differentiate:
Solution:

31. x logx
(ii) + (iii) (iogx) + x
Question 4 (i) If = , prove that dy/dx =
(ii) If f(1)= 4,f’(1)=2,find d/dx{logf(ex)} at the point x =0.[1/2]
(iii)If y = ,show that (2y – 1)dy/dx =1.
a (t+1/t)
(iv) If x = (t+1/t) , y= a where a>0,a≠1,t≠0, find dy/dx.
[Hint: take dy/dt & dx/dt , then find dy/dx = ylogy/ax. ]
Question5
(i)differentiate: Sec-1(1/(2x2 – 1)),w.r.t.sin-1(3x –4x3).
[Hint: let u=1st fn. & v= 2nd fn. , find du/dv = 1]
(ii)differentiate: tan-1 ( ),w.r.t. sin-1 ( ) if 1<x<1;x≠0
[ du/dv= ¼, put x=tanѲ⇨ u=Ѳ/2, v=2Ѳ , u&v as assumed above-
(msin-1x)
(iii) If y = e , show that (1-x2)y2 – xy1 – m2y= 0.
Question 6 Water is driping out from a conical funnel, at the uniform rate
of 2cm3/sec. through a tiny hole at the vertex at the bottom. When the
slant height of the water is 4cm.,find the rate of decrease of the slant
height of the water given that the vertical angle of the funnel is 1200 .
[Hint: Let l is slant height ,V = 1/3. .l( /2)2.l/2= l3/8(vertical angle will
be 600 (half cone), take dv/dt=-2cm3/sec. ⇨l=-1/3 cm/s.]
**Question 7(i) Let f be differentiable for all x. If f(1)=-2 and if f `(x) ≥2 ∀
x∊[1, 6], then prove f(6) ≥8.[ use L.M.V.Thm.,f`(c)≥2,c∊[1, 6]]
(ii) If the function f(x)= x3 – 6x2+ax+b defined on [1, 3] satisfies the
rolle’s theorem for c = (2 +i)/ , then p.t. a = 11 & b∊R.
[Hint: Take f(1)=f(3) , use rolle’s thm. f`(c)=0⇨ a=11]
Question 8 (i) Show that f(x)= x/sinx is increasing in (0, п/2)

32. *HINT: f’(x)>0 , tanx >x+
(ii) Find the intervals of increase and decrease for f(x) = x3 + 2x2 – 1.
[Answer is increasing in (-∞, -4/3)U(0, ∞) & decreasing in (-4/3, 0)]
(iii) Find the interval of increase&decrease for f(x) =log(1+x)-(x/1+x)
OR
Prove that x/1+x < log(1+x) < x for x > 0.
[ Hint: f(x)strictly ↑ in ,0, ∞) , x>0 ⇨f(x)>f(0), let g(x)=x-log(1+x)
g(x)>0 ↑ in ,0,∞) & f(x) ↓ in (-∞, 0-.-
(iv) For which value of a , f(x)=a(x+sinx)+a is increasing.
,Hint: f’(x) a(1+cosx) ≥0 ⇨ a>0 ∵ -1≤cosx≤1-
**Question 9 Problem: Using differentials, approximate the expression
Solution: We let
Hence, x = 0.05 and y = /4.
Differentiating, we obtain
Substituting, we get
Question 10 For the curve y = 4x3 − 2x5, find all the points at which the tangents
passes through the origin.
[Hint: eqn. Of tangent at (x0,y0) , put x,y=0,(x0,y0)lies on given curve]

33. Question 11 Find the stationary points of the function f(x) = 3x4 –
8x3+6x2 and distinguish b/w them. Also find the local max. And local
mini. Values, if they exist.
* f’(x)=0⇨ x=0,1 f has local mini. At x=0∵f’’>0 & f’’(1)=0, f has point
of inflexion at x=1,f(1)=1]
Question 12 Show that the semi – vertical angle of right circular cone
of given total surface area and max. Volume is sin-1 1/3.
[Hint: take S=Пr(l+r) ⇨ l= S/пr – r , take derivative of V² OR can use
trigonometric functions for l & h]
Question 13 A window has the shape of a rectangle surmounted by an
equilateral ∆. If the perimeter of the window is 12 m., find the
dimensions of the rectangle so that it may produce the largest area of
the window.
[Hint: let x=length, y=breadth, then y=6 – 3y/2, A= XY+ X2 /4, take
derivative of A & it is max. ,x=4(6+ )/11 ,y=6(5 )/11]
ASSIGNMENT OF INTEGRATION
Question 1 Evaluate: (i)** Integrate .[ Use the power substitution
Put ]
 ** (iii) Integrate . [ Use the power substitution
 Put ]
 (iii) [answer is (2 - √2)/3 ]
(iv) ∫ dx [multiply&divide by sin(a-b)] (v) dx
[multiply & divide by ] (Vi)∫ dx [by partial fraction]
(v) dx [ use ∫ex(f(x)+f’(x))dx+ (vi) dx [put sinx=
, cosx = , then put t=tanx/2. Answer is – ]

34. (vii) dx [ + = ∫+ve dx+∫ -ve dx ,
answer is 5/2п- 1/п2] (viii) [ write sin2x = 1-cos2x answer is п/6]
(ix) + dx * answer is √2 ] (x) dx [ put x=atan2Ѳ
, answer is a/2(п-2) ] (xi) dx [ use property dx =
dx , dx = dx ∵f(2a-x) = f(x) , then put t=tanx, answer is
п²/2√2 - (xii) dx , where f(x) =|x|+|x+2|+|x+5|. [ dx +
dx , answer is 31.5 ] (xiii) Evaluate dx [use (f(x)+f’(x))dx
Question 2 Using integration, find the area of the regions: (i) { (x,y): |x-1| ≤y
≤ }
(ii) *(x,y):0≤y≤x2+3; 0≤y≤2x+3; 0≤x≤3+
[(i) A= dx- dx - dx = 5/2 [
+ ] – ½ ] [(ii) dx + dx , answer is 50/3]
(iii) Find the area bounded by the curve x 2 = 4y & the line x = 4y – 2.
[A = dx - dx = 9/8 sq. Unit.]
**(iv) Sketch the graph of f(x) = ,evaluate dx
[hint: dx = dx + dx = 62/3.]
**Question 3 evaluate dx [ mult. & divide by , put 1+x
=A.(d/dx)(x2+x)+B ,find A=B=1/2, integrate]
Definite integral as the limit of a sum , use formula : dx
, where nh=b-a & n→∞ Question 4 Evaluate
) dx (ii) dx
[ use = 1 for part (i) , use formulas of special sequences, answer is 6]

35. Some special case :
(1) Evaluate: [ put x+1=t²] (2) [ put x+1 = t² ]
(3) Evaluate: (4) Evaluate: [ put x=1/t for both]
(5) Evaluate: [ divide Nr. & Dr. By x2 , then write x²+1/x²=(x-1/x)² +2
according to Nr. , let x-1/x=t]
(6) Evaluate dx [ let x=A(d/dx) ( 1+x-x²) +B]
(7) Integrating by parts evaluate =
(8) Evaluate dx = dx [ put sinx=Ad/dx(sinx+cosx)+B(sinx+cosx)+C
If Nr. Is constant term then use formulas of sinx,cosx as Ques. No. 1 (vi) part]

36. ASSESSMENT OF DIFFERENTIAL EQUATIONS FOR CLASS—
XI Level--1
Q.1 Find the order and degree of the following differential equations.
State also whether they are linear or non-linear.
(i) X2( )3 + y ( )4 y4 =0. (ii) = .
Q.2 Form the differential equation corresponding to y2 = a (b – x)(b+ x)
by eliminating parameters a and b.
Q.3 Solve the differential equation (1+e2x) dy + (1+y2) ex dx = 0, when
x= 0, y =1.
Q.4 Solve the differential equation: = .
Q.5 Verify that y = A cosx – Bsinx is a solution of the differential
equation + y = 0.
Answers of Level—1
1. (i) order =2 , degree=3 , non linear( because degree is more than 1 )
, (ii) order 2 , degree 3 , non-linear .
2. y2 = a(b – x)(b+ x) = a (b2 – x2), 2y =-2ax ⇨ y = -ax, again
differentiate Y + )2 = -a , by using the value of a from above
step , we will get , x{ Y + )2 } = y .
3. = - , Integrating both sides, we get
=-∫ , put ex = t⇨ =- +c
Using x=0, y=1, we have y = 1/ex.
4. y = 2 tan(x/2) – x +c , put tan(x/2) =
5. = - A sinx – B cosx , = - A cosx + B sinx = -y.
Level---2

37. Q.1 Solve: y dx + x log ( ) dy – 2x dy = 0 .
Q. 2 Which of following transformations reduce the differential
equation + = into the form
+ P(x) u = Q(x) ?
(i) u = (ii) u = ex (iii) u = -1
(iv) u = 2
Q.3 Solve: +xy = xy3
Q.4 Solve: = +
Q.5 Solve: +x = x3 cos2y
Answers of Level ---2 1. put x = vy , answer = 1+ log ( ) = ky .
2. (iii) differentiate w.r.t. x = - . , put the value of in
the given differential equation. 3. put = t, answer is =1+c . 4.
put x+y = v, answer is = x + c.
5. put tan y = v, I.F. = , also use = 2siny cosy.
ASSESSMENT OF PROBABILITY FOR CLASS –XII
Level—1
Q. 1 If the mean and variance of a binomial distribution are 4 and 4/3
respectively, find P(X 1).
Q. 2 If P(A) = 3/8 , P(B) = ½ and P(A∩B) = ¼ , find P( / ).
Q.3 A bag contains 4 white and 2 black balls. Another bag contains 3
white and 5 black balls.
If one ball is drawn from each bag, find the probability that
(i) Both are white balls.
(ii) One is white and one is black.
Q.4 If A and B are independent events and P(A∩B) = 1/8, P( A’ ∩ B’)
=3/8 , find P(A) and P(B).

38. Q.5 The probabilities of P, Q and R solving a problem are ½, 1/3 and ¼
respectively. If the problem is attempted by
all simultaneously, find the probability of exactly one of them
solving it.
Answers of Level—1 Ans.1 np = 4, npq = 4/3 ⇨ q=1/3 ⇨ p = 1 - 1/3
= 2/3 ⇨ n=6 ⇨ P(X 1) =1 – C(6,0) (2/3)0 (1/3)6 = 1 - = .
Ans.2 P( / ) = P( ∩ ) /P(B) = = = ¾.
Ans.3 (i) P(A ∩ B) = P(A).P(B) = (2/3).(3/8) [A,B are independent
events] (ii) P(A’ ∩ B) + P(A ∩ B’) = P(A’).P(B)+P(A).P(B’) =( 1/3).(3/8)+
(2/3).(5/8)=13/24. *A’, B are indep. Events, B’ A are indep. events+,
where A = drawing a white ball from first bag. B= drawing a same ball
from second bag.A’ = drawing a black ball from first bag and B’
=drawing from second bag. Ans.4 P(A∩B) = P(A).P(B) = 1/8 let x=P(A),
y= P(B), P( A’ ∩ B’) =3/8 = P( A’) .P( B’) =(1- X)(1 – Y) ⇨ X+Y – XY = 5/8 ⇨
X=1/2 , Y= ¼.
Ans. 5 P(A’)=1/2 ,P(B’) = 1-1/3=2/3 , P(C’)=3/4 ∴ Req. Prob. =
P(A)P(B’)P(C’) = P(A’)P(B)P(C’)+ P(A’)P(B’)P(C) *A,B,C are indep. events+
= (1/2)(2/3)(3/4)+(1/2)(1/3)(3/4)+(1/2)(2/3)(1/4)=11/24.
Level---2
Q.1 If A ∩ B = ф, show that P(A/B) =0, where A and B are possible
events.
Q.2 A pair of dice is thrown if the sum is even, find the probability that
at least one of the dice Shows three.
Q.3 Let X denotes the number of hours you study during a randomly
selected school day.The probability that X can take the value x, has the
following form, where k is some unknown constant P(X=0)=0.1 and
P(X=x) =

39. (i) Find k. (ii) What is the probability that you study at least two hour?
Exactly two hour? At most two hours?
Q.4 Six dice are thrown 729 times. How many do you expect at least
three dice to show a 5 or 6?
Q.5 In a class; 5% of the boys and 10% of the girls have an I.Q. of more
than 150. In this class 60% of the students are boys. If a student is
selected at random and is formed and is found To have an I.Q. of more
than 150, find the probability that the student is a boy.
Answers of Level—2
Ans.1 A and B are possible events ⇨A ≠ ф⇨ P(A)≠ 0 , P(B) ≠0 But
A∩B = ф ⇨ P(A∩B) = P(ф) = P(A/B) = =0. Ans. 2
n(S)=36, n(A)=18 Out of these 18, the cases which at least one die
shows up 3 are (1, 3),(3,1),(3,3),(3,5),(5,3) Required
probability=5/18. Ans.3
X 0 1 2 3 4
P(X) 0.1 K 2K 2K K
(i) k=0.15 (ii) 0.75, 0.3, o.55.
Ans.4 P(success)= 2/6=1/3 ∴ q=2/3
P(x success i.e., getting a 5 or 6)= C(6, x) Px q6-x P(at least three
successes in six trials) = P(x≥3)=1 – [p(0)+p(1)+p(2)]
By using above result we get 1 – (16/81)(31/9) = 233/729 ∴
required answer is 233/729x729=233. Ans.5 Let E1: The student
chosen is a boy. P(E1)=60/100 ∴ E2: ........................................girl. P(E2)
= 40/100 E1, E2 are mutually exclusive. A: a student has an I.Q. of
more than 150. P(A/ E1)= 5/100, P(A/ E2)= 10/100 By Baye’s
theorem P(E1/A) = 3/7.