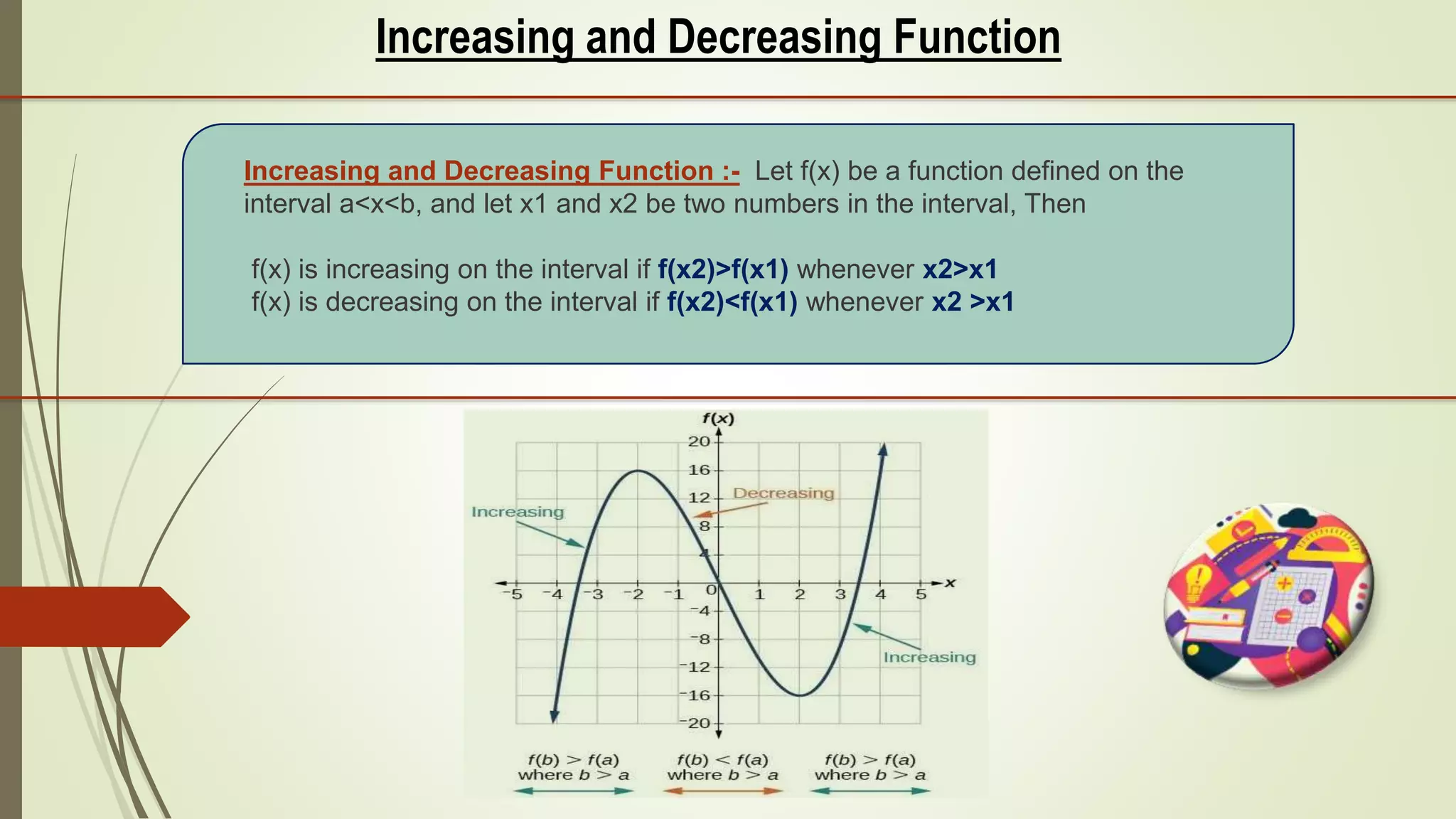
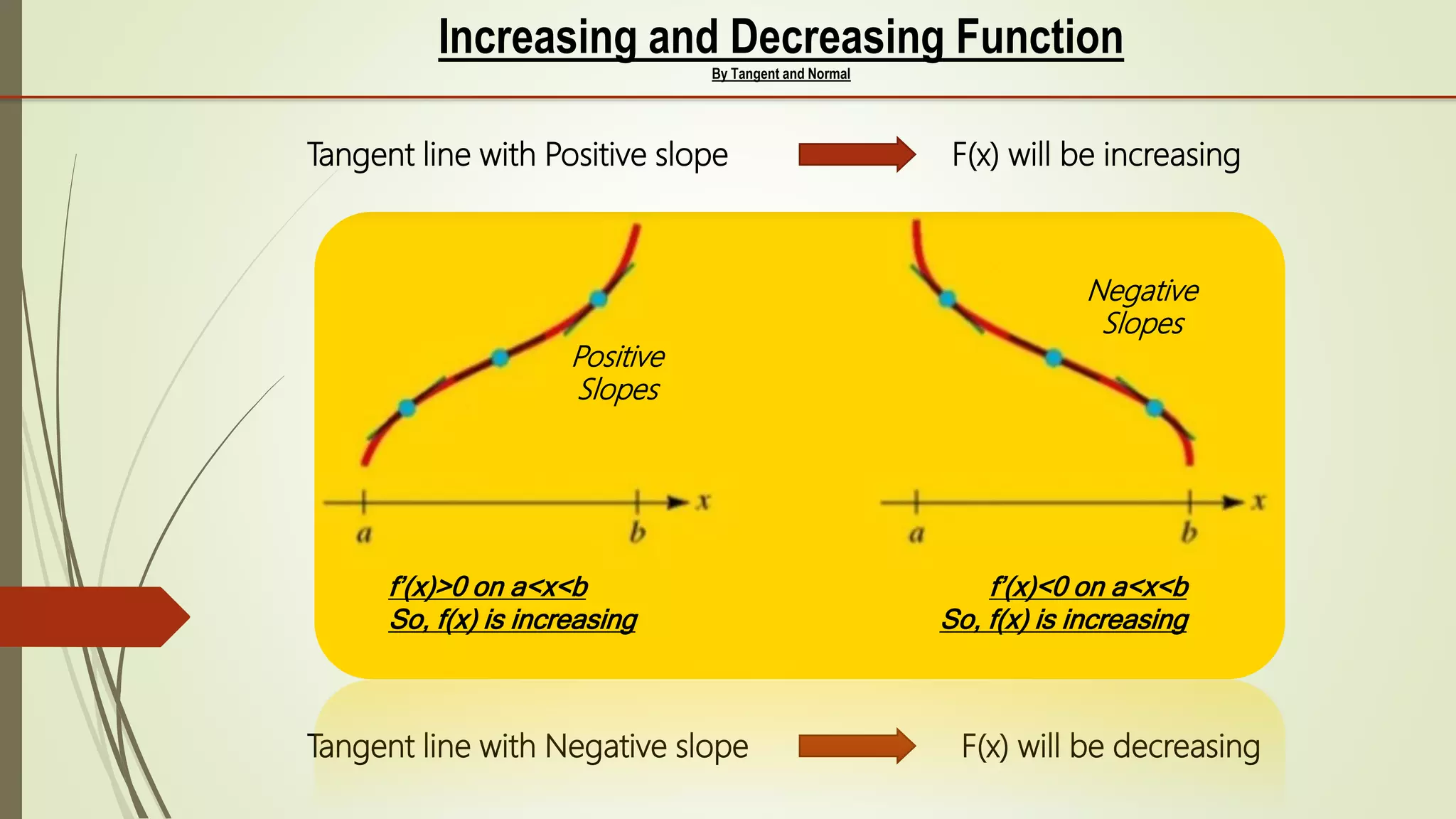
The document discusses the applications of derivatives, explaining that the derivative represents the rate of change and the slope of a curve. It highlights real-life uses in areas such as automobiles, radar guns, and business for estimating profit and loss. It also covers the concepts of increasing and decreasing functions, as well as local maxima and minima in the context of calculus.

1. NALANDA ENGLISH MEDIUM HIGHER SEC. SCHOOL
KURUD BHILAI (C.G.)
Session : 2020-2021
Art Integrated Learning
On
Mathematics
Topic : Applications of Derivative
Guided By :
Mrs. Saida Mam
Submitted By :
Shubham , Prem, Rajeev,
Rohit, Rounak
Class – 12th 'A’

2. With the Calculus
as a key,
Mathematics can
be successfully
applied to the
explanation of the
course of Nature
-Alfred North Whitehead
Introduction to Derivative
1. The Derivative is the exact rate at which one quantity
changes to another.
2. Geomatrically, The derivative is the slope of the curve at the
point on curve.
3. The Derivative is often called the 'Instantaneous’ rate of
change.
4. The Derivative of function represents an infinitely small
change the function with respective one of its variable

3. Real Life Applications of Derivative
• AutoMobiles - In an automobile there is always an odometer and a
speedometer. These two gauges work in tandem and allow the driver
to determine his speed and his distance that he has traveled.
• Radar Guns - The gun is able to determine the time and distance at
which the radar was able to hit a certain section of your vehicle.
• Business - You can estimate the profit and loss point for certain
ventures.
• Graphs - The most common application of derivative is to analyze
graphs of data that can be calculated from many different fields. Using
derivative one is able to calculate the gradient at any point of a graph.

4. Increasing and Decreasing Function
Increasing and Decreasing Function :- Let f(x) be a function defined on the
interval a<x<b, and let x1 and x2 be two numbers in the interval, Then
f(x) is increasing on the interval if f(x2)>f(x1) whenever x2>x1
f(x) is decreasing on the interval if f(x2)<f(x1) whenever x2 >x1

5. Increasing and Decreasing Function
By Tangent and Normal
Tangent line with Positive slope F(x) will be increasing
Tangent line with Negative slope F(x) will be decreasing
Positive
Slopes
Negative
Slopes
f’(x)>0 on a<x<b
So, f(x) is increasing
f’(x)<0 on a<x<b
So, f(x) is increasing

6. Local Maxima and Local Minima
Relative Local Extrema :
A function f(x) has a relative local maximum value at an interior point c of
its domain if f(x) ≤ f(c) for all x in some open interval containing c.
A function f(x) has a relative local minimum value at an interior point c of
its domain if f(x) ≥ f(c) for all x in some open interval containing c.

7. ThankYou
Submitted By :-
Shubham Prasad , Prem raj Singh, Rohit Gupta,
Rajeev Sahu, Rounak Kumar
Class 12th A