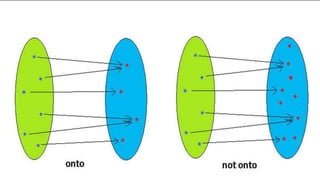
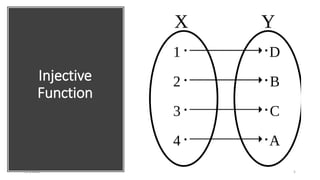
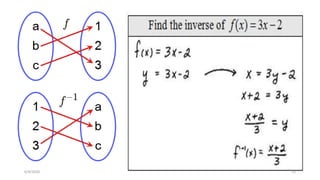
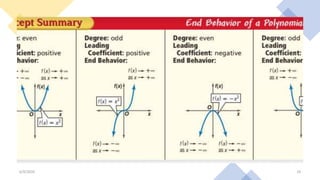
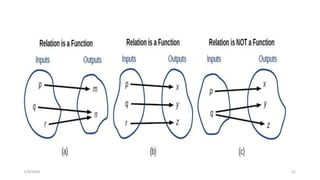
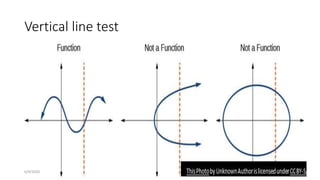
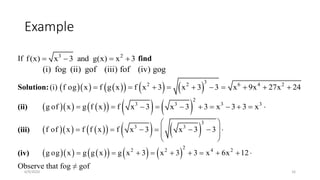The document discusses different types of functions including: 1) Surjective functions where the range equals the co-domain. 2) Injective functions where distinct inputs have distinct outputs. 3) Bijective functions which are both injective and surjective. It also discusses even and odd functions, inverses, composites, and examples of calculating different functions.

1. Chapter One
Topic 02
TYPES OF FUNCTION
BY SANAULLAH MEMON
6/9/2020 1

2. • Types of functions
• Even odd functions
• Inverse function
• Algebra of function
• Composite function
6/9/2020
2

3. Types of Functions
• Surjective Function(onto function)
Let, f: x Y
𝑅𝑓=Y (RANGE OF FUNCTION EQUALS CO-DOMAIN)
f(x) = x3
from R to R is onto,
f(x)=x2
isnotontobecauseY≠R..
6/9/2020 3

4. 6/9/2020 4

5. Injective
Function
6/9/2020 5

6. Injective or one-one function
A function f from set X to set Y is said to be an Injective if distinct elements of fD have
distinct images, that is, if for all 1 2 fx ,x D :
1 2 1 2x x f(x ) f(x )  
An Injective function is also known as One–One function
y = f(x) = x3
from R to R is one–one because different values of x have different images
in f(x).
The function f(x) = x2
from R to R on the other hand, is not one–one because different
values of x have the same image
6/9/2020 6

7. Bijective Function:
• A function f from R to R is both Injective and Surjective then f is called bijective
• function f(x) = x3 is Bijective function.
6/9/2020 7

8. 6/9/2020 8

9. 6/9/2020 9

10. Even and Odd Functions
• y = f(x) Even f(-x) = f(x) odd f(-x) = - f(x).
If a function does not satisfy these conditions, it is said to be neither
even nor odd function
For example, the function f(x) = x2
+ 1 is even function, for
f(-x) = (-x)2
+ 1 = x2
+ 1 = f(x)
The function f(x) = x3
+ x is odd function because
f(-x) = (-x)3
+ (-x) = - x3
– x = - (x3
+ x) = - f(x).
The function f(x) = x3
– x is neither even nor odd function.
6/9/2020 10

11. Inverse of a Function
Let y = f(x) be a function of x. We define inverse function as: x = f-1(y).
For example if: y = (x + 2)/(x – 7)  y(x – 7) = (x + 2)
 yx – x = 2 + 7y  x(y – 1) = (2 + 7y)
 x = (2 + 7y)/(y – 1)  x = f-1(y) = (2 + 7y)/(y – 1)
6/9/2020 11

12. 6/9/2020 12

13. 6/9/2020 13
REMARK: It may be noted that if y = f(x) be a function of x then its inverse x = f -1
(y)
may or may not be a function. f -1
(y) is a function only if f(x) is both 1-1 and onto, that is;
if y = f(x) is bijective function then it’s inverse x = f -1
(y) is a function and moreover, the
resultant inverse function is also bijective function.
Let us take an example:
(i) Consider y = x + 5. Since this function is bijective function hence, its inverse x
= y – 5 is also a function. In fact x = y – 5 is bijective function.
(ii) Now consider the function y = x2
. It’s inverse is x y  is not a function
because for one value of y there are exactly two values of x.

14. 6/9/2020 14
This Photo by Unknown Author is licensed under CC BY-SA

15. 6/9/2020 15

16. Example
If 3 2
f(x) x 3 and g(x) x 3    find
(i) fog (ii) gof (iii) fof (iv) gog
Solution:          
3
2 2 6 4 2
(i) f g x f g x f x 3 x 3 3 x 9x 27x 24         o
(ii)          
2
3 3 3 3
g f x g f x f x 3 x 3 3 x 3 3 x          o
(iii)          
3
3 3
f f x f f x f x 3 x 3 3
 
       
 
 
o
(iv)          
2
2 2 4 2
g g x g g x g x 3 x 3 3 x 6x 12         o
Observe that fog ≠ gof
6/9/2020 16

17. 6/9/2020 17
Algebra of Functions
Let f and g be given functions. The sum f g, the difference f g, the product f g and
the quotient f /g are functions defined by:
         f gi f g x f x g x , x D D     
         f gii f g x f x g x , x D D     
         f giii fg x f x g x , x D D   
   
 
 
 f g
f xf
iv x , x D D , g x 0
g g x
 
      
 
The reciprocal of the function f is denoted by 1 f and defined as
   
 
 f
1 1
v x , x D where f x 0
f f x
 
     
 
       fvi cf x cf x , x D , c R    

18. 6/9/2020 18
If f(x) = 2x – 1 and g(x) = x2 + 1 where x R, find
(i) (f + g) (ii) (f – g) (iii) fg (iv) 1/f
(v) f/g (vi) -3f (vii) f(x + 2) (viii) g(x – 3)
Solution:
(i)       f g x f x g x   2 2
2x 1 x 1 x 2x x(x 2) x R         
(ii)           2 2
f g x f x g x 2x 1 x 1 x 2x 2 x R            
(iii)          2 3 2
fg x f x g x 2x 1 x 1 2x x 2x 1 x R          
(iv)  
 
1 1 1
x x R,x 1/ 2
f f x 2x 1
 
     
 
(v)  
 
  2
f xf 2x 1
x , x R
g g x x 1
  
    
 
(vi) (-3f)(x) = - 3f(x) = -3(2x -1) = -6x + 3, x R 
(vii) f(x 2) 2(x 2) 1 2x 3      x R 
2 2 2
(viii) g(x 3) (x 3) 1 x 6x 9 1 x 6x 10           x R 

19. 6/9/2020 19

20. This Photo by Unknown Author is licensed under CC BY-SA-NC
This Photo by Unknown Author is licensed under CC BY-NC
6/9/2020 20

21. 6/9/2020 21

22. Vertical line test
6/9/2020 22

23. The end
23 6/9/2020
This Photo by Unknown Author is licensed under CC BY-SA-NC