The document outlines key calculus concepts including: - Functions, derivatives, differentiation rules, and the definition of a derivative as an infinitesimal change in a function with respect to a variable. - Concepts related to derivatives such as local/absolute extrema, critical points, increasing/decreasing functions, concavity, asymptotes, and inflection points. - How to use the first and second derivative tests to determine local extrema, concavity, and increasing/decreasing behavior.

1. Calculus

2. Concepts
 Properties of real numbers, exponents, and radicals
 Factoring
 Finding distance and midpoint
 Symmetry
 Properties of even and odd functions
 Slope and equation of lines
 Transformations of graphs
 Quadratic formula and equations
 Complex numbers
 Conic sections (circles, ellipses, hyperbolas, parabolas)
 Matrices
 Systems of equations and inequalities
 Exponential and logarithmic functions
 Trigonometric functions and inverse trigonometric functions

3.  Rational functions and functions involving radicals
 Asymptotes: horizontal, vertical, slant
 Graphing techniques for rational functions
 Vectors, parametric equations, and polar coordinates
 Components of a vector:
x-component = rcos(theta)
y-component = rsin(theta)
 Rectangular <--> polar conversion equations
x = rcos(theta)
y = rsin(theta)
r2 = x2 + y2
tan(theta) = y/x
 Sequences, series, and probability
 Sigma notation
 Arithmetic sequences
 Geometric sequences
 Permutations & combinations

4.  The cartesian plane and functions
 The real number line
 The cartesian plane and the distance
formula
 Lines in the plane; slope
 Circles
 Graphs of equations
 Functions
 Limits
 Limits
 Continuity
 Limits & asymptotes
 Curve sketching
 Differentiation
 The derivative as the slope of a curve
 Differentiability and continuity
 The derivative as a rate of change
 Higher order derivatives
 The product and quotient rules
 Position - velocity - acceleration
functions
 The chain rule and the general power
rule
 Implicit differentiation
 Related rates
 Applications of differentiation
 Extrema on an interval
 The mean value theorem
 Increasing and decreasing functions
 The first derivative test
 Concavity & the second derivative test
 Limits at infinity (horizontal
asymptotes)
 Curve sketching (including extrema &
concavity)
 Optimization problems (max/min
problems)
 Newton's method
 Differentials

5. Function
Let A and B be sets.
A function F:A → B is a relation that assigns to each xϵA a
unique y ϵ B. We write y=f(x) and call y the value of f at
x or the image of x under f. We also say that f maps x
to y.
The set A is called the domain of f. The set of all possible
values of f(x) in B is called the range of f. Here, we will
only consider real-valued functions of a real
variable, so A and B will both be subsets of the real
numbers. If A is left unspecified, we will assume it to
be the largest set of real numbers such that for all x ϵ
A, f(x) is real.

6. Derivative
The derivative of a function represents an infinitesimal change in the
function with respect to one of its variables.
The "simple" derivative of a function with respect to a variable is
denoted either or
(1)
often written in-line as . When derivatives are taken with respect
to time, they are often denoted using Newton's over dot notation
for fluxions,

7. Differentiation
Process of finding derivatives is
called differentiation.
Differentiation Rules

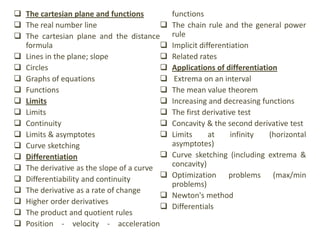
8.  d/dx c = 0, c constant
 d/dx cf(x) = cf'(x), c constant
 d/dx [f(x) ± g(x)] = f'(x) ± g'(x)
 d/dx [f(x) * g(x)] = f(x) * g'(x) + g(x) *
f'(x) (product rule)
 d/dx [f(x) / g(x)] = (g(x)f'(x) -
f(x)g'(x))/([g(x)]2) (quotient rule)
 d/dx f[g(x)] = f'[g(x)] * g'(x)
OR
for u = g(x),
 d/dx f(u) = f'(u) * u' = f'(u) * g'(x)
OR
dy/dx = dy/du * du/dx (these are all
chain rule)
 GENERAL
 d/dx un = nun-1 * u‘
 d/dx lnu = u'/u
 d/dx eu = eu * u‘
 d/dx sinu = cosu * u‘
 d/dx cosu = -sinu * u‘
 d/dx tanu = sec2u * u‘
 d/dx arcsinu = u'/(SQRT(1 - u2))
 d/dx arctanu = u'/(1 + u2)
 d/dx cotu = -csc2u * u‘
 d/dx secu = secu tanu * u‘
 d/dx cscu = -cscu cotu * u‘
 d/dx au * u' ln a
 d/dx logau = u'/(u ln a)
 SPECIFIC
 d/dx xn = nxn – 1
 d/dx lnx = 1/x
 d/dx ex = ex
 d/dx sinx = cosx
 d/dx cosx = -sinx
 d/dx tanx = sec2
 d/dx arcsinx = 1/(SQRT(1 - x2))
 d/dx arctanx = 1/(1 + x2)
 d/dx cotx = -csc2x
 d/dx secx = secx tanx
 d/dx cscx = -cscx cotx
 d/dx ax = ax ln a
 d/dx logax = 1/(x ln a)

9. Definitions
Derivatives: Min, Max, Critical Points... (Math | Calculus | Derivatives |
Extrema/Concavity/Other) Asymptotes
horizontal asymptote: The line y = y0 is a "horizontal asymptote" of f(x) if and
only if f(x) approaches y0 as x approaches + or –
vertical asymptote: The line x = x0 is a "vertical asymptote" of f(x) if and only if
f(x) approaches + or - as x approaches x0 from the left or from the right.
slant asymptote: the line y = ax + b is a "slant asymptote" of f(x) if and only if lim
(x-->+/-) f(x) = ax + b.
concave up curve: f(x) is "concave up" at x0 if and only if f '(x) is increasing at x0
concave down curve: f(x) is "concave down" at x0 if and only if f '(x) is
decreasing at x0
The second derivative test: If f ''(x) exists at x0 and is positive, then f ''(x) is
concave up at x0. If f ''(x0) exists and is negative, then f(x) is concave down at
x0. If f ''(x) does not exist or is zero, then the test fails.
critical point: a critical point on f(x) occurs at x0 if and only if either f '(x0) is zero
or the derivative doesn't exist.
Local (Relative) Extrema : local maxima: A function f(x) has a local maximum at
x0 if and only if there exists some interval I containing x0 such that f(x0) >= f(x)
for all x in I.

10. Definition of a local minima: A function f(x) has a local minimum at x0 if
and only if there exists some interval I containing x0 such that f(x0) <= f(x)
for all x in I.
Occurrence of local extrema: All local extrema occur at critical
points, but not all critical points occur at local extrema.
The first derivative test for local extrema: If f(x) is increasing (f '(x) > 0)
for all x in some interval (a, x0] and f(x) is decreasing (f '(x) < 0) for all x in
some interval [x0, b), then f(x) has a local maximum at x0. If f(x) is
decreasing (f '(x) < 0) for all x in some interval (a, x0] and f(x) is increasing
(f '(x) > 0) for all x in some interval [x0, b), then f(x) has a local minimum
at x0.
The second derivative test for local extrema: If f '(x0) = 0 and f ''(x0) >
0, then f(x) has a local minimum at x0. If f '(x0) = 0 and f ''(x0) < 0, then f(x)
has a local maximum at x0.

11. Absolute Extrema
Definition of absolute maxima: y0 is the "absolute maximum" of f(x) on I if
and only if y0 >= f(x) for all x on I.
Definition of absolute minima: y0 is the "absolute minimum" of f(x) on I if and
only if y0 <= f(x) for all x on I.
The extreme value theorem: If f(x) is continuous in a closed interval I, then f(x)
has at least one absolute maximum and one absolute minimum in I.
Occurrence of absolute maxima: If f(x) is continuous in a closed interval
I, then the absolute maximum of f(x) in I is the maximum value of f(x) on all
local maxima and endpoints on I.
Occurrence of absolute minima: If f(x) is continuous in a closed interval I, then
the absolute minimum of f(x) in I is the minimum value of f(x) on all local
minima and endpoints on I.
Alternate method of finding extrema: If f(x) is continuous in a closed interval
I, then the absolute extrema of f(x) in I occur at the critical points and/or at
the endpoints of I.
(This is a less specific form of the above.)

12. Increasing/Decreasing Functions
Definition of an increasing function: A function f(x) is "increasing" at a point
x0 if and only if there exists some interval I containing x0 such that f(x0) > f(x)
for all x in I to the left of x0 and f(x0) < f(x) for all x in I to the right of x0.
Definition of a decreasing function: A function f(x) is "decreasing" at a point
x0 if and only if there exists some interval I containing x0 such that f(x0) < f(x)
for all x in I to the left of x0 and f(x0) > f(x) for all x in I to the right of x0.
The first derivative test: If f '(x0) exists and is positive, then f '(x) is increasing
at x0. If f '(x) exists and is negative, then f(x) is decreasing at x0. If f '(x0) does
not exist or is zero, then the test tells fails.
Inflection Points
Definition of an inflection point: An inflection point occurs on f(x) at x0 if and
only if f(x) has a tangent line at x0 and there exists and interval I containing x0
such that f(x) is concave up on one side of x0 and concave down on the other
side.