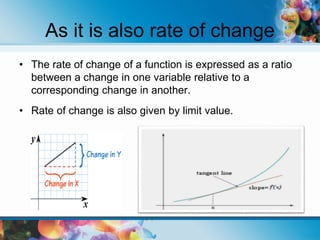
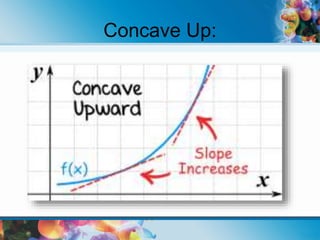
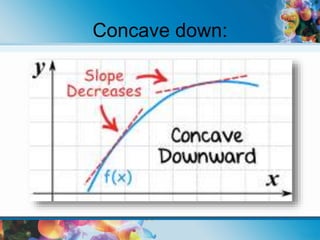
This document explains derivatives, their definitions, and applications in mathematics, detailing concepts such as differentiation, the average rate of change, and various notation forms. It covers rules for derivatives like the product rule, quotient rule, power rule, and chain rule, as well as higher derivatives and partial derivatives. Additionally, it highlights real-life applications of derivatives in fields like physics, chemistry, and economics.

1. Derivatives &
their Applications
Mathematics Presentations

2. What is derivative?
• The derivative of a function of a real variable measures
the sensitivity to change of a quantity (a function or
dependent variable) which is determined by another
quantity (the independent variable).
• For example, the derivative of the position of a moving
object with respect to time is the object's velocity: this
measures how quickly the position of the object changes
when time is advanced.

3. What is differentiation?
• The process of finding a derivative is
called differentiation.
• The reverse process is called antidifferentiation.
• The fundamental theorem of calculus states that
antidifferentiation is the same as integration.
• Differentiation is also known as the process to find rate
of change
• Derivative tells us slope of function at any point.

4. As it is also rate of change
• The rate of change of a function is expressed as a ratio
between a change in one variable relative to a
corresponding change in another.
• Rate of change is also given by limit value.

5. Average rate of change
• The Average Rate of Change is defined as
the ratio of the difference in the function f(x)
as it changes from 'a' to 'b' to the difference
between 'a' and 'b'. The average rate of
change is denoted as A(x).
• And is given as the formula
• A(x) =
𝑓 𝑏 −𝑓(𝑎)
𝑏−𝑎
• The Average Rate of Change Formula
calculates the slope of a line or a curve on a
given range.

6. Average rate of change-Ex
Calculate the average rate of change of a function, f(x) = 3x + 5
as x changes from a to b ?
Solution:
Given,
f(x) = 3x + 5 a = 3 , b = 6
Putting the values
f(3) = 3(3) + 5 :f(6) = 3(6) + 5
f(3)=14 : f(6)=23
The average rate of change is,
A(x) =
𝒇 𝒃 −𝒇 𝒂
𝒃−𝒂
A(x) =
𝟐𝟑−𝟏𝟒
𝟑
=
𝟗
𝟑
A(x) = 3

7. Notations for derivatives
Leibniz's notation.
𝒅𝒚
𝒅𝒙
,
𝒅𝒇
𝒅𝒙
x
Lagrange's notation.
f’ f”
Euler's notation.
𝑫𝒙𝒀 𝑶𝒓 𝑫𝒙𝑭(𝒙)

8. Derivative Notation
A Function
f(x)
y
X2 + 1
Newton Form
f ’(x)
y ’
(X2 + 1)’
Leibniz Form
(f(x))
(y)
(X2 + 1)
d
dx
d
dx
d
dx
or
or
df
dx
df
dx
Derivative Notation

9. Notation
There are lots of ways to denote the derivative of a function
y = f(x).
f’(x) the derivative of f
the derivative of f with
y’ y prime respect to x.
the derivative of y the derivative of f at x
with respect to x.
dx
dy
dx
df
)(xf
dx
d

10. Rules for derivatives

11. Rules for derivatives

12. Rules for derivatives

13. Rules for derivatives

14. Rules for derivatives

15. Product Rule Example

16. Examples
Product rule:
• This is used when differentiating a product of
two functions.
Differentiate x(x² + 1)
• let u = x and v = x² + 1
•
𝑑𝑢
𝑑𝑥
= 1
𝑑𝑣
𝑑𝑥
= 2𝑥

17. Examples
Product rule:
𝒅 𝒖𝒗
𝒅𝒙
=
𝒗𝒅𝒖
𝒅𝒙
+
𝒖𝒅𝒗
𝒅𝒙
Putting the values.
=(x² + 1) + x(2x)
= x² + 1 + 2x²
= 3x² + 1 .

18. Quotient Rule Example

19. Examples
Power Rule:
"what is the derivative of 𝒙 𝟔
?"
• We can use the Power Rule, where n=6:
• 𝑥 𝑛
= 𝑛𝑥 𝑛−1
• So,
• 𝑥6
= 6𝑥6−1
= 6𝑥5

20. Chain rule
A special rule, the chain rule, exists for
differentiating a function of another function.
In order to differentiate a function of a function,
y = f(g(x)),
That is to find
𝑑𝑦
𝑑𝑥
, we need to do two things:
1. Substitute u = g(x). This gives us y = f(u)
Next we need to use a formula that is known as the
Chain Rule.
2. Chain Rule
𝒅𝒚
𝒅𝒙
=
𝒅𝒚
𝒅𝒖
×
𝒅𝒖
𝒅𝒙

21. Chain Rule Example
Chain rule:
If 𝑦 = 3 2𝑥 − 1 2 𝑢 = 2𝑥 − 1
• Find
𝑑𝑦
𝑑𝑥
Solution:
𝑦 = 3 2𝑥 − 1 2
, 𝑦 = 3 𝑢 2
• Taking derivative to both side
𝒅𝒚
𝒅𝒖
= 6𝑢 -------(i
𝑢 = 2𝑥 − 1
• Taking derivative to both side
𝒅𝒖
𝒅𝒙
= 2

22. Chain rule:
• Using chain rule
•
𝑑𝑦
𝑑𝑥
=
𝑑𝑦
𝑑𝑢
.
𝑑𝑢
𝑑𝑥
•
𝑑𝑦
𝑑𝑥
= 6𝑢. 2
• = 12u
∴ 𝑢 = 2𝑥 − 1
=12(2x-1)
=24x-12
Chain Rule Example

23. Chain Rule Example

24. Higher derivatives. 1st ,2nd 3rd
• Any derivative beyond the first derivative can be referred
to as a higher order derivative.
• The derivative of the function f(x) may be denoted by
f’(x)
• Its double (or "second") derivative is denoted by f ’’(x).
• This is read as "f double prime of x," or "The second
derivative of f(x)."

25. Higher derivatives. Notations:
Let f(x) be a function in terms of x. The following are
notations for higher order derivatives.

26. 2nd Derivative Ex.

27. Higher Order Derivative Ex.

28. Partial derivatives
Partial derivatives are defined as derivatives of a function
of multiple variables when all but the variable of interest are
held fixed during the differentiation

29. Partial derivatives:
 The partial derivative of f is with respect to its
variable.
 Here ∂ is a rounded d called the partial
derivative symbol. To distinguish it from the
letter d, ∂ is sometimes pronounced "der", "del",
or "partial" instead of "dee"

30. Example

31. Applications of partial derivatives:
• Derivatives are constantly used in everyday life
to help measure how much something is
changing. They're used by the government in
population censuses, various types of sciences,
and even in economics..

32. Applications of partial derivatives:
• Derivatives in physics.
You can use derivatives a lot in Newton law of motion
where the velocity is defined as the derivative of the
position over time and the acceleration, the derivative of
the velocity over time.
• Derivatives in chemistry.
One use of derivatives in chemistry is when you want to
find the concentration of an element in a product.

33. Concave Up
• The derivative of a function gives the slope
• When the slope continually increases, the function is
concave upward.
• Taking the second derivative actually tells us if the slope
continually increases or decreases.
• When the second derivative is positive, the function is
concave upward.
• f ''(x) > 0 for x > 0;

34. Concave Up:

35. Concave down:
• When the slope continually decreases, the
function is concave downward.
• When the second derivative is negative, the
function is concave downward.
• f ''(x) < 0 for x < 0.

36. Concave down:

37. Derivatives of polynomials

38. Derivatives of polynomials

39. Derivative of Trigonometric
functions

40. Derivative of Trigonometric
functions

41. Derivatives of Exponential and
Logarithmic Functions

42. Derivatives of Exponential and
Logarithmic Functions

43. • Thank You So much for Listening
• Any Question?