The document defines the derivative of a function and discusses: - The definition of the derivative as the limit of the slope between two points as they approach each other. - Notation used to represent derivatives, including f'(x), dy/dx, and df/dx. - How the graph of a function's derivative f' relates to the graph of the original function f - where f' is positive/negative/zero corresponds to parts of f that are increasing/decreasing/at an extremum. - How to graph f given a graph of its derivative f' by sketching the curve that matches the behavior of f' at each point. - One-sided derivatives at endpoints of functions defined

1. 3.1 Derivative of a Function
What you’ll learn
•Definition of a derivative
•Notation
•Relationships between the graphs of f and f’
•Graphing the derivative from data
•One-sided derivatives
Why? The derivative gives the value of the slope of the tangent
line to a curve at a point – rate of change!

2. ( ) ( )
0
lim
h
f a h f a
h→
+ −
is called the derivative of at .f a
We write: ( )
( ) ( )
0
lim
h
f x h f x
f x
h→
+ −
′ =
“The derivative of f with respect to x is …”
There are many ways to write the derivative of ( )y f x=
→

3. What is a Derivative?
In chapter 2 we defined the slope of the curve y=f(x) at the point where
x = a to be
When it exists, this limit is called “the derivative of f at a.” Now we will
look at the derivative as a function derived from f by considering the
limit (slope) at each point of the domain of f.
The derivative of the function f with respect to the variable x is the
function f’ whose value at x is
Provided the limit exists.
h
afhaf
h
)()(
0
lim −+
→
h
xfhxf
h
xf
)()(
0
lim
)('
−+
→
=

4. 2
3y x= −
( ) ( )2 2
0
3 3
lim
h
x h x
y
h→
+ − − −
′ =
2 2 2
0
2
lim
h
x xh h x
y
h→
+ + −
′ =
2y x′ =
0
lim2
h
y x h
→
′ = +
0
→

5. A function is differentiable if it has a
derivative everywhere in its domain. It
must be continuous and smooth.
Functions on closed intervals must have
one-sided derivatives defined at the end
points.
π

6. Use the definition of derivative to find the
derivative of f(x) = x2
.
h
xfhxf
h
xf
)()(
0
lim
)('
−+
→
=

7. Derivative at a Point
The derivative of the function f at the point
x = a is the limit
Provided the limit exists.
ax
afxf
ax
xf
−
−
→
=
)()(lim
)('

8. Differentiate f(x) = x
ax
afxf
ax
xf
−
−
→
=
)()(lim
)('

9. Notation
There are lots of ways to denote the derivative of a function y = f(x).
f’(x) the derivative of f
the derivative of f with
y’ y prime respect to x.
the derivative of y the derivative of f at x
with respect to x.dx
dy
dx
df
)(xf
dx
d

10. dx does not mean d times x !
dy does not mean d times y !
→

11. dy
dx does not mean !dy dx÷
(except when it is convenient to think of it as division.)
df
dx
does not mean !df dx÷
(except when it is convenient to think of it as division.)
→

12. (except when it is convenient to treat it that way.)
( )
d
f x
dx
does not mean times !
d
dx
( )f x
→

13. Relationship between the graphs of f and f’
When we have a formula for f(x), we can derive a formula for f’(x) using
methods like examples 1 & 2. Because we think of the derivative at
a point in graphical terms as slope, we can get a good idea of what
the graph of the function f’ looks like by estimating the slopes at
various points along the graph of f.
How?
Draw the axis, marking the horizontal axis as x-units and the vertical
axis as slope units.
Estimate the slope of the graph of f(x) at various points, plotting the
slope values using the new axis.
Connect the plotted points with a smooth curve.

14. ( )y f x=
( )y f x′=
The derivative
is the slope of
the original
function.
The derivative is defined at the end points
of a function on a closed interval.
→

15. Comparison: f and f’
Graph of f
• Increasing
• Decreasing
• Maximum or minimum
value
(when slope = 0)
Graph of f’
• Positive
(above x axis)
• Negative
(below x axis)
• Zero

16. You try: Graphing f from f’
Sketch the graph of a function f that has the following properties:
i) f(0) = 0
ii) The graph of f’, the derivative of f, is shown in F 3.4
iii) F is continuous for all x.
If f ’ is constant, f will be linear with that slope.
If f ’ is discontinuous, f is not differentiable at that point.
Anywhere f ’ is positive, f is increasing.
Anywhere f ’ is negative, f is decreasing.
Anywhere f ’=0, f has a maximum or minimum value.

17. Homework
p105 1-19(odds), 14, 16

18. Opener
p108 Exercises 36-41
No Calculator!

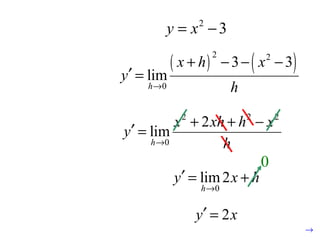
19. Graphing the Derivative from Data
You are given a table of data.
Create a second table, finding the slopes
between each data points.
Plot f’(x) by plotting your points
(midpoint between 2 data points, slope at midpoint)
])/[],([ 21 xyxx ∆∆−

20. Practice
Data Table
0 0
5 0.027
10 0.117
15 0.253
20 0.411
25 0.569
30 0.706
Estimates of slopes at
midpoints

21. One-Sided Derivatives
A function y = f(x) is differentiable on a closed interval [a,b]
if it has a derivative at every interior point of the interval
and if the right hand derivative at a and the left hand
derivative at b exist.
As with limits, if the functions right-hand and left-hand
derivatives exist and are equal at a point, then the
function is differentiable at that point.

22. One-Sided Derivatives can Differ at a Point.
Show that the following function is not
differentiable at x = 0.
0,2
0,
{
2
>
≤
=
xx
xx
y

23. Homework
page 105
Exercises 21-31 (odds)
Graph derivatives from functions
worksheet