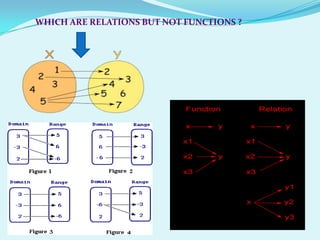
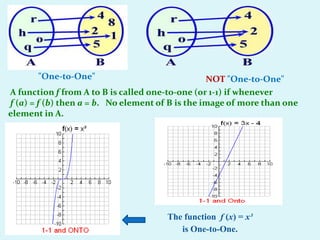
This document discusses different types of relations and functions. It defines equivalence relations, identity relations, empty relations, universal relations, one-to-one functions, onto functions, bijective functions, composition of functions, and invertible functions. It provides examples to illustrate these concepts.

1. TYPES OF RELATIONS , TYPES OF
FUNCTIONS & BINARY OPERATIONS
BY:--INDU THAKUR

2. EQUIVALENCE RELATION ON A: Let R be a
relation on a non empty set A, then R is called an
equivalence relation iff it is: (i) Reflexive , (ii) Symmetric
& (iii) Transitive.
Note: If a Relation does not satisfy any of the above
properties it is not considered as an equivalence Relation.
Identity Relation: Let A be a set. Then the relation
IA = {(a, a) for all a є A} is called the identity relation on A. In other
words a relation IA on A is called Identity Relation if every element of A
is related to itself only. Example: Let A={1,2,3} be a set.
The relation IA ={(1,1),(2,2),(3,3)} is the identity relation on set A.
But the relation R1 ={(1,1),(2,2)}and R2={(1,1),(2,2),(3,3),(1,3)} are not
identity relations on A ,
because (3, 3) ∉ R1 and in R2 element 1 is related to elements 1 and 3
as well.

3. Let A={1,2,3} be a set. Then R= {(1,1),(1,2),(2,1),(3,2)} is not a Reflexive
Relation on A. But R1= {(1,1),(2,2),(2,1),(3,2)} is not a Reflexive
Relation on A, because 2ЄA but(2,2) ∉ R.
Note: Identity Relation is always reflexive on a non-void Set.
However a Reflexive is not necessarily the Identity Relation on that
set.
EMPTY RELATION : A relation in a set A is called empty relation , if
no element of A is related to any element of A , R = φ ⊆ AXA. For
example, consider a relation R in the set A = {1,2,3}
given by R = {(a,b) : |a – b|= 8} .
UNIVERSAL RELATION : A relation in a set A is called universal
relation , if each element of A is related to every element of A , i.e., R =
AXA.
For example, consider a relation R in the set A = {1,2,3} given by
R={(a,b) : |a – b|≥ 0} .
NOTE : Both the empty relation and the universal relation
are some times called trivial relations.

4. EXAMPLE : Let A ={1,2,3} , find the number of relations on A
containing (1,2) and (1,3) which are reflexive and symmetric but not
transitive.
SOL. The smallest relation R1 on A containing (1, 2) and (1,3) which is reflexive
and symmetric but not transitive is {(1,1),(2,2),(3,3),(1,2),(2,1),(1,3),(3,1)}. We are
left with two pairs (2,3) and (3,2). Now to get another relation R2 , if we add any
pair , say (2,3) to R1 then we must add the remaining pair (3,2) in order to
maintain symmetric of R2 and then R2 becomes transitive also. Hence , the number
of relation is one.
EXAMPLE : Let A ={1,2,3} , find the number of equivalence
relations on A containing (1,2) .
SOL. The smallest relation R1 on A containing (1, 2) is
{(1,1),(2,2),(3,3),(1,2),(2,1)}. We are left with two pairs (1,3),(3,1),(2,3) and (3,2).
Now to get another relation R2 , if we add any pair , say (2,3) to R1 then we must
add the remaining pair (3,2) in order to maintain symmetric of R2. Also to
maintain transitivity we are forced to add (1,3) and (3,1) thus the only bigger that
R1 is the universal relation. Hence the total number of equivalence relations on A
containing (1,2) is two.

5. EXAMPLE : Let Q be the set all rational numbers and relation on Q defined by R
={(X,Y) : 1 + XY > 0}. Prove that R is reflexive and symmetric but not transitive.
SOL. Consider any x,y Є Q , since 1+x.x = 1+x2 ≥ 1
(x,x) ЄR reflexive
Let (x,y) Є R 1+xy > 0 1+yx > 0 (y,x) ЄR symmetric.
But not transitive .
Since (-1,0) and (0,2) Є R , because 1 > 0 by putting values. But (-1,2) ∉ R because -
1<0
Greatest Integer Function (Floor or step Function)
f : R → R defined as f(x) = [x] ∀ x εR , {x} = x – [x]
where {x} is Fractional part or decimal part of x. For
Example, {3.45} = 0.45, {-2.75} = 0.25
From the definition of [x] , greatest integer less than
or equal to x we can see that
[x] = -1 for -1≤ x <0
= 0 for 0 ≤ x <1
= 1 for 1 ≤ x <2 and so on.
For smallest Integer Function (ceiling Function) ,we
take smallest integer greater than or equal to x. For
example , ⌈4.7⌉ =5 , ⌈-7.2⌉ = -7, ⌈0.75⌉ = 1 and so on.
It is neither 1-1 and onto.

6. Example : Show that the relation R defined by (a,b) R (c,d) ⇨
a+d = b+c on the set N XN is an equivalence relation.
SOL. Let (a,b) , (c,d) ,(e,f) Є NXN.
(i) reflexive : since a+b = b+a a,b Є N ⇨ (a,b) R (b,a)
(ii) symmetric : let (a,b)R(c,d) ⇨ a+d = b+c ⇨ d+a = c+b
⇨ (c,d) R (a,b) [by commutative law in N]
(iii) transitive : let (a,b) R(c,d) , (c,d) R (e,f) ⇨ a+d = b+c
and c+f = d+e by adding we will get
a+d+c+f = b+c+d+e ⇨ (a,b) R (e,f) therefore R is an
equivalence relation.
EXAMPLE: Let R be a relation on N × N, defined by (a,b) R (c,d) ad=bc
∀ (a,b) ,(c,d) Є N × N. Show that R is an equivalence relation on N × N.
SOL. Let (a,b) be an arbitrary element of N × N. Then (a,b) Є N × N.
⇨ ab = ba (by commutative on N) ⇨ R is reflexive on N × N.
Let (a,b),(c,d) Є N × N such that (a,b) R (c,d) ⇨ ad=bc ⇨ cb=da (by commutative)
Let (a,b),(c,d),(e,f) ЄN × N such that (a,b) R (c,d) and (c,d) R (e,f) then ad=bc and
cf=de ⇨(ad)(cf)=(bc)(de) ⇨ af = be ⇨ (a,b) R (e,f)

7. Example:
Find the domain of
Solution:
We set up the inequality
x2 - x - 6 > 0
and use our steps of quadratic inequalities to solve. Factoring we get
(x - 3) (x + 2) > 0
Putting -2 and 3 on a number line, gives three regions. The table shows
x+2 x-3 Total
Left (-3) - - +
Hence the solution is Middle(0) + - -
( -∞ ,-2] U [3 , ∞)
Right(4) + + +

8. WHICH ARE RELATIONS BUT NOT FUNCTIONS ?

9. The Vertical Line Test
WHAT IS THE RANGE OF ABOVE GRAPH?
If any vertical line passes through the graph at most once then
the graph is the graph of a function.

10. Example
The Circle is not the graph of a function since there are vertical lines that cross
it twice.
Horizontal line Test
If any horizontal line passes
through the graph at more than
two points then graph is not 1-1
or many one .

11. Types of functions: Let f be a function from X to Y then f is
called (i) One-one function (or injection) iff different elements of X
have different images in Y. i.e. f(x1) =f(x2) ⇨ x1 = x2 for all x1, x2
ЄX or ∀ x1≠x2 ⇨ f(x1) ≠ f(x2) .
(ii) Many-one iff two or more elements of X have same image in Y,
i.e., f is not one-one. (iii) Onto (or surjection) iff each element of Y is
the image of at least one element of X, i.e., iff range of f = Y.
(iv) Into iff there exists at least one element in Y which is not the
image of any element of X, i.e., iff range of f is a proper subset of Y.
One-one correspondence (or bijection) iff f is both one-one and
onto.

12. "One-to-One" NOT "One-to-One"
A function f from A to B is called one-to-one (or 1-1) if whenever
f (a) = f (b) then a = b. No element of B is the image of more than one
element in A.
The function f (x) = x³
is One-to-One.

13. "Onto" NOT "Onto"
(all elements in B are used) (the 8 and 1 in Set B are not used)
A function f from A to B is called onto if for all b
in B there is an a in A such that f (a) = b. All
elements in B are used.
The function g (x) = | x - 2 |
NOT One-to-One.

14. Example (i): Let f: N→N be defined by f(n) = (n + 1)/2, if n is odd Or =n/2, if
n is even for all n Є N. Examine the function is onto, one-one or bijective.
Solution: The function f is onto. Reason: Consider any nεN ( Codomain of f).
Certainly 2nεN Also 2n is even. Thus, ∀ nЄ N (co- domain of f), ⁆ 2n Є N
(domain of f) such that f(2n) = 2n/2 = n f is onto. But f is not 1-1
Reason : As 1, 2Є N (domain of f) and f (1) = (1+1)/2=1, f (2) = 2/2 = 1, so that
the different elements 1and 2 of the domain of f have the same image 1. Hence,
f is not bijective.
Example (ii): Let A=R-{3}and B=R-{1}. Consider the function f: A→B
defined by f(x) =(x-2)/(x-3).Is f one-one and onto? Justify your answer.
Solution: The function is one-one. Let x1, x2εA be such that f(x1)= f(x2)
( x1-2)/(x1-3) = (x2-2)/(x2-3) ⇨ x1x2 - 2x1 - 3x2 +6= x1x2 - 3x1 - 2x2 +6 then
-2x1-3x2 = -3x1-2x2 ⇨ x1= x2 , Hence f is one-one.
We shall find the range of the function, Let y=f(x), then y= (x-2)/(x-3)
xy-3y=x-2 then x= (3y-2)/(y-1)
but xε R.(3y-2)/(y-1)εR it implies y≠1. Range of f= R-{1}=B. Thus the range of
the function f= Codomain of f. Therefore f is onto. We can say it bijective.

15. The composition of two functions is also called the resultant of two functions
or function of a function. The function on the right acts first and the function on the
left acts second, reversing English reading order. We remember the order by
reading the notation as "g of ƒ". The order is important, because rarely do we get
the same result both ways.
Let f : A → B and g : B → C be two functions . Then the composition of f
and g , denoted by gof, is defined as the function gof : A → C given by
gof(x) = g(f(x)) , ∀ x Є A .
h = gof
Some properties of composition of functions:
1. The composition of functions is associative i.e., if f : A → B , g : B→ C ,h : C →
D are the functions then ho(gof) = (hog)of
2. Let f : A → B , g : B→ C be two functions.
(i) If f , g are both 1-1 , then gof is also 1-1.
(ii) If f , g are both onto , then gof is also onto.

16. Remark: If A and B are (non-empty) finite sets containing m and
n elements respectively, then
(i) the number of functions from A to B =nm or n(B)n(A) .
Remark : If f and g are functions such that gof is defined and
(i) If gof is 1-1 , then f and g both necessarily 1-1.
(ii) If gof is onto , then f and g both need not be necessarily onto.
It can be verified in general that gof is 1-1 implies that f is
1-1.Similarly, gof is onto implies that g is onto.
Examples : 1. f : {1,2,3,4} → {1,2,3,4,5,6} defined as f(x) = x ∀ x and
g : {1,2,3,4,5,6} → {1,2,3,4,5,6} as g(x) = x , for x=1,2,3,4
and g(5)= g(6) = 5. then gof(x)= x ∀ x , which shows that gof is 1-1 but
g is not 1-1.
2. f : {1,2,3,4} → {1,2,3,4} and g : {1,2,3,4} → {1,2,3} defined as
f(1) =1, f(2) = 2, f(3)=f(4) =3 , g(1)=1,g(2)=2 and g(3)=g(4)=3. It shows
that gof is onto but f is not onto.

17. INVERTIBLE FUNCTION: A function f : X →Y is defined
to be invertible, if there exists a function g: Y →X such
that gof = IX and fog = IY. The function g is called the
inverse of ‘f ‘ and is denoted by f –1. Thus, if f is
invertible, then f must be one-one and onto and
conversely, If f is one-one and onto, then f must be
invertible.
We state some properties of invertible functions :
1. Inverse of a bijective function is unique.
2. Inverse of a bijective function is also bijective and (f-1)-1 =f.
3. If f: A → B is bijective then (i) f-1of = IA (ii) fof-1 = IB
4. If f: A → B and g : B → C are both bijectives , then gof : A → C
and (gof)-1 = f-1og-1.
5. Let A be a non-empty set and f : A → A , g : A → A be two
functions such that gof = IA = fog then f & g are both
bijectives and g = f-1

18. Example : If f : R → R and g : R → R are given by
f(x) =|x| and g(x) = |2x – 5| , show that gof ≠ fog.
SOL. gof : R → R is given by gof(x) = g(f(x)) =
g(|x|)= |2|x| - 5| and fog : R → R is given by
fog(x) = f(g(x))= f(|2x-5|) = ||2x-5||=|2x-5| . Also
(gof) (-1) = |2|-1|-5|= |2-5|= |-3|=3 and (fog)(-1)
= |2(-1)-5| =|-7| =7 ⇨ fog ≠ gof.
Example: Show that if f: A →B and g : B →C are one-one, then gof :
A →C is also one-one.
Solution : Suppose gof (x1) = gof (x2) then g (f (x1)) = g (f (x2)) f(x1) = f (x2),
as g is one-one x1 = x2, as f is one-one Hence, gof is one-one.
Example: Show that if f: A →B and g: B →C are onto, then gof : A
→C is also onto.
Solution: an arbitrary element z Є C, ⁆ a pre-image y of z under g
such that g (y) = z, since g is onto. Further, for y Є B, ⁆ an element x in A
with f (x) = y, since f is onto. Therefore, gof (x) = g (f (x)) = g (y) = z, showing that gof
is onto.

19. BINARY OPERATIONS : Let S be a non void set. A function F
from SxS to S is called a binary operation on S. i.e. F: SxS →S is
a binary operation on set S. Generally binary operations are
represented by the symbols * , instead of letters f, g etc. Thus a
Binary operation * on a set S associates each ordered pair (a, b)
of elements of S. (or any two elements of S) to a unique
element a*b of S.

20. TYPES OF BINARY OPERATIONS:
COMMUTATIVE BINARY OPERATION :
A Binary Operation * on a set S is said to be commutative if (a*b) = (b*a) ∀ a, b є S.
ASSOCIATIVE BINARY OPERATION:
A Binary Operation * on a set S is said to be associative if (a*b)*c = a*(b*c) ∀ a, b, c є
S. DISTRIBUTIVE BINARY OPERATION:
Let * and 0 be two Binary operations on a set S. Then * is said to be
(i) Left distributive over 0 if a*(b0c) =(a*b)0(a*c) for all a, b, c є S.
(ii) Right distributive over 0 if (b0c)*a= (b*a) 0(c*a) for all a, b, c є S.
IDENTITY BINARY OPERATION:
Let * be a Binary Operation on a set S. An element e є S is said to be an
identity element for the binary operation * if a*e=a=e*a, for all a є S.
INVERSE BINARY OPERATION :
Let * be a Binary Operation on a set S. An element a є S is said to be
invertible with respect to the operation * , if ⁆ an element b in S such that
a*b= =b*a = e and b is called inverse of a.
NUMBER OF BINARY OPERATIONS: Let A be a finite set containing m
elements then the number of binary operations on A is mmxm e.g.
If A= {a, b} then the no. of binary operations on A = 24 = 16 is equal to
number of functions from A × A to A.

21. Is the operation * commutative?
(Does the property x + y = y + x hold for ALL possible arrangements of values?)
Start testing values:
a * b = b * a is true since both sides equal b.
c * d = d * c is true since both sides equal b.
WOW! Having to test ALL possible arrangements could take forever! There must
be an easier way.........
The operation * is commutative.
Testing for Commutativity Shortcut:
It is easy to check whether an operation defined
by a table is commutative.
Simply draw a diagonal line from upper left to
lower right, and see if the table is symmetric
about this line.
Reading the table: Read the first value from
This table shows the operation * the left hand column and the second value
("star"). The operation is working on from the top row. The answer is in the cell
the finite set where the row and column intersect.
A = { a, b, c, d }. The table shows the For example, a * b = b, b * b = c, c * d =
16 possible calculations using the b, d * b = a and so on.
elements of set A.

22. What is the identity element for the operation * ?
(What single element will always return the original value?)
The identity element is a.
a * a = a, b * a = b, c * a = c, d * a = d
Checking for the Identity Element:
You will know the identity element when you see it, because all of the values in its
row or column are the same as the row or column headings.
What is the inverse element for b ?
(What element, when paired with b, will return the identity element a?)
The inverse element of b is d. b*d=a
Remark : Zero is identity operation on R but it is not identity for the
addition operation on N , as 0 ∉N. In fact the addition operation on N does
not have any identity.
One further notices that for the addition operation + : R × R → R , given any
aЄR, ⁆ -a in R
such that a+(-a) = 0 (identity for ‘+’) =(-a)+a . Similarly for multiplication
operation on R , given that a ≠0 in R ,⁆ 1/a in R such that a×(1/a) = 1(identity
for ‘×’) = (1/a)×a.

23. EXAMPLE : Define a binary operation * on the set {0,1,2,3,4,5} as
a*b =
Show that 0 is the identity for this operation and each element a of the set is
invertible with 6 – a being the inverse of a.
Ans. First of all we write down the operation table.
* 0 1 2 3 4 5
0 0 1 2 3 4 5
1 1 2 3 4 5 0
2 2 3 4 5 0 1
3 3 4 5 0 1 2
4 4 5 0 1 2 3
5 5 0 1 2 3 4
From the second row of operation table it is clear that 0 is the identity
element. It is also clear that
Inverse of 1 is 5 ; inverse of 2 is 4
Inverse of 3 is 3 ; inverse of 4 is 2
Inverse of 5 is 1 ; inverse of 6 is 0 , Thus inverse of a is 6 – a.

24. Q.1 Show that the number of binary operations on {1,2}
having 1 as identity and having 2 as inverse of 2 is exactly one.
Ans.1 Binary operation on set S is a function from SXS →S i.e.,
a function from {(1,1),(1,2),(2,1),(2,2)} to {1,2}.
1*1= 1, 1*2 = 2 = 2*1, and 2*2 = 1. DIAGRAM
SXS * S
(1,1)
(1,2) 1
(2,1) 2
(2,2)
BY:--INDU THAKUR

25. Q.2 Determine the number of binary operations on {1,2}
having 1 as identity element.
Ans.2 Binary operation on set S is a function from SXS →S i.e., a
function from {(1,1),(1,2),(2,1),(2,2)} to {1,2}.
1*1 = 1, 1*2 = 2 = 2*1, and 2*2 = 1 or 2. DIAGRAM (there are
two desired binary operations on S).
SXS * S
SXS * S
(1,1) (1,1)
(1,2) 1 (1,2) 1
(2,1) 2 (2,1) 2
(2,2) (2,2)

26. EXAMPLE : Let A = NU{0} X NU{0} and let * be a binary operation on A defined by
(a,b)*(c,d) = (a+c,b+d) ∀ (a,b) , (c,d) ЄA .
Show that (i) * is commutative on A.
(ii) * is associative on A. Also ,find the identity element, if any , in A.
SOL. (i) Let (a,b) ,(c,d) ЄA
Then (a,b)*(c,d) = (a+c,b+d) and (c,d)*(a,b) = (c+a,d+b)
a+c= c+a and b+d= d+b ∀ a,b,c,d Є NU{0}
Therefore (a,b)*(c,d) = (c,d)*(a,b) ∀ (a,b) ,(c,d) ЄA
‘*’ is commutative on A .
(ii) For any (a,b) ,(c,d) ,(e,f) ЄA
{ ((a,b) *(c,d)}*(e,f) = (a+c,b+d) *(e,f)
= ((a+c)+e, (b+d)+f)
= (a+(c+e) , b+(d+f)) [by associative law on N]
= (a,b)*(c+e , d+f)
= (a,b) * { (c,d)*(e,f)} ⇨ ‘*’ is associative on A.
L et (x,y) be the identity element in A .
Then (a,b)* (x,y) = (a,b) ∀ (a,b) ЄA
(a+x , b+y) = (a,b)
a+x =a ,b+y = b , it gives x=0,y=0, therefore (0,0) ЄA (identity)
Also (0,0) *(a,b) = (0+a , 0+b) = (a,b) ∀ (a,b) ЄA.
Thus (0,0) is the identity element in A. BY:-- INDU THAKUR