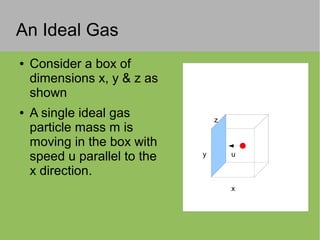
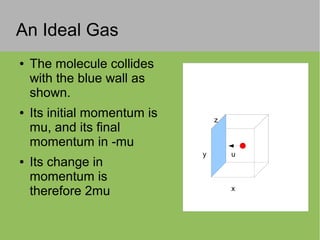
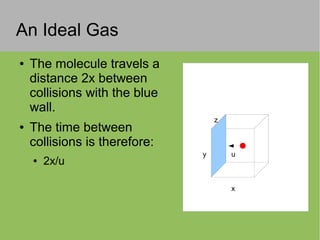
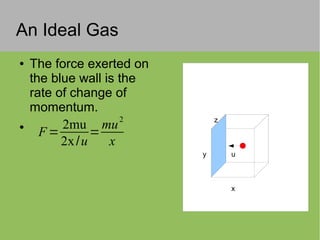
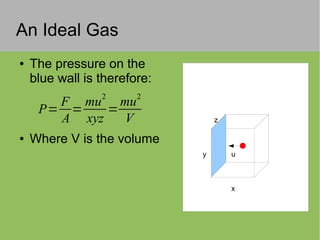
The document discusses the properties and behavior of ideal gases. It defines ideal gases as having point-like particles that exert no forces on each other except during elastic collisions. The document then derives the ideal gas law (PV=nRT) by considering the momentum transfer during particle collisions with the container walls and relating gas pressure to temperature via the kinetic energy and speeds of the particles. It concludes by noting that the ideal gas law can provide approximate descriptions of real gases.

1. Topic 3 - Thermodynamics
3.3 – The Ideal Gas

2. Gas Pressure
● Pressure is defined as the force per unit area.
● Pressure is measured in Pascals (Pa)
Gas pressure arises because of collisions
between particles (causing the force) and the wall
of the container (the area over which they act)
p=
F
A

3. An Ideal Gas
● Physicists made a set of observations of gases
from which 4 assumptions are made to define
the “ideal gas.”
● A pure gas contains identical molecules in
continuous random motion. (no one particle is more
special than another)
● All collisions are elastic (energy is conserved)
● The volume of the particles is negligible compared
to the volume of the container. (it is compressible)
● There are no forces on the molecules except during
collisions (the particles are very far apart)

4. An Ideal Gas
● Consider a box of
dimensions x, y & z as
shown
● A single ideal gas
particle mass m is
moving in the box with
speed u parallel to the
x direction.
x
z
y u

5. An Ideal Gas
● The molecule collides
with the blue wall as
shown.
● Its initial momentum is
mu, and its final
momentum in -mu
● Its change in
momentum is
therefore 2mu x
z
y u

6. An Ideal Gas
● The molecule travels a
distance 2x between
collisions with the blue
wall.
● The time between
collisions is therefore:
● 2x/u
x
z
y u

7. An Ideal Gas
● The force exerted on
the blue wall is the
rate of change of
momentum.
●
x
z
y u
F=
2mu
2x/u
=
mu
2
x

8. An Ideal Gas
● The pressure on the
blue wall is therefore:
● Where V is the volume
x
z
y u
P=
F
A
=
mu
2
xyz
=
mu
2
V

9. An Ideal Gas
● In a real gas there are N
molecules moving
randomly. On average
only 1/3 of these move in
the x direction.
● The molecules are not all
moving with speed u but
have an average (mean
square) speed <c2
>
x
z
y u
pV =
1
3
N m 〈c
2
〉

10. Molecular Speed
● For one mole of gas, the equation becomes:
● This could be written as:
● Where ½ m<c2
> is the average kinetic energy
pV =
1
3
N A m 〈c2
〉
pV =
2
3
N A×
1
2
m〈c
2
〉

11. Molecular Speed
● From other macroscopic experiments it can be
shown that:
● These two equations for ideal gases must
equate.
● Therefore:
pV =nRT
nRT =pV =
2
3
NA
1
2
m〈c
2
〉
1
2
m〈c
2
〉=
3
2
R
N A
T

12. Molecular Speed
● The ratio of the two constants (R over NA
) is
known as the Boltzmann constant k
● k=1.38 x 10-23
JK-1
● That is Kinetic Energy is proportional to
absolute temperature
1
2
m〈c2
〉=
3
2
k T

13. Summary of Ideal Gases
● For a real gas, the ideal gas rules can be used to give
approximate answers.
● An increase in volume will cause a longer time between
collisions, so the collisions will be less frequent, so the
pressure will decrease.
● An increase in temperature, will cause a higher KE, so the
time between collisions will increase and the force with
which they strike the container will increase. The pressure
will therefore increase.
● An increase in volume at constant pressure will cause the
particles to slow down, therefore causing a decrease in
temperature.