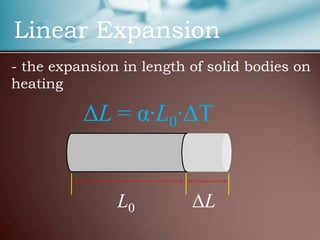This document discusses thermal expansion, which is the change in dimensions of materials due to changes in temperature. It defines linear expansion as the expansion in length and volume expansion as expansion in overall volume. The key factors that affect thermal expansion are the temperature change, material type, and original dimensions. Common materials and their coefficients of thermal expansion are provided. Examples of applications like loosening tight jar lids are given. Finally, several problems involving calculating dimensional changes due to temperature changes are presented.

1. Thermal
Expansion
Linear and Volume

2. Objectives
• Define thermal expansion
• Identify the factors affecting thermal
expansion
• Solve sample problems involving
linear expansion and volume
expansion
• Cite everyday applications of the
concepts

3. Thermal Expansion
• Change in the dimension(s) of
a substance due to change in
temperature

4. Factors affecting
THERMAL
EXPANSION

5. Temperature
• Higher change in
temperature, the higher the
expansion
• ΔT for the symbol

6. Kind of Material
• Quantified by a constant value
for coefficient of thermal
expansion for some materials
• The higher the coefficient, the
higher the expansion
• Symbol used - α

7. Original Dimension
• Greater original dimension,
greater the expansion.
• L for linear
• A for area
• V for volume

8. ΔL = α·L0·ΔT
Change in Coefficient of Original
dimension expansion length
Change in
temperature

9. Types of
EXPANSION

10. Linear Expansion
- the expansion in length of solid bodies on
heating
ΔL = α·L0·ΔT
L0 ΔL

11. Coefficients of
Thermal Expansion
for Some materials

12. LINEAR
MATERIAL
COEFFICIENT
GLASS 8.5
MERCURY 26
ALUMINUM 24
COPPER 17
Example: BRASS 19
IRON 11.1
α = 12 X 10-6 1/K PLATINUM 9
GOLD 14
SILVER 18
STEEL 11.0 ~ 13.0
CONCRETE 12
RUBBER 77

14. Opening a tight Jar lid

15. Volume Expansion
- sometimes called the “cubic expansion”
ΔL = 3α·L0·ΔT
or
V0
ΔL = β·L0·ΔT
or
ΔV ΔV = β·V0·ΔT

16. Exercises

17. 1. During winter, why is it
important to protect water pipes?

18. 2. Why is it
advisable to allow
telephone lines to
sag when stringing
them between
pokes in summer?

19. 3. What is the change in length of
a metal rod with an initial length
of 2 meters, a coefficient of
thermal expansion 0.00002 /K and
a temperature change of 20 K?

20. 4. Suppose you have a 0.05 L
container made of glass that is at
283 K. You raised its temperature
to 303 K. By how much will its
volume increase? (glass = 25.5
x10-6 1/K)

21. 5. A steel rail is 24.4m
long. How much does it
expand during a day
when the low
temperature is 291 K
and high temperature is
306 K? (Steel = 12 x10 1/K)
-6

22. 6. The length of a brass bar is 150
cm at 40 C. What will be its length
at 100 C?
(α = 19 x 10-6/K)

23. 7. An aluminum flag pole is
20.0 m tall on a -15 C winter’s
day. How much higher will the
flag fly from the pole on a hot
42 C summer day?

24. 8. What amount of change in
temperature did a 0.25 kg copper
metal undergo when it is initially
5.0 m long and expanded by
0.00002 m?

25. 9. A glass flask whose volume is 1000.0
cm 3 at 0.0 C is completely filled with
mercury at this temperature. When
flask and mercury are warmed to 80.0
C, 12.5 cm3 of mercury overflow.
Compute the coefficient of volume
expansion of the glass.