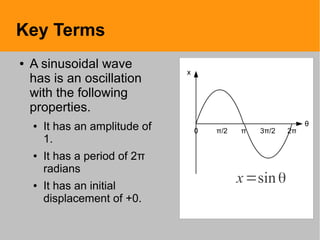
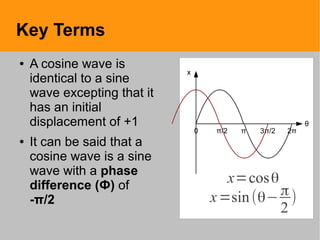
This document defines key terms and equations related to simple harmonic motion (SHM). It discusses oscillating systems that vibrate back and forth around an equilibrium point, like a mass on a spring or pendulum. The key parameters of SHM systems are defined, including amplitude, wavelength, period, frequency, displacement, velocity, acceleration. Equations are presented that relate the displacement, velocity, acceleration as sinusoidal functions of time. The concepts of kinetic, potential and total energy are also explained for oscillating systems undergoing SHM.

1. Topic 4 – Oscillations and Waves
4.1 Simple Harmonic Motion

2. Oscillations
● There are many systems, both natural and man
made, that vibrate back and forth around an
equilibrium point.
● These systems are said to regularly oscillate.
● Common examples are:
● A mass on a spring
● A pendulum
● Electrons under alternating current

3. Key Terms
● The equilibrium point is that point where the
system will naturally rest.
● e.g. for a pendulum – bottom centre
● For a mass on a spring – the point where the
upwards pull of the spring equals the downward pull
of the weight.
● The displacement (x) of the system is the
vector displacement of the system from its
equilibrium point.
● Usually the displacement is considered in 1
dimension and is given the symbol x even if the
displacement is vertical.

4. Key Terms
● The amplitude (A) of an oscillation is the
maximum displacement of the system.
● It is the height of a wave from its equilibrium point.
● It is half the peak to trough height.
● The wavelength (λ) of a moving wave is the
distance from peak to peak in the space
dimension.

5. Key Terms
● The time period (T) is the time taken in seconds to
complete 1 complete cycle.
● This is the time from peak to peak in the time
dimension.
● A cycle is complete when the system is back in its
initial state.
● e.g. for a pendulum, when the bob is at its lowest point
and travelling in the same direction as at the start.
● The frequency (f) of the system is the number of
oscillations per second.
● It is the inverse of the time period.
● Frequency is measured in Hz or s-1

6. Key Terms
● A sine wave has a period of 2π radians and a
time period of T seconds.
● Therefore its angular displacement (on an x-θ
graph) at any time is:
● The angular frequency (ω) in rad s-1
is
therefore:
θ=
2π
T
t
ω=
2π
T
=2π f

7. Questions
● Calculate the frequency and angular frequency
of:
● A pendulum of period 4s
● A water wave of period 12s
● Mains electricity of period 0.02s
● Laser light with period 1.5 fs

8. Key Terms
● A sinusoidal wave
has is an oscillation
with the following
properties.
● It has an amplitude of
1.
● It has a period of 2π
radians
● It has an initial
displacement of +0.
x
0 π/2 π 3π/2 2π
θ
x=sinθ

9. Key Terms
● A cosine wave is
identical to a sine
wave excepting that it
has an initial
displacement of +1
● It can be said that a
cosine wave is a sine
wave with a phase
difference (Ф) of
-π/2
x
0 π/2 π 3π/2 2π
θ
x=cosθ
x=sin(θ−π
2
)

10. Oscillating Systems
● An oscillating system is defined as one that
obeys the general equation:
● Here
● the amplitude is x0
● The angular frequency ensures that the real time
period coincides with the angular period of 2π
radians
● The phase allows for an oscillation that starts at any
point.
x=x0 sin(ωt+ ϕ)

11. Oscillating Systems
● If the oscillations begin at the equilibrium point
where displacement is zero at the start then:
● If the oscillations begin at the end point where
displacement is a maximum at the start then:
● This second form is more useful in more
situations
x=x0 sin(ωt)
x=x0 cos(ωt)

12. Questions
● A simple harmonic motion is initiated by
releasing a mass from its maximum
displacement. It has period 2.00s and
amplitude 16.0cm. Calculate the displacement
at the following times:
● t=0s
● t=0.25s
● t=0.50s
● t=1.00s

13. Time x v
0 0 +v0
T
/4
x0 0
T
/2 0 -v0
3T
/4
-x0 0
T 0 +v0
Oscillating Systems
● The rate of change of displacement (the speed) is
given by the gradient of the displacement curve.
● Assuming that:
● Then:
● The speed is therefore:
x=x0 sin(ωt)
v=v0 cos(ωt)

14. Questions
● A bored student holds one end of a flexible ruler
and flicks it into an oscillation. The end of the
ruler moves a total distance of 8.0cm and
makes 28 full oscillations in 10s.
● What are the amplitude and frequency of the motion
of the end of the ruler?
● Use the displacement equation to produce a table
of x and t for t=0,0.04,0.08,0.012,...,0.036
● Draw a graph of x versus t
● Find the maximum speed of the end of the ruler.

15. Oscillating Systems
● The rate of change of speed (the acceleration)
is given by the gradient of the speed curve.
● Using similar logic:
● This has a very similar form to the displacement
equation therefore:
● Note that the acceleration is:
● In the opposite direction to the displacement,
● Directly proportional to the displacement.
a=−a0 sin(ωt)
a=−
a0
x0
x

16. The SHM Equation
● Any system undergoing simple harmonic
motion obeys the relationship:
● It can be shown using calculus or centripetal
motion that
● Therefore:
a∝−x
a0=ω2
x0
a=−ω2
x

17. The SHM Equations
● For a system starting
at equilibrium
● The general SHM equation applies to all simple
oscillating systems.
a=−ω2
x
x=x0 sin(ωt)
v=ω x0 cos(ωt)
a=−ω
2
x0 sin(ωt)
● For a system starting at
maximum displacement
x=x0 cos(ωt)
v=−ω x0 sin(ωt)
a=−ω
2
x0 cos(ωt)

18. The SHM Equations
● One final equation can be formed by squaring
the speed equation.
● Because sin2
θ + cos2
θ =1
v=ω x0cos(ωt)
v
2
=ω
2
x0
2
cos
2
(ωt)
v2
=ω2
x0
2
(1−sin2
(ωt))
v2
=ω2
( x0
2
−x0
2
sin2
(ωt))
v
2
=ω
2
( x0
2
−x
2
)
v=±ω√x0
2
−x
2

19. Questions
● A body oscillates with shm decribed by:
● x=1.6cos3πt
● What are the amplitude and period of the
motion
● At t=1.5s, calculate the displacement, velocity
and acceleration.

20. Questions
● The needle of a sewing machine moves up and
down with shm. If the total vertical motion of
the needle is 12mm and it makes 30 stitches in
7.0s calculate:
● The period,
● The amplitude,
● The maximum speed of the needle tip
● The maximum acceleration of the needle tip.

21. Energy Changes
● An oscillating system is constantly experiencing
energy changes.
● At the extremes of displacement, the potential
energy is a maximum.
● Gravitational potential for a pendulum, elastic
potential for a spring
● At the equilibrium position, the kinetic energy is
a maximum

22. Kinetic Energy
● Remember that kinetic energy is given by:
● Substituting
● Gives
v=±ω √ x0
2
−x2
v
2
=ω
2
( x0
2
−x
2
)
EK =
1
2
m ω
2
( x0
2
−x
2
)
EK =
1
2
m v
2

23. Total Energy
● Remember that at the equilibrium point ALL the
energy of the system is kinetic.
● The total energy of the system ET
is therefore:
● Note that the total energy of the system is
proportional to the amplitude squared.
ET =
1
2
m ω
2
(x0
2
−0
2
)
ET =
1
2
m ω2
x0
2

24. Potential Energy
● The law of conservation of energy requires that
the total energy of an oscillating system be the
sum of the potential and kinetic energies.
●
● Therefore
1
2
mω
2
x0
2
=
1
2
mω
2
(x0
2
−x
2
)+ EP
EP=
1
2
m ω2
x2
ET =EK + EP

25. Questions
● A pendulum of mass 250g is released from its
maximum displacement and swings with shm.
If the period is 4s and the amplitude of the
swing is 30cm, calculate:
● The frequency of the pendulum
● The maximum speed of the pendulum
● The total energy of the pendulum
● The maximum height of the pendulum bob.
● The energies of the pendulum at t=0.2s.