1. The document discusses gravitational fields and the simple pendulum experiment. It describes how the period of a pendulum is affected by the mass of the bob and the length of the string. The experiment can be used to calculate the acceleration due to gravity. 2. Gravitational potential energy is introduced. Lifting an object increases its gravitational potential energy, which is defined to be zero at an infinite distance. Calculations of gravitational potential energy are shown for objects near and far from Earth. 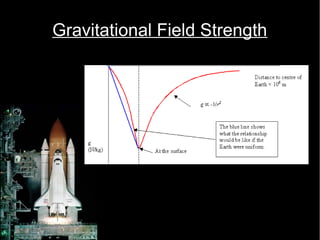3. The formula for gravitational field strength is derived, showing that it decreases with the square of the distance from the object's center. Values of g are calculated for the major planets based on their masses and radii.

1. Topic 9.2
1.1.1 Gravitational Fields

2. Mass, Weight and Gravity
 Remember that mass is a measure
of the amount of substance in an
object.
 Weight is the force of gravity pulling
down on the object's mass.
 This is expressed as the formula:
 W=mg
 What are the units of each term in this
equation?

3. The Simple Pendulum
 A simple pendulum consists of a
mass (called a bob) on a light (no
mass) string.
 The weight of the object causes it
to try to return to the lowest
position when it is disturbed.
 The time taken to make one
complete swing (Left to right to
Left) is called the TIME PERIOD, T.

4. Investigating the Simple Pendulum
 Set up a simple pendulum as
shown.
 Investigate the effect of the mass
of the bob, m, on the time period,
T, of the pendulum.
 Identify what variables need to be
controlled.
 How can you make your time
measurement as precise as possible?
 Remember keep the angle of swing
small for the best results!
 What does a graph of T against m
show?
mg
l

5. Investigating the Simple Pendulum
 Now investigate the effect of the
pendulum length, l, on the period,
T.
 Identify what variables need to be
controlled.
 How should you measure the length
of the pendulum?
 What does a graph of T against l
show?
 What does a graph of T2 against l
show?

6. Measuring g
•The time period of a simple pendulum is
given by the equation:
T = 2p l
g
•This can be written as:
2
2 = 4p
l
g
T
•Calculate g from the gradient of your T2
versus l graph.

7. Gravitational Fields
 Gravity can act over large distances,
even through space.
 To explain this we use the idea of a field.
 All objects with mass create their own
gravitational field.
 This field extends to infinity and causes
other objects to be attracted towards the
mass.
 This is similar to the electromagnetic fields.
 The gravitational field is much weaker than
the other fields.

8. Gravitational Fields

9. Uniform Gravitational Fields
 Very close to an object the
gravitational field can be
considered to be uniform.
 g has a constant value
 Further away the gravitational field
becomes weaker.
 g decreases with distance.

10. Gravitational Potential Energy
 Close to Earth, where g is constant, we know
that the energy gained by an object when it is
lifted equals the work done on it.
 EG = Work Done = Force x Distance
EG = WΔh = mgΔh
 How much GPE is gained when a 65kg object
is raised through 7.0m close to the Earth's
surface?

11. Gravitational Potential Energy
 Normally, the Earth's surface is defined
to have a GPE of 0J.
 In space, a new zero must be defined
which is the same for everyone.
 A point an infinite distance from Earth is
defined as having zero GPE.
 “Gravitational Potential Energy is a
measure of the work done to move an
object from infinity to a point within the
gravitational field”

12. Gravitational Potential Energy
 If a point an infinite distance from
Earth has zero GPE AND lifting an
object away from the Earth
increases its GPE then GPE MUST
ALWAYS BE NEGATIVE!!
 i.e. lifting an object makes its GPE
less negative!

13. Gravitational Potential Energy
 GPE is given by the formula:
EG=−G Mm
R
 Where G is the Universal Gravitational Constant
=6.67x10-11 m3kg-1s-2
 What do the other symbols mean?

14. Gravitational Potential Energy
 Calculate the GPE of a 200kg
satellite when in low Earth orbit
125km above the Earth's surface.
 What is the GPE of a 400kg
satellite in a geostationary orbit
36,000km above the Earth's
surface?
 mEarth=5.98x1024 kg
 rEarth=6.38x106 m

15. Gravitational Field Strength
 Equating our universal equation for GPE
and our close to Earth equation gives on
the Earth's surface (radius R):
mg h= G Mm
r
D -
mg R = G Mm
( )
- -
g = G M
2
0
R
R
-
 The acceleration due to gravity is not
constant! It falls off with r2.
 Notice that g is a vector and that the –
sign indicates attraction.

16. Gravitational Field Strength

17. Gravitational Field Strength
 Visit www.nineplanets.org
 Record values for the mass and
diameter of each of the 8 major
planets.
 Create a table or use a
spreadsheet to calculate values of
g for each planet.
 g=6.67E-11*mass/(radius^2)

18. Homework
 Read pages 3-4 of Keep It Simple
Science
 Complete worksheet on page 5.