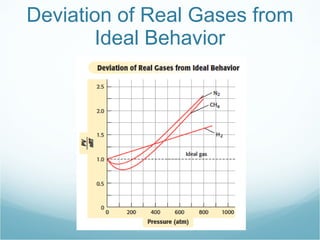
Avogadro's law states that equal volumes of gases at the same temperature and pressure contain the same number of molecules. The ideal gas law combines Boyle's, Charles', Gay-Lussac's and Avogadro's gas laws into one equation, PV=nRT, which relates the pressure (P), volume (V), number of moles (n), temperature (T) of an ideal gas. The ideal gas law accurately describes gas behavior at normal room temperature and pressure but real gases deviate from ideal behavior at high pressures due to intermolecular forces or at low temperatures where particle volume is significant.

12. Deviation of Real Gases from Ideal Behavior