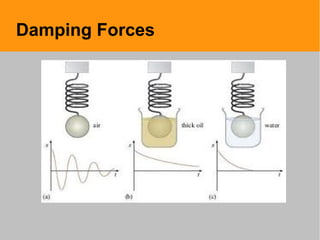
This document discusses damped and forced harmonic motion. It explains that in damped harmonic motion, a damping force acts opposite to the velocity to dissipate energy and stop vibrations. The damping causes the amplitude to decay exponentially over time. A system can be under-damped, over-damped, or critically damped depending on how quickly it stops oscillating. Forced harmonic motion occurs when an external periodic force drives the system, like pushing a swing. At resonance, the driving frequency matches the natural frequency, causing large amplitude oscillations. While resonance can be dangerous if it causes collapse, it can also be useful in applications like radios and musical instruments.

1. Topic 4 – Oscillations and Waves
4.2 Damped and Forced Harmonic Motion

2. Damped
● In SHM there is only the one restoring force
acting in the line of the displacement.
● In damped harmonic motion (DHM) an
additional damping force acts in the opposite
direction to the velocity of the object to
dissipate energy and stop the vibrations.

3. Damping Forces
● The damping force acts so as to cause the amplitude of the
vibrations to decay naturally dissipating energy.
● The general equation of this decay is A=A0
e-ˠt
● Here ˠ is a damping factor.
● The system can be under-damped
● This means the system can make more than one full oscillation
before it comes to a stop.
● The system can be over-damped
● The system comes to a stop before it completes one oscillation
● The system can be critically-damped
● The system completes exactly one oscillation before stopping.

4. Damping Forces

5. Damping Forces (beyond Syllabus)
● The general equations governing the motion of
a damped harmonic oscillation are:
x=x0 e
−γ t
cos(ωt+ ϕ)
v=−x0(γ e
−γ t
cos(ωt+ ϕ)+ ωe
−γ t
sin(ωt+ ϕ))
a=−x0 (−γ2
e−γ t
cos(ωt+ ϕ)+ ω2
e− γt
cos(ωt+ ϕ))

6. Natural Frequency
● The frequency with which a system oscillates if
it is started and allowed to move freely is called
its natural frequency.
● Simple harmonic motion occurs at the natural
frequency.
● Often, extra energy is imparted into the system
each oscillation by another external periodic
force.
● This is like a child pushing a swing to keep it going.
● Such a system is said to be a forced harmonic
oscillator.

7. Forced Harmonic Motion
● The equation for forced harmonic motion (with
some damping) would be:
● Here the first part of the equation is the normal
SHM equation with natural frequency ω0
and
amplitude x0
● The second part of the equation is due to the
forcing (driving) force of magnitude F and
driving frequency ω
x=x0e
− γt
cos(ω0t)+
F
mω
2
cos(ωt)

8. Forced Harmonic Motion and Resonance
● As the driving frequency of the system
approaches the natural frequency of the
system, the amplitude of the system increases
dramatically.
● The force adds energy to each swing making
the amplitude continue to increase and
increase.
● When the two frequencies are identical, then
the system is said to be at resonance.

9. Resonance
● The state in which the frequency of the
externally applied periodic force equals the
natural frequency of the system is called
resonance.
● This causes oscillations with large amplitudes.
● Damping causes the maximum amplitude to be
limited.

10. Resonance
-5 0
1 9 5 0
3 9 5 0
5 9 5 0
7 9 5 0
9 9 5 0
1 1 9 5 0
1 3 9 5 0
0 5 1 0 1 5 2 0 2 5 3 0 3 5 4 0 4 5 5 0
MaximumAmplitude
D r iv in g F r e q u e n c y
V e r y L ig h t d a m p in g
L ig h t d a m p in g
M e d iu m D a m p in g
H e a v y D a m p in g

11. Dangerous Resonance
● Resonance can be
disastrous
● If a bridge happens to
have a natural frequency
that is in the range of the
frequencies that can be
generated by the wind
then the bridge can
oscillate.
● The bridge can then
vibrate it can collapse!
● This is resonance at its
worst!!!

12. Useful Resonance
● Resonance can be useful.
● A radio is tuned by causing a quartz crystal to
resonate at a particular frequency.
● Wind instruments rely on the resonance of a
vibrating air column to make an audible sound.
– Because of the sharp spike on the frequency response
curve, other frequencies are cancelled out and not heard.