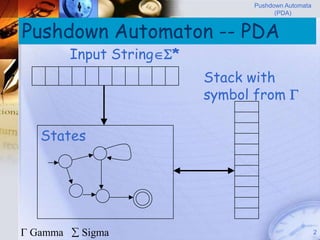
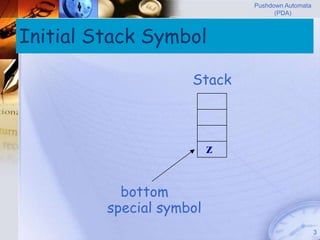
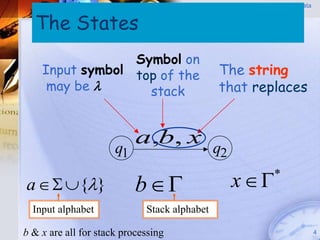
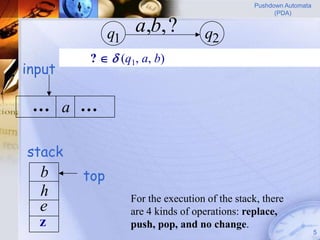
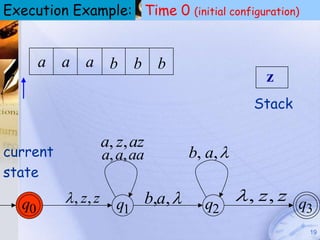
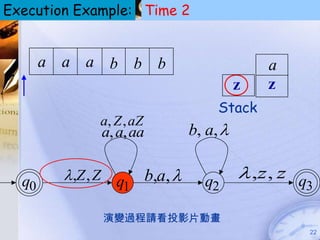
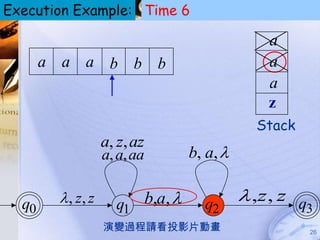
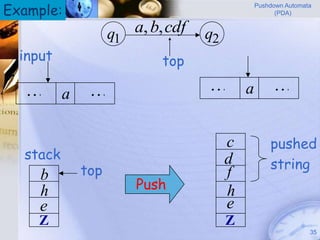
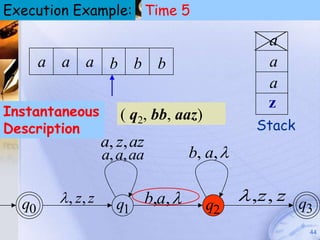
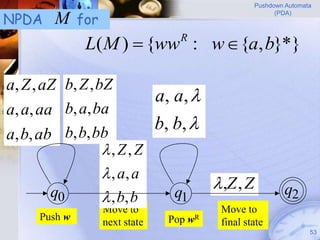
Pushdown automata (PDA) are machines that process input strings and use a stack to determine transitions between states. A PDA consists of states, input symbols, stack symbols, transition functions, an initial state, initial stack symbol, and final states. The transition function specifies how the PDA moves between states based on the current state, input symbol, and top stack symbol, and may involve operations like replacing, pushing, or popping symbols from the stack. PDAs can recognize languages like {anbn: n ≥ 0} by pushing a symbol for each a and popping for each b.

1. Pushdown Automata
(PDA)
Pushdown Automata
PDAs
Homework (p.183) 2, 3abc, 4a~h, 5, 6, 9~11
1

2. Pushdown Automata
(PDA)
Pushdown Automaton -- PDA
Input String*
Stack with
symbol from 
States
 Gamma  Sigma 2

3. Pushdown Automata
(PDA)
Initial Stack Symbol
Stack
z
bottom
special symbol
3

4. Pushdown Automata
The States
(PDA)
Symbol on
Input symbol top of the The string
may be  stack that replaces
q1
a,b, x q
2
a   {} b x *
Input alphabet Stack alphabet
b & x are all for stack processing 4

5. Pushdown Automata
(PDA)
q1 a,b, ? q2
?   (q1, a, b)
input
… a …
stack
b top
h For the execution of the stack, there
e are 4 kinds of operations: replace,
z push, pop, and no change.
5

6. Pushdown Automata
(PDA)
q1 a,b, ? q2
(q2, c)   (q1, a, b): when it is on the state q1 and
input a is read, then b is replace by c and moves to q2
… a … … a …
stack
b top c
h Replace h
e e
z z 6

7. Pushdown Automata
(PDA)
q1 a,b, c q2
(q2, c)   (q1, a, b): when it is on the state q1 and
input a is read, then b is replace by c and moves to q2
… a … … a …
stack
b top c
h Replace h
e e
z z 7

8. Pushdown Automata
(PDA)
q1 a,b, ? q2
(q2, cb)   (q1, a, b): when it is on the state q1 and a is read,
input
then c is pushed, i.e. b is replace by cb, and moves to q2
… a … … a …
stack c
b top b
h Push h
e e
z In Def 7.1 (p.177), it is written as (q2, cb)  (q1, a, b)
for pushing.
z
For the execution of the stack, there are 4 kinds of
operations: replace, push, pop, and no change.
8

9. Pushdown Automata
(PDA)
q1 a,b, cb q2
(q2, cb)   (q1, a, b): when it is on the state q1 and a is read,
input
then c is pushed, i.e. b is replace by cb, and moves to q2
… a … … a …
stack c
b top b
h Push h
e e
z z
9

10. Pushdown Automata
(PDA)
q1 a,b, ? q2
(q2, )   (q1, a, b): when it is on the state q1 and a is read,
input
then b is popped, i.e. b is replace by , and moves to q2
… a … … a …
stack
b top Pop h
h e
e Beware, when we push a symbol into stack—we do z
not really care about what is the top symbol of the
z stack.
But if we want to pop a symbol out of a stack, we
need to know what is the top stack symbol (will be
popped up). 10

11. Pushdown Automata
a,b, 
(PDA)
q1 q2
(q2, )   (q1, a, b): when it is on the state q1 and a is read,
input
then b is popped, i.e. b is replace by , and moves to q2
… a … … a …
stack
b top
h Pop h
e e
z z 11

12. Pushdown Automata
(PDA)
q1 a,b, ? q2
(q2, b)   (q1, a, b): when it is on the state q1 and a is read,
input
nothing will be changed on the stack and moves to q2
… a … … a …
stack
b top b
h No Change h
e e
z z
12

13. Pushdown Automata
(PDA)
q1 a,b, b q2
(q2, b)   (q1, a, b): when it is on the state q1 and a is read,
input
nothing will be changed on the stack and moves to q2
… a … … a …
stack
b top b
h No Change h
e e
z z
13

14. Pushdown Automata
(PDA)
Every FA is a PDA
Consider regular language L={ a2nbm : n, m  0}
with FA as:
b , z, z
a , z, z
a , z, z
 , z, z
It becomes a PDA !
14

15. Pushdown Automata
Every FA is a PDA
(PDA)
LM   L(a * b)
a, z, z
a , z, z a b
b,,z, z
a, z, z
b, z, z b, , b z
a z,
q0 q1 q2
It becomes a PDA !
Do Hw#3 on p. 183
15

16. Pushdown Automata
(PDA)
While it is on state q1 and reads a Non-Determinism
If top of stack symbol is b: (q2, c)   (q1, a, b)
q2   transition
a,b, c
q1  ,b, c q2
q1 If top of stack symbol is b: moves to q2 without
consuming any input symbol, i.e. (q2,c) (q1,, b)
a,d , ed
q3
If top of stack symbol is d: (q3, ed)   (q1, a, d)
These are allowed transitions in
a Non-deterministic PDA (NPDA) 16

17. Formal Definition
Pushdown Automata
(PDA)
Non-Deterministic Pushdown Automaton
NPDA
M  (Q, Σ, Γ, δ, q0 , z, F ) Final
States states
Input Stack
alphabet Transition Initial start
Stack
function state symbol
alphabet
17

18. NPDA: Non-Deterministic
Pushdown Automata
(PDA)
PDA
Example:
a, z, az
a, a, aa b, a, 
q0  , z, z q1 b,a,  q2
 , z, z q
3
According to the def. 7.1, , should be
replaced by ,$$
transitions on q1 should be { a,$a$, a, aaa}
18

19. Execution Example: Time 0 (initial configuration)
Pushdown Automata
(PDA)
a a a b b b
z
Stack
a, z, az
current a, a, aa b, a, 
state
q0  , z, z q1 b,a,  q2
 , z, z q
3
19

20. Execution Example: Time 1
Pushdown Automata
(PDA)
a a a b b b
z
Stack
a, z, az
a, a, aa b, a, 
q0  , z, z q1 b,a,  q  ,z, z q
2 3
20

21. Execution Example: Time 1
Pushdown Automata
(PDA)
a a a b b b
z
Stack
a, z, az
a, a, aa b, a, 
q0  , z, z q1 b,a,  q2
 ,z, z q
3
21

22. Execution Example: Time 2
Pushdown Automata
(PDA)
a a a b b b a
z z
Stack
a, Z , aZ
a, a, aa b, a, 
q0  ,Z, Z q b,a,  q2
 ,z, z q
1 3
演變過程請看投影片動畫
22

23. Execution Example: Time 3
Pushdown Automata
(PDA)
a
a a a b b b a a
z z
Stack
a, Z , aZ
a, a, aa b, a, 
q0  , z, z q1 b,a,  q2
 ,z, z q
3
演變過程請看投影片動畫 23

24. Execution Example: Time 4
Pushdown Automata
(PDA)
a
a a a b b b a a
a a
z z
Stack
a, z, az
a, a, aa b, a, 
q0  , z, z q1 b,a,  q2
 ,z, z q
3
演變過程請看投影片動畫 24

25. Execution Example: Time 5
Pushdown Automata
(PDA)
a
a a a b b b a
a
z
Stack
a, z, az
a, a, aa b, a, 
q0  , z, z q1 b,a,  q2
 ,z, z q
3
演變過程請看投影片動畫 25

26. Execution Example: Time 6
Pushdown Automata
(PDA)
a
a a a b b b a
a
z
Stack
a, z, az
a, a, aa b, a, 
q0  , z, z q1 b,a,  q2
 ,z, z q
3
演變過程請看投影片動畫 26

27. Execution Example: Time 7
Pushdown Automata
(PDA)
a
a a a b b b a
a
z
Stack
a, z, az
a, a, aa b, a, 
q0  , z, z q1 b,a,  q2
 ,z, z q
3
演變過程請看投影片動畫 27

28. Execution Example: Time 8
Pushdown Automata
(PDA)
a
a a a b b b a
a
z
Stack
a, z, az
a, a, aa b, a, 
q0  , z, z q1 b,a,  q2
 ,z, z q
3
演變過程請看投影片動畫 28

29. Execution Example: End of input tape
Pushdown Automata
(PDA)
a
a a a b b b a
a
z
Stack
a, z, az
a, a, aa b, a, 
accept
q0  , z, z q1 b,a,  q2
 ,z, z q
3
演變過程請看投影片動畫 29

30. Pushdown Automata
(PDA)
A string is accepted if there is
a computation such that:
• All the input is consumed
and
• The last state is a final state
At the end of the computation,
we do not care about the stack contents
30

31. Pushdown Automata
(PDA)
Therefore:
The input string aaabbb
is accepted by the NPDA:
a, z, az
a, a, aa b, a, 
q0  , z, z q1 b,a,  q2
 , z, z q
3
31

32. Pushdown Automata
(PDA)
L( M ) = ? { anbn : n  0 }
is the language accepted by the NPDA:
a, z, az
a, a, aa b, a, 
q0  , z, z q1 b,a,  q2
 , z, z q
3
32

33. Pushdown Automata
(PDA)
L( M ) = { anbn : n  0 }
Can we find a machine with 3 states?
Can we find a machine with 2 states?
What is L(M) if both q0 & q1 are final states?
a, z, az
a, a, aa b, a, 
q0  , z, z q1 b,a,  q2
 , z, z q
3
33

34. Pushdown Automata
(PDA)
Pushing Strings
Input Top stack Push
symbol symbol string
q1
a, b, w q2
The top stack symbol b is
replaced by the string w
34

35. Example:
Pushdown Automata
(PDA)
q1 a, b, cdf q2
input top

 a 
 
 a 

c pushed
stack d
top string
b f
h Push h
e e
Z Z
35

36. Example:
Pushdown Automata
(PDA)
input
Beware: we can push a string into a stack
but we do not pop a string from a stack---
only a 
  
 pop one symbol or nothing at a a 
 time! 
c pushed
stack d
top string
b f
h Push h
e e
Z Z
In fact, to read from input tape or pop up from stack, there is at most one symbol at
a time. The main reason is we can only see one symbol at a time.
As to push into stack is like to record an information so we can write a string, or
push a string into a stack. 36

37. Pushdown Automata
Examples for NPDA
(PDA)
Construct an NPDA for
LM   {a b
n 2n
: n  0}
LM   {a b : n  0}
2n n
LM   {a b c
n m nm
: n, m  0}
37

38. Formal Def. for NPDA M
Pushdown Automata
(PDA)
L ={ anbn : n  0 }
M  ({q0 , q1 , q2 , q3},   {a, b},   {a, b, z},
 , q0 , z, F  {q0 , q3})
a, z, az
a, a, aa b, a, 
q0  , z, z q1 b,a,  q2
 , z, z q
3
38

39. Pushdown Automata
Transition function: (PDA)
q2
a, b, w
q1
a, b, w
q3
 (q1, a, b)  {(q2 , w), (q3 , w)}
 : Q  ({}  )    finite subsets of Q   *
39

40. M  ({q0 , q1 , q2 , q3},   {a, b},   {a, b, z},
Pushdown Automata
(PDA)
 , q0 , z, F  {q0 , q3})
Transition Functions  ?
a, z, az
a, a, aa b, a, 
q0  , z, z q1 b,a,  q2
 , z, z q
3
40

41. Pushdown Automata
(PDA)
Transition Functions 
(q1, a, z) = {(q1, az)}
(q1, a, a) = {(q1, aa)} (q2, b, a) = {(q2, )}
a, z, az
a, a, aa b, a, 
q0  , z, z q1 b,a,  q2
 , z, z q
3
(q0, , z) = {(q1, z)} (q1, b, a) = {(q2, )} (q2, , z) = {(q3, z)}
41

42. Pushdown Automata
(PDA)
Instantaneous Description
( q, u , s )
Current Current
Remaining
state stack
input
contents
42

43. Pushdown Automata
(PDA)
Time 4
a
a a a b b b a
a
z
Instantaneous ( q1, bbb, aaaz)
Description Stack
a, z, az
a, a, aa b, a, 
q0  , z, z q1 b,a,  q2
 ,z, z q
3
43

44. Execution Example: Time 5
Pushdown Automata
(PDA)
a
a a a b b b a
a
z
Instantaneous ( q2, bb, aaz)
Description Stack
a, z, az
a, a, aa b, a, 
q0  , z, z q1 b,a,  q2
 ,z, z q
3
44

45. Pushdown Automata
(PDA)
We write:
(q1 , bbb, aaaZ ) ├ (q2 , bb, aaZ )
Time 4 Time 5
45

46. Pushdown Automata
(PDA)
A computation for w= aaabbb:
(q0 , aaabbb, z )├ (q1 , aaabbb, z ) ├
(q1 , aabbb, az)├ (q1 , abbb, aaz) ├ (q1 , bbb, aaaz) ├
(q2 , bb, aaz)├ (q2 , b, az) ├ (q2 ,  , z ) ├(q3 ,  , z )
a, z, az
a, a, aa b, a, 
q0  , z, z q1 b,a,  q2
 , z, z q
3
46

47. Pushdown Automata
(PDA)
(q0 , aaabbb, z ) (q1 , aaabbb, z )├
├
(q1 , aabbb, az)├ (q1 , abbb, aaz) ├ (q1 , bbb, aaaz) ├
(q2 , bb, aaz) (q2 , b, az)├ (q2 ,  , z )├ (q3 ,  , z )
├
For convenience we write:
(q0 , aaabbb, z ) ├ (q3 ,  , z )
*
47

48. Pushdown Automata
(PDA)
Formal Definition
Language of NPDA M :
*

L( M )  {w : (q0 , w, z )├ (q f ,  , u )}
Initial state Final state empty
48

49. Example:
Pushdown Automata
(PDA)

(q0 , aaabbb, z ) ├ (q3 ,  , z )
aaabbb L(M )
NPDA M :
a, z, az
a, a, aa b, a, 
q0  , z, z q1 b,a,  q2
 , z, z q
3
49

50. Pushdown Automata
(PDA)

(q0 , a b , z ) ├ (q3 ,  , z )
n n
a b  L(M )
n n
NPDA M :
a, z, az
a, a, aa b, a, 
q0  , z, z q1 b,a,  q2
 , z, z q
3
50

51. Pushdown Automata
(PDA)
Therefore: L( M )  {a b : n  0}
n n
NPDA M :
a, z, az
a, a, aa b, a, 
q0  , z, z q1 b,a,  q2
 , z, z q
3
51

52. Pushdown Automata
(PDA)
Another NPDA example
NPDA M for
L( M )  {ww : w {a, b}*}
R
52

53. Pushdown Automata
NPDA M for (PDA)
L( M )  {ww : w {a, b}*}
R
a, Z , aZ b, Z , bZ
a, a, 
a, a, aa b, a, ba
b, b, 
a, b, ab b, b, bb
, Z , Z
 , a, a
 ,Z, Z q2
q0  , b, b q1
Move to Move to
Push w next state Pop wR final state
53

54. NPDA M for L( M )  {ww : w  {a, b}*}
R Pushdown Automata
(PDA)
Try strings like: , abba, baa.
If it is accepted, write the computation.
a , z , az b, z , bz
a , a , aa b, a, ba a, a, 
a , b, ab b, b, bb b, b, 
 , z, z
 , a, a  ,z, z
q0 q1 q2
 , b, b 54

55. NPDA M for L( M )  {ww : w  {a, b}*}
R Pushdown Automata
(PDA)
M  ({q0 , q1 , q2 },   {a, b},   {a, b, z},
 , q0 , z, F  {q2 })
How about for L( M )  {wcw : w  {a, b}*}
R
a , z , az b, z , bz
a , a , aa b, a, ba a, a, 
a , b, ab b, b, bb b, b, 
 , z, z
 , a, a  ,z, z
q0 q1 q2
 , b, b 55

56. Pushdown Automata
(PDA)
Another NPDA example
NPDA M for
L( M )  {w : na  nb }
How to use the stack to recognize
the strings like :
abbbaa babbaaba 
56

57. M for L( M )  {w : na  nb }
Pushdown Automata
NPDA (PDA)
M  ({q1 , q2},   {a, b},   {0,1, z},  , q1 , Z , F  {q2})
Write a computation for abbbaa.
a,z,0 z b,z,1z
a,0,00 b,1,11
a,1,  b,0, 
q1
 , z, z q2
57

58. M for L( M )  {w : na  nb }
Pushdown Automata
NPDA (PDA)
How about NPDA for {w: na = nb+1 } ?
How about NPDA for {w: na = 2nb } ?
a,z,0 z b,z,1z
a,0,00 b,1,11
a,1,  b,0, 
q1
 , z, z q2
{w: na = 2nb }: one b and push 2 bs, or push one b and pop up one a, or pop up two
as, i.e., b, z, bbz; b, b, bbb in q1, but b, a, (pop up and go to another state, say q’,
such that ,a,  (pop up one more time); or , z, bz; or , b, bb; and all go back to
state q1.
58

59. M for L( M )  {w : na  2nb }
Pushdown Automata
NPDA (PDA)
a,Z ,0Z b,Z ,1Z b,Z ,11Z
a,0,00 b,1,11 b,1,111
a,1,  b,0, 
q3
 ,Z ,1Z
 ,0, 
q1 q2
 , Z, Z
59

60. Pushdown Automata
More Example on designing:
(PDA)
LM   {a b : n  m  2n}
n m
How about NPDA for {anbm: n < m } ?
How about NPDA for {anbm: n > m } ?
How about NPDA for {anbm: n  m } ?
60