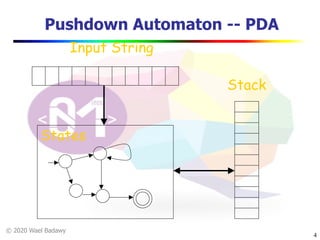
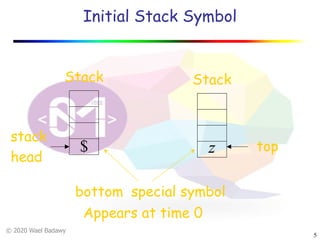
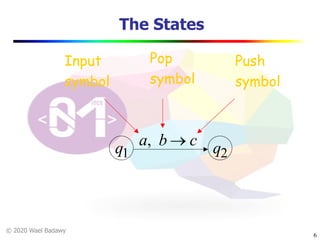
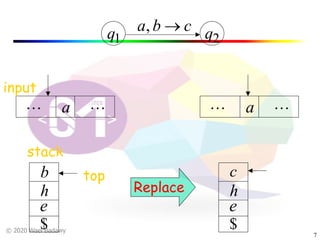
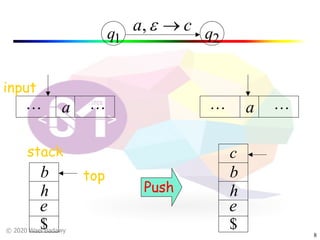
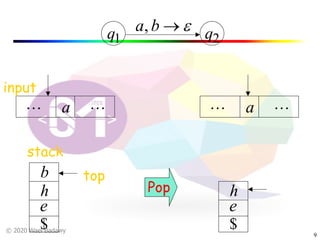
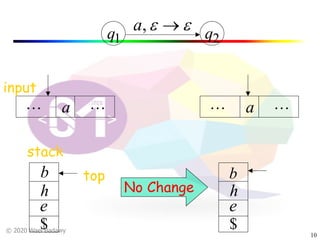
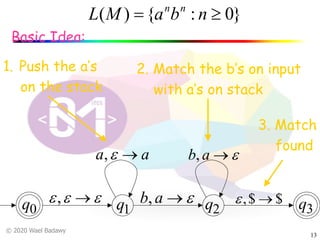
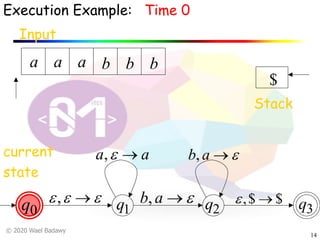
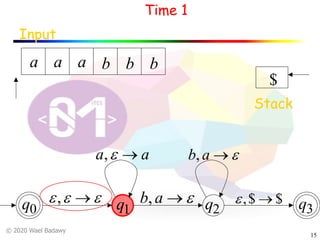
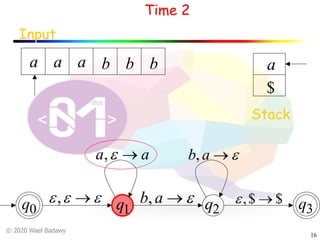
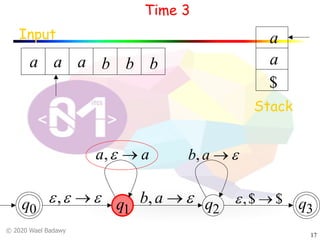
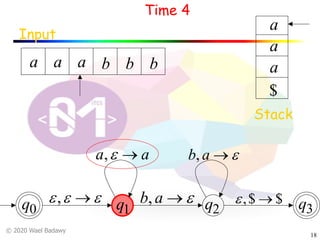
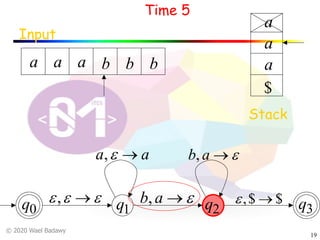
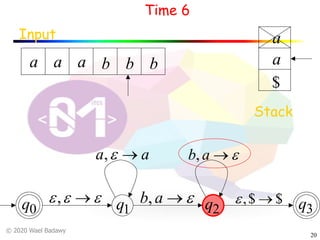
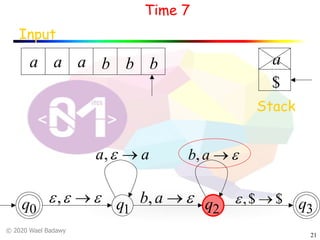
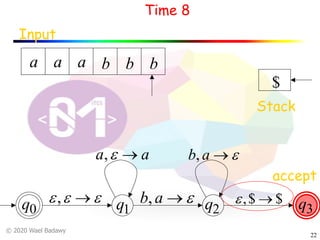
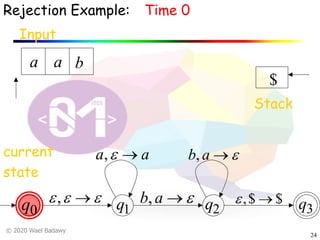
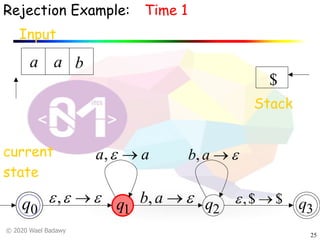
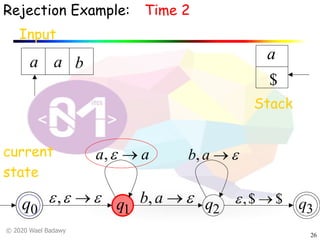
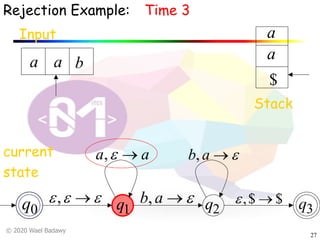
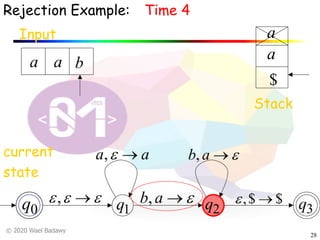
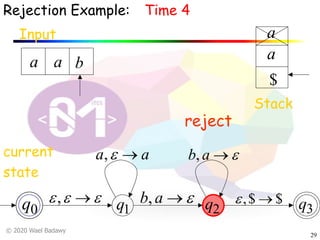
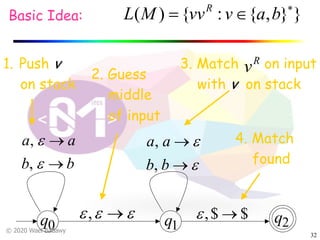
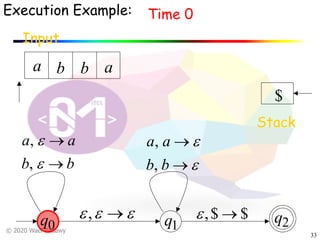
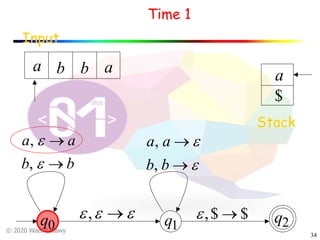
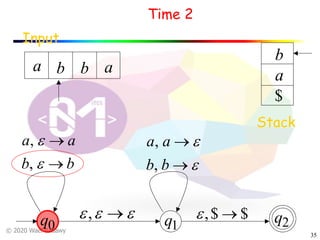
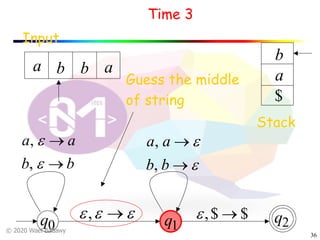
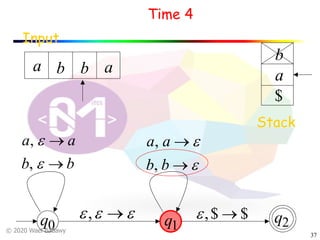
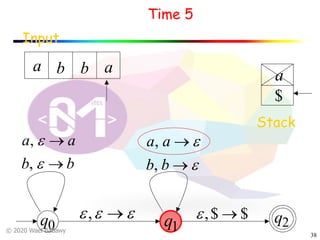
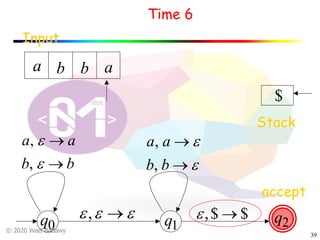
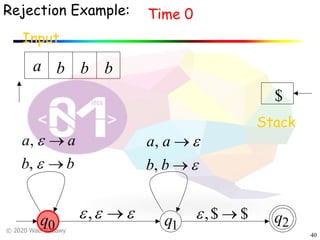
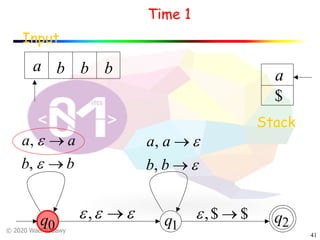
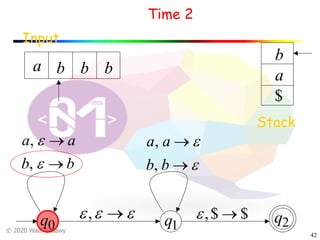
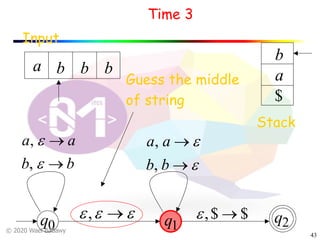
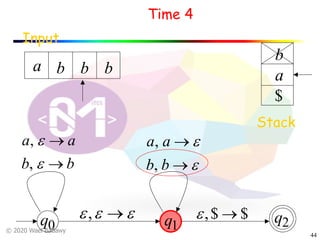
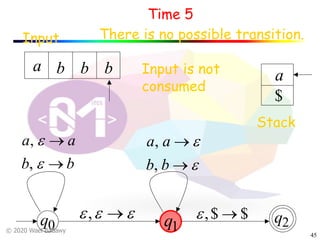
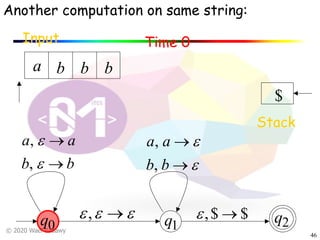
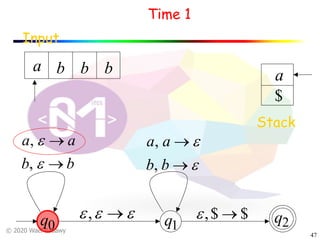
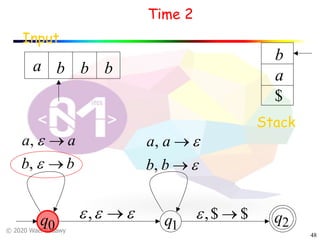
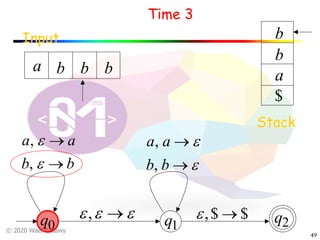
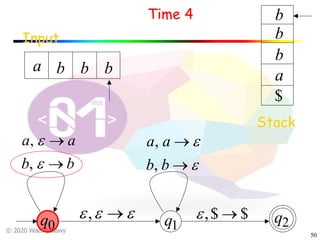
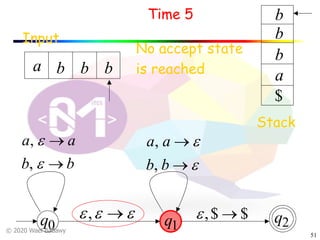
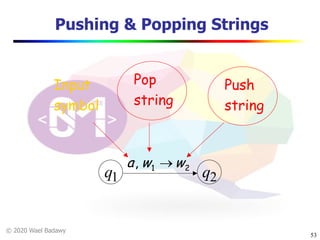
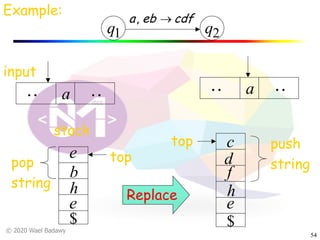
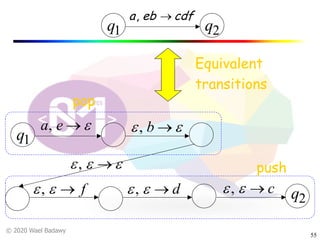
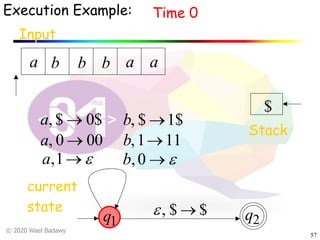
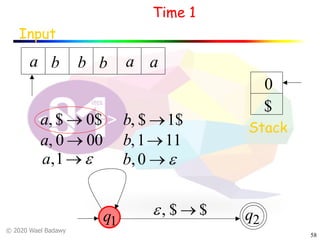
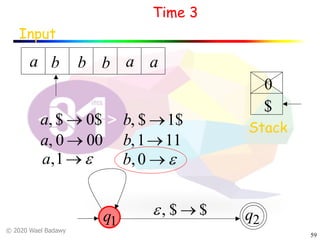
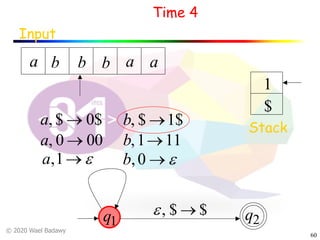
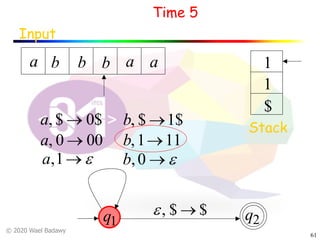
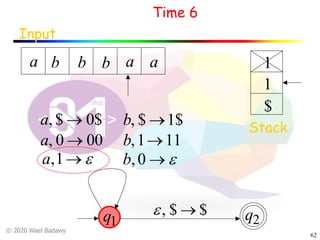
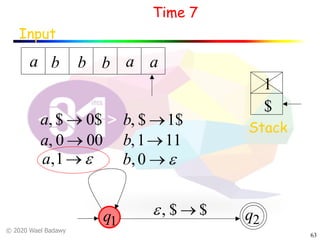
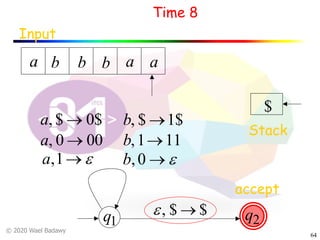
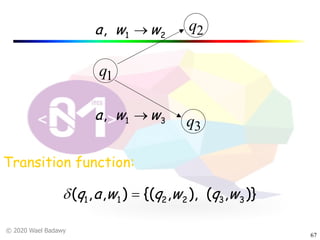
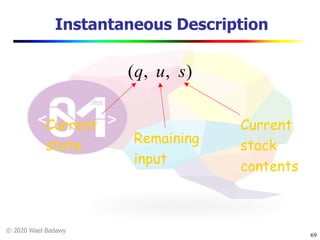
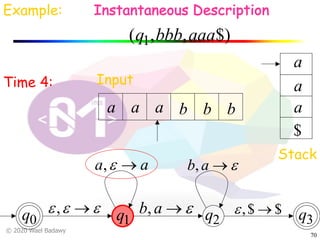
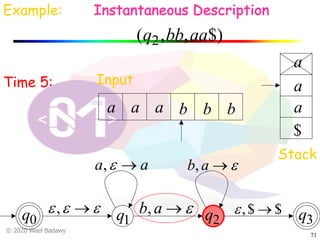
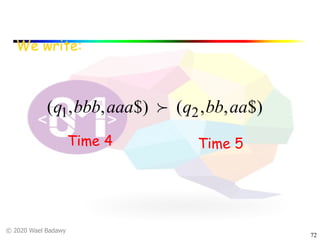
The document discusses pushdown automata (PDAs). It begins with an overview of the components of a PDA - the input string, stack, states, and transitions. It then provides examples of PDA configurations and computations for accepting and rejecting strings. Key points made include: PDAs are non-deterministic, a string is accepted if the entire input is consumed in an accepting state, and strings can be pushed and popped from the stack individually or as strings. The document uses several examples to demonstrate how PDAs work.

1. © 2020 Wael Badawy
1
Pushdown Automata
PDAs
1
DISCLAIMER:
This video is optimized for HD large display using
patented and patent-pending “Nile Codec”, the first
Egyptian Video Codec for more information,
PLEASE check https://NileCodec.com
Also available as a PodCast

2. © 2020 Wael Badawy
Copyright © 2020 Wael Badawy. All rights reserved
n This video is subject to copyright owned by Wael Badawy “WB”. Any
reproduction or republication of all or part of this video is expressly prohibited
unless WB has explicitly granted its prior written consent. All other rights
reserved.
n This video is intended for education and information only and is offered AS IS,
without any warranty of the accuracy or the quality of the content. Any other
use is strictly prohibited. The viewer is fully responsible to verify the accuracy
of the contents received without any claims of costs or liability arising .
n The names, trademarks service marked as logos of WB or the sponsors
appearing in this video may not be used in any any product or service,
without prior express written permission from WB and the video sponsors
n Neither WB nor any party involved in creating, producing or delivering
information and material via this video shall be liable for any direction,
incidental, consequential, indirect of punitive damages arising out of access
to, use or inability to use this content or any errors or omissions in the
content thereof.
n If you will continue to watch this video, you agree to the terms above and
other terms that may be available on http://nu.edu.eg & https://caiwave.net
2

3. © 2020 Wael Badawy

4. © 2020 Wael Badawy
Pushdown Automaton -- PDA
4
Input String
Stack
States

5. © 2020 Wael Badawy
5
Initial Stack Symbol
Stack
$
Stack
z
bottom special symbol
stack
head
top
Appears at time 0

6. © 2020 Wael Badawy
The States
6
q1 q2
a, b ® c
Input
symbol
Pop
symbol
Push
symbol

7. © 2020 Wael Badawy
7
q1 q2
cba ®,
a! !
b top
input
stack
a! !
Replace
e
h
$
e
h
$
c

8. © 2020 Wael Badawy
8
q1 q2
ca ®e,
a! ! a! !
Push
b
e
h
$
e
h
$
b
c
top
input
stack

9. © 2020 Wael Badawy
9
q1 q2
e®ba,
a! ! a! !
Pop
b
e
h
$
e
h
$
top
input
stack

10. © 2020 Wael Badawy
10
q1 q2
ee ®,a
a! ! a! !
No Change
b
e
h
$
e
h
$
btop
input
stack

11. © 2020 Wael Badawy
Non-Determinism
11
q1
q2a, b ® c
q3
a, b ® c
q1 q2
cb ®,e
transition-e
PDAs are non-deterministic
Allowed non-deterministic transitions

12. © 2020 Wael Badawy
Example PDA
}0:{)( ³= nbaML nn
12
eee ®,
aa ®e,
e®ab,q0 q1 q2 q3
e®ab,
$$, ®e
PDA :M

13. © 2020 Wael Badawy
}0:{)( ³= nbaML nn
13
q0 q1 q2 q3
Basic Idea:
1. Push the a’s
on the stack
2. Match the b’s on input
with a’s on stack
3. Match
found
eee ®,
aa ®e,
e®ab,
e®ab,
$$, ®e

14. © 2020 Wael Badawy
14
0q q1 q2 q3
Execution Example:
Input
a a a b b b
current
state
Time 0
Stack
$
eee ®,
aa ®e,
e®ab,
e®ab,
$$, ®e

15. © 2020 Wael Badawy
15
q0 q1 q2 q3
Input
a a a b b b
Time 1
Stack
$
eee ®,
aa ®e,
e®ab,
e®ab,
$$, ®e

16. © 2020 Wael Badawy
16
q0 q1 q2 q3
Input
Stack
a a a b b b
$
a
Time 2
eee ®,
aa ®e,
e®ab,
e®ab,
$$, ®e

17. © 2020 Wael Badawy
17
q0 q1 q2 q3
Input
Stack
a a a b b b
$
a
a
Time 3
eee ®,
aa ®e,
e®ab,
e®ab,
$$, ®e

18. © 2020 Wael Badawy
18
q0 q1 q2 q3
Input
Stack
a a a b b b
$
a
a
a
Time 4
eee ®,
aa ®e,
e®ab,
e®ab,
$$, ®e

19. © 2020 Wael Badawy
19
q0 q1 q2 q3
Input
a a a b b b
Stack
$
a
a
a
Time 5
eee ®,
aa ®e,
e®ab,
e®ab,
$$, ®e

20. © 2020 Wael Badawy
20
q0 q1 q2 q3
Input
a a a b b b
$
a
Stack
Time 6
a
eee ®,
aa ®e,
e®ab,
e®ab,
$$, ®e

21. © 2020 Wael Badawy
21
q0 q1 q2 q3
Input
a a a b b b
$
Stack
Time 7
a
eee ®,
aa ®e,
e®ab,
e®ab,
$$, ®e

22. © 2020 Wael Badawy
22
q0 q1 q2 q3
Input
a a a b b b
Time 8
accept
$
Stack
eee ®,
aa ®e,
e®ab,
e®ab,
$$, ®e

23. © 2020 Wael Badawy
23
A string is accepted if there is
a computation such that:
All the input is consumed
AND
The last state is an accepting state
we do not care about the stack contents
at the end of the accepting computation

24. © 2020 Wael Badawy
24
0q q1 q2 q3
Rejection Example:
Input
a a b
current
state
Time 0
Stack
$
eee ®,
aa ®e,
e®ab,
e®ab,
$$, ®e

25. © 2020 Wael Badawy
25
0q q1 q2 q3
Rejection Example:
Input
a a b
current
state
Time 1
Stack
$
eee ®,
aa ®e,
e®ab,
e®ab,
$$, ®e

26. © 2020 Wael Badawy
26
0q q1 q2 q3
Rejection Example:
Input
a a b
current
state
Time 2
Stack
$
a
eee ®,
aa ®e,
e®ab,
e®ab,
$$, ®e

27. © 2020 Wael Badawy
27
0q q1 q2 q3
Rejection Example:
Input
a a b
current
state
Time 3
Stack
$
a
a
eee ®,
aa ®e,
e®ab,
e®ab,
$$, ®e

28. © 2020 Wael Badawy
28
0q q1 q2 q3
Rejection Example:
Input
a a b
current
state
Time 4
Stack
$
a
a
eee ®,
aa ®e,
e®ab,
e®ab,
$$, ®e

29. © 2020 Wael Badawy
29
0q q1 q2 q3
Rejection Example:
Input
a a b
current
state
Time 4
Stack
$
a
a
reject
eee ®,
aa ®e,
e®ab,
e®ab,
$$, ®e

30. © 2020 Wael Badawy
30
The string is rejected by the PDAaab
q0 q1 q2 q3
There is no accepting computation for aab
eee ®,
aa ®e,
e®ab,
e®ab,
$$, ®e

31. © 2020 Wael Badawy
Another PDA example
31
$$, ®eq1
q2
bb
aa
®
®
e
e
,
,
eee ®,q0
e
e
®
®
bb
aa
,
,
PDA :M }},{:{)( *
Î= bavvvML R

32. © 2020 Wael Badawy
R
v
32
q1
q2q0
}},{:{)( *
Î= bavvvML R
Basic Idea:
1. Push v
on stack
2. Guess
middle
of input
3. Match on input
with v on stack
4. Match
found
$$, ®e
bb
aa
®
®
e
e
,
,
eee ®,
e
e
®
®
bb
aa
,
,

33. © 2020 Wael Badawy
33
Execution Example:
Input
Time 0
Stack
$
q1
q2q0
a ab b
$$, ®e
bb
aa
®
®
e
e
,
,
eee ®,
e
e
®
®
bb
aa
,
,

34. © 2020 Wael Badawy
34
Input
a ab
Time 1
Stack
$
q1
q2q0
ab
$$, ®e
bb
aa
®
®
e
e
,
,
eee ®,
e
e
®
®
bb
aa
,
,

35. © 2020 Wael Badawy
35
Input
Time 2
Stack
$
q1
q2q0
a
a ab b
b
$$, ®e
bb
aa
®
®
e
e
,
,
eee ®,
e
e
®
®
bb
aa
,
,

36. © 2020 Wael Badawy
36
Input
Time 3
Stack
$
q1
q2q0
a
a ab b
b
Guess the middle
of string
$$, ®e
bb
aa
®
®
e
e
,
,
eee ®,
e
e
®
®
bb
aa
,
,

37. © 2020 Wael Badawy
37
Input
Time 4
Stack
$
q1
q2q0
a
a ab b
b
$$, ®e
bb
aa
®
®
e
e
,
,
eee ®,
e
e
®
®
bb
aa
,
,

38. © 2020 Wael Badawy
38
Input
Time 5
Stack
$
1q q2q0
a ab b a
$$, ®e
bb
aa
®
®
e
e
,
,
eee ®,
e
e
®
®
bb
aa
,
,

39. © 2020 Wael Badawy
39
Input
Time 6
Stack
$
q1q0
a ab b
accept
q2
$$, ®e
bb
aa
®
®
e
e
,
,
eee ®,
e
e
®
®
bb
aa
,
,

40. © 2020 Wael Badawy
40
Rejection Example:
Input
Time 0
Stack
$
q1
q2q0
a b b b
$$, ®e
bb
aa
®
®
e
e
,
,
eee ®,
e
e
®
®
bb
aa
,
,

41. © 2020 Wael Badawy
41
Input
Time 1
Stack
$
q1
q2q0
a
a b b b
$$, ®e
bb
aa
®
®
e
e
,
,
eee ®,
e
e
®
®
bb
aa
,
,

42. © 2020 Wael Badawy
42
Input
Time 2
Stack
$
q1
q2q0
a
b
a b b b
$$, ®e
bb
aa
®
®
e
e
,
,
eee ®,
e
e
®
®
bb
aa
,
,

43. © 2020 Wael Badawy
43
Input
Time 3
Stack
$
q1
q2q0
a
b
Guess the middle
of string
a b b b
$$, ®e
bb
aa
®
®
e
e
,
,
eee ®,
e
e
®
®
bb
aa
,
,

44. © 2020 Wael Badawy
44
Input
Time 4
Stack
$
q1
q2q0
a
b
a b b b
$$, ®e
bb
aa
®
®
e
e
,
,
eee ®,
e
e
®
®
bb
aa
,
,

45. © 2020 Wael Badawy
45
Input
Time 5
Stack
$
1q q2q0
a
a b b b
There is no possible transition.
Input is not
consumed
$$, ®e
bb
aa
®
®
e
e
,
,
eee ®,
e
e
®
®
bb
aa
,
,

46. © 2020 Wael Badawy
46
Another computation on same string:
Input Time 0
Stack
$
q1
q2q0
a b b b
$$, ®e
bb
aa
®
®
e
e
,
,
eee ®,
e
e
®
®
bb
aa
,
,

47. © 2020 Wael Badawy
47
Input
Time 1
Stack
$
q1
q2q0
a
a b b b
$$, ®e
bb
aa
®
®
e
e
,
,
eee ®,
e
e
®
®
bb
aa
,
,

48. © 2020 Wael Badawy
48
Input
Time 2
Stack
$
q1
q2q0
a
b
a b b b
$$, ®e
bb
aa
®
®
e
e
,
,
eee ®,
e
e
®
®
bb
aa
,
,

49. © 2020 Wael Badawy
49
Input
Time 3
Stack
$
a
b
a b b b
q1
q2q0
b
$$, ®e
bb
aa
®
®
e
e
,
,
eee ®,
e
e
®
®
bb
aa
,
,

50. © 2020 Wael Badawy
50
Input
Time 4
Stack
a b b b
q1
q2q0
$
a
b
b
b
$$, ®e
bb
aa
®
®
e
e
,
,
eee ®,
e
e
®
®
bb
aa
,
,

51. © 2020 Wael Badawy
51
Input
Time 5
Stack
a b b b
$
a
b
b
b
q1
q2q0
No accept state
is reached
$$, ®e
bb
aa
®
®
e
e
,
,
eee ®,
e
e
®
®
bb
aa
,
,

52. © 2020 Wael Badawy
52
q1
q2q0
There is no computation
that accepts string abbb
)(MLabbbÏ
$$, ®e
bb
aa
®
®
e
e
,
,
eee ®,
e
e
®
®
bb
aa
,
,

53. © 2020 Wael Badawy
Pushing & Popping Strings
53
q1 q2
21, wwa ®
Input
symbol
Push
string
Pop
string

54. © 2020 Wael Badawy
54
q1 q2
cdfeba ®,
a!!" !!"
b
top
input
stack
a!!" !!"
Replace
e
h h
e
c
d
f
push
string
Example:
$ $
e
pop
string
top

55. © 2020 Wael Badawy
55
q1 q2
cdfeba ®,
q1
q2
e®ea, ee ®b,
f®ee,
eee ®,
d®ee, c®ee,
pop
push
Equivalent
transitions

56. © 2020 Wael Badawy
Another PDA example
56
$$, ®eq1 q2
a, $ ® 0$
a, 0 ® 00
e®1,a
b, $ ®1$
b,1®11
e®0,b
PDA M
)}()(:},{{)( *
wnwnbawML ba =Î=

57. © 2020 Wael Badawy
57
Time 0
Input
a ab b b
current
state
a
$
Stack
q1 q2
a, $ ® 0$
a, 0 ® 00
b, $ ®1$
b,1®11
Execution Example:
$$, ®e
e®1,a e®0,b

58. © 2020 Wael Badawy
58
Time 1
Input
a ab b b a
$
Stack
0
q1 q2
a, $ ® 0$
a, 0 ® 00
b, $ ®1$
b,1®11
$$, ®e
e®1,a e®0,b

59. © 2020 Wael Badawy
59
Time 3
Input
a bb b a
$
Stack
a
$
q1 q2
a, $ ® 0$
a, 0 ® 00
b, $ ®1$
b,1®11
0
$$, ®e
e®1,a e®0,b

60. © 2020 Wael Badawy
60
Time 4
Input
a bb b a
$
Stack
a
1
q1 q2
a, $ ® 0$
a, 0 ® 00
b, $ ®1$
b,1®11
$$, ®e
e®1,a e®0,b

61. © 2020 Wael Badawy
61
Time 5
Input
a bb b a
$
Stack
a
1
1
q1 q2
a, $ ® 0$
a, 0 ® 00
b, $ ®1$
b,1®11
$$, ®e
e®1,a e®0,b

62. © 2020 Wael Badawy
62
Time 6
Input
a bb b a
$
Stack
a
1
q1 q2
a, $ ® 0$
a, 0 ® 00
b, $ ®1$
b,1®11
1
$$, ®e
e®1,a e®0,b

63. © 2020 Wael Badawy
63
Time 7
Input
a bb b a
$
Stack
a
1
q1 q2
a, $ ® 0$
a, 0 ® 00
b, $ ®1$
b,1®11
$$, ®e
e®1,a e®0,b

64. © 2020 Wael Badawy
64
Time 8
Input
a bb b a a
$
Stack
q1 q2
a, $ ® 0$
a, 0 ® 00
b, $ ®1$
b,1®11
accept
$$, ®e
e®1,a e®0,b

65. 65
Formalities for PDAs
65

66. © 2020 Wael Badawy
66
q1 q2
21, wwa ®
)},{(),,( 2211 wqwaq =d
Transition function:

67. © 2020 Wael Badawy
67
q1
q221, wwa ®
q3
31, wwa ®
)},(),,{(),,( 332211 wqwqwaq =d
Transition function:

68. © 2020 Wael Badawy
Formal Definition
68
Pushdown Automaton (PDA)
),,,δ,Γ,Σ,( 0 FzqQM =
States
Input
alphabet
Stack
alphabet
Transition
function
Accept
states
Stack
start
symbol
Initial
state

69. © 2020 Wael Badawy
Instantaneous Description
69
),,( suq
Current
state
Remaining
input
Current
stack
contents

70. © 2020 Wael Badawy
70
q0 q1 q2 q3
Input
Stack
a a a b b b
$
a
aTime 4:
Example: Instantaneous Description
$),,( 1 aaabbbq
a
eee ®,
aa ®e,
e®ab,
e®ab,
$$, ®e

71. © 2020 Wael Badawy
71
q0 q1 q2 q3
Input
Stack
a a a b b b
$
a
aTime 5:
Example: Instantaneous Description
$),,( 2 aabbq
a
eee ®,
aa ®e,
e®ab,
e®ab,
$$, ®e

72. © 2020 Wael Badawy
72
We write:
$),,($),,( 21 aabbqaaabbbq !
Time 4 Time 5

73. © 2020 Wael Badawy
73
q0 q1 q2 q3
,$),(,$),($),,($),,(
$),,($),,($),,(
,$),(,$),(
3222
111
10
ee qqabqaabbq
aaabbbqaaabbbqaaabbbq
aaabbbqaaabbbq
!!!
!!!
!!
A computation:
eee ®,
aa ®e,
e®ab,
e®ab,
$$, ®e

74. © 2020 Wael Badawy
74
For convenience we write:
,$),(,$),( 30 eqaaabbbq
*
!
,$),(,$),($),,($),,(
$),,($),,($),,(
,$),(,$),(
3222
111
10
ee qqabqaabbq
aaabbbqaaabbbqaaabbbq
aaabbbqaaabbbq
!!!
!!!
!!

75. © 2020 Wael Badawy
Language of PDA
75
Language accepted by PDA :M
)},,(),,(:{)( 0 sqzwqwML f e
*
= !
Initial state Accept state
)(ML

76. © 2020 Wael Badawy
76
Example:
,$),(,$),( 30 eqaaabbbq
*
!
q0 q1 q2 q3
PDA :M
)(MLaaabbbÎ
eee ®,
aa ®e,
e®ab,
e®ab,
$$, ®e

77. © 2020 Wael Badawy
77
,$),(,$),( 30 eqbaq nn
*
!
q0 q1 q2 q3
)(MLba nn
Î
PDA :M
eee ®,
aa ®e,
e®ab,
e®ab,
$$, ®e

78. © 2020 Wael Badawy
78
q0 q1 q2 q3
PDA :M
}0:{)( ³= nbaML nnTherefore:
eee ®,
aa ®e,
e®ab,
e®ab,
$$, ®e