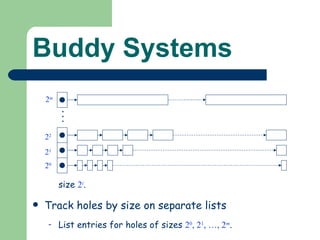
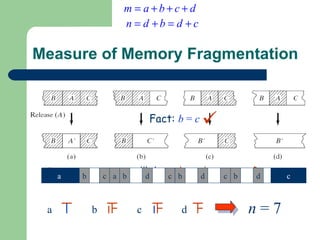
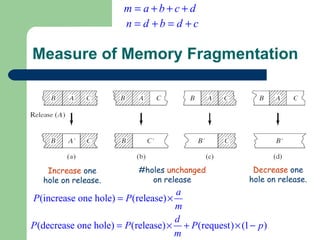
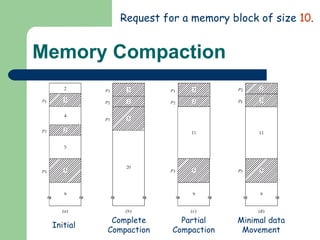
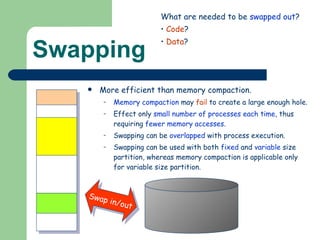
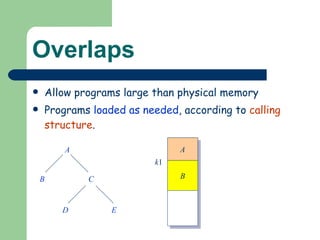
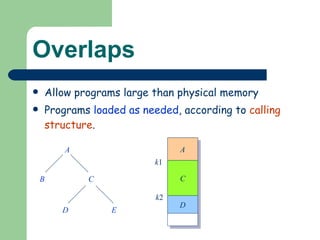
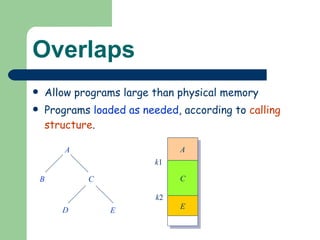
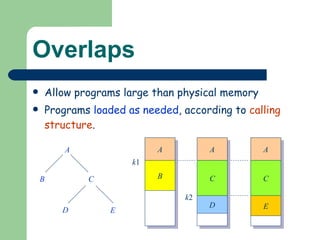
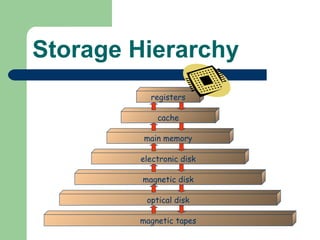
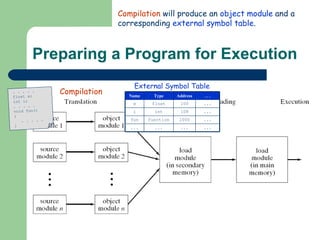
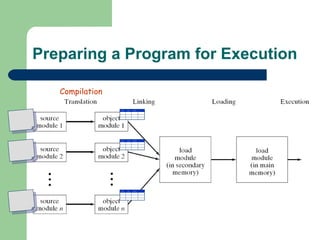
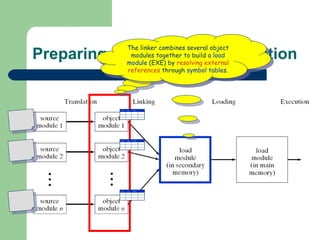
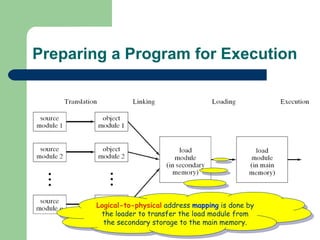
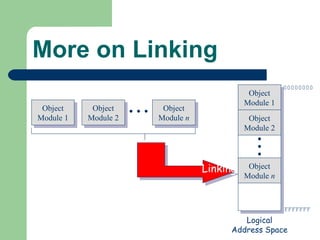
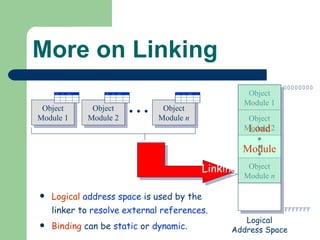
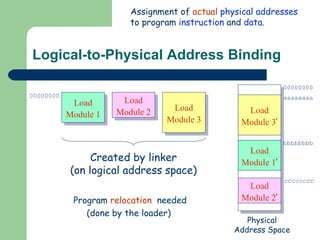
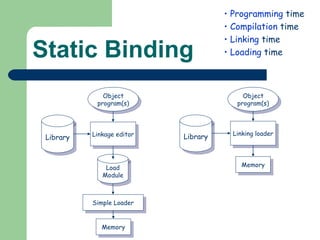
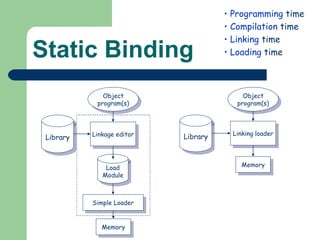
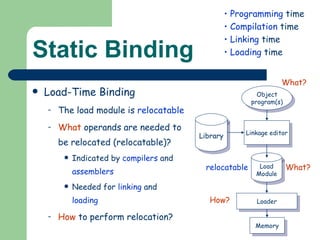
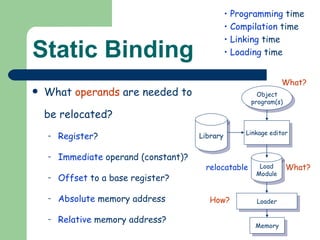
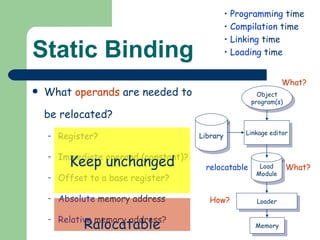
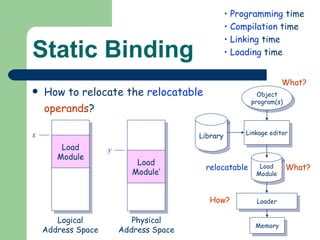
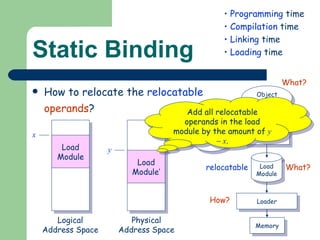
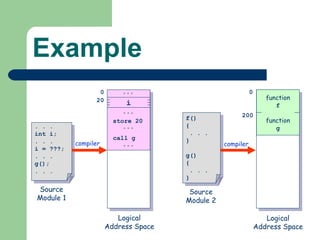
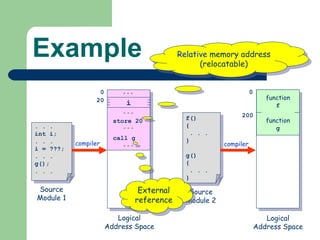
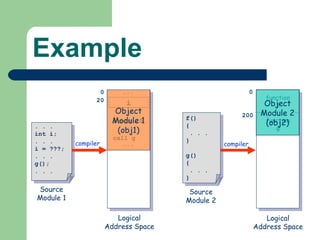
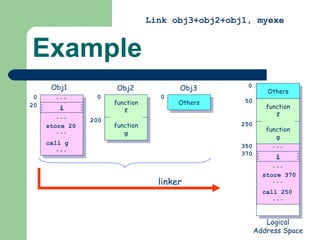
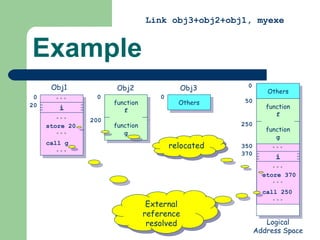
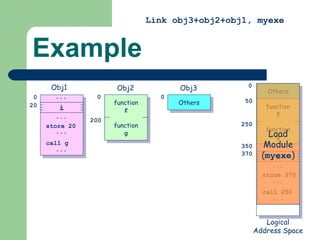
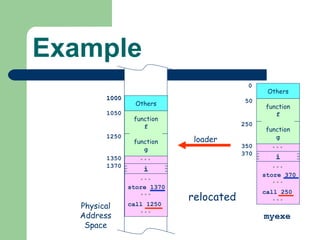
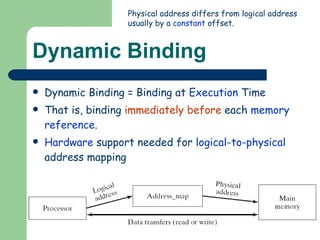
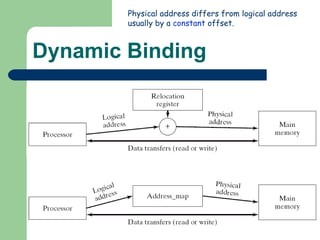
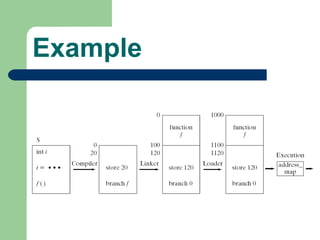
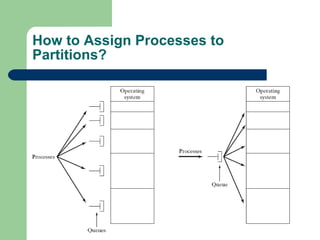
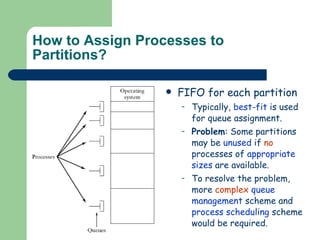
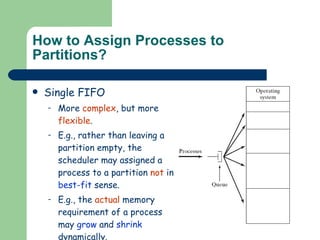
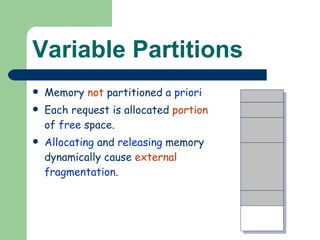
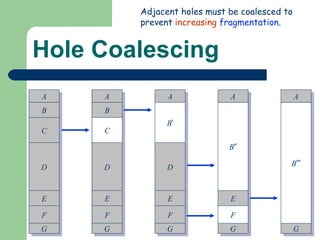
The document discusses different memory partitioning schemes used in operating systems. It describes fixed partitions where memory is divided into predetermined sized partitions at initialization time. It also describes variable partitions where memory is not pre-partitioned and is allocated on demand, which can cause external fragmentation. Dynamic binding is discussed where the logical to physical address mapping occurs at execution time with hardware support.

1. Operating Systems Principles Memory Management Lecture 7: Physical Memory 主講人：虞台文

2. Content Preparing a Program for Execution Program Transformations Logical-to-Physical Address Binding Memory Partitioning Schemes Fixed Partitions Variable Partitions Allocation Strategies for Variable Partitions Dealing with Insufficient Memory Memory Hierarchy

3. Operating Systems Principles Memory Management Lecture 7: Physical Memory Preparing a Program for Execution

4. Preparing a Program for Execution

5. Preparing a Program for Execution Modules reflecting different functions are designed separately, possibly by different programmers.

6. Preparing a Program for Execution Compilation External Symbol Table Compilation will produce an object module and a corresponding external symbol table .

7. Preparing a Program for Execution Compilation

8. Preparing a Program for Execution The linker combines several object modules together to build a load module (EXE) by resolving external references through symbol tables .

9. Preparing a Program for Execution Logical-to-physical address mapping is done by the loader to transfer the load module from the secondary storage to the main memory.

10. More on Linking Object Module 1 Object Module 2 Object Module n Logical Address Space Object Module 1 Object Module 2 Object Module n Linking 00000000 FFFFFFF

11. More on Linking Logical address space is used by the linker to resolve external references . Binding can be static or dynamic . Object Module 1 Object Module 2 Object Module n Logical Address Space Object Module 1 Object Module 2 Object Module n Linking Load Module 00000000 FFFFFFF

12. Logical-to-Physical Address Binding Load Module 1 Physical Address Space Load Module 2 Load Module 3 Load Module 3 ’ Load Module 2 ’ Load Module 1 ’ 00000000 Created by linker (on logical address space) 00000000 aaaaaaaa bbbbbbbb cccccccc Assignment of actual physical addresses to program instruction and data . Program relocation needed (done by the loader)

13. Address Binding Static binding Programming time Compilation time Linking time Loading time Dynamic binding Execution time Assignment of actual physical addresses to program instruction and data .

14. Static Binding Programming-time Binding Seldom used Used in low-level environments E.g., OS , real-time and embedded systems, control special hardware component. Programming time Compilation time Linking time Loading time

15. Static Binding SAMPLE PROGRAM FOR MC6802 USING CRS8 The following source file has been named MC6802.ASM CPU 6802 ; 6802 processor HOF MOT ; Motorola Records ORG 0100H ; Start of Data Source: DFB 'Hello and Welcome' Length: EQU $ - Source ;Length of Source Destin: DFS Length ; Buffer which has same ; length as Source ORG 0120H ; Start of Code Entry: LDX #Source ; Point Index Reg to ; Source string LDAB #Length ; Number of characters to move Loop: LDAA 0,X STAA Length,X INX DECB BNE Loop Fin: JMP Fin END Entry Programming-time binding Programming time Compilation time Linking time Loading time

16. Static Binding Compile-time Binding The compiler is given the starting address for the program to be load for execution. The resulting program can execute only when loaded into the specific preassigned memory space . Not relocatable Rarely used Programming time Compilation time Linking time Loading time

17. Static Binding Compile-time Binding Named variables have their addresses hardcoded Global variables given offset from start of global data area Local variables given offset from top of stack Object variables given offset from start of object data Normal function and method calls are hardcoded Normal functions have specific starting address in object file Object methods have specific starting address in object file Programming time Compilation time Linking time Loading time

18. Static Binding Link-time Binding The load module is still not relocatable The program will be loaded to memory with starting location specified or assumed by the linker ( Linkage Editor ). Linking loader : combining linking and loading Widely used in smaller, single user systems (e.g., CP/M) Programming time Compilation time Linking time Loading time

19. Static Binding Programming time Compilation time Linking time Loading time Object program(s) Linkage editor Library Simple Loader Memory Object program(s) Linking loader Memory Library Load Module

20. Static Binding Programming time Compilation time Linking time Loading time Object program(s) Linkage editor Library Simple Loader Memory Object program(s) Linking loader Memory Library Load Module

21. Static Binding Load-Time Binding The load module is relocatable What operands are needed to be relocated (relocatable)? Indicated by compilers and assemblers Needed for linking and loading How to perform relocation? Programming time Compilation time Linking time Loading time Object program(s) Linkage editor Library Loader Memory relocatable What? How? What? Load Module

22. Static Binding What operands are needed to be relocated? Register ? Immediate operand (constant)? Offset to a base register? Absolute memory address Relative memory address? Programming time Compilation time Linking time Loading time Object program(s) Linkage editor Library Loader Memory relocatable What? How? What? Load Module

23. Static Binding What operands are needed to be relocated? Register ? Immediate operand (constant)? Offset to a base register? Absolute memory address Relative memory address? Programming time Compilation time Linking time Loading time Object program(s) Linkage editor Library Loader Memory relocatable What? How? What? Keep unchanged Ralocatable Load Module

24. Static Binding How to relocate the relocatable operands ? Programming time Compilation time Linking time Loading time Object program(s) Linkage editor Library Loader Memory relocatable What? How? What? Logical Address Space Physical Address Space Load Module Load Module’ Load Module x y

25. Static Binding How to relocate the relocatable operands ? Object program(s) Linkage editor Library Loader Memory relocatable What? How? What? Logical Address Space Physical Address Space Load Module Load Module’ Add all relocatable operands in the load module by the amount of y  x . Programming time Compilation time Linking time Loading time Load Module x y

26. Example . . . int i; . . . i = ???; . . . g(); . . . Logical Address Space f() { . . . } g() { . . . } Logical Address Space Source Module 1 Source Module 2 0 20 i store 20 call g 0 200 function f function g compiler compiler

27. Example . . . int i; . . . i = ???; . . . g(); . . . Logical Address Space f() { . . . } g() { . . . } Logical Address Space Source Module 1 Source Module 2 Relative memory address (relocatable) External reference 0 20 i store 20 call g 0 200 function f function g compiler compiler

28. Example . . . int i; . . . i = ???; . . . g(); . . . Logical Address Space f() { . . . } g() { . . . } Logical Address Space Source Module 1 Source Module 2 Object Module 1 (obj1) Object Module 2 (obj2) 0 20 i store 20 call g 0 200 function f function g compiler compiler

29. Example Obj1 Obj2 Obj3 Link obj3+obj2+obj1, myexe Logical Address Space 0 20 i store 20 call g 0 200 function f function g 0 Others 0 Others 50 250 function f function g 350 370 i store 370 call 250 linker

30. Example Obj1 Obj2 Obj3 Link obj3+obj2+obj1, myexe Logical Address Space relocated External reference resolved 0 20 i store 20 call g 0 200 function f function g 0 Others 0 Others 50 250 function f function g 350 370 i store 370 call 250

31. Example Obj1 Obj2 Obj3 Logical Address Space Load Module ( myexe ) Link obj3+obj2+obj1, myexe 0 20 i store 20 call g 0 200 function f function g 0 Others 0 Others 50 250 function f function g 350 370 i store 370 call 250

32. Example myexe Physical Address Space 1000 1000 relocated 0 Others 50 250 function f function g 350 370 i store 370 call 250 Others 1050 1250 function f function g 1350 1370 i store 1370 call 1250 loader

33. Dynamic Binding Dynamic Binding = Binding at Execution Time That is, binding immediately before each memory reference. Hardware support needed for logical-to-physical address mapping Physical address differs from logical address usually by a constant offset.

34. Dynamic Binding Physical address differs from logical address usually by a constant offset.

35. Example

36. Operating Systems Principles Memory Management Lecture 7: Physical Memory Memory Partitioning Schemes

37. Memory Partitioning Schemes Fixed Partitions The number of partitions and the size of each partition are determined at the time the OS is initialized . Variable Partitions Memory not partitioned a priori Partitioning on demand

38. Fixed Partitions Single-program systems 2 partitions (OS/user) Multi-programmed systems partitions of different sizes OS User OS . . .

39. How to Assign Processes to Partitions?

40. How to Assign Processes to Partitions? FIFO for each partition Typically, best-fit is used for queue assignment. Problem : Some partitions may be unused if no processes of appropriate sizes are available. To resolve the problem, more complex queue management scheme and process scheduling scheme would be required.

41. How to Assign Processes to Partitions? Single FIFO More complex , but more flexible . E.g., rather than leaving a partition empty, the scheduler may assigned a process to a partition not in best-fit sense. E.g., the actual memory requirement of a process may grow and shrink dynamically.

42. Limitations of Fixed Partitions Program size limited to largest partition Internal fragmentation unused space within partitions OS

43. Variable Partitions Memory not partitioned a priori Each request is allocated portion of free space. Allocating and releasing memory dynamically cause external fragmentation .

44. Issues How to allocate memories of sizes All free blocks are applicable . None free block is applicable . But, the total amount of free memory is large enough . Allocate which one? Over time, memory will consist a sequence of variable size blocks . Some are free , and some are not .

45. Hole Coalescing A B D E C F A B D E C F A B D E C F B ’ A D E F B ’ B ’’ G G G G A E F B ’’ G B ’’’ Adjacent holes must be coalesced to prevent increasing fragmentation .

46. Hole Coalescing Adjacent holes must be coalesced to prevent increasing fragmentation . Four cases on hole coalescing: no adjacent hole A hole at right A hole at left Holes at two sides

47. Link List Implementation (I) Free blocks are kept sorted using a doubly linked list . What would be done to release a block of memory? Check both its neighbors for possible coalescing . Problems: How to check the right neighbor? How to check the left neighbor? G A B C D E F free free free occupied occupied occupied occupied size size size size size size size easy checked by starting from the header ( inefficient )

48. Link List Implementation (II) Free blocks are linked using a doubly linked list need not be sorted What would be done to release a block of memory? Check both its neighbors for possible coalescing . Problems: How to check the right neighbor? How to check the left neighbor? E A B free occupied size size free size occupied size C occupied size occupied size D occupied size occupied size free size easy easy

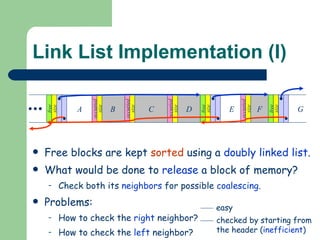
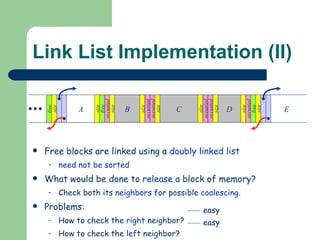
49. Bitmap Implementation Memory divided into fix-size blocks Each block represented by a 0/1 bit in a binary string: the “ bitmap ” Can be implemented as char or int array Operations use bit masks Release : B[i] = B[i] & '11011111' Allocate : B[i] = B[i] | '11000000' Search : Repeatedly, Check left-most bit and Shift mask right: TEST = B[i] & '10000000' Free Allocated

50. Bitmap Implementation Memory divided into fix-size blocks Each block represented by a 0/1 bit in a binary string: the “ bitmap ” Can be implemented as char or int array Operations use bit masks Release : B[i] = B[i] & '11 0 11111' Allocate : B[i] = B[i] | ' 11 000000' Search : Repeatedly, Check left-most bit and Shift mask right: TEST = B[i] & ' 1 0000000'

51. Bitmap Implementation 4K 00000000 4K 4K 4K 4K 4K 4K 4K 4K 4K 4K 4K 4K 4K 4K 4K 00001000 00002000 00003000 00004000 00005000 00006000 00007000 00008000 00009000 0000a000 0000b000 0000c000 0000d000 0000e000 0000f000 4K 00010000 4K 4K 4K 4K 4K 4K 4K 4K 4K 4K 4K 4K 4K 4K 4K 00011000 00012000 00013000 00014000 00015000 00016000 00017000 00018000 00019000 0001a000 0001b000 0001c000 0001d000 0001e000 0001f000 4K 00070000 4K 4K 4K 4K 4K 4K 4K 4K 4K 4K 4K 4K 4K 4K 4K 00071000 00072000 00073000 00074000 00075000 00076000 00077000 00078000 00079000 0007a000 0007b000 0007c000 0007d000 0007e000 0007f000                                                

52. Bitmap Implementation 4K 4K 4K 4K 4K 4K 4K 4K 4K 4K 4K 4K 4K 4K 4K 4K 4K 4K How to allocate a block of continuous memory of a given size? 4K 00000000 4K 4K 4K 4K 4K 4K 4K 4K 4K 4K 4K 4K 4K 4K 4K 00001000 00002000 00003000 00004000 00005000 00006000 00007000 00008000 00009000 0000a000 0000b000 0000c000 0000d000 0000e000 0000f000 4K 00010000 4K 4K 4K 4K 4K 4K 4K 4K 4K 4K 4K 4K 4K 4K 4K 00011000 00012000 00013000 00014000 00015000 00016000 00017000 00018000 00019000 0001a000 0001b000 0001c000 0001d000 0001e000 0001f000 4K 00070000 4K 4K 4K 4K 4K 4K 4K 4K 4K 4K 4K 4K 4K 4K 4K 00071000 00072000 00073000 00074000 00075000 00076000 00077000 00078000 00079000 0007a000 0007b000 0007c000 0007d000 0007e000 0007f000                                                

53. Buddy Systems Compromise between fixed and variable partitions Fixed number of possible hole sizes ; typically, 2 i . Each hole of size 2 i can be divided (equally) into 2 buddies of size 2 i  1 . Two buddies can be combined into the original hole of size 2 i . Track holes by size on separate lists List entries for holes of sizes 2 0 , 2 1 , …, 2 m . 2 i 2 i  1 2 i  1

54. Buddy Systems Compromise between fixed and variable partitions Fixed number of possible hole sizes ; typically, 2 i . Each hole of size 2 i can be divided (equally) into 2 buddies of size 2 i  1 . Two buddies can be combined into the original hole of size 2 i . Track holes by size on separate lists List entries for holes of sizes 2 0 , 2 1 , …, 2 m . . . . 2 0 2 1 2 2 2 m

55. Buddy Systems When n bytes requested , find smallest i so that n  2 i If hole of this size available , allocate it; otherwise , consider larger holes. Recursively split each hole into two buddies until smallest adequate hole is created Allocate it and place other holes on appropriate lists On release , recursively coalesce buddies Buddy searching for coalescing can be inefficient

56. Example void p= malloc (1*blocksize); free (12*blocksize); Hole Sizes: 1, 2, 4, 8, 16 3 blocks allocated & 3 holes left

57. Operating Systems Principles Memory Management Lecture 7: Physical Memory Allocation Strategies for Variable Partitions

58. Allocation Strategies Problem: Given a request for n bytes, find hole ≥ n Goal: Maximize memory utilization ( Minimize “ external fragmentation ”) Minimize search time

59. Common Allocation Strategies First-fit: Always start from the beginning of free-list Simplest Generally the best choice Next-fit: Rotating-first-fit (Resume search) Improves distribution of holes Best-fit: Closest fit Avoid breaking up large holes. Worst-fit: Largest fit Avoid leaving tiny hole fragments

60. Measure of Memory Fragmentation What measurement could be used?

61. Measure of Memory Fragmentation What measurement could be used? m : #blocks occupied n : #holes

62. Measure of Memory Fragmentation What measurement could be used? m : #blocks occupied n : #holes

63. Measure of Memory Fragmentation What measurement could be used? m : #blocks occupied n : #holes Four types of occupied memory blocks. Increase one hole on release. #holes unchanged on release Decrease one hole on release.

64. Measure of Memory Fragmentation What measurement could be used? m : #blocks occupied n : #holes Increase one hole on release. #holes unchanged on release Decrease one hole on release. Let a , b , c , d be the average number of occupied blocks of each type in memory during equilibrium . Fact: b = c

65. Measure of Memory Fragmentation Increase one hole on release. #holes unchanged on release Decrease one hole on release. Fact: b = c

66. Measure of Memory Fragmentation Increase one hole on release. #holes unchanged on release Decrease one hole on release. Fact: b = c b c a b d c b d c b d a b c d 

67. Measure of Memory Fragmentation Increase one hole on release. #holes unchanged on release Decrease one hole on release. Fact: b = c b c a b d c b d c b d a b c d a c  n = 7

68. Measure of Memory Fragmentation Increase one hole on release. #holes unchanged on release Decrease one hole on release.

69. Measure of Memory Fragmentation Increase one hole on release. #holes unchanged on release Decrease one hole on release. p : The probability that the request memory size doesn’t match any hole size. Fact: p  1 .

70. Measure of Memory Fragmentation In equilibrium,

71. Measure of Memory Fragmentation In equilibrium, 50% rule (Knuth 1968) In Equilibrium, of the total number of occupied blocks and holes , 1/3 are holes.

72. Measure of Memory Utilization In equilibrium, 50% rule (Knuth 1968) In Equilibrium, of the total number of occupied blocks and holes , 1/3 are holes. How much memory is wasted? (average) hole_size is not the same as (average) block_size

73. Measure of Memory Utilization Assume b : average block size h : average hole size

74. Measure of Memory Utilization Assume b : average block size h : average hole size 50% rule (Knuth 1968)

75. Measure of Memory Utilization Assume b : average block size h : average hole size We want to minimize the value of f. It is equivalent to minimize k . How to know the value of k ?

76. Measure of Memory Utilization Simulations by Knuth (1968) provide an answer. k depends on the ratio of b / M , e.g., b  M /10 , k = 0.22  f  0.1 b  M /3 , k = 2  f  0.5 Assume b : average block size h : average hole size How to know the value of k ?

77. Measure of Memory Utilization Assume b : average block size h : average hole size Conclusion: M must be large relative to b , otherwise much of main memory will remain unused.

78. Operating Systems Principles Memory Management Lecture 7: Physical Memory Dealing with Insufficient Memory

79. Managing Insufficient Memory What to be done? when the total size of free memory is large enough while the memory requirement of a process exceeds the size of the largest partition when new process arrives with insufficient free memory? When the memory requirement is larger than the physical memory size .

80. Dealing with Insufficient Memory Memory compaction How much and what to move? Swapping Temporarily move process to disk Requires dynamic relocation Overlays Allow programs larger than physical memory Programs loaded as needed according to calling structure .

81. Memory Compaction Request for a memory block of size 10 . Initial Complete Compaction Partial Compaction Minimal data Movement

82. Swapping More efficient than memory compaction. Memory compaction may fail to create a large enough hole. Effect only small number of processes each time , thus requiring fewer memory accesses . Swapping can be overlapped with process execution. Swapping can be used with both fixed and variable size partition, whereas memory compaction is applicable only for variable size partition. Swap in/out What are needed to be swapped out ? Code ? Data ?

83. Overlaps Allow programs large than physical memory Programs loaded as needed , according to calling structure . A B C D E A k 1 B

84. Overlaps Allow programs large than physical memory Programs loaded as needed , according to calling structure . A B C D E A k 1 B C k 2 D

85. Overlaps Allow programs large than physical memory Programs loaded as needed , according to calling structure . A B C D E A k 1 B C k 2 D E

86. Overlaps Allow programs large than physical memory Programs loaded as needed , according to calling structure . A B C D E A k 1 B A C k 2 D A B C E

87. Operating Systems Principles Memory Management Lecture 7: Physical Memory Memory Hierarchy

88. Storage Hierarchy registers cache main memory electronic disk magnetic disk optical disk magnetic tapes

89. Storage Hierarchy registers cache main memory electronic disk magnetic disk optical disk magnetic tapes Speed Size

90. Memory Hierarchy Design Principles Make the Common Case Fast Principle of Locality Smaller is Faster