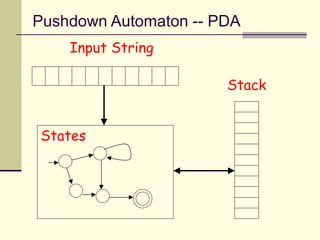
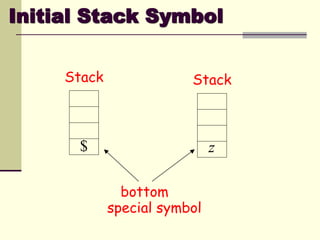
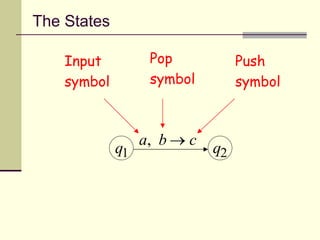
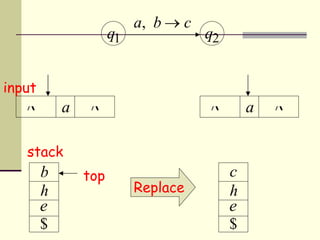
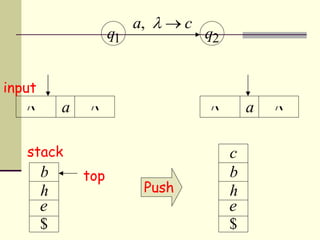
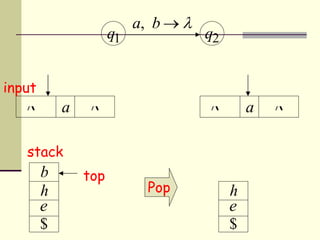
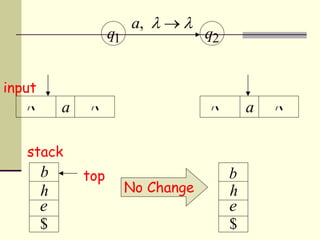
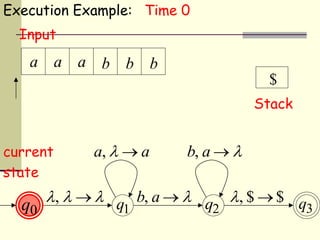
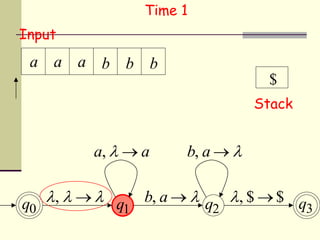
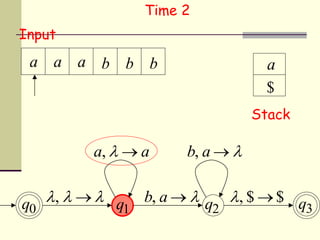
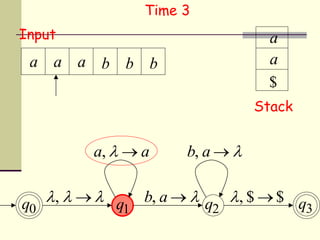
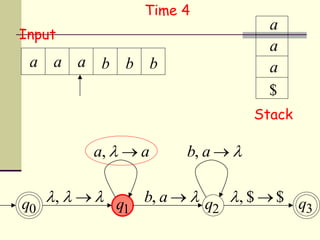
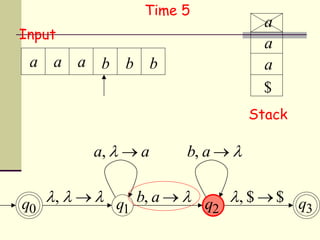
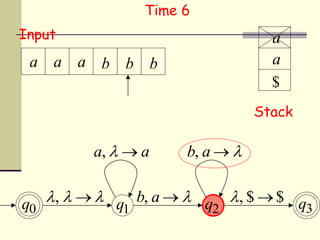
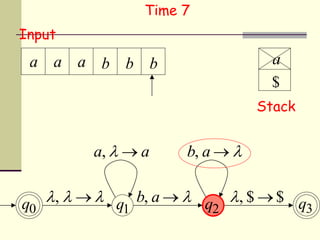
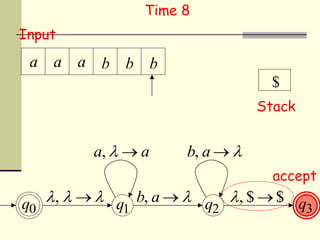
This presentation introduces pushdown automata (PDA). A PDA is a nondeterministic finite state automaton that has an additional stack. It can perform epsilon transitions and manipulate symbols on the stack. PDAs have states, an initial stack symbol, and transitions that can pop, push or replace symbols on the stack. The presentation provides an example of a nondeterministic PDA and traces its execution on an input string to demonstrate how it works. A string is accepted if the PDA reaches a final state after consuming all input, regardless of the stack contents.

1. WELCOME
OUR PRESENTATION

2. Our Topic
PDA (pushdown automaton)

3. GROUP MEMBER
NAME S.ID
Zaheer Raihan
Shah Alam Shagor
011151053
011151052

4. Pushdown Automaton
(PDA)
A Pushdown Automaton is a nondeterministic
finite state automaton (NFA) that permits
ε-transitions and a stack.

5. Pushdown Automaton -- PDA
Input String
Stack
States

6. Initial Stack Symbol
Stack
$
Stack
z
bottom
special symbol

7. The States
q1 q2
a, b  c
Input
symbol
Pop
symbol
Push
symbol

8. q1 q2
a, b  c
a 
b top
input
stack
a 
Replace
e
h
$
e
h
$
c

9. q1 q2
a,   c
a  a 
Push
b
e
h
$
e
h
$
b
c
top
input
stack

10. q1 q2
a, b  
a  a 
Pop
b
e
h
$
e
h
$
top
input
stack

11. q1 q2
a,   
a  a 
No Change
b
e
h
$
e
h
$
btop
input
stack

12. Non-Determinism
q1
q2a, b  c
q3
a, b  c
q1 q2
, b  c
transition
These are allowed transitions in
a Non-deterministic PDA (NPDA)

13. NPDA: Non-Deterministic PDA
Example:
,   
a,   a
b, a  q0 q1 q2 q3
b, a  
, $  $

14. a,   a
b, a  
0q q1 q2 q3
Execution Example:
Input
a a a b b b
current
state
b, a  
Time 0
,    , $  $
Stack
$

15. a,   a
b, a  q0 q1 q2 q3
Input
a a a b b b
b, a  
Time 1
,    , $  $
Stack
$

16. a,   a
b, a  q0 q1 q2 q3
Input
Stack
a a a b b b
$
a
b, a  
Time 2
,    , $  $

17. a,   a
b, a  q0 q1 q2 q3
Input
Stack
a a a b b b
$
a
a
b, a  
Time 3
,    , $  $

18. a,   a
b, a  q0 q1 q2 q3
Input
Stack
a a a b b b
$
a
a
a
b, a  
Time 4
,    , $  $

19. a,   a
b, a  q0 q1 q2 q3
Input
a a a b b b
Stack
$
a
a
a
b, a  
Time 5
,    , $  $

20. a,   a
b, a  q0 q1 q2 q3
Input
a a a b b b
$
a
Stack
b, a  
Time 6
,    , $  $
a

21. a,   a
b, a  q0 q1 q2 q3
Input
a a a b b b
$
Stack
b, a  
Time 7
,    , $  $
a

22. a,   a
b, a  q0 q1 q2 q3
Input
a a a b b b
b, a  
Time 8
accept
,    , $  $
$
Stack

23. A string is accepted if there is
a computation such that:
• All the input is consumed
• The last state is a final state
At the end of the computation,
we do not care about the stack contents
The Language of PDA

24. ANY
QUESTION
????????

25. THE
END