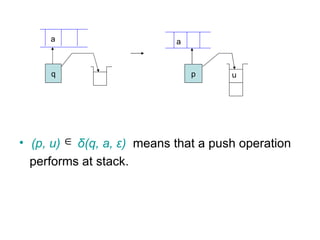
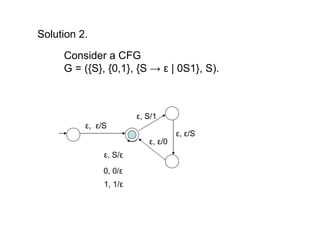
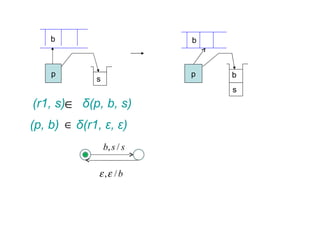
The document describes pushdown automata (PDA). A PDA has a tape, stack, finite control, and transition function. It accepts or rejects strings by reading symbols on the tape, pushing/popping symbols on the stack, and changing state according to the transition function. The transition function defines the possible moves of the PDA based on the current state, tape symbol, and stack symbol. If the PDA halts in a final state with an empty stack, the string is accepted. PDAs can recognize any context-free language. Examples are given of PDAs for specific languages.

1. Lecture Pushdown Automata

2. tape
tape head
stack head
finite
stack
control

3. a l p h a b e t
The tape is divided into finitely many cells.
Each cell contains a symbol in an alphabet
Σ.

4. The stack head always scans the top
symbol of the stack. It performs two
basic operations:
Push: add a new symbol at the top.
Pop: read and remove the top symbol.
Alphabet of stack symbols: Γ

5. a
• The head scans at a cell on the tape and
can read a symbol on the cell. In each
move, the head can move to the right cell.

6. • The finite control has finitely many states
which form a set Q. For each move, the
state is changed according to the
evaluation of a transition function
Q x (Γ U {ε})
δ : Q x (Σ U {ε}) x (Γ U {ε}) → 2 .

7. a a
q v p u
• (p, u) ∈ δ(q, a, v) means that if the tape head
reads a, the stack head read v, and the finite
control is in the state q, then one of possible
moves is that the next state is p, v is replaced
by u at stack, and the tape head moves one cell
to the right.

8. a a
q v p u
• (p, u) ∈ δ(q, ε, v) means that this a ε-move.

9. a a
q p u
• (p, u) ∈ δ(q, a, ε) means that a push operation
performs at stack.

10. a a
q v p
• (p, ε) ∈ δ(q, a, v) means that a pop operation
performs at stack

11. s
• There are some special states: an initial
state s and a final set F of final states.
• Initially, the PDA is in the initial state s and
the head scans the leftmost cell. The tape
holds an input string. The stack is empty.

12. x
f
• When the head gets off the tape, the PDA
stops. An input string x is accepted by the
PDA if the PDA stops at a final state and
the stack is empty.
• Otherwise, the input string is rejected.

13. • The PDA can be represented by
M = (Q, Σ, Γ, δ, s, F)
where Σ is the alphabet of input symbols
and Γ is the alphabet of stack symbols.
• The set of all strings accepted by a PDA M
is denoted by L(M). We also say that the
language L(M) is accepted by M.

14. • The transition diagram of a PDA is an
alternative way to represent the PDA.
• For M = (Q, Σ, Γ, δ, s, F), the transition diagram
of M is an edge-labeled digraph G=(V, E)
satisfying the following:
V = Q (s = ,f= for f ∈ F)
a, v/u
E={q p | (p,u) ∈ δ(q, a, v) }.

15. Example 1. Construct PDA to accept
n n
L= {0 1 | n > 0}
Solution 1.
1, 0/ε
0, ε/0 1, 0/ε

16. Solution 2.
Consider a CFG
G = ({S}, {0,1}, {S → ε | 0S1}, S).
ε, S/1
ε, ε/S
ε, ε/S
ε, ε/0
ε, S/ε
0, 0/ε
1, 1/ε

17. Theorem Every CFL can be accepted by a PDA.
Proof. Consider a CFL L = L(G) for a CFG
G = (V, Σ, R, S).
ε, A/xn A → x1 x2 …xn in R
ε, ε/S
ε, ε/x1
a, a/ε for a in Σ
Theorem
A language L is CFL ⇔ it can be accepted by a PDA.

18. Sometimes, constructing the PDA is easier than
constructing CFG.

19. Example 2
Show that {x ∈ {a, b} | #b ( x) ≤ # a ( x) ≤ 2#b ( x)} is a CFL
Construct a PDA or a CFG?
PDA!!!
Sometimes, constructing the PDA is easier than
constructing CFG.

20. Idea
To check if #b ( x) ≤ # a ( x) ≤ 2#b ( x), we need to cancel a with b.
For each b, we need to cancel sometimes one a and sometimes
two a. Do we need to make a deterministic choice at each
cancellation? No, the concept of nondeterministic computation
solves this trouble : As long as a correct choice exists, the input
string x would be accepted!

21. a a
s p s
• (p, s) ∈ δ(s, ε, ε)
ε ,ε / s

22. a a
p p a
s
s
(q, s) ∈ δ(p, a, s)
(p, a) ∈ δ(q, ε, ε)
a, s / s
ε ,ε / a

23. a a
p p a
a
a
∈
(q1, a) δ(p, a, a)
(p, a) ∈ δ(q1, ε, ε)
a, a / a
ε ,ε / a

24. a a
p p
b
(p, ε) ∈ δ(p, a, b)
a,b / ε

25. a a
p p b’
b
(p, b’)∈ δ(p, a, b)
a, b / b'

26. a a
p p
b’
(p, ε) ∈ δ(p, a, b’)
a,b' / ε

27. b b
p p b
s
s
(r1, s)∈ δ(p, b, s)
(p, b) ∈ δ(r1, ε, ε)
b, s / s
ε ,ε / b

28. b b
p p b
b
b
(r2, b)∈ δ(p, b, b)
(p, b) ∈ δ(r2, ε, ε)
b, b / b
ε ,ε / b

29. b b
p p b
b’
b’
(r3, b’) ∈ δ(p, b, b’)
(p, b) ∈ δ(r3, ε, ε)
b, b' / b'
ε ,ε / b

30. b b
p p
a
(p, ε) ∈ δ(p, b, a)
b, a / ε

31. b b
p p
a
a
(t, ε) ∈ δ(p, b, a) (p, ε) ∈ δ(t, ε, a)
b, a / ε
ε,a /ε

32. b b
p p b’
a
z z
z≠a
(t, ε) ∈ δ(p, b, a) (u, x) ∈ δ(t, ε, x) (p, b’)∈ δ(u, ε, ε)
b, a / ε
ε, z / z
ε ,b' / ε z≠a

33. p p
s
(p, ε) ∈ δ(p, ε, s)
ε,s /ε

34. a,b / ε
a, b / b'
a,b' / ε
ε ,ε / s a, z / z
z ≠ b,b'
ε ,ε / a
ε,s /ε
b, a / ε
b, a / ε b, z / z
z≠a
ε,a /ε
ε, z / z ε ,ε / b
z≠a ε , ε / b'

35. Example 3
Construct PDA accepting {x ∈ {a, b} | #b ( x) <# a ( x) ≤ 2#b ( x)}.
Idea
To have #b ( x) <# a ( x), we must have a b which cancel two a ' s.
Let the first b do the job.

36. a,b / ε
Solution
a, b / b' a, z / z
a,b' / ε 1
z ≠ b,b'
ε ,ε / s a, b / b' a, z / z
11 z ≠ b,b' ε ,ε / a
b, a / ε ε,a /ε
ε , ε / b'
ε ,ε / a
ε, z / z
z≠a ε,s /ε
b, a / ε
b, a / ε b, z / z
z≠a
b, z / z
ε,a /ε 1
ε, z / z ε ,ε / b z≠a
z≠a ε , ε / b'
ε ,ε / b

37. Example 4
Construct PDA accepting {x ∈ {a, b} | #b ( x) ≤# a ( x) < 2#b ( x)}.
Idea
To have # a ( x) < 2#b ( x), we must have a b which cancel one a.
Let the first b do the job.

38. a,b / ε
Solution
a, b / b' a, z / z
a,b' / ε 1
z ≠ b,b'
ε ,ε / s a,b / ε a, z / z
1
1
z ≠ b,b' ε ,ε / a
b, a / ε
ε ,ε / a
ε,s /ε
b, a / ε
b, a / ε b, z / z
z≠a
b, z / z
ε,a /ε 1
ε, z / z ε ,ε / b z≠a
z≠a ε , ε / b'
ε ,ε / b