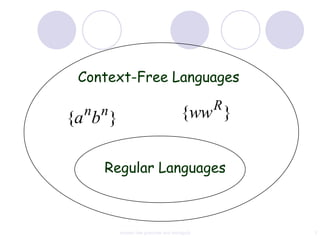
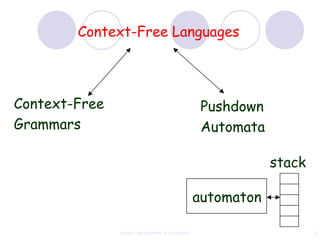
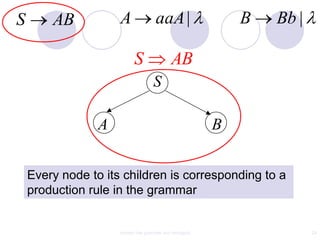
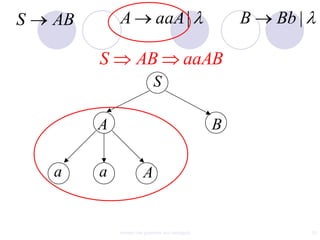
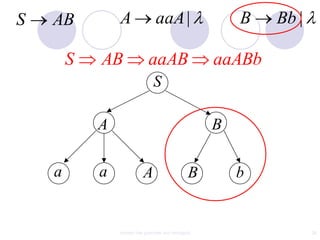
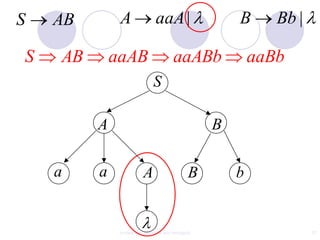
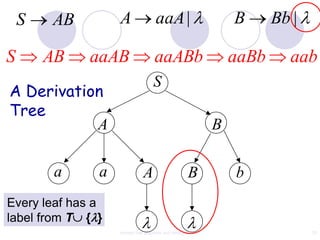
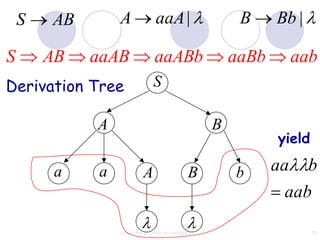
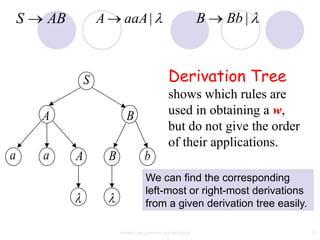
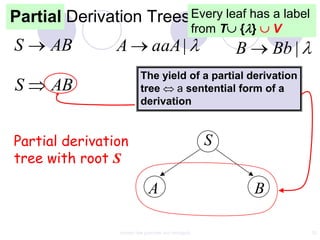
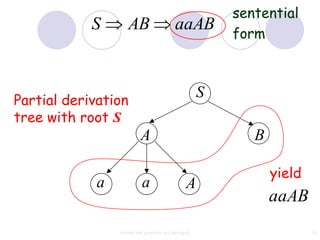
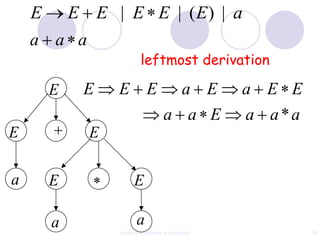
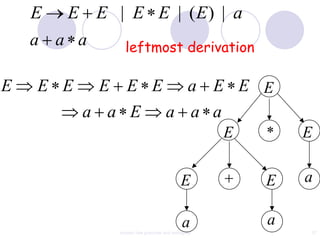
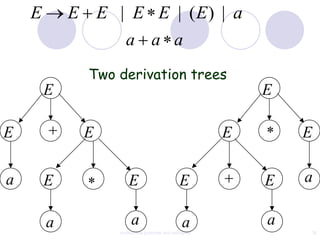
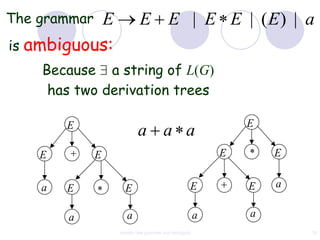
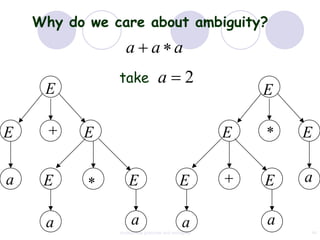
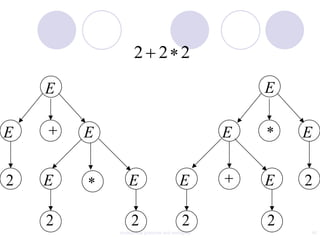
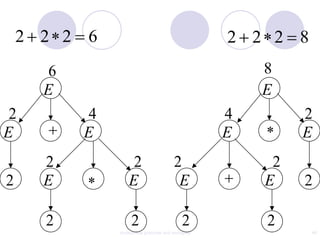
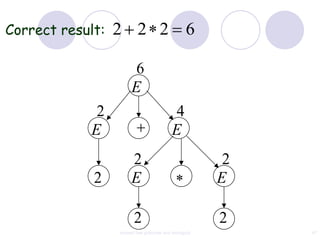
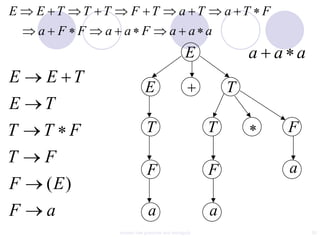
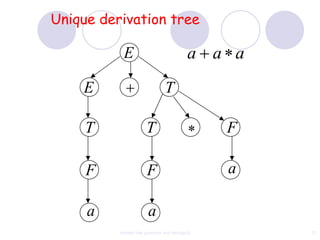
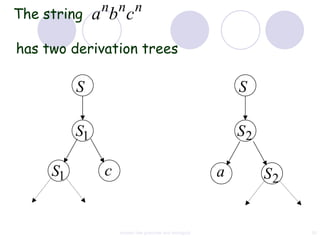
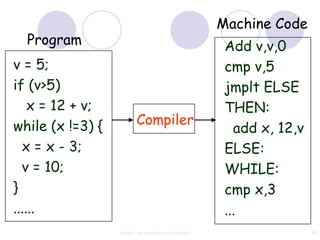
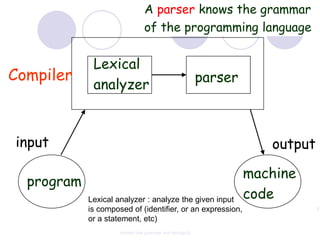
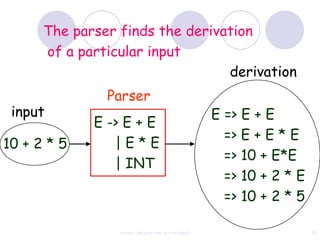
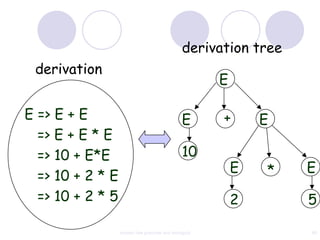
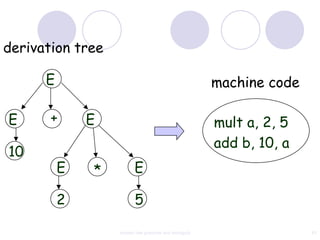
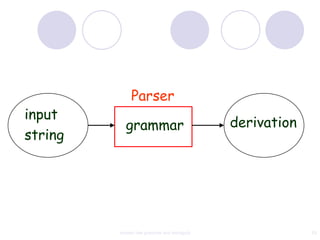
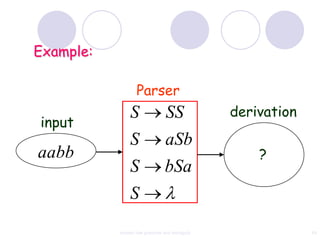
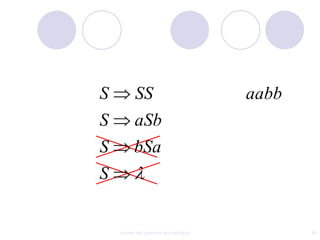
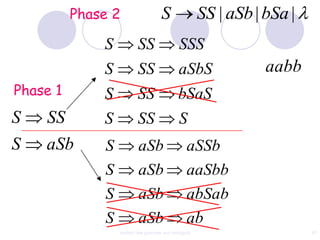
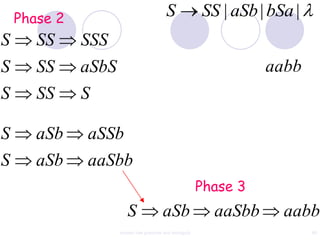
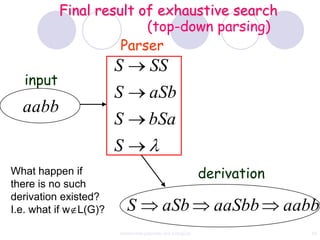
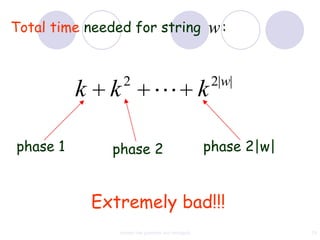
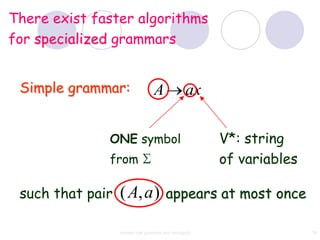
This document discusses context-free grammars and ambiguity. It provides examples of context-free grammars and their derivations using derivation trees. A context-free grammar is ambiguous if some string in the language has two or more derivation trees. Ambiguity is undesirable for programming languages as it leads to parsing ambiguities. To remove ambiguity, an ambiguous grammar can be modified to produce a non-ambiguous grammar.

1. Context-Free Languages
Derivation tree, parsing, & ambiguity
context free grammar and ambiguity 1

2. n n R
{a b } {ww }
Regular Languages
context free grammar and ambiguity 2

3. Context-Free Languages
n n R
{a b } {ww }
Regular Languages
context free grammar and ambiguity 3

4. Context-Free Languages
Context-Free Pushdown
Grammars Automata
stack
automaton
context free grammar and ambiguity 4

5. Context-Free Grammars
context free grammar and ambiguity 5

6. n n
L(G ) {a b : n 0} is not regular ….
(((( ))))
we relax the restriction of regular grammar
context free grammar and ambiguity 6

7. n n
L(G ) {a b : n 0} is not regular ….
A context-free grammar G : S aSb
S
The grammar G is linear but not regular.
context free grammar and ambiguity 7

8. n n
L(G ) {a b : n 0} is not regular ….
Regular grammar (e.g., a right linear grammar):
A XB or A  X
where A, B V, and X T*
Context Free
A  X where X (V T)* Grammar
context free grammar and ambiguity 8

9. Def. Context-Free Grammars (CFG)
Grammar G (V , T , S , P )
Variables Terminal Start
symbols variable
Productions of the form: A x
x is string of variables and terminals
Note: A regular grammar is a regular grammar.
context free grammar and ambiguity 9

10. Def. Context-Free Languages (CFL)
A language L is context-free
if and only if
there is a context free grammar G
with L L (G )
Note: To show L is a CFL find a CFG for L.
Note: A regular language is also a CFL.
context free grammar and ambiguity 10

11. n n is a Context-Free
L(G ) {a b : n 0} Language
with context-free grammar G: S aSb
S
A derivation:
S aSb aaSbb aaaSbbb aaabbb
context free grammar and ambiguity 11

12. Another Example
A context-free grammar G: S aSa
S bSb
A derivation: S
S aSa abSba abaSaba abaaba
R
L(G ) {ww : w {a, b}*}
is a Context-Free Language
context free grammar and ambiguity 12

13. A non Linear Examples
A context-free grammar G: S aSb
S SS
S
What is the L(G)?
A derivation:
S SS aSbS abS abaSb
abaaSbb abaabb () (( ))
context free grammar and ambiguity 13

14. S aSb
S SS
S () ((( ))) (( ))
L(G ) {w : na ( w) nb ( w), and
na (v) nb (v) in any prefix v}
How to prove the given grammar
indeed generates the language?
Homework #4 only shows L(G) L.
context free grammar and ambiguity 14

15. L(G) L: by induction on the number of steps in deriving a sentential form
Any sentential form obtained from the grammar G: if by one step (rule2 & 3
do not generate any terminal symbols at all, i.e. na(w)=nb(w) = 0, thus is
true; if it is from rule 1: SaSb, then it satisfies the condition of
na(w)=nb(w) and the prefix condition.
Assume any sentential obtained from n steps it is true,
Now assume a sentential form of (n+1) steps: if the last step is by rule 2 or
3, then no new symbols is added, therefore it satisfies the condition since
it satisfies on previous step; it the last step is by rule 1, then as can be
seen that a is added before b is added (from left to right), thus the prefix
condition is also satisfied.
L L(G): by induction on |w|, w L.
By observing the definition of L, w L then |w| is even, let |w|=2n. and if
|w| >= 2, w = a…..b (the first symbol is a and the last symbol is b).
|w|=0: then w= , then w L(G).
Assume |w|=2n, w L(G) is true for n >= 0.
Now |w| = 2n+2, then w=aub with |u|=2n, and u L. by induction
assumption, u L(G), i.e. there exist a derivation s * u, thus S aSb *
aub = w.
context free grammar and ambiguity 15

16. Show L={anbmcn: n, m 0 } is CF.
Show L={anbncm: n, m 0 } is CF.
context free grammar and ambiguity 16

17. True or False
If L is not regular then L is context
free.
If L is not context free then L is not
regular
From grammar
G: S AB, A aA| , B bB| , thus
L(G) is CF & not regular.
context free grammar and ambiguity 17

18. Examples of showing languages are
Context Free
Show { anbm : n = m+3} is CF.
Show { anbm : n m+3} is CF.
Try hw # 7 (a) ~ (d) p.133
context free grammar and ambiguity 18

19. {anbm: n m+3}
S1 is for n> m+3 & S2 is for n < m+3 & S  S1
| S2
S1: n m+4, i.e., n = m+t for t=4, 5, 6, …, i.e.
anbm= am+tbm: thus, S1  aaaaB | aS1, B bB | .
S2: n m+2, i.e, n+t =m+2, m = n-2 + t for t=0, 1,
2, …, i.e, anbm= anbn-2+t for t=0,1,2, … which
implies anbm= anbn-2 , anbn-1 , anbn , anbn+1 ,
anbn+2 , ....
(anbn-2 :) D  aa K, K aKb | ; (anbn-1:) E
aK; (anbn , anbn+1 , anbn+2 , .... ) F Fb | K; and
S2  D | E | F

20. Examples of showing languages are
Context Free
Show { w: na(w) = nb(w)} is CF.
Show { w: na(w) > nb(w)} is CF.
Show { w: na(w) = 2 nb(w)} is CF.
Try hw # 7 (e) ~ (g) p.133
context free grammar and ambiguity 20

21. S aSb | bSa |SS| (for na = nb)
S1 for na(w) >nb(w) S1 aS1 | aS | SS1
{ w {a,b,c}*: |w|=3na(w)}
E  aEbEc | aEcEb | bEaEc | bEaEc | cEaEb
| cEbEa | EE | (this is for na = nb = nc)
S  aEKEK | KEaEK | KEKEa
K  b | c.
context free grammar and ambiguity 21

22. Derivation Order for w = aab in the CFG:
1. S AB 2. A aaA 4. B Bb
3. A 5. B
Leftmost derivation:
1 2 3 4 5
S AB aaAB aaB aaBb aab
Rightmost derivation:
1 4 5 2 3
S AB ABb Ab aaAb aab
context free grammar and ambiguity 22

23. Derivation Trees
Another way of showing derivation,
independent of the order in which
productions are used.
context free grammar and ambiguity 23

24. S AB A aaA | B Bb |
S AB
S
A B
Every node to its children is corresponding to a
production rule in the grammar
context free grammar and ambiguity 24

25. S AB A aaA | B Bb |
S AB aaAB
S
A B
a a A
context free grammar and ambiguity 25

26. S AB A aaA | B Bb |
S AB aaAB aaABb
S
A B
a a A B b
context free grammar and ambiguity 26

27. S AB A aaA | B Bb |
S AB aaAB aaABb aaBb
S
A B
a a A B b
context free grammar and ambiguity 27

28. S AB A aaA | B Bb |
S AB aaAB aaABb aaBb aab
S
A Derivation
Tree
A B
a a A B b
Every leaf has a
label from T { }
context free grammar and ambiguity 28

29. S AB A aaA | B Bb |
S AB aaAB aaABb aaBb aab
Derivation Tree S
A B
yield
a a A B b aa b
aab
context free grammar and ambiguity 29

30. derivation order doesn’t matter
Leftmost:
S AB aaAB aaB aaBb aab
Rightmost:
S AB ABb Ab aaAb aab
S
Same derivation tree
A B
a a A B b
context free grammar and ambiguity 30

31. S AB A aaA | B Bb |
S Derivation Tree
shows which rules are
A B used in obtaining a w,
but do not give the order
of their applications.
a a A B b
We can find the corresponding
left-most or right-most derivations
from a given derivation tree easily.
context free grammar and ambiguity 31

32. Partial Derivation Trees Every leaf has a label
from T { } V
S AB A aaA | B Bb |
The yield of a partial derivation
S AB tree a sentential form of a
derivation
Partial derivation S
tree with root S
A B
context free grammar and ambiguity 32

33. sentential
S AB aaAB
form
Partial derivation
S
tree with root S
A B
yield
a a A
aaAB
context free grammar and ambiguity 33

34. G: A CFG then Thm. 5.1 on p.132
Every w L(G) there exists a derivation tree
with yield = w. a deriation with the
sentential form w
Conversely,
the yield of any derivation tree w, w L(G)
partial derivation tree tG (with root S), w
Homework for 5.1 (p.133) : 2~5, 7, 8, 11, 13~24
Hand in: 7bef, 8bdg, 13, 15, 17, 18, 21
Prove by induction on the number of steps in the derivation. Check with the
book on p.132.
context free grammar and ambiguity 34

35. Ambiguity
context free grammar and ambiguity 35

36. E E E | E E | (E) | a
a a a
leftmost derivation
E E E E a E a E E
a a E a a*a
E E
a E E
a a
context free grammar and ambiguity 36

37. E E E | E E | (E) | a
a a a leftmost derivation
E E E E E E a E E E
a a E a a a
E E
E E a
a a
context free grammar and ambiguity 37

38. E E E | E E | (E) | a
a a a
Two derivation trees
E E
E E E E
a E E E E a
a a a a
context free grammar and ambiguity 38

39. The grammarE E E | E E | (E) | a
is ambiguous:
Because a string of L(G)
has two derivation trees
E E
a a a
E E E E
a E E E E a
a a a a
context free grammar and ambiguity 39

40. Or we can say
A grammar is ambiguous….
context free grammar and ambiguity 40

41. The grammarE E E | E E | (E) | a
is ambiguous:
There are two different leftmost
derivations for a a a
E E E a E a E E
a a E a a*a
E E E E E E a E E
a a E a a a
context free grammar and ambiguity 41

42. Definition:
A context-free grammar G is ambiguous
if some string w L(G ) has
two or more derivation trees
context free grammar and ambiguity 42

43. In other words:
A context-free grammar G is ambiguous
if some string w L(G ) has:
two or more leftmost derivations
(or rightmost)
context free grammar and ambiguity 43

44. Why do we care about ambiguity?
a a a
take a 2
E E
E E E E
a E E E E a
a a a a
context free grammar and ambiguity 44

45. 2 2 2
E E
E E E E
2 E E E E 2
2 2 2 2
context free grammar and ambiguity 45

46. 2 2 2 6 2 2 2 8
6 8
E E
2 4 4 2
E E E E
2 2 2 2
2 E E E E 2
2 2 2 2
context free grammar and ambiguity 46

47. Correct result: 2 2 2 6
6
E
2 4
E E
2 2
2 E E
2 2
context free grammar and ambiguity 47

48. • Ambiguity is bad for programming languages
• We want to remove ambiguity
context free grammar and ambiguity 48

49. We fix the ambiguous grammar:
E E E | E E | (E) | a
New non-ambiguous grammar: E E T
E T
T T F
T F
F (E)
context free grammar and ambiguity F a 49

50. E E T T T F T a T a T F
a F F a a F a a a
E a a a
E E T
E T
E T
T T F T T F
T F
F F a
F (E)
F a a a
context free grammar and ambiguity 50

51. Unique derivation tree
E a a a
E T
T T F
F F a
a a
context free grammar and ambiguity 51

52. The grammar G: E E T
E T
T T F
T F
F (E)
F a
is non-ambiguous:
i.e. EVERY stringw L (G ) has
a unique derivation tree
context free grammar and ambiguity 52

53. Inherent Ambiguity
Some context free languages
have only ambiguous grammars
Example: n n m n m m
L {a b c } {a b c }
S S1 | S2 S1 S1c | A S2 aS2 | B
A aAb | B bBc |
context free grammar and ambiguity 53

54. n n n
The string a b c
has two derivation trees
S S
S1 S2
S1 c a S2
context free grammar and ambiguity 54

55. Compilers
context free grammar and ambiguity 55

56. Machine Code
Program Add v,v,0
v = 5; cmp v,5
if (v>5) jmplt ELSE
x = 12 + v; THEN:
while (x !=3) { Compiler
add x, 12,v
x = x - 3; ELSE:
v = 10; WHILE:
} cmp x,3
...... ...
context free grammar and ambiguity 56

57. A parser knows the grammar
of the programming language
Lexical
Compiler parser
analyzer
input output
machine
program
Lexical analyzer : analyze the given input code
is composed of (identifier, or an expression, 57
or a statement, etc)
context free grammar and ambiguity

58. Parser
PROGRAM STMT_LIST
STMT_LIST STMT; STMT_LIST | STMT;
STMT EXPR | IF_STMT | WHILE_STMT
| { STMT_LIST }
EXPR EXPR + EXPR | EXPR - EXPR | ID
IF_STMT if (EXPR) then STMT
| if (EXPR) then STMT else STMT
WHILE_STMT while (EXPR) do STMT
context free grammar and ambiguity 58

59. The parser finds the derivation
of a particular input
derivation
Parser
input E => E + E
E -> E + E
=> E + E * E
10 + 2 * 5 |E*E
=> 10 + E*E
| INT
=> 10 + 2 * E
=> 10 + 2 * 5
context free grammar and ambiguity 59

60. derivation tree
derivation
E
E => E + E E + E
=> E + E * E
=> 10 + E*E 10
E * E
=> 10 + 2 * E
=> 10 + 2 * 5 2 5
context free grammar and ambiguity 60

61. derivation tree
E machine code
E + E mult a, 2, 5
add b, 10, a
10
E * E
2 5
context free grammar and ambiguity 61

62. Parsing
context free grammar and ambiguity 62

63. Parser
input
grammar derivation
string
context free grammar and ambiguity 63

64. Example:
Parser
S SS derivation
input
S aSb
aabb ?
S bSa
S
context free grammar and ambiguity 64

65. Exhaustive Search
S SS | aSb | bSa |
Phase 1: S SS Find derivation of
S aSb aabb
S bSa
S
All possible derivations of length 1
context free grammar and ambiguity 65

66. S SS aabb
S aSb
S bSa
S
context free grammar and ambiguity 66

67. Phase 2 S SS | aSb | bSa |
S SS SSS
S SS aSbS aabb
Phase 1 S SS bSaS
S SS S SS S
S aSb S aSb aSSb
S aSb aaSbb
S aSb abSab
S aSb ab
context free grammar and ambiguity 67

68. Phase 2 S SS | aSb | bSa |
S SS SSS
S SS aSbS aabb
S SS S
S aSb aSSb
S aSb aaSbb
Phase 3
S aSb aaSbb aabb
context free grammar and ambiguity 68

69. Final result of exhaustive search
(top-down parsing)
Parser
S SS
input
S aSb
aabb
S bSa
S
What happen if derivation
there is no such
derivation existed?
I.e. what if w L(G)? S aSb aaSbb aabb
context free grammar and ambiguity 69

70. Is this searching method an
algorithm?
What if w L(G)?
context free grammar and ambiguity 70

71. Time complexity of exhaustive search
Suppose there are no productions of the form
A : - production
A B : unit - production
Number of phases for string w : 2| w|
So that after the execution of every phase, either
(1) the sentential form has additional one or more
terminal symbols; and/or
(2) the length of the sentential form is increased by at
least one.
context free grammar and ambiguity 71

72. For grammar with k rules
Time for phase 1: k
k possible derivations
context free grammar and ambiguity 72

73. Time for phase 2: k 2
k 2 possible derivations
context free grammar and ambiguity 73

74. Time for phase 2 | w |: k 2|w|
2|w| possible derivations
k
context free grammar and ambiguity 74

75. Total time needed for string w:
2 2|w|
k k  k
phase 1 phase 2 phase 2|w|
Extremely bad!!!
context free grammar and ambiguity 75

76. There exist faster algorithms
for specialized grammars
Simple grammar: A ax
ONE symbol V*: string
from of variables
such that pair ( A, a ) appears at most once
context free grammar and ambiguity 76

77. S aS
S-grammar example:
S bSS
S c
Not an S-grammar: S aS
S bSS | bS
S
context free grammar and ambiguity 77

78. Simple grammar: A ax
Observe that if G is an S-grammar, then
G has no productions like
A : - production
A B : unit - production
In a derivation process for S-grammar, every
phase will increase one terminal symbol.
context free grammar and ambiguity 78

79. S aS
S-grammar example:
S bSS
S c
Find a (left most)derivation for abcc:
S aS abSS abcS abcc
Find a (left most)derivation for bca:
S bSS bcS bcaS
bca L(G) since |bcaS| > | bca |
context free grammar and ambiguity 79

80. If G is an S-grammar, then
in the exhaustive search parsing
there is only one choice in each phase
Thus, for any given string w, it
takes a linear time, O(|w|), to decide
either w L(G) by providing a
unique derivation or w L(G).
Not every CF grammar can be converted into an S-grammar.
context free grammar and ambiguity 80

81. S-grammar Example
Let G = (V, T, S, P) be an S-grammar:
Give an expression for the maximum
size of P in terms of |V| and |T|.
Is it possible for an s-grammar to be
ambiguous?
context free grammar and ambiguity 81

82. For GENERAL context-free grammars:
There exists a parsing algorithm
that parses a string w
in time | w |3
The CYK membership algorithm (on 6.3)
5.2 HW p.144
1~9,11~15,17~19
context free grammar and ambiguity 82