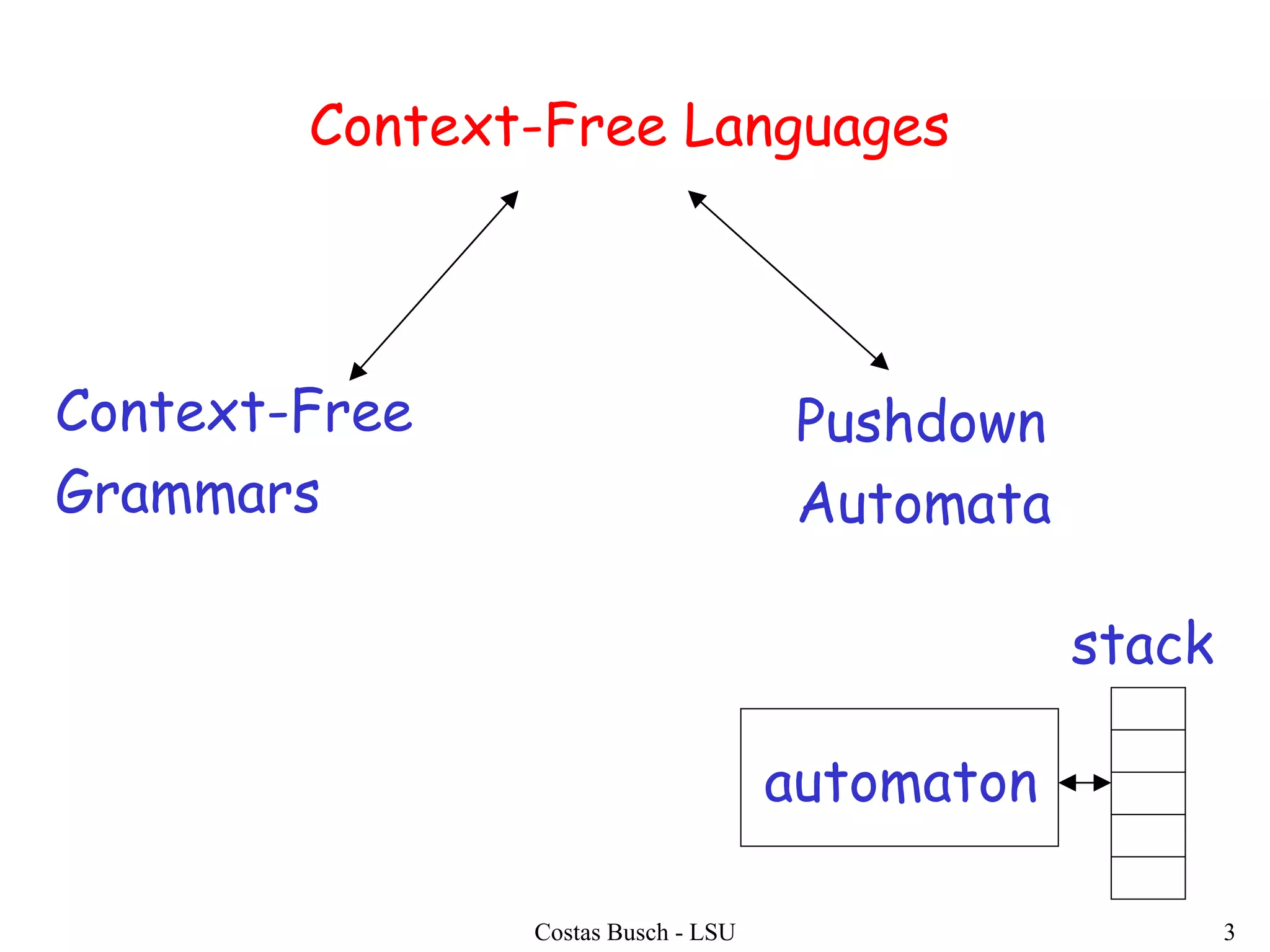
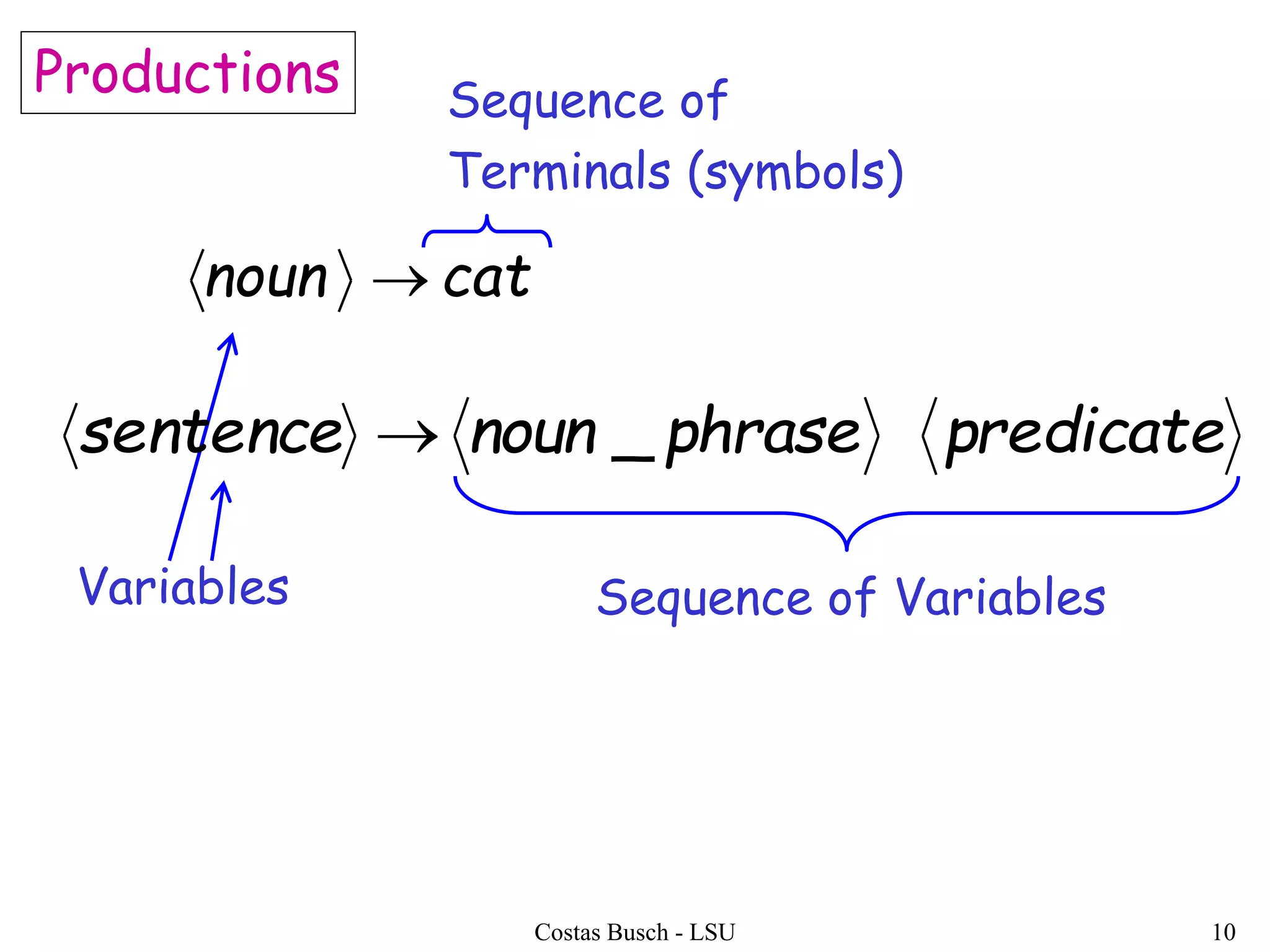
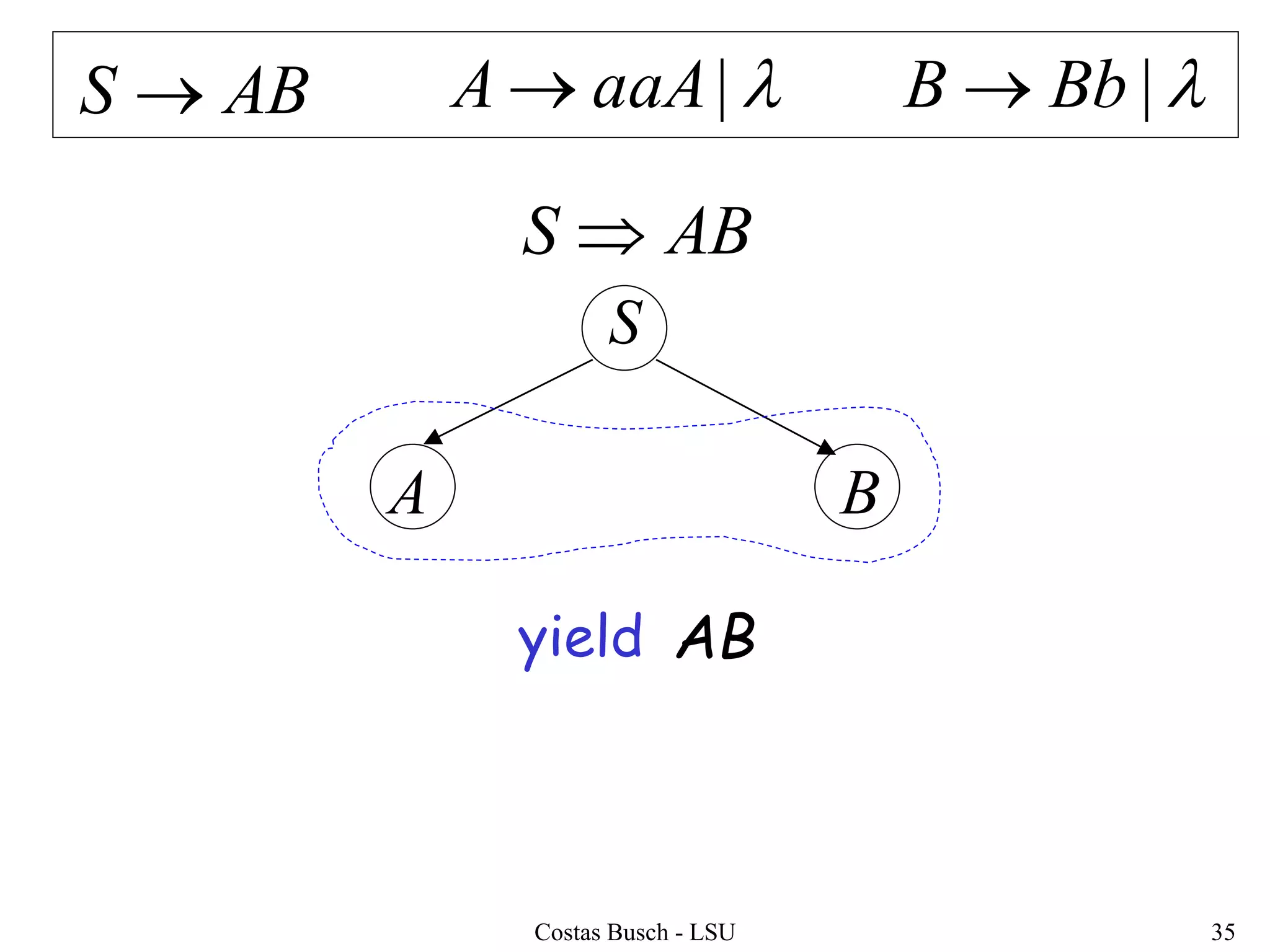
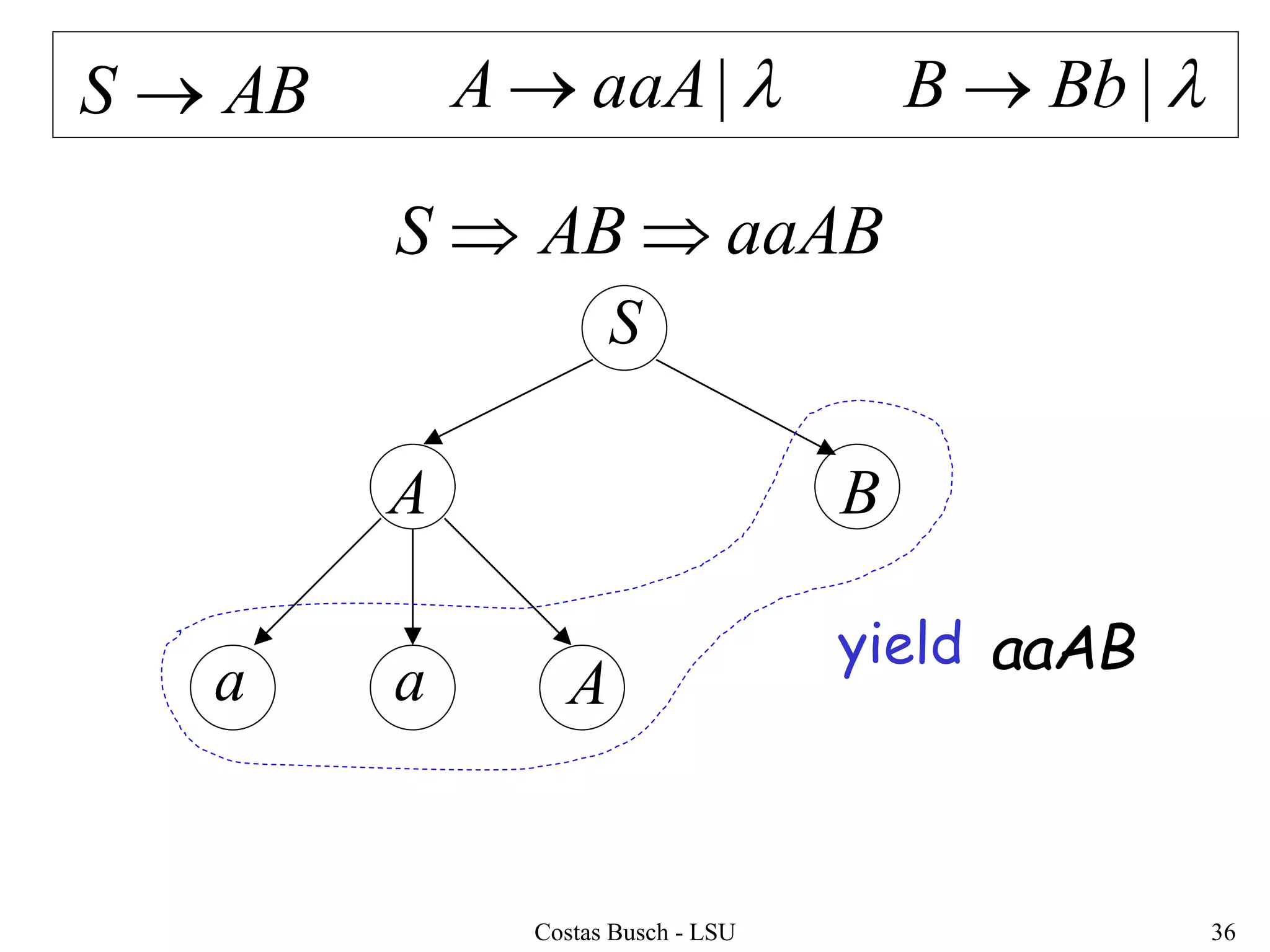
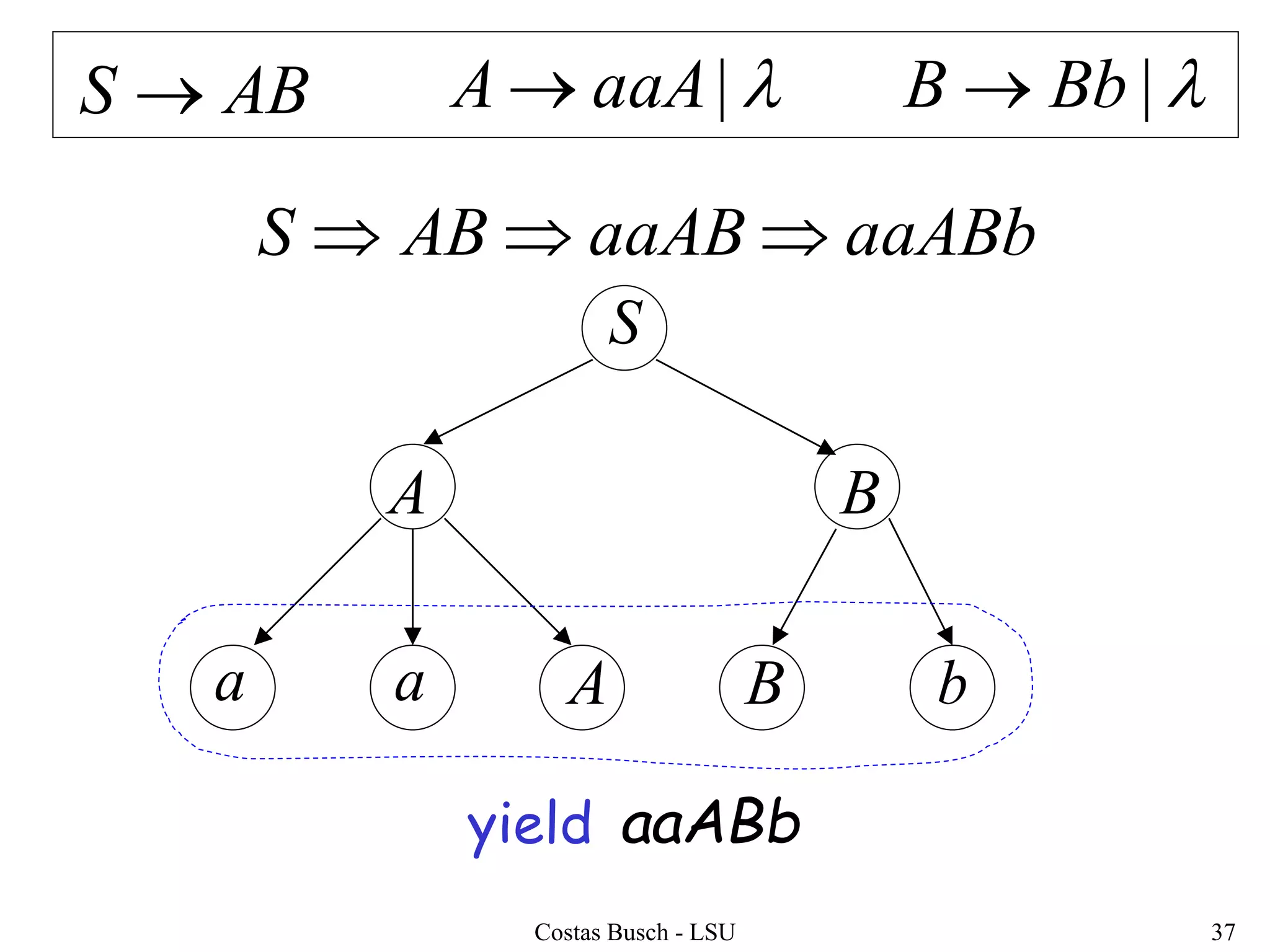
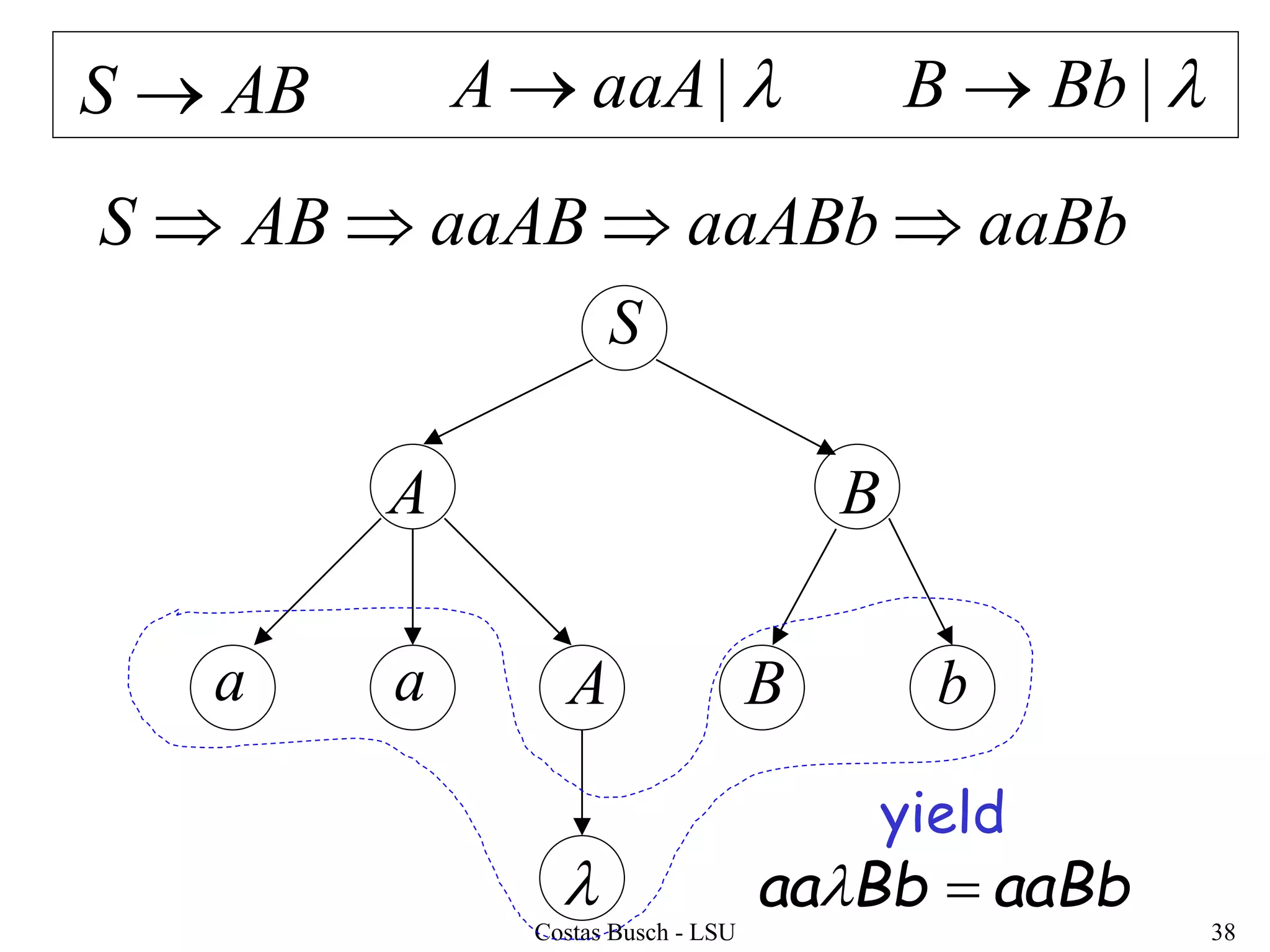
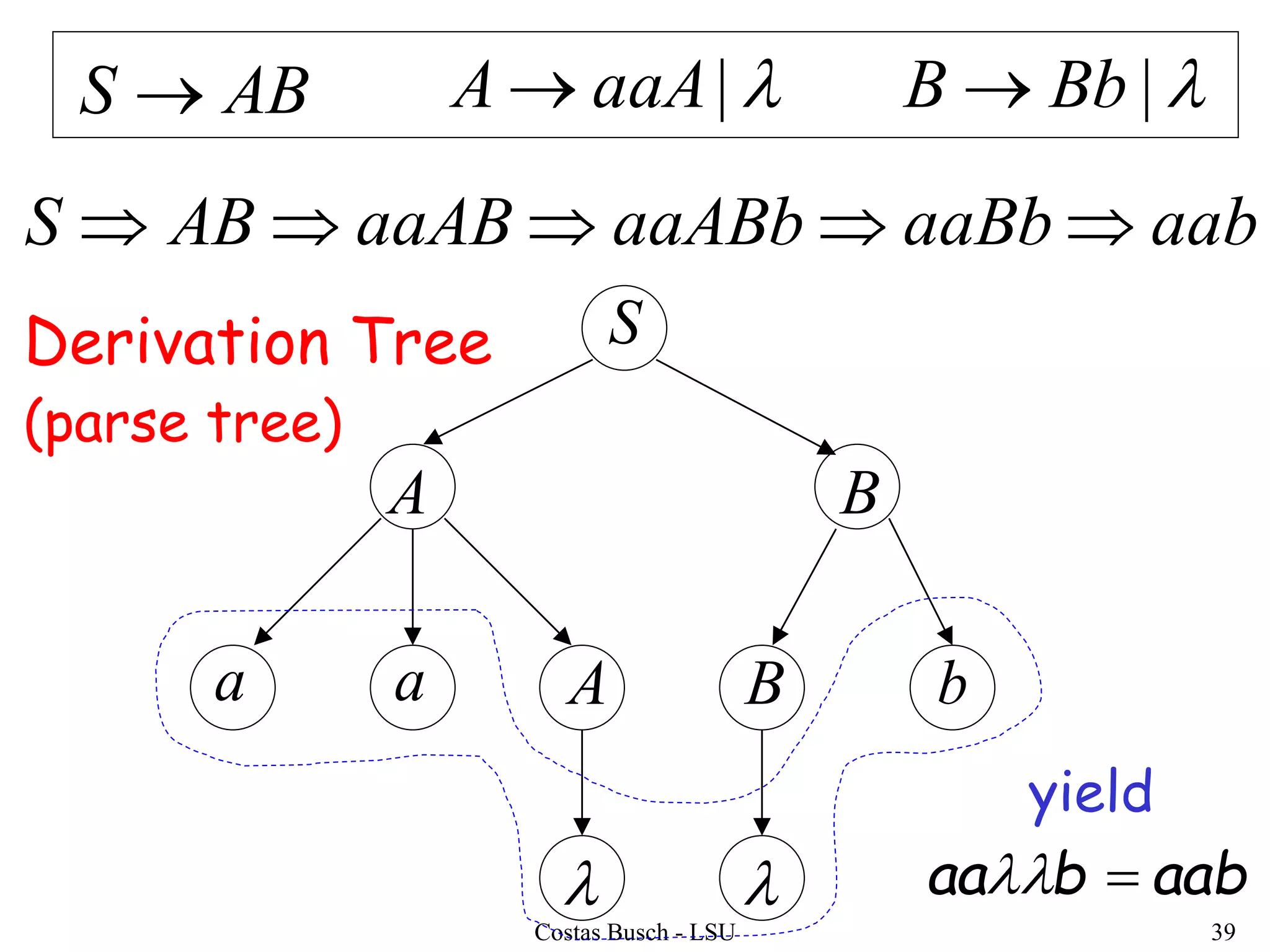
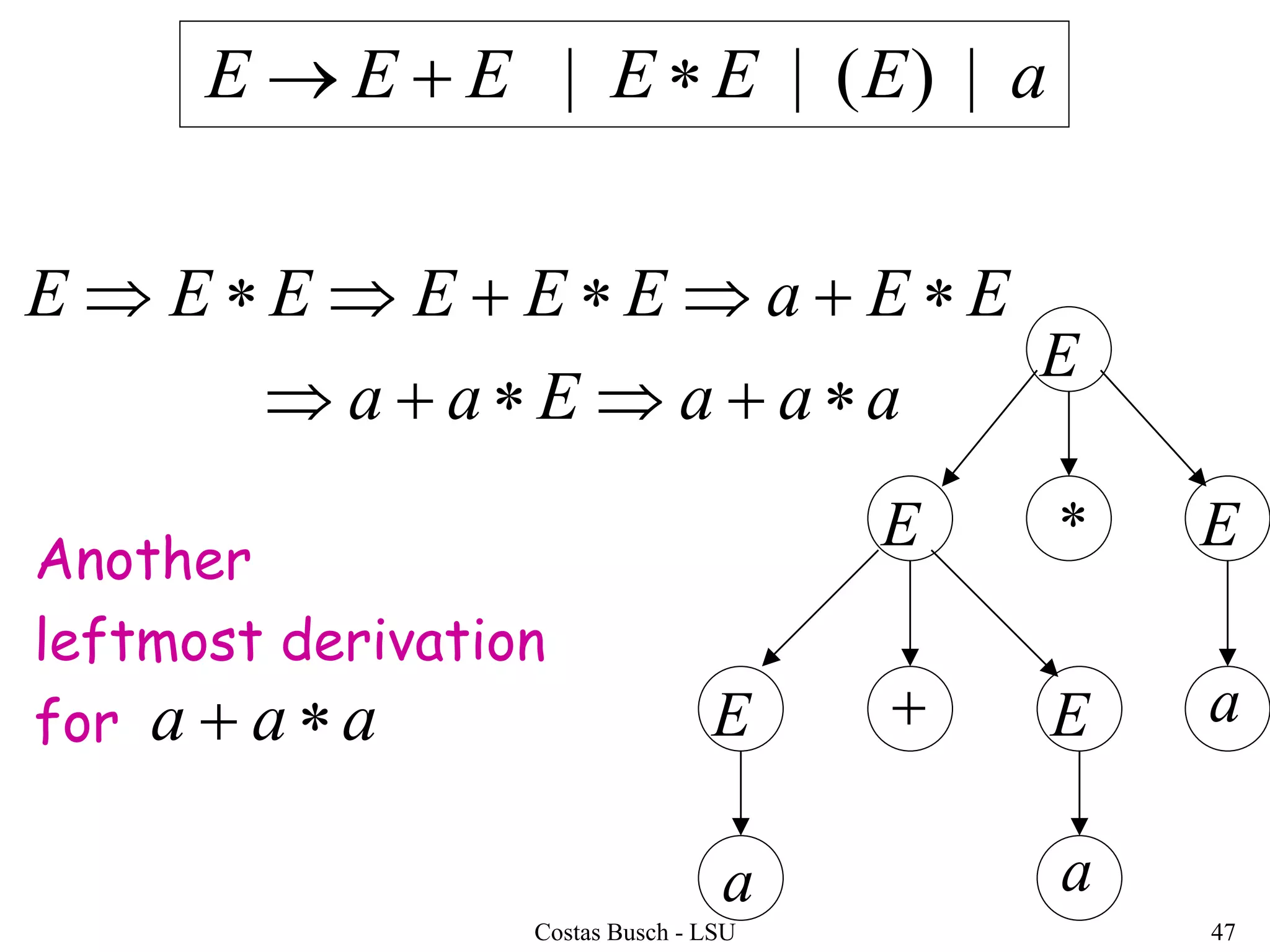
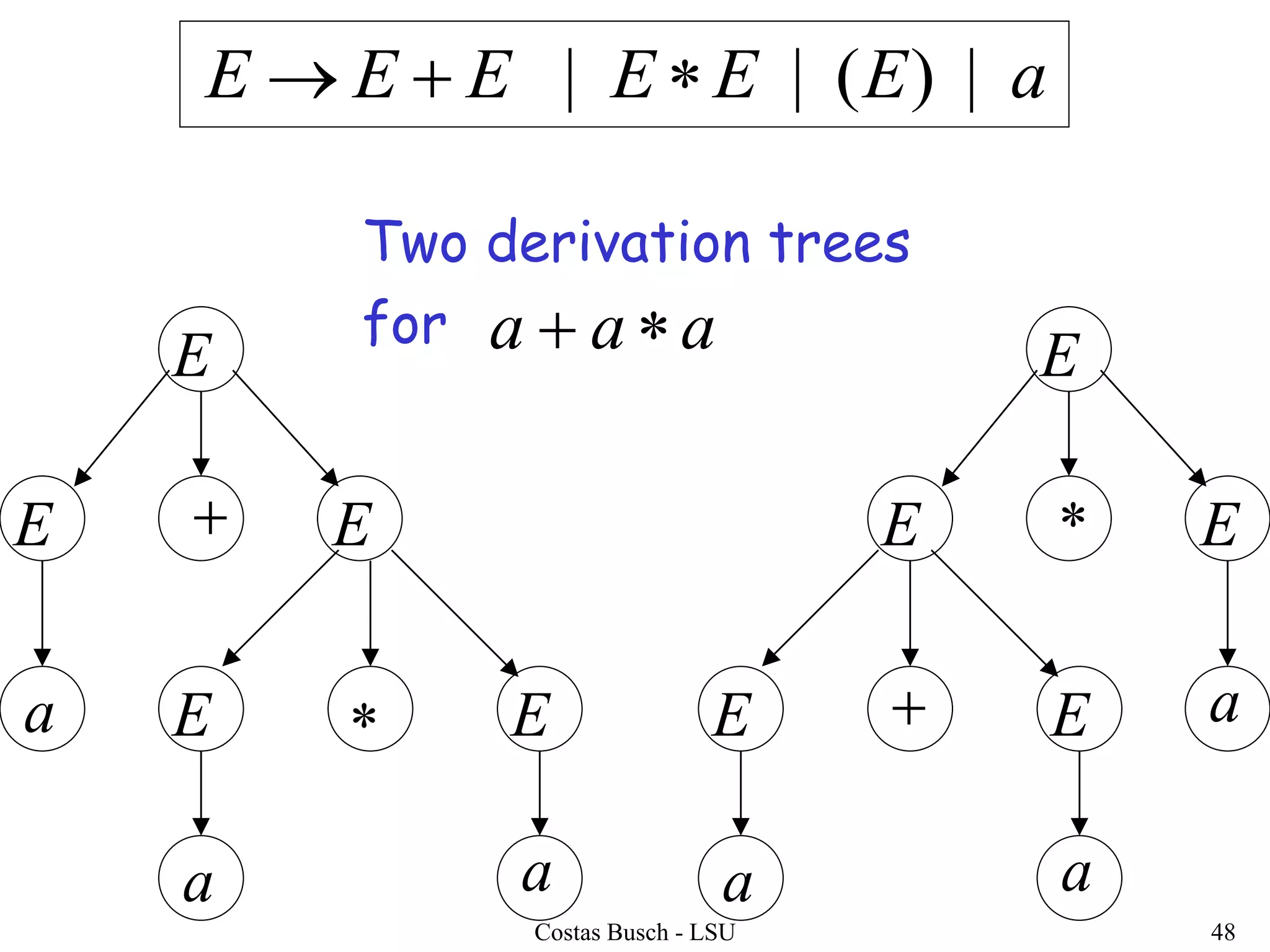
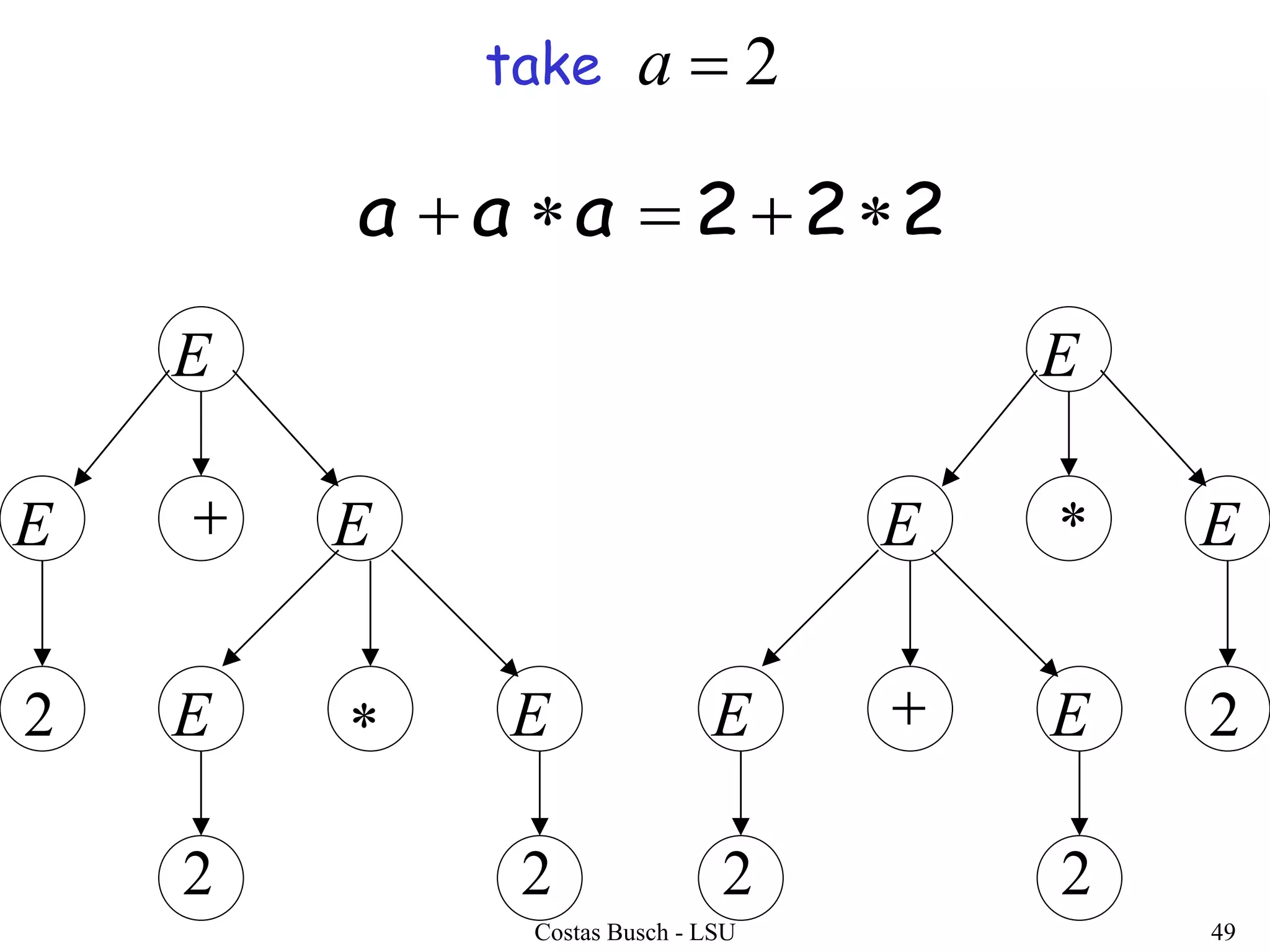
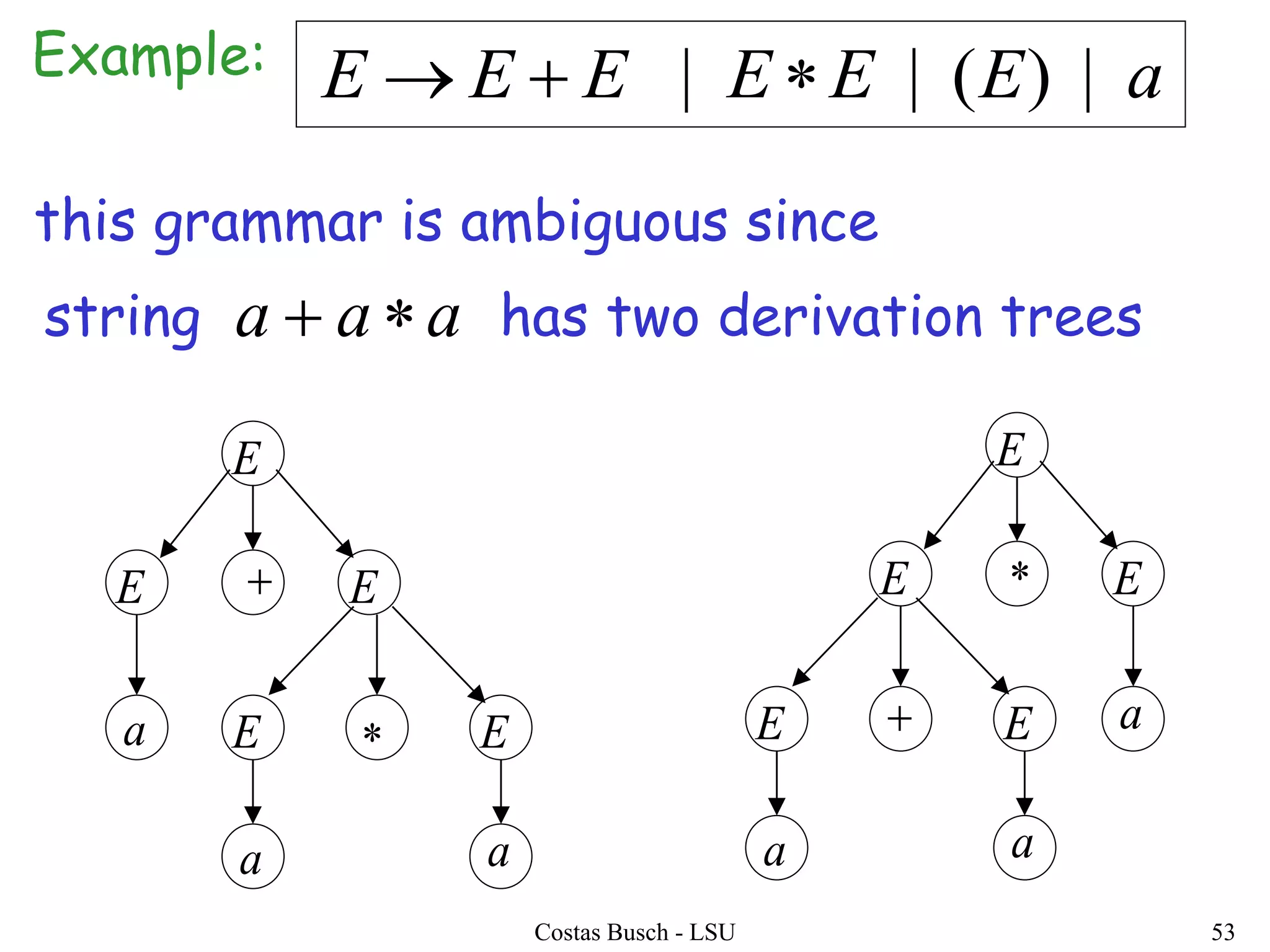
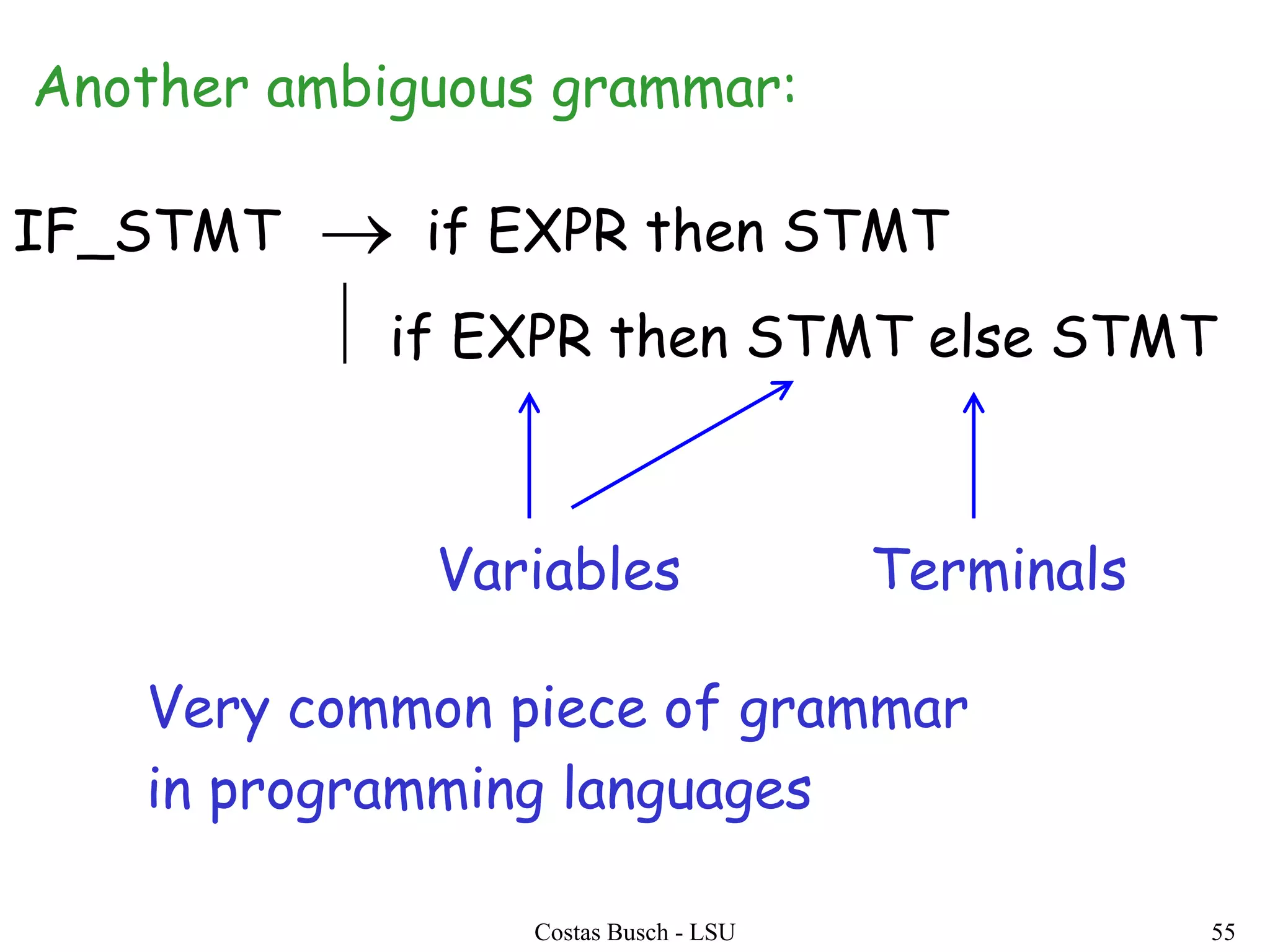
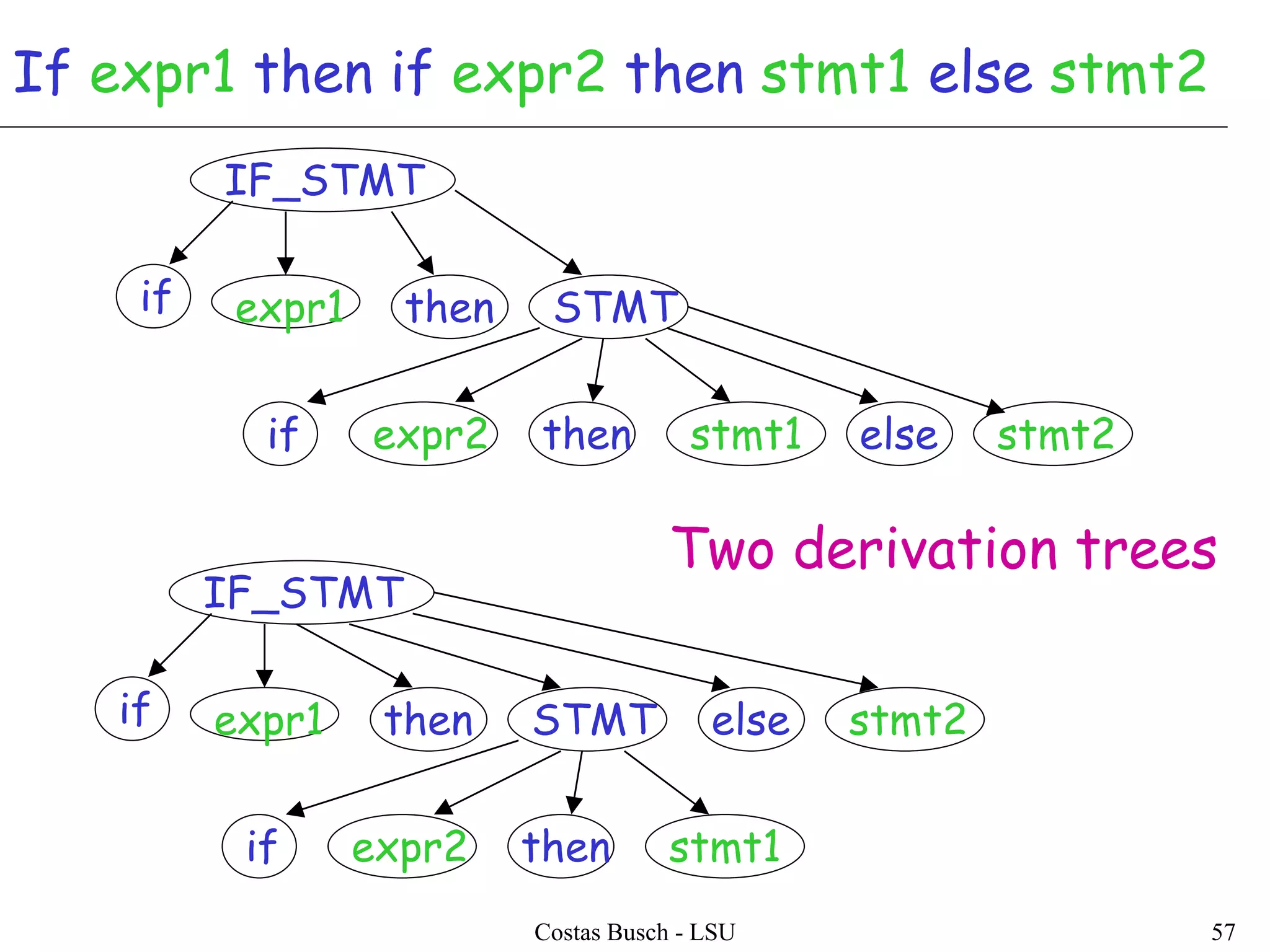
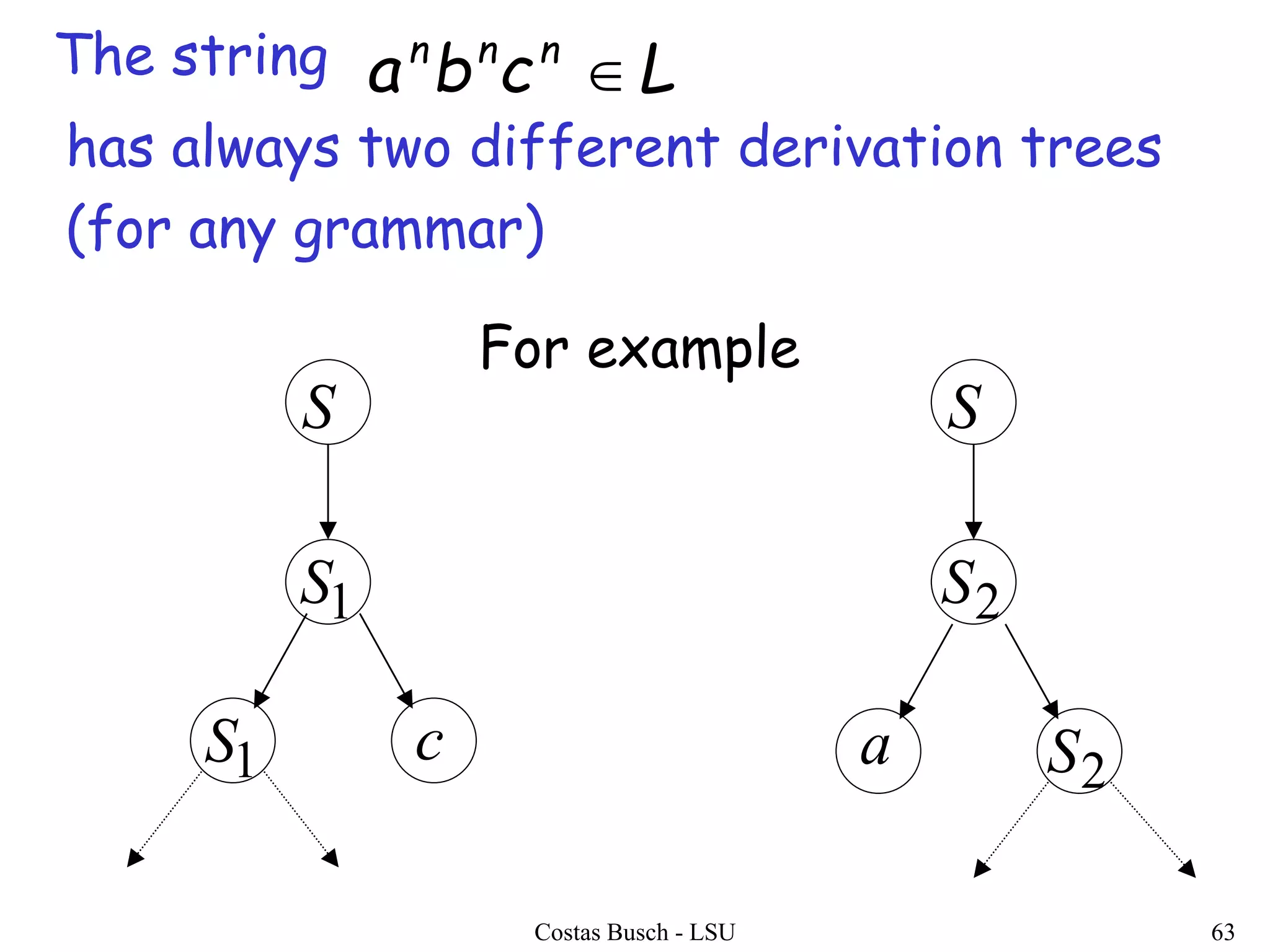
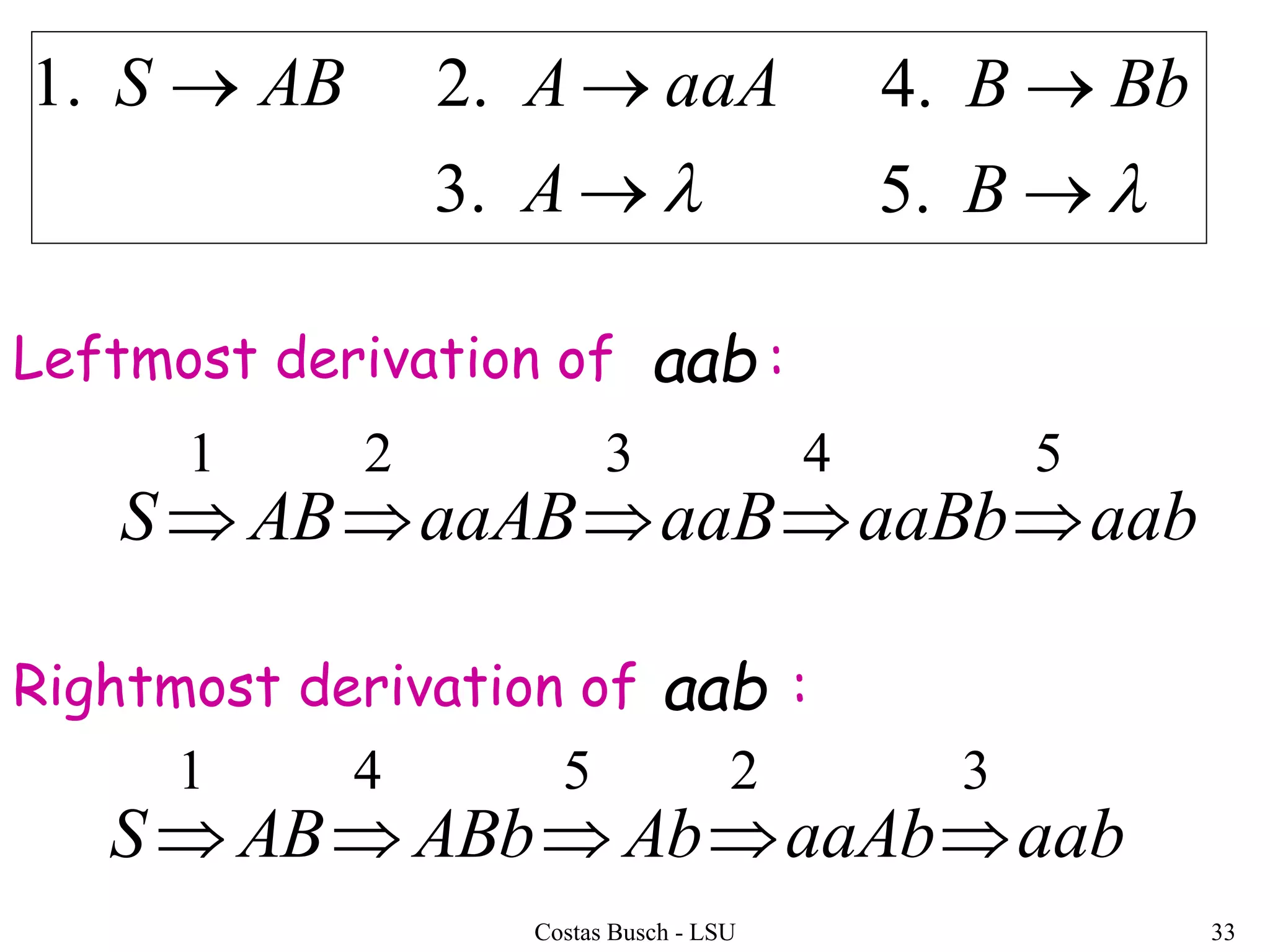The document discusses context-free grammars and ambiguity in context-free grammars. It provides examples of context-free grammars that generate languages like strings of matching parentheses. It describes derivation trees and shows that an expression grammar is ambiguous because the string "aaa * +" can have two different derivation trees, leading to different evaluations of the expression. The document defines that a context-free grammar is ambiguous if a string has two different derivation trees or leftmost derivations.

1. Costas Busch - LSU 1
Context-Free Languages

2. Costas Busch - LSU 2
Regular Languages
}0:{ nba nn }{ R
ww
**ba *)( ba 
Context-Free Languages

3. Costas Busch - LSU 3
Context-Free Languages
Pushdown
Automata
Context-Free
Grammars
stack
automaton

4. Costas Busch - LSU 4
Context-Free Grammars

5. Costas Busch - LSU 5
Grammars
Grammars express languages
Example: the English language grammar
verbpredicate
nounarticlephrasenoun
predicatephrasenounsentence



_
_

6. Costas Busch - LSU 6
sleepsverb
runsverb
dognoun
catnoun
thearticle
aarticle







7. Costas Busch - LSU 7
Derivation of string “the dog sleeps”:
sleepsdogthe
verbdogthe
verbnounthe
verbnounarticle
verbphrasenoun
predicatephrasenounsentence






_
_

8. Costas Busch - LSU 8
Derivation of string “a cat runs”:
runscata
verbcata
verbnouna
verbnounarticle
verbphrasenoun
predicatephrasenounsentence






_
_

9. Costas Busch - LSU 9
Language of the grammar:
L = { “a cat runs”,
“a cat sleeps”,
“the cat runs”,
“the cat sleeps”,
“a dog runs”,
“a dog sleeps”,
“the dog runs”,
“the dog sleeps” }

10. Costas Busch - LSU 10
catnoun 
Variables
Sequence of
Terminals (symbols)
Productions
predicatephrasenounsentence _
Sequence of Variables

11. Costas Busch - LSU 11
Another Example


S
aSbSGrammar:
Variable
Sequence of
terminals and variables
The right side
may be 

12. Costas Busch - LSU 12
Grammar:
Derivation of string :


S
aSbS
abaSbS 
ab
aSbS  S

13. Costas Busch - LSU 13
Grammar:
Derivation of string :
aabbaaSbbaSbS 
aSbS  S
aabb


S
aSbS

14. Costas Busch - LSU 14
aaabbbaaaSbbbaaSbbaSbS 
aaaabbbbaaaaSbbbb
aaaSbbbaaSbbaSbS


Other derivations:


S
aSbSGrammar:

15. Costas Busch - LSU 15


S
aSbS
}0:{  nbaL nn
Grammar:
Language of the grammar


16. Costas Busch - LSU 16
We write:
Instead of:
aaabbbS
*

aaabbbaaaSbbbaaSbbaSbS 
for zero or more derivation steps
A Convenient Notation

17. Costas Busch - LSU 17
nww
*
1 
nwwww  321
in zero or more derivation steps
In general we write:
If:
ww
*
Trivially:

18. Costas Busch - LSU 18


S
aSbS
aaabbbS
abS
S
*
*
*



Example Grammar Possible Derivations
baaaaaSbbbbaaSbbS



19. Costas Busch - LSU 19


S
aSbS
|aSbS 
thearticle
aarticle


theaarticle |
Another convenient notation:

20. Costas Busch - LSU 20
Formal Definitions
 PSTVG ,,,
Set of
variables
Set of
terminal
symbols
Start
variable
Set of
productions
Grammar:

21. Costas Busch - LSU 21
Context-Free Grammar:
All productions in are of the form
sA 
String of
variables and
terminals
),,,( PSTVG 
P
Variable

22. Costas Busch - LSU 22
|aSbS 
 PSTVG ,,,
}{SV 
},{ baT 
},{  SaSbSP
variables
terminals
productions
start variable
Example of Context-Free Grammar

23. Costas Busch - LSU 23
For a grammar with start variableG S
String of terminals or
*},:{)(
*
TwwSwGL 

Language of a Grammar:

24. Costas Busch - LSU 24
context-free grammar :
}0:{)(  nbaGL nn
nn
baS


G
Example:
Since, there is derivation
for any 0n
|aSbS 

25. Costas Busch - LSU 25
A language is context-free
if there is a context-free grammar
with
L
G
)(GLL 
Context-Free Language definition:

26. Costas Busch - LSU 26
since context-free grammar :
}0:{  nbaL nn
G
Example:
is a context-free language
generates LGL )(
|aSbS 

27. Costas Busch - LSU 27
||bSbaSaS 
abbaabSbaaSaS 
Context-free grammar :G
Example derivations:
abaabaabaSabaabSbaaSaS 
)(GL }*},{:{ bawwwR

Palindromes of even length
Another Example

28. Costas Busch - LSU 28
|| SSaSbS 
ababSaSbSSSS 
Context-free grammar :G
Example derivations:
abababaSbabSaSbSSSS 
}prefixanyin
)()(and
),()(:{
v
vnvn
wnwnw
ba
ba

)(GL
() ((( ))) (( ))
Describes
matched
parentheses: )b(, a
Another Example

29. Costas Busch - LSU 29
Derivation Order
and
Derivation Trees

30. Costas Busch - LSU 30
Derivation Order
Consider the following example grammar
with 5 productions:
ABS .1


A
aaAA
.3
.2


B
BbB
.5
.4

31. Costas Busch - LSU 31
aabaaBbaaBaaABABS
54321

Leftmost derivation order of string aab :
At each step, we substitute the
leftmost variable
ABS .1


A
aaAA
.3
.2


B
BbB
.5
.4
Derivation of aab

32. Costas Busch - LSU 32
aabaaAbAbABbABS
32541

Rightmost derivation order of string aab:
At each step, we substitute the
rightmost variable
ABS .1


A
aaAA
.3
.2


B
BbB
.5
.4
Derivation of aab

33. Costas Busch - LSU 33
aabaaAbAbABbABS
32541

Rightmost derivation of :aab
aabaaBbaaBaaABABS
54321

Leftmost derivation of :aab
ABS .1


A
aaAA
.3
.2


B
BbB
.5
.4

34. Costas Busch - LSU 34
Derivation Trees
Consider the same example grammar:
aabaaBbaaABbaaABABS 
And a derivation of :aab
ABS  |aaAA  |BbB 

35. Costas Busch - LSU 35
ABS 
S
BA
ABS  |aaAA  |BbB 
yield AB

36. Costas Busch - LSU 36
aaABABS 
a a A
S
BA
ABS  |aaAA  |BbB 
yield aaAB

37. Costas Busch - LSU 37
aaABbaaABABS 
S
BA
a a A B b
ABS  |aaAA  |BbB 
yield aaABb

38. Costas Busch - LSU 38
aaBbaaABbaaABABS 
S
BA
a a A B b

ABS  |aaAA  |BbB 
yield
aaBbBbaa 

39. Costas Busch - LSU 39
aabaaBbaaABbaaABABS 
yield
aabbaa 
S
BA
a a A B b
 
Derivation Tree
ABS  |aaAA  |BbB 
(parse tree)

40. Costas Busch - LSU 40
aabaaBbaaBaaABABS 
aabaaAbAbABbABS 
TRY IT OUT!
Sometimes, derivation order doesn’t matter
Leftmost derivation:
Rightmost derivation:

41. Costas Busch - LSU 41
aabaaBbaaBaaABABS 
aabaaAbAbABbABS 
S
BA
a a A B b
 
Give same
derivation tree
Sometimes, derivation order doesn’t matter
Leftmost derivation:
Rightmost derivation:

42. Costas Busch - LSU 42
Ambiguity

43. Costas Busch - LSU 43
Grammar for mathematical expressions
))(()( aaaaaaa 
Example strings:
Denotes any number
aEEEEEE |)(|| 

44. Costas Busch - LSU 44
A leftmost derivation
for aaa 
aaaEaa
EEaEaEEE
*

aEEEEEE |)(|| 
PARSE TREE ???

45. Costas Busch - LSU 45
A leftmost derivation
for aaa 
E
EE
EE

a
a a

aaaEaa
EEaEaEEE
*

aEEEEEE |)(|| 

46. Costas Busch - LSU 46
aaaEaa
EEaEEEEEE


Another
leftmost derivation
for
aEEEEEE |)(|| 
aaa 
PARSE TREE ???

47. Costas Busch - LSU 47
E
EE

a a

EE a
aaaEaa
EEaEEEEEE


Another
leftmost derivation
for
aEEEEEE |)(|| 
aaa 

48. Costas Busch - LSU 48
aaa  E
EE

a a

EE a
E
EE
EE

a
a a

Two derivation trees
for
aEEEEEE |)(|| 

49. Costas Busch - LSU 49
E
EE


EE
E
EE
EE

2
2 2 2 2
2
222  aaa
take 2a

50. Costas Busch - LSU 50
E
EE


EE
E
EE
EE


6222 
2
2 2 2 2
2
8222 
4
2 2
2
6
2 2
24
8
Good Tree Bad Tree
Compute expression result
using the tree

51. Costas Busch - LSU 51
Two different derivation trees
may cause problems in applications which
use the derivation trees:
• Evaluating expressions
• In general, in compilers
for programming languages

52. Costas Busch - LSU 52
Ambiguous Grammar:
A context-free grammar is ambiguous
if there is a string which has:
two different derivation trees
or
two leftmost derivations
G
)(GLw
(Two different derivation trees give two
different leftmost derivations and vice-versa)

53. Costas Busch - LSU 53
E
EE

a a

EE a
E
EE
EE

a
a a

string aaa  has two derivation trees
aEEEEEE |)(|| 
this grammar is ambiguous since
Example:

54. Costas Busch - LSU 54
string aaa  has two leftmost derivations
aaaEaa
EEaEEEEEE


aaaEaa
EEaEaEEE
*

aEEEEEE |)(|| 
this grammar is ambiguous also because

55. Costas Busch - LSU 55
IF_STMT if EXPR then STMT
| if EXPR then STMT else STMT
Another ambiguous grammar:
Variables Terminals
Very common piece of grammar
in programming languages

56. Costas Busch - LSU 56
If expr1 then if expr2 then stmt1 else stmt2
TWO
Parse Trees
or
Derivation Trees
???

57. Costas Busch - LSU 57
If expr1 then if expr2 then stmt1 else stmt2
IF_STMT
expr1 then
elseif expr2 then
STMT
stmt1
if
IF_STMT
expr1 then else
if expr2 then
STMT stmt2if
stmt1
stmt2
Two derivation trees

58. Costas Busch - LSU 58
In general, ambiguity is bad
and we want to remove it
Sometimes it is possible to find
a non-ambiguous grammar for a language
But, in general ιt is difficult to achieve this

59. Costas Busch - LSU 59
aE
EE
EEE
EEE




)(
aEF
FFTT
TTEE
|)(
|
|



Ambiguous
Grammar
Non-Ambiguous
Grammar
Equivalent
generates the same
language
A successful example:

60. Costas Busch - LSU 60
aaaFaaFFa
FTaTaTFTTTEE


E
E T
T  F
F
a
T
F
a
a
aEF
FFTT
TTEE
|)(
|
|



Unique
derivation tree
for aaa 

61. Costas Busch - LSU 61
}{}{ mmnmnn
cbacbaL 
0, mn
An un-successful example:
every grammar that generates this
language is ambiguous
L is inherently ambiguous:

62. Costas Busch - LSU 62
}{}{ mmnmnn
cbacbaL 
|
|11
aAbA
AcSS


|
|22
bBcB
BaSS

21 | SSS 
Example (ambiguous) grammar for :L

63. Costas Busch - LSU 63
The string Lcba nnn

has always two different derivation trees
(for any grammar)
S
1S
S
2S
1S c 2Sa
For example