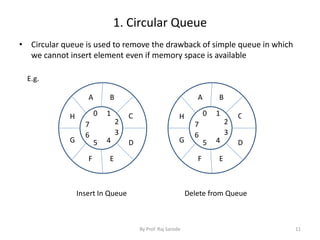
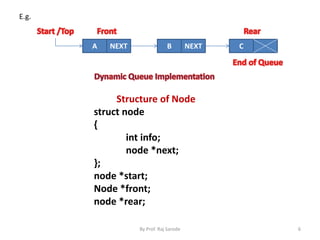
Queue is a linear data structure where elements are inserted at one end called the rear and deleted from the other end called the front. It follows the FIFO (first in, first out) principle. Queues can be implemented using arrays or linked lists. In an array implementation, elements are inserted at the rear and deleted from the front. In a linked list implementation, nodes are added to the rear and removed from the front using front and rear pointers. There are different types of queues including circular queues, double-ended queues, and priority queues.

1. Chapter 5
Queue

2. Queue
“Queue is a linear data structure in which elements can
be inserted from one end (called the Rear end) &
Deleted from the other end (called the Front end)”
FIFO – First in First Out Or
First come First Server
e.g. People standing in Queue
for Movie Ticket
By Prof. Raj Sarode 2
In Computer Science
 Scheduling Algorithm
 Process Management

3. Implementation or Representation of Queue
1 Static / sequential / array representation
 In this case of array, Queue is also collection of
homogeneous elements .
 Therefore Queue can be easily implemented
using array.
 Two operation : Insert & Delete
 Front =-1 or NULL shows queue is empty
 Queue is usually grows at rear & shrinks from
the front end
By Prof. Raj Sarode 3

4. Front=1
Front=2
Front=3
By Prof. Raj Sarode 4
Front=-1
0 1 2 3 4
Rear=-1
Front=0
A
0 1 2 3 4
Rear=0
1
2
Insert A
Front=0
A B
0 1 2 3 4
Rear=1
3
Insert B
Front=0
A B C
0 1 2 3 4
Rear=2
4
Insert C
B C
0 1 2 3 4
Rear=2
5
Delete
C
0 1 2 3 4
Rear=2
6
Delete
0 1 2 3 4
Rear=2
7
Delete
Queue is empty
Queue is empty
Entry point is called Rear &
Exit point is called Front

5. 2 Dynamic / pointer/ linked Representation
 In Dynamic or linked representation Queue is
collection of nodes. Where each node is divided in to
two parts
INFO NEXT
 In linked representation, queue is implemented as a
linked list with two pointer variables Front & Rear
Pointer Front= NULL - Queue is Empty
Rear->Next = NULL - Last node of Queue of End of
Queue
By Prof. Raj Sarode 5
Store Data <-
Structure of Node
->Point to next Node

6. A NEXT B NEXT C
E.g.
Structure of Node
struct node
{
int info;
node *next;
};
node *start;
Node *front;
node *rear;
By Prof. Raj Sarode 6

7. Queue Operation
1. Insert in the Queue ( Enqueue )
Enqueue ; inserts an element at the rear of
the queue
2. Delete from Queue ( Dequeue )
Dequeue ; deletes an element at the front of
the queue.
By Prof. Raj Sarode 7

8. Algorithm 1
Q insert (Queue, MAX, FRONT, REAR, Element)
1. Check for Overflow
a. If REAR=MAX-1
or
FRONT = REAR+1 then
b. Print “overflow” & return
2. If FRONT =-1 then
Set FRONT=REAR=0
else if REAR=MAX then
Set REAR=FRONT=0
else Set REAR=REAR+1 //Increment Rear by 1
End if
End if
3. QUEUE [REAR] = Element //Insert the Element at New Location
4. Return.
By Prof. Raj Sarode 8

9. Algorithm 2
Q delete (Queue, MAX, FRONT, REAR, Element)
1. Check for Underflow
a. If FRONT=-1 then
b. Print “underflow” & return
Else
2. Element= Queue[FRONT] //delete element from queue
3. If FRONT=REAR then
Set FRONT=REAR=-1
Else
FRONT=FRONT+1 //Increment the Front by one
End if
4. Return
By Prof. Raj Sarode 9

10. Types Of Queue
1. Circular Queue
2. Deque (Double Ended Queue)
3. Priority Queue
By Prof. Raj Sarode 10

11. 1. Circular Queue
• Circular queue is used to remove the drawback of simple queue in which
we cannot insert element even if memory space is available
I J
7 7
3
By Prof. Raj Sarode 11
3
H
B
C
D
F E
G
A
E.g.
0 1
2
3
5 4
6
H
B
C
D
F E
G
A
0 1
2
3
5 4
6
K
Insert In Queue Delete from Queue

12. 2. Deque (Double Ended Queue)
• Deque is double ended queue in which insertion and deletion
can be performed from both ends, Rear and Front
• It follows same strategy as simple queue .
A B C D E
0 1 2 3 4 5 6 7 8
EA FB C D E
0 1 2 3 4 5 6 7 8
By Prof. Raj Sarode 12

13. 2. Priority Queue
• Is a special queue in which insertion and deletion of elements are
performed according to priority assigned to them.
• It does not follow FIFO principle as in other queue.
• The elements of highest priority are proceed first than lowest
priority elements.
• Hence highest priority elements are in the front of queue
• This priority queue is used in operating system to implements time
sharing property .
• The priority queue is again implemented in two way
1. array/sequential representation.
2. Dynamic/ linked representation.
In priority queue node is divided into three parts
Store Data <- INFO PRIORITY
NEXT ->Point to next Node
Structure of priority queue Node
By Prof. Raj Sarode 13

14. Thank You
By Prof. Raj Sarode 14