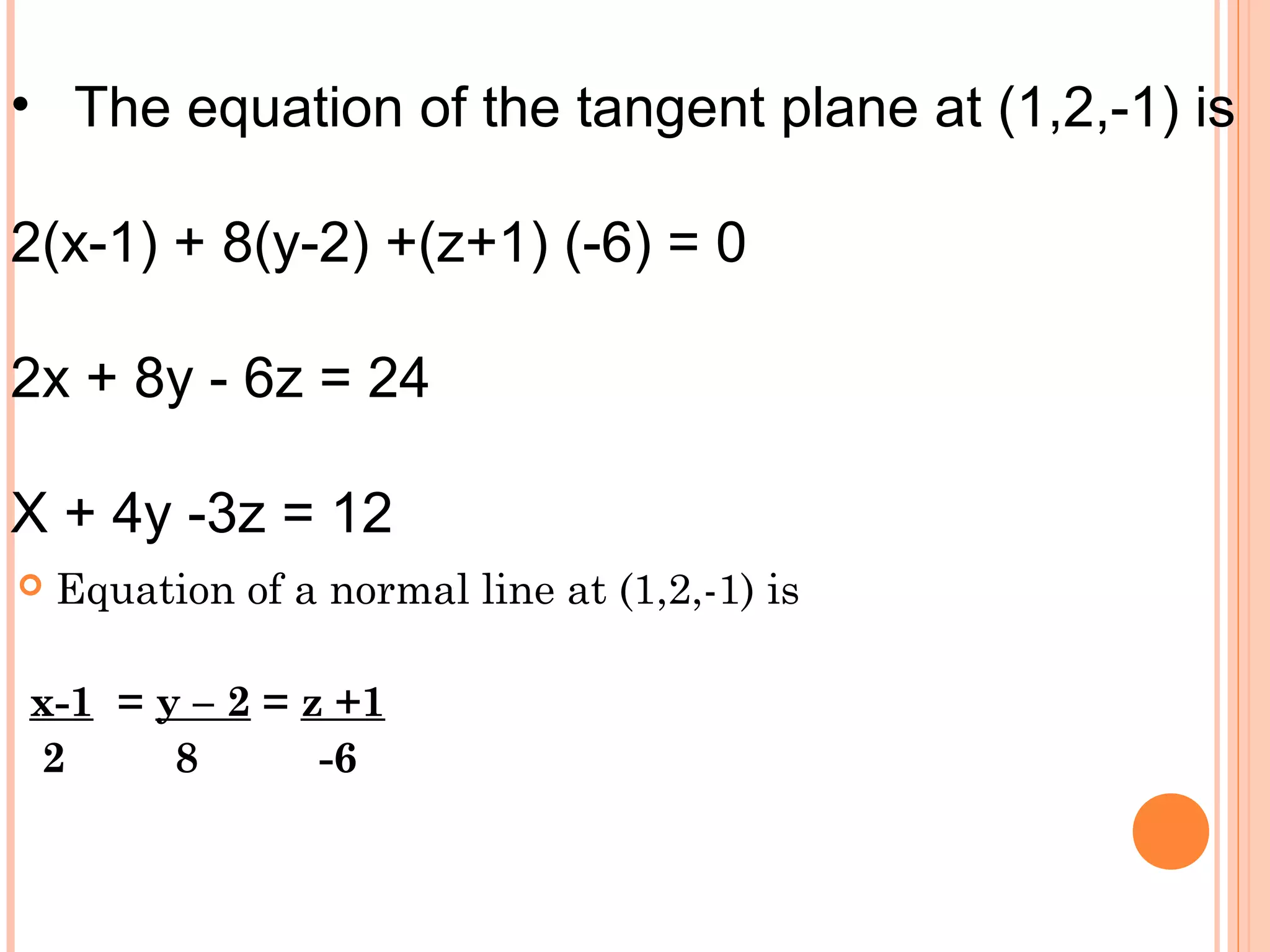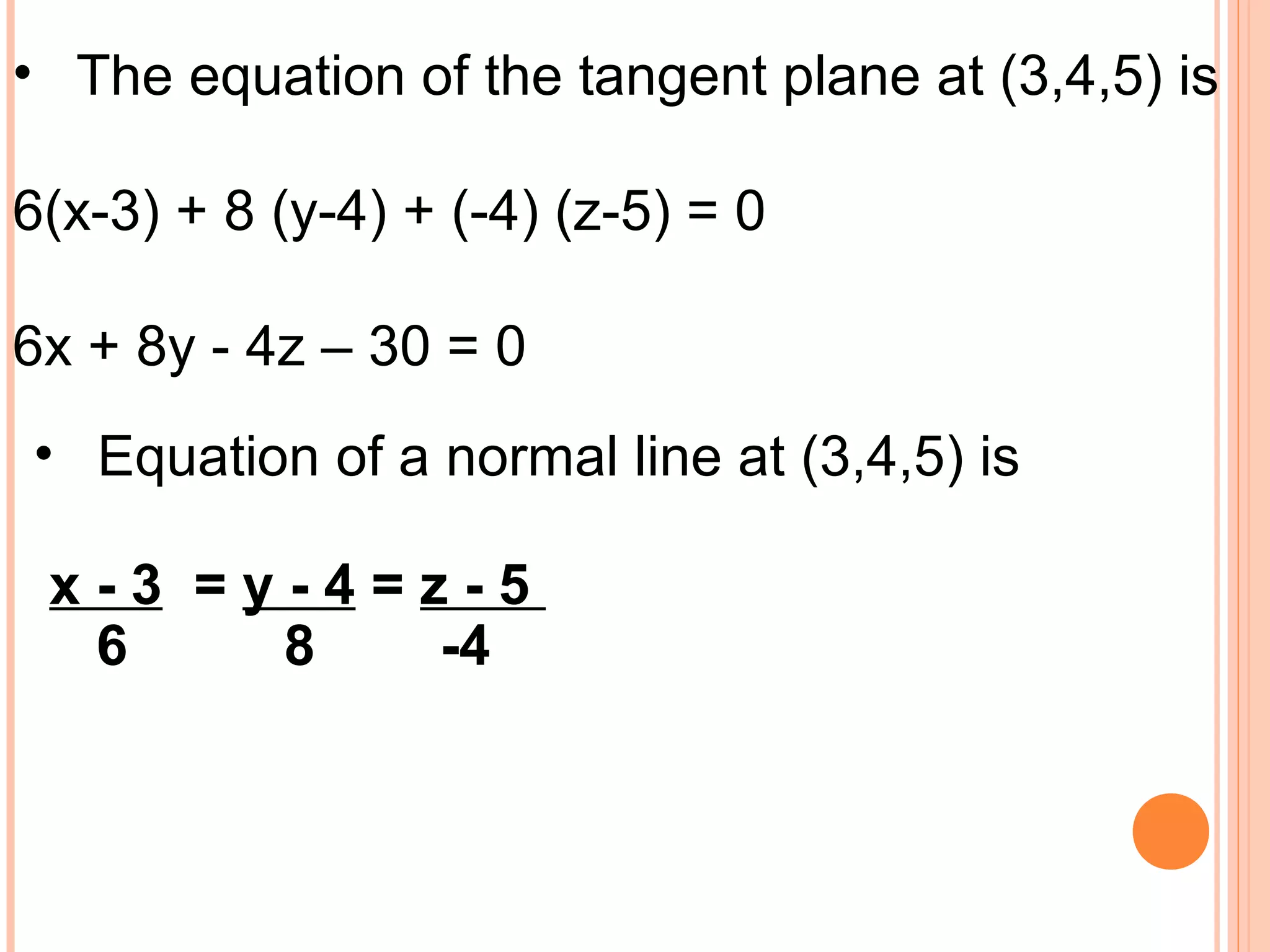The document discusses tangent planes and normal lines to surfaces. It provides the general equations for the tangent plane and normal line at a point P on a surface. It then works through 5 examples of finding the equation of the tangent plane and normal line for different surfaces at given points.

1. TANGENT PLANES AND
NORMAL LINES

2.  The equation of TANGENT PLANE to the
surface at P is given by:-
 (x-x1) fx + (y-y1) fy + (z-z1) fz =0
 The equation of the NORMAL LINE to the
surface at the point p is given by:-
 x-x1 = y – y1 = z – z1
fx fy fz

4. EX:-1 FIND THE EQUATION OF THE TANGENT
PLANE AND NORMAL LINE TO THE SURFACE
X2
+2Y2
+3Z2
=12 AT(1,2,-1).
Solution:- F(x,y,z) = x2
+ 2y2
+ 3z2
– 12 = 0
Fx = 2x , Fy = 4y , Fz = 6z
(Fx)p = 2(1) = 2
(Fy)p = 4(2) = 8
(Fz)p = 6(-1) = -6

5.  Equation of a normal line at (1,2,-1) is
x-1 = y – 2 = z +1
2 8 -6
• The equation of the tangent plane at (1,2,-1) is
2(x-1) + 8(y-2) +(z+1) (-6) = 0
2x + 8y - 6z = 24
X + 4y -3z = 12

6. Ex:-2 Find the equation of the tangent plane
and normal line to the surface 2xz2
– 3xy
-4x = 7 at (1,-1,2).
Solution:- F(x,y,z) = 2xz2
– 3xy -4x – 7 = 0
Fx = 2z2
– 3y -4 , Fy = – 3x , Fz = 4xz
(Fx)p = 7
(Fy)p = -3
(Fz)p = 8

7. • The equation of the tangent plane at (1,-1,2) is
7(x-1) -3 (y+1) + (z-2) (8) = 0
7x – 3y +8z = 26
• Equation of a normal line at (1,-1,2) is
x-1 = y+1 = z-2
7 -3 8

8. Ex:-3 Find the equation of the tangent plane
and normal line to the surface 2z – x2
= 0 at
(2,0,2).
Solution:- F(x,y,z) = 2z – x2
= 0
Fx = -2x , Fy = 0 , Fz = 2
(Fx)p = -2(2) = -4
(Fy)p = 0
(Fz)p = 2

9. • The equation of the tangent plane at (2,0,2) is
-4(x-2) +0 (y-0) + (z-2) (2) = 0
-4x + 2z +4 = 0
• Equation of a normal line at (2,0,2) is
x-2 = y-0 = z-2
-4 0 2

10. Ex:-4 Find the equation of the tangent plane
and normal line to the surface x2
+ y2
+ z2
=
3 at (1,1,1).
Solution:- F(x,y,z) = x2
+ y2
+ z2
- 3 = 0
Fx = 2x , Fy = 2y , Fz = 2z
(Fx)p = 2(1) = 2
(Fy)p = 2(1) = 2
(Fz)p = 2(1) = 2

11. • The equation of the tangent plane at (1,1,1) is
2(x-1) +2 (y-1) + 2 (z-1) = 0
x + y + z = 3
• Equation of a normal line at (1,1,1) is
x-1 = y-1 = z-1
2 2 2
X-1 = y-1 = z-1

12. Ex:-5 Find the equation of the tangent plane
and normal line to the surface x2
+ y2
– 4z
-5 = 0 at (3,4,5).
Solution:- F(x,y,z) = x2
+ y2
– 4z - 5 = 0
Fx = 2x , Fy = 2y , Fz = – 4
(Fx)p = 2(3) = 6
(Fy)p = 2(4) = 8
(Fz)p = -4 = -4

13. • The equation of the tangent plane at (3,4,5) is
6(x-3) + 8 (y-4) + (-4) (z-5) = 0
6x + 8y - 4z – 30 = 0
• Equation of a normal line at (3,4,5) is
x - 3 = y - 4 = z - 5
6 8 -4