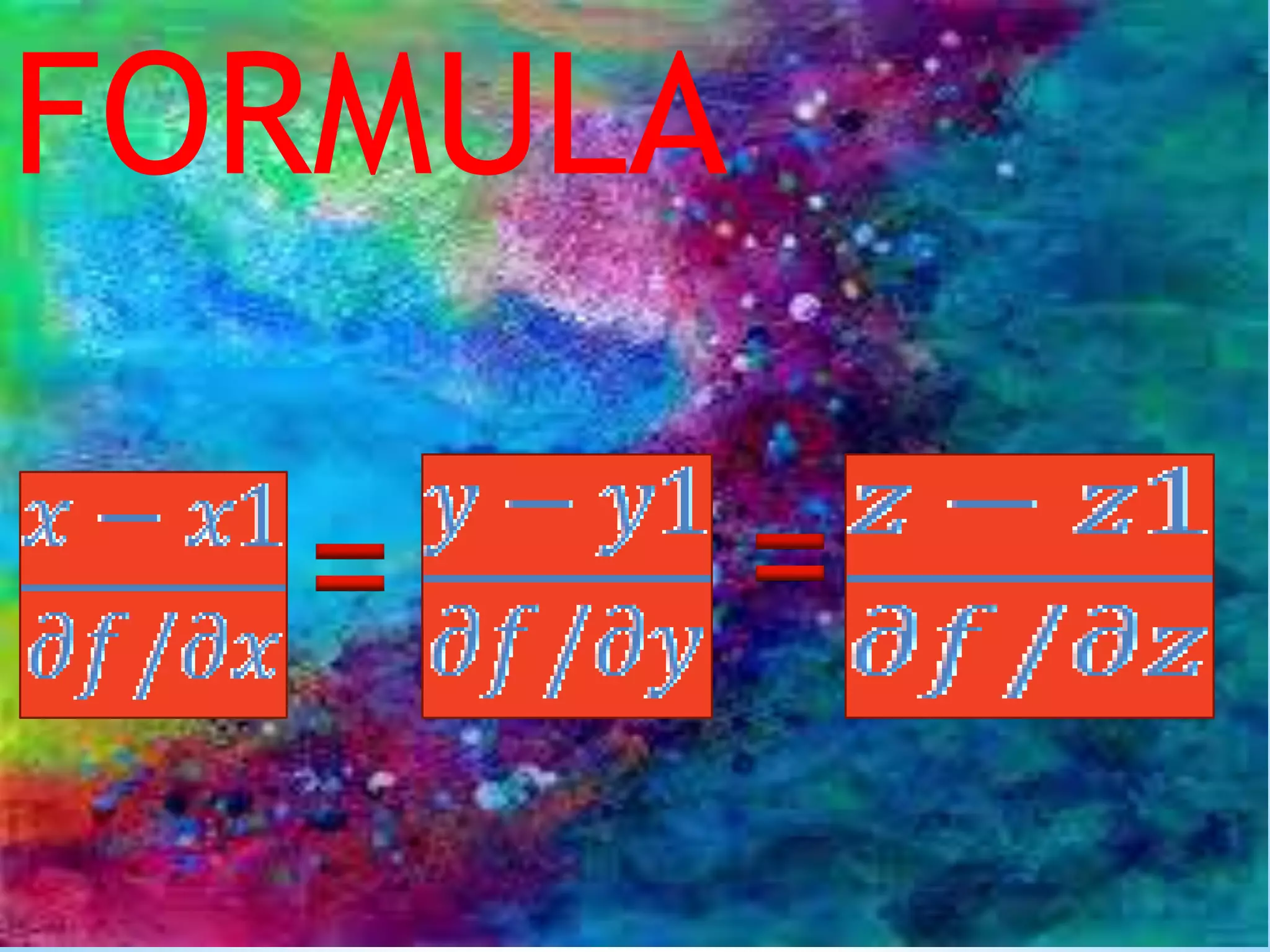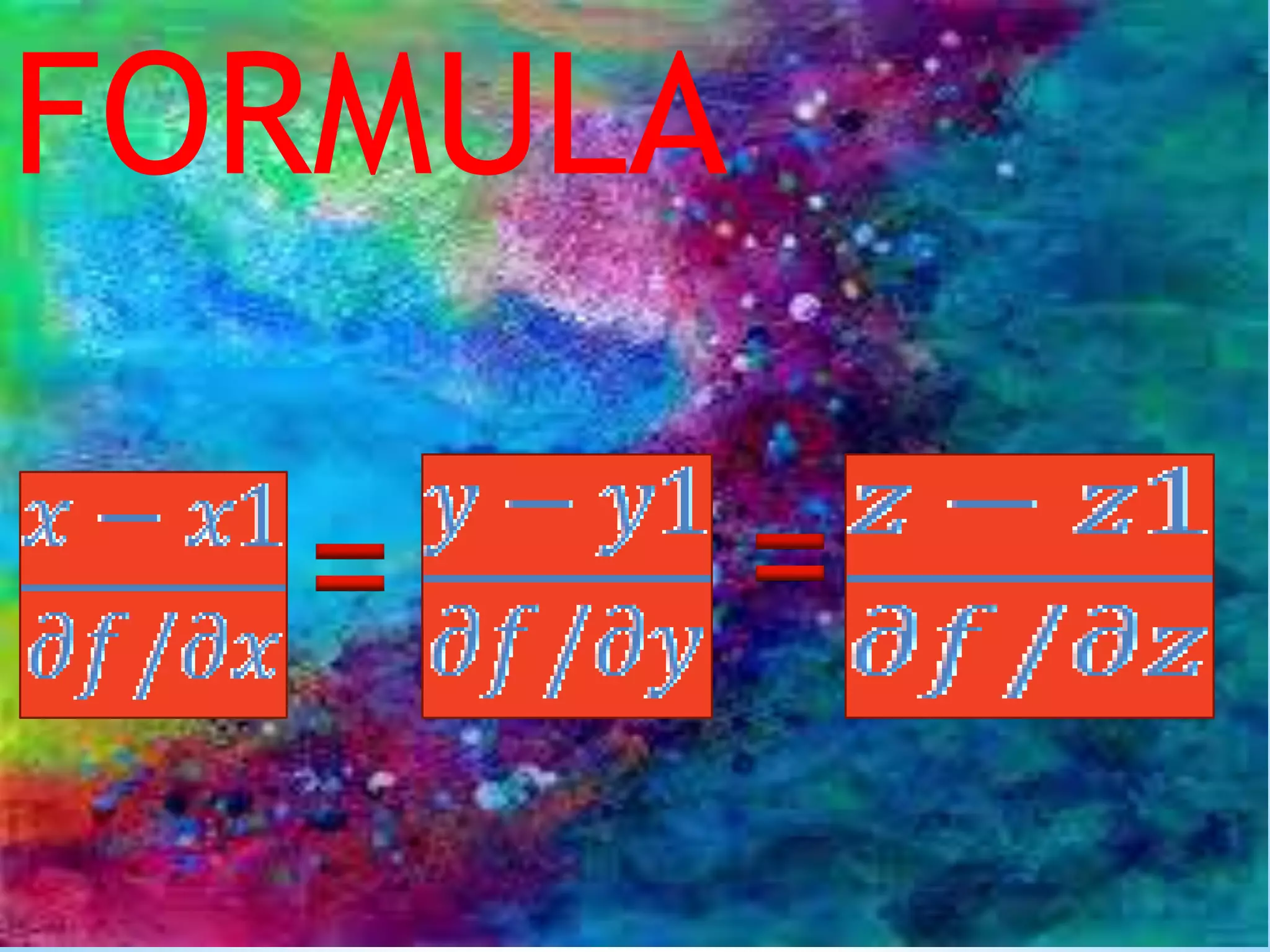
This document discusses three topics related to calculus: 1. Tangent plane - defined as the plane containing all tangent lines to curves on a surface at a given point. It provides a formula for finding the equation of a tangent plane. 2. Normal line - defined as perpendicular to the tangent line at the point of tangency. It provides a formula for finding the equation of a normal line. 3. Linearization - defined as approximating a differentiable function near a point using its tangent line. It provides an example of linearizing the cosine function near π/2.

1. *
VADODARA
INSTITUTE OF
ENGINEERING

2. 1.TANGENT PLANE
2.NORMAL LINE
3.LINERAZATION

3. TANGENT
PLANE

4. DEFINITION
THE PLANE THROUGH A POINT
OF A SURFACE THAT CONTAIN
THE TANGENT LINES TO ALL THE
CURVES ON THE SURFACE
THROUGH THE SAME POINT.

5. FORMULA

6. NORMAL
LINE

7. DEFINATION
THE NORMAL
LINE IS DEFINED AS
THE LINE THAT IS
PERPENDICULAR TO THE
TANGENT LINE AT THE
POINT OF TANGENCY.

8. FORMULA

9. EXAMPLE-FIND THE EQUATION OF THE TANGENT
PLANE AND NORMAL TO THE SURFACE
Z= AT THE POINT (1,-1,2)
Here f(x,y,z) = z - = 0
= -2x = -2y =1
At (1,-1,2), =-2, =2, =1
Therefore equation of the tangent plane at (1,-1,2)
(x-1)(-2) + (y+1)(2) + (z-2)(1) = 0
Or -2x + 2 + 2y + 2 +z -2 = 0
Or 2x – 2y – z = 2
Equation of the normal are = =

10. LINEARIZATION

11. DEFINITION
IF F IDIFFERENTIABLE AT X = A,
THEN APPROXIMATE FUNCTION
L(X) = F(A) + F’(A)(X-A)
IS THE LINEARIZATION OF F AT A.
THE APPROXIMATE F(X)≈L(X)
OF F BY L IS THE STANDARD LINEAR
APPROXIMATE OF F AT A.
THE POINT X = A IS THE CENTRE OF THE
APPROXIMATIONS.

12. Example- Find the linearization of f(x)=cosx at
x=π/2
Since f(π/2) = cos(π/2) = 0
f’(x) = -sinx
f’(π/2) = -sin(π/2) = -1
L(x) = f(a) + f’(a) (x-a)
= 0 + (-1) (x -π/2 )
= -x + π/2
cosx ≈ -x +π/2