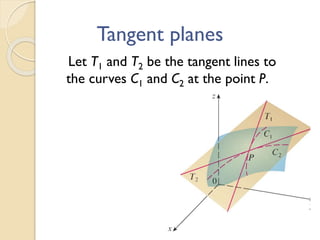
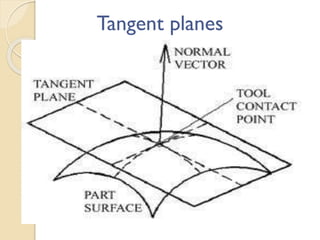
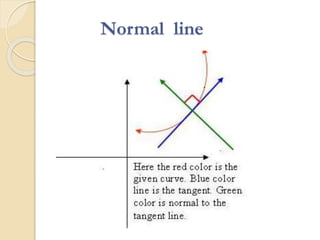
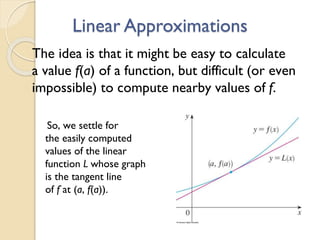
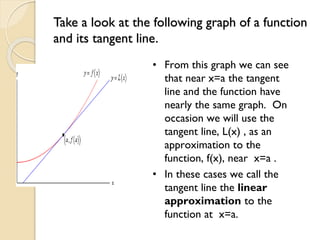
The document discusses concepts related to calculus including tangent planes, normal lines, and linear approximations. It provides definitions and equations for calculating the tangent plane to a surface, the normal line to a curve or surface, and using the tangent line as a linear approximation near a given point on a function. Examples are given to demonstrate finding the total derivative of a function and using the tangent line as a linearization.

1. Gandhinagar Institute
ofTechnology
Calculus – 2110014
“Total Differential ,Tangent
Plane, Normal Line, Linear
Approximation,”
Prepared By:
NiraliAkabari

3. Tangent planes
Suppose a surface S has equation z = f(x, y),
where f has continuous first partial derivatives.
Let P(x0, y0, z0) be a point on S.

4. Let T1 and T2 be the tangent lines to
the curves C1 and C2 at the point P.
Tangent planes

5. Tangent planes

6. Tangent planes
An equation of the tangent plane to the surface z
= f(x, y) at the point P(x0, y0, z0)
is:
fx(x0, y0, z0)(x – x0) + fy(x0, y0, z0)(y – y0) + fz (x0, y0,
z0) ( z– z0 )= 0

7. Normal line
 The normal line to a curve at a particular point is
the line through that point and perpendicular to the
tangent.
 A person might remember from analytic geometry
that the slope of any line perpendicular to a line with
slope m is the negative reciprocal −1/m.
 Thus, just changing this aspect of the equation for the
tangent line, we can say generally that the equation of
the normal line to the graph of ’f’ at (x0 ,f(x0 )) is
y − f(x0 ) = −1 (x−x0 ).
f′(x0 )

8. Normal line

9. Normal line
 Let f (x,y,z) define a surface that is differentiable
at a point (x0,y0,z0), then the normal line to f(x,y,z)
at ( x0 , y0 , z0 ) is the line with normal vector
f (x0,y0,z0)
that passes through the point (x0,y0,z0). In
Particular the equation of the normal line is
x(t) = x0 + fx(x0,y0,z0) t
y(t) = y0 + fy(x0,y0,z0) t
z(t) = z0 + fz(x0,y0,z0) t

10. Normal line

12. Linear Approximations
The idea is that it might be easy to calculate
a value f(a) of a function, but difficult (or even
impossible) to compute nearby values of f.
So, we settle for
the easily computed
values of the linear
function L whose graph
is the tangent line
of f at (a, f(a)).

13. In other words, we use the tangent line
at (a, f(a)) as an approximation to the curve
y = f(x) when x is near a.
 An equation of
this tangent line is
y = f(a) + f’(a)(x - a)

14. Linearization
The linear function whose graph is
this tangent line, that is,
L(x) = f(a) + f’(a)(x – a)
is called the linearization of f at a.

15. Take a look at the following graph of a function
and its tangent line.
• From this graph we can see
that near x=a the tangent
line and the function have
nearly the same graph. On
occasion we will use the
tangent line, L(x) , as an
approximation to the
function, f(x), near x=a .
• In these cases we call the
tangent line the linear
approximation to the
function at x=a.

17. The total differential
..............
),...,(functionvariable-nfor
isaldifferentitotalthe,0and0as
]
),(),(
[]
),(),(
[
),(),(),(),(
),(),(
and
2
2
1
1
21
n
n
n
dx
x
f
dx
x
f
dx
x
f
df
xxxf
dy
y
f
dx
x
f
df
dfyx
y
y
yxfyyxf
x
x
yyxfyyxxf
yxfyyxfyyxfyyxxf
yxfyyxxff
fffyyyxxx



























18. Ex: Find the total derivative of with
respect to given that
2/12
1
2/12
2/12
)1(
3
sin32
)1(
1
332
)1(
1
;3,32
x
x
xx
x
xyx
dx
df
xdx
dy
x
y
f
yx
x
f












x xyxyxf 3),( 2

xy 1
sin 
