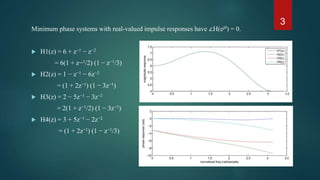
This document discusses minimum phase systems in digital signal processing. It defines minimum phase systems as those with all poles and zeros inside the unit circle, making both the system function and inverse causal and stable. Minimum phase systems are important because they have a stable inverse. The document outlines key properties of minimum phase systems including having the least phase delay, minimum group delay, and concentrating energy in the early part of the impulse response compared to other systems with the same magnitude response. An example demonstrates converting a mixed-phase system to minimum phase by adding an all-pass filter.

1. MINIMUM PHASE
SYSTEMS
PREPARED BY:- SHIVANGI SINGH
DIGITAL SIGNAL PROCESSING ( 2171003)
E.C DEPT.

2. INTRODUCTION
 A system with all poles and zeros inside the unit circle is called minimum phase
system.
 Both the system function and the inverse is causal and stable
 Minimum phase systems are important because they have a stable inverse G(z) =
1/H(z). We can convert between min/max/mixed-phase systems by cascading all
pass filters.
 When we say a system is “minimum phase”, we mean that it has the least phase
delay (or least phase lag) among all systems with the same magnitude response
2

3. Minimum phase systems with real-valued impulse responses have ∠H(ej0) = 0.
 H1(z) = 6 + z−1 − z−2
= 6(1 + z−1/2) (1 − z−1/3)
 H2(z) = 1 − z−1 − 6z−2
= (1 + 2z−1) (1 − 3z−1)
 H3(z) = 2 − 5z−1 − 3z−2
= 2(1 + z−1/2) (1 − 3z−1)
 H4(z) = 3 + 5z−1 − 2z−2
= (1 + 2z−1) (1 − z−1/3)
3

4. PHASE ANALYSIS
Phase response of a rational H(z) can be written as
To have the least phase delay for a causal system, we must have
4

5. re
im
re
im
re
im
re
im
re
im
re
im
5

6. PROPERTIES OF MINIMUM-PHASE
SYSTEMS
6

7. MINIMUM PHASE-LAG PROPERTY
 Continuous phase of a non-minimum-phase system
 All-pass systems have negative phase between 0 and 
 So any non-minimum phase system will have a more negative phase compared
to the minimum-phase system
 The negative of the phase is called the phase-lag function
 The name minimum-phase comes from minimum phase-lag
 
   
   
 




 j
ap
j
min
j
d e
H
arg
e
H
arg
e
H
arg
7

8. MINIMUM GROUP-DELAY
PROPERTY
 Group-delay of all-pass systems is positive
 Any non-minimum-phase system will always have greater group delay
 
   
   
 




 j
ap
j
min
j
d e
H
grd
e
H
grd
e
H
grd
8

9. MINIMUM ENERGY-DELAY
PROPERTY
 Minimum-phase system concentrates energy in the early part.
   

 


n
0
k
2
min
n
0
k
2
k
h
k
h
9

10. MINIMUM PHASE ⇒ MINIMUM
ENERGY DELAY
Given a causal system with impulse response h[n], we can define the partial
energy of the impulse response as
n
E[n] = Σ |h[k]|2
k=0
A minimum phase system with impulse response hmin[n] has the property
n n
Emin[n] = Σ|hmin[k]|2 ≥ Σ |h[k]|2 = E[n]
k=0 k=0
for all n ≥0 and all h[n] with the same magnitude response ashmin[n].
10

11. EXAMPLE : MINIMUM-PHASE SYSTEM
 Consider the following system
 One pole inside the unit circle:
-Make part of minimum-phase system
 One zero outside the unit circle:
-Add an all-pass system to reflect this zero inside the unit circle
 
1
1
1
z
2
1
1
z
3
1
z
H





 
1
1
1
1
1
1
1
1
1
z
3
1
1
z
3
1
1
3
1
z
z
2
1
1
1
3
3
1
z
z
2
1
1
1
3
z
2
1
1
z
3
1
z
H































     
z
H
z
H
z
3
1
1
3
1
z
z
2
1
1
z
3
1
1
3
z
H ap
min
1
1
1
1
1 

































11

12. THANK YOU
12