Downloaded 23 times
Uploaded byyash patel
Tangent plane
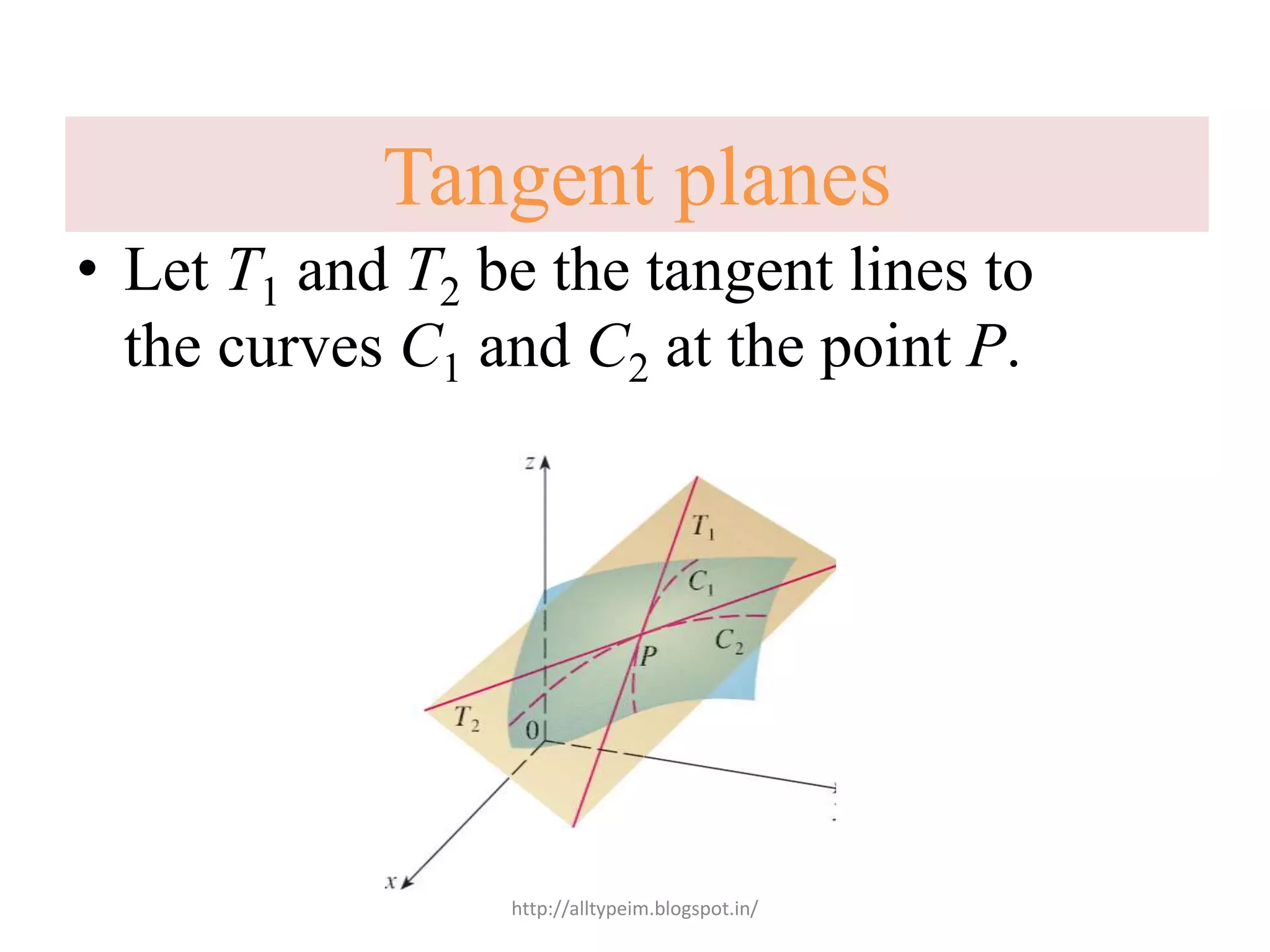
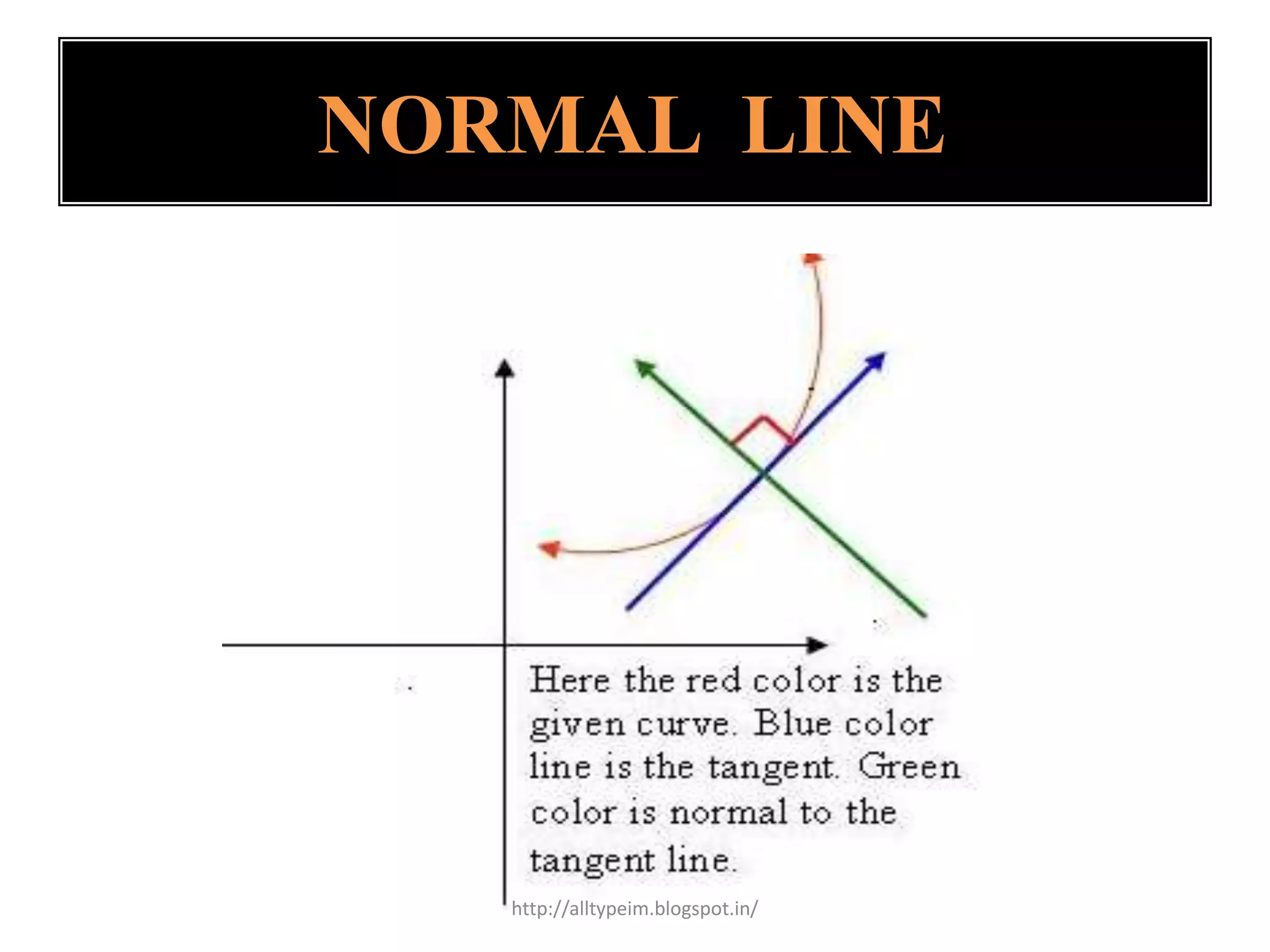
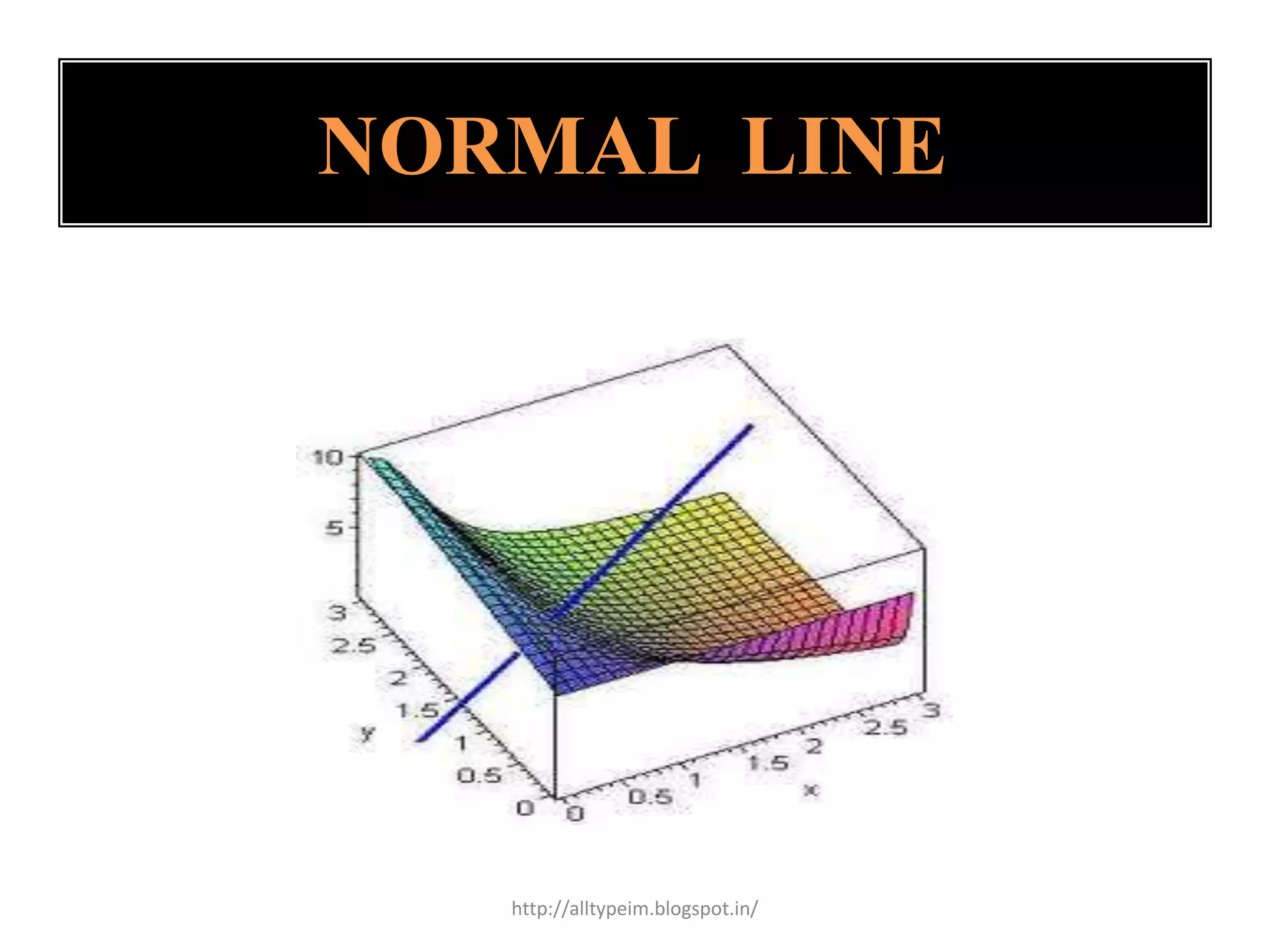
The document discusses tangent planes and normal lines to surfaces. It defines a tangent plane at a point P on a surface z=f(x,y) as having an equation involving the partial derivatives of f at P. A normal line to a curve at a point P is perpendicular to the tangent line at P, with slope given by the negative reciprocal of the tangent slope. The normal line to a surface z=f(x,y,z) at a point P passes through P with direction given by the gradient of f at P.
More Related Content
Tangent plane
- 1.
- 2. Itm universe TANGENT PLANE AND NORMALLINE GRAPHICAL REPRESENTATI ON http://alltypeim.blogspot.in/
- 3.
- 4. Tangent planes Suppose asurface S has equation z = f(x, y), where f has continuous first partial derivatives. Let P(x0, y0, z0) be a point on S. http://alltypeim.blogspot.in/
- 5. • Let T1and T2 be the tangent lines to the curves C1 and C2 at the point P. Tangent planes http://alltypeim.blogspot.in/
- 6.
- 7. An equation ofthe tangent plane to the surface z = f(x, y) at the point P(x0, y0, z0) is: fx(x0, y0, z0)(x – x0) + fy(x0, y0, z0)(y – y0) + fz (x0, y0, z0) ( z– z0 )= 0 Tangent planes http://alltypeim.blogspot.in/
- 8. Normal line Thenormal line to a curve at a particular point is the line through that point and perpendicular to the tangent. A person might remember from analytic geometry that the slope of any line perpendicular to a line with slope m is the negative reciprocal −1/m. Thus, just changing this aspect of the equation for the tangent line, we can say generally that the equation of the normal line to the graph of ’f’at (x0 ,f(x0 )) is y − f(x0 ) = −1 (x−x0 ). f′(x0 ) http://alltypeim.blogspot.in/
- 9.
- 10. Let f(x,y,z) define a surface that is differentiable at a point (x0,y0,z0), then the normal line to f(x,y,z) at ( x0 , y0 , z0 ) is the line with normal vector f (x0,y0,z0) that passes through the point (x0,y0,z0). In Particular the equation of the normal line is x(t) = x0 + fx(x0,y0,z0) t y(t) = y0 + fy(x0,y0,z0) t z(t) = z0 + fz(x0,y0,z0) t NORMAL LINE http://alltypeim.blogspot.in/
- 11.
- 12.