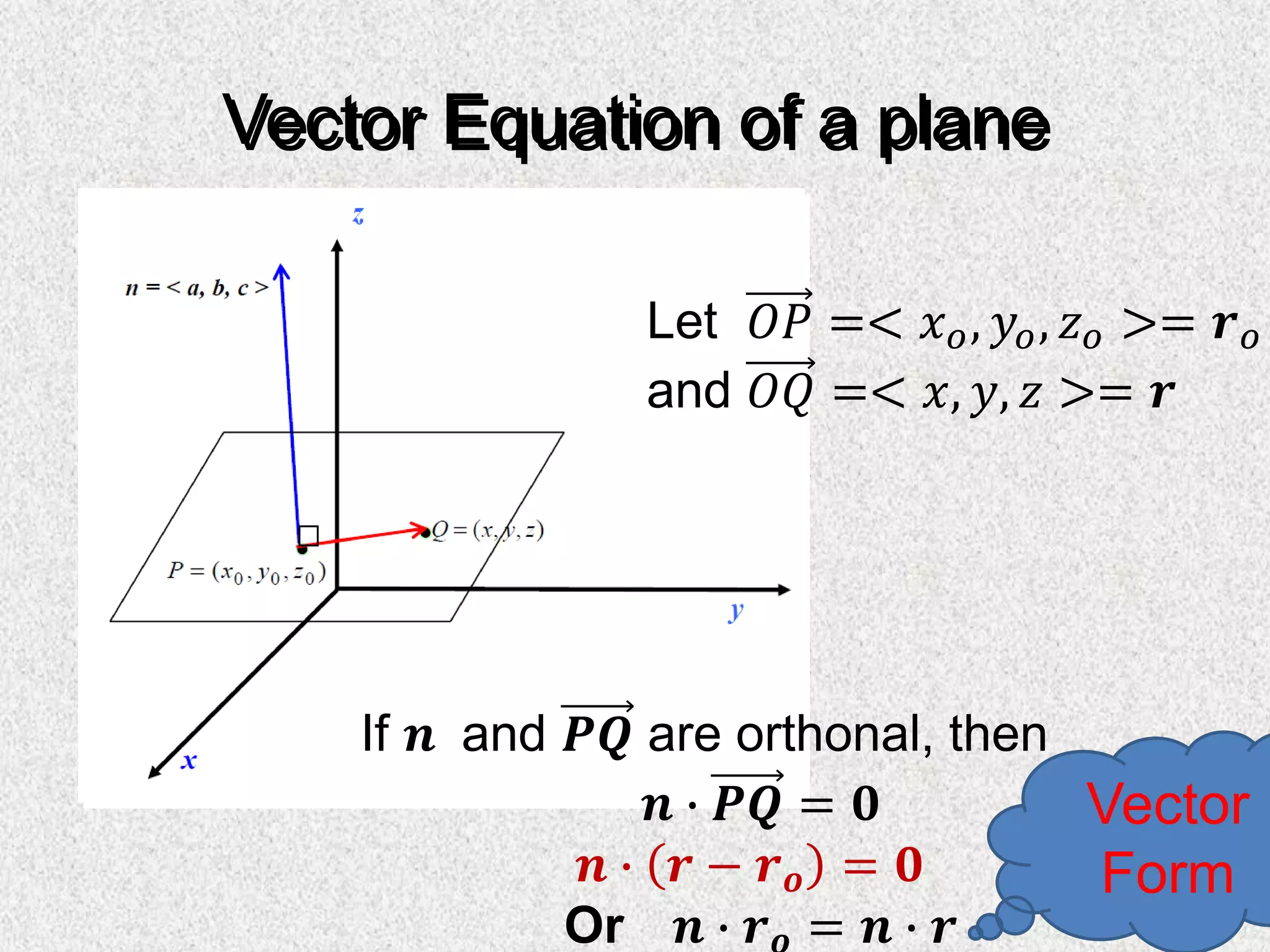
The document details the various forms of the equation of a plane, including vector, scalar, and parametric forms. It provides examples demonstrating how to derive these equations from given points and normal vectors. Additionally, it includes trial questions for further practice in applying these concepts.

1. EQUATION OF A PLANE
MUJUNGU HERBERT
National Teachers’ College
Kabale

2. Vector Equation of a plane
Let 𝑂𝑃 =< 𝑥 𝑜, 𝑦𝑜, 𝑧 𝑜 >= 𝒓 𝑜
and 𝑂𝑄 =< 𝑥, 𝑦, 𝑧 >= 𝒓
If 𝒏 and 𝑷𝑸 are orthonal, then
𝒏 ∙ 𝑷𝑸 = 𝟎
𝒏 ∙ 𝒓 − 𝒓 𝒐 = 𝟎
Or 𝒏 ∙ 𝒓 = 𝒏 ∙ 𝒓
Vector
Form
Vector Equation of a plane

3. Scalar Form of the Equation of a plane
From 𝒏 ∙ 𝒓 − 𝒓 𝒐 = 𝟎
a 𝒙 − 𝒙 𝒐 + b 𝒚 − 𝒚 𝒐 + c 𝒛 − 𝒛 𝒐 = 𝟎
Scalar
FormLinear
Form
Which is the standard form of the Equation
of a plane which is normal to a vector
𝑎
𝑏
𝑐
and d = −𝒂𝒙 𝒐 − 𝒃𝒚 𝒐 − 𝒄𝒛 𝒐.
𝒂𝒙 + 𝒃𝒚 + 𝒄𝒛 + 𝒅 = 𝟎
𝒂𝒙 + 𝒃𝒚 + 𝒄𝒛 − 𝒂𝒙 𝒐 − 𝒃𝒚 𝒐 − 𝒄𝒛 𝒐 = 𝟎
Scalar Form of the Equation of a plane
From 𝒏 ∙ 𝒓 − 𝒓 𝒐 = 𝟎
a 𝒙 − 𝒙 𝒐 + b 𝒚 − 𝒚 𝒐 + c 𝒛 − 𝒛 𝒐 = 𝟎

4. Parametric Form
Consider three points A, B and C with position vectors
𝒂 = 𝑎1, 𝑎2, 𝑎3 , 𝒃 = 𝑏1, 𝑏2, 𝑏3 and 𝐜 = 𝑐1, 𝑐2, 𝑐3 .
If a fourth point, P with position vector 𝐩 = 𝑥, 𝑦, 𝑧 , lies
on the same plane,
then scalars 𝜇 and 𝜆 can
be found such that,
𝑥 = 𝑎1 + 𝜇 𝑏1 − 𝑎1 + 𝜆(𝑐1 − 𝑎1)
𝑦 = 𝑎2 + 𝜇 𝑏2 − 𝑎2 + 𝜆(𝑐2 − 𝑎2)
𝑧 = 𝑎3 + 𝜇 𝑏3 − 𝑎3 + 𝜆(𝑐3 − 𝑎3)
𝐴𝑃 = 𝜇𝐴𝐵 + 𝜆𝐴𝐶
𝒑 − 𝒂 = 𝜇 𝒃 − 𝒂 + 𝜆(𝒄 − 𝒂)
𝒑 = 𝒂 + 𝜇 𝒃 − 𝒂 + 𝜆(𝒄 − 𝒂)

5. EXAMPLE 1
Find the parametric equation of the plane passing
through the points (1, 2, -3), (2, 3, 1), and (0, -2, -1).
Solution
Let points A = (1, 2, -3), B = (2, 3, 1), C = (0, -2, -1) and
P=(x,y,z) be the points on the plane
Recall Equation of the plane in the form 𝐴𝑃 = 𝜇𝐴𝐵 + 𝜆𝐴𝐶
And by using it,
We have,
𝑥 − 1
𝑦 − 2
𝑧 + 3
= 𝜇
2 − 1
3 − 2
1 + 3
+ 𝜆
0 − 1
−2 − 2
−1 + 3
𝑥 = 1 + 𝜇 − 𝜆
𝑦 = 2 + 𝜇 − 4𝜆
𝑧 = −3 + 4𝜇 + 2𝜆

6. Example 2
Find the equation of plane through point (1,-1,1) and
with normal vector i+j-k
Let A=(1,-1,1), P=(x,y,z) be another point on the plane
and normal vector n = 1,1, −1 .
𝑥 − 1
𝑦 + 1
𝑧 − 1
∙
1
1
−1
=0
Finally 𝑥 + 𝑦 − 𝑧 + 1 = 0
Solution:
Then 𝐴𝑃 ∙ 𝑛 = 0
or (𝑂𝑃 − 𝑂𝐴) ∙ 𝑛 = 0

7. Example 3
Find the equation of plane through the points (0,1,1),
(1,0,1) and(1,1,0)
First alternative solution
Let points A=(0,1,1), B=(1,0,1) , C=(1,1,0) and P=(x,y,z)
And using 𝐴𝑃 = 𝜇𝐴𝐵 + 𝜆𝐴𝐶
𝑥 − 0
𝑦 − 1
𝑧 − 1
= 𝜇
1 − 0
0 − 1
1 − 1
+ 𝜆
1 − 0
1 − 1
0 − 1
𝑥 = 𝜇 + 𝜆 … … … … . . (𝑖)
𝑦 = 1 − 𝜇 … … … … . (𝑖𝑖)
𝑧 = 1 − 𝜆 … … … … … (𝑖𝑖𝑖)
From Eqns (ii) and (iii) , 𝜇 = 1 − 𝑦 and 𝜆 = 1 − 𝑧 respectively and sub
in Eqn (iii),
That is 𝑥 = 1 − 𝑦 + 1 − 𝑧
𝑥 + 𝑦 + 𝑧 − 2 = 0Finally

8. Example 3
Find the equation of plane through the points (0,1,1),
(1,0,1) and(1,1,0)
Second alternative solution
𝒙 + 𝒚 + 𝒛 − 𝟐 = 0

9. TRIAL QUESTIONS
Find the equation of the plane passing through;
1. 𝑃𝑜 2,4, −1 having a normal vector 𝑛 = 2,3,4
2. P(1,3,2), Q(3,-1,6) and R(5,2,0).
3. (1,0,1), (0,1,1) and (1,1,0).
4. (5,1,0) and parallel to two lines x=2+t, y=-2t, z=1 and x=t,
y=2-t, z=2-3t.
5. (-1,2,1) and contains the line of intersection of two planes
x+y-z=2 and 2x-y+3z=1.
6. (-1,2,1) and is perpendicular to the line of intersection of
two planes x+y-z=2 and 2x-y+3z=1.
7. the line of intersection of the planes x-z=1 and y+2z=3, and
is perpendicular to the plane x+y-2z=1.
8.The point (-4,3,1) that is perpendicular to the vector
a=-4i+7j-2k
END

10. Find more work at https://bit.ly/padlet-DESI