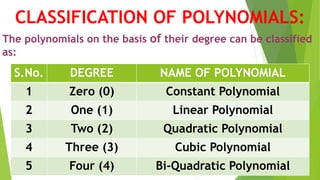
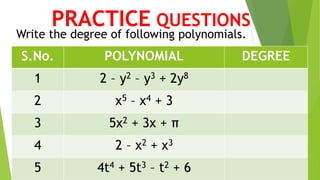
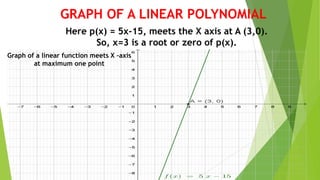
This document defines polynomials and discusses their key properties. It begins by defining a polynomial as an algebraic expression with two or more terms where the power of each variable is a positive integer. The degree of a polynomial is defined as the highest power of the variable. Polynomials are then classified based on their degree as constant, linear, quadratic, cubic, etc. The document also discusses the zeros or roots of a polynomial, which are the values that make the polynomial equal to zero. It shows how the zeros relate to the coefficients of the polynomial and can be found using factoring or solving techniques. Examples are provided to illustrate dividing polynomials using the division algorithm.

1. POLYNOMIALS
BY:
Dr. VIVEK NAITHANI
T.G.T (MATHEMATICS), KVS
COPYRIGHT INFORMATION: CC by SA 4.0

2. DEFINITION
An algebraic expression that contain two or more terms is called a
polynomial.
Each term of a polynomial has a co-efficient.
For an algebraic expression to qualify for being a polynomial it is
necessary that the power of variable in each term must be a positive
integer.
e.g. –x3+4x2+7x-2, 3y2+5y-7 etc.
𝑥 +
1
𝑥
is not a polynomial as the power of x in second term is -1
𝑦+5y is not a polynomial as the power of y is fraction in first term.

3. A polynomial in variable can be expressed generally as
anxn +an-1xn-1+an-2xn-2+…………..+ a2x2+a1x+a0
where
an, an-1, an-2, …………., a2, a1, a0 are all constants not
all zero and n is any positive integer.

4. DEGREE OF A POLYNOMIAL
The degree of a polynomial is the highest power of the
variable appearing in the polynomial.
e.g.: The degree of the polynomial x2-6x +7 is 2 as the
highest power of x appearing in the given polynomial is 2.
3x5+4x2-2. Here the highest power of variable is 5 so the
degree is 5

5. CLASSIFICATION OF POLYNOMIALS:
S.No. DEGREE NAME OF POLYNOMIAL
1 Zero (0) Constant Polynomial
2 One (1) Linear Polynomial
3 Two (2) Quadratic Polynomial
4 Three (3) Cubic Polynomial
5 Four (4) Bi-Quadratic Polynomial
The polynomials on the basis of their degree can be classified
as:

6. PRACTICE QUESTIONS
S.No. POLYNOMIAL DEGREE
1 2 – y2 – y3 + 2y8
2 x5 – x4 + 3
3 5x2 + 3x + π
4 2 – x2 + x3
5 4t4 + 5t3 – t2 + 6
Write the degree of following polynomials.

7. ZEROES OF A POLYNOMIAL:
 The zero or root of a polynomial p(x) is the value of x at
which p(x) = 0.
 If for x=a, p(a) = 0 then we say x=a is the zero or root of p(x).
 E.g.: p(x) = x2- 5x+6 is a polynomial.
For x= 2, we get p(2) = (2)2 – 5(2) +6
= 4 -10 +6 = 10-10 =0
Hence x=2 is a root or zero of p(x).

8. GEOMETRICAL MEANING OF ZEROES OF A
POLYNOMIAL
 If p(x) is a polynomial and we plot the graph of p(x) on a graph
sheet. The number of points of intersection of graph pf p(x) and
X –axis represent the number of zeroes or roots of p(x).
 A linear polynomial graph meets X axis at only one point.
 A quadratic polynomial graph meets the X – axis at maximum two
points.
 A cubic polynomial graph meets the X – axis at maximum three
points.

9. GRAPH OF A LINEAR POLYNOMIAL
Here p(x) = 5x-15, meets the X axis at A (3,0).
So, x=3 is a root or zero of p(x).
Graph of a linear function meets X –axis
at maximum one point

10. GRAPH OF A QUADRATIC FUNCTION
Here p(x) = x2-x-6 meets X axis at A (-2,0) and B (3,0). So x= -2 and x=3 are the
roots of p(x).
The graph of a quadratic polynomial is a parabola
and meets X –axis at maximum two points

11. GRAPH OF A CUBIC FUNCTION
Here p(x) = x3-7x; meets X- axis at A(-2.6,0); B(0,0); C(2.6,0). So,
x= -2.6, 0 and +2.6 are the roots of p(x).

12. RELATIONSHIP BETWEEN ZEROES AND CO-
EFFICIENTS OF A POLYNOMIAL
If ax2+bx+c is a quadratic polynomial whose roots are α and β.
Then
Sum of roots α + β =
−𝒃
𝒂
=
−(𝒄𝒐𝒆𝒇𝒇𝒊𝒄𝒊𝒆𝒏𝒕 𝒐𝒇 𝒙)
(𝒄𝒐−𝒆𝒇𝒇𝒊𝒄𝒊𝒆𝒏𝒕 𝒐𝒇 𝒙𝟐)
Product of roots α X β =
c
a
=
𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡
(𝒄𝒐−𝒆𝒇𝒇𝒊𝒄𝒊𝒆𝒏𝒕 𝒐𝒇 𝒙𝟐)
The quadratic polynomial is: x2 –(Sum) x + (Product)

13. If ax3+bx2+cx+d is a cubic polynomial whose roots
are α, β and γ, then
α + β + γ =
−𝒃
𝒂
=
− (𝒄𝒐𝒆𝒇𝒇𝒊𝒄𝒊𝒆𝒏𝒕 𝒐𝒇 𝒙𝟐 )
(𝒄𝒐−𝒆𝒇𝒇𝒊𝒄𝒊𝒆𝒏𝒕 𝒐𝒇 𝒙𝟑)
αβ + βγ + γα =
𝒄
𝒂
=
(𝒄𝒐−𝒆𝒇𝒇𝒊𝒄𝒊𝒆𝒏𝒕 𝒐𝒇 𝒙)
(𝒄𝒐−𝒆𝒇𝒇𝒊𝒄𝒊𝒆𝒏𝒕 𝒐𝒇 𝒙𝟑)
α X β X γ =
−𝒅
𝒂
=
−(𝒄𝒐𝒏𝒔𝒕𝒂𝒏𝒕 )
(𝒄𝒐−𝒆𝒇𝒇𝒊𝒄𝒊𝒆𝒏𝒕 𝒐𝒇 𝒙𝟑)

14. FIND THE ZEROES AND VERIFY THE
RELATIONSHIP BETWEEN CO-EFFS. & ZEROES
(i) p(x) = x2- 2x- 8 Solving by splitting the
middle term
= x2 -4x+2x-8 now regrouping and taking
out common factors
= x(x-4) + 2 (x-4)
= (x-4) (x+2)
For p(x) = 0 ; Either x-4 = 0 ⇒ x=4
or x+2 = 0 ⇒ x = -2
Hence zeroes are α = 4 and β = -2
Now the coefficients are
a = 1; b = -2 and c = -8
The sum of roots α + β = 4 +(-2) = 4-2 =
2
−𝑏
𝑎
=
−(−2)
1
= 2
Hence α + β =
−𝑏
𝑎
Product of roots = α X β = 4 X (-2) = -8
𝑐
𝑎
=
(−8)
1
= -8
Hence α X β =
𝑐
𝑎
Hence relation is verified.

15. (ii) 6x2 – 3 -7x
First arranging the terms in descending
order of power
6x2- 7x – 3 Solving by splitting the middle
term
= 6x2 – 9x+ 2x -3 Regrouping and taking out
common factor
= 3x(2x-3) +1 (2x-3)
= (2x-3) (3x+1)
For p(x) = 0
Either 2x-3 = 0 ⇒ 2x= 3 ⇒ x= 3/2
Or 3x+1 = 0 ⇒ 3x = -1 ⇒ x = -1/3
Hence zeroes are α = 3/2 and β = -1/3
Now the coefficients are
a = 6; b = -7 and c = -3
The sum of roots α + β =
3
2
+ (
−1
3
)
=
9−2
6
=
7
6
−𝑏
𝑎
=
−(−7)
6
=
7
6
The product of the roots α X β =
3
2
X (
−1
3
) =
−1
2
𝑐
𝑎
=
−3
6
=
−1
2
Hence relation is verified.

16. PRACTICE QUESTIONS:
Q. Find a polynomial sum and product of whose roots are 4 and 1
respectively.
Solution: Here Sum (S) = 4 and product (P) = 1
Polynomial = x2- (Sum) x + Product
= x2 – 4x +1
Q. Find a polynomial whose roots are 2 and 5.
Solution: Here α = 2 and β = 5
Sum = α + β = 2 + 5 = 7
Product = α X β = 2 X 5 = 10
Polynomial = x2- (Sum) x + Product
= x2 – 7x +10

17. DIVISION ALGORITHM FOR POLYNOMIALS
If p(x) and g(x) are any two polynomials with g(x) ≠
𝟎 then we can find polynomials q(x) and r(x) such that
p(x) = g(x) × q(x) + r(x) where r(x) = 0 or
degree of r(x) < degree of g(x).
Here again, we see that
Dividend = Divisor × Quotient + Remainder

18. Divide: 3x2-x3-3x+5 by x-1-x2
Here Divisor is x-1-x2 = -x2 + x -1
and Dividend = 3x2– x3 -3x +5 = -x3 +3x2 – 3x + 5

19. Divide x4-3x2+4x+5 by x2-x+1

20. On dividing x3- 3x2+x+2 by a polynomial g(x) the
quotient = x-2 and remainder = -2x+4. Find g (x).

22. THANK
YOU BY:
Dr. VIVEK NAITHANI
T.G.T (MATHEMATICS), KVS
COPYRIGHT INFORMATION: CC by SA 4.0