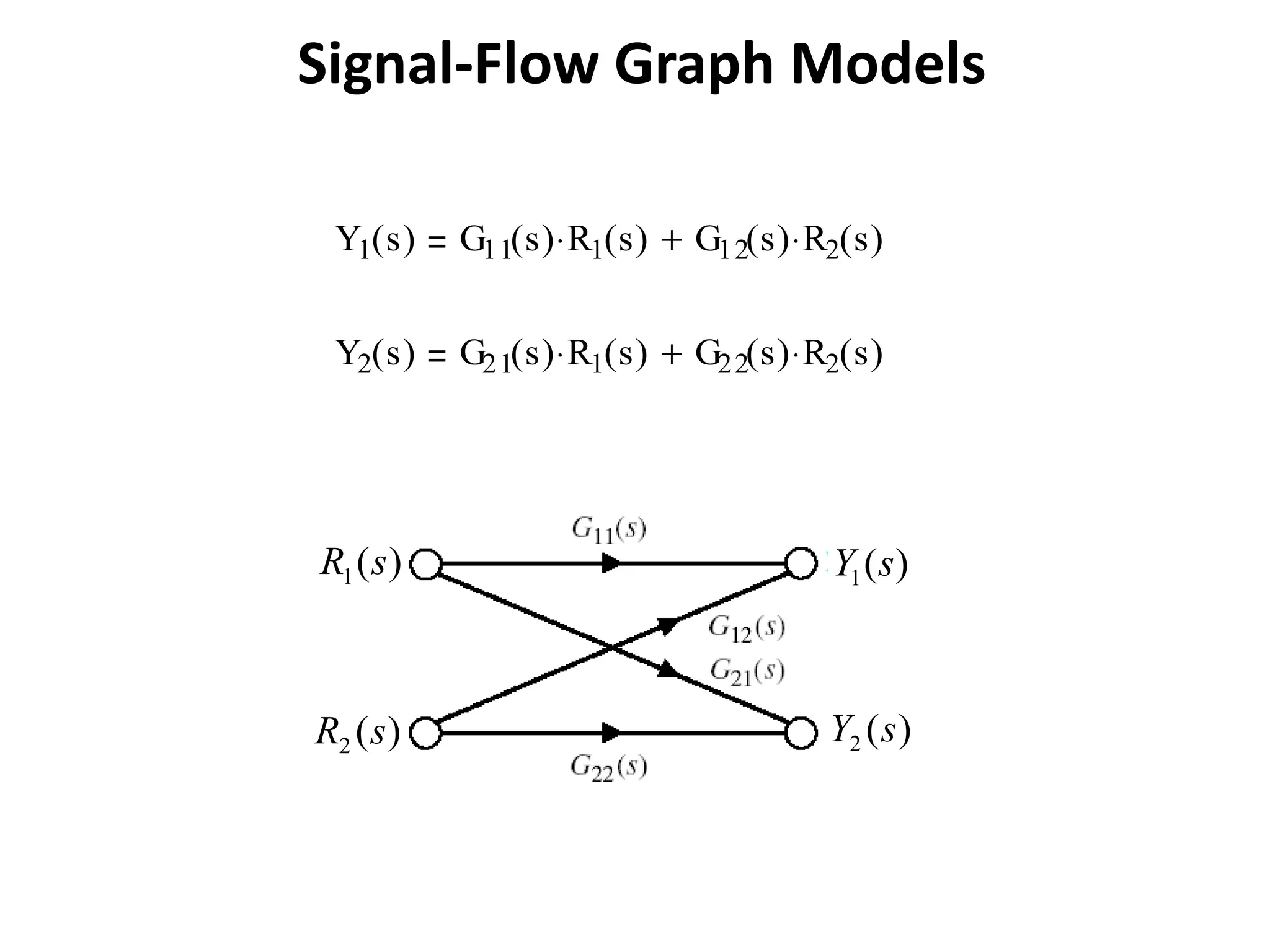
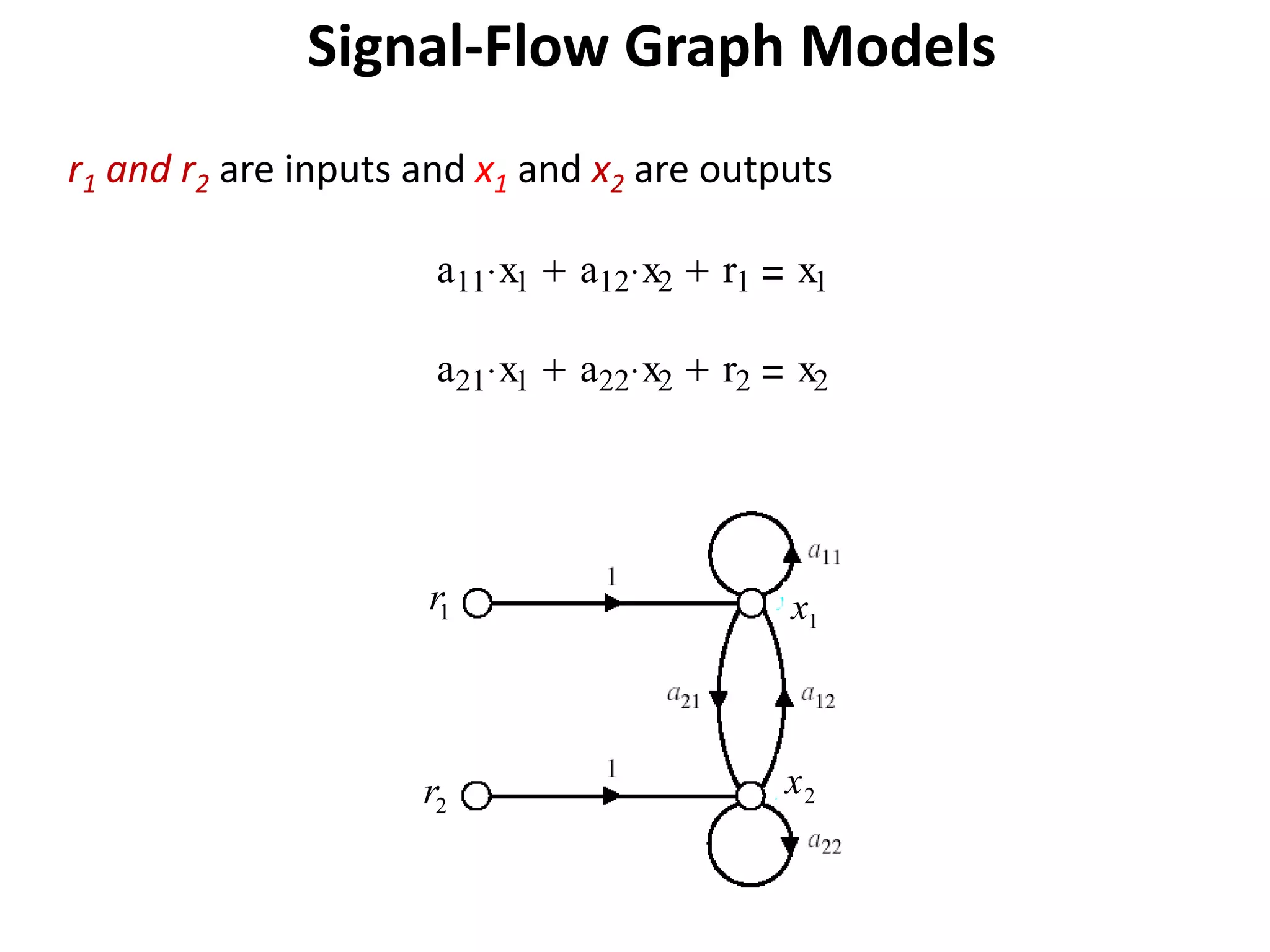
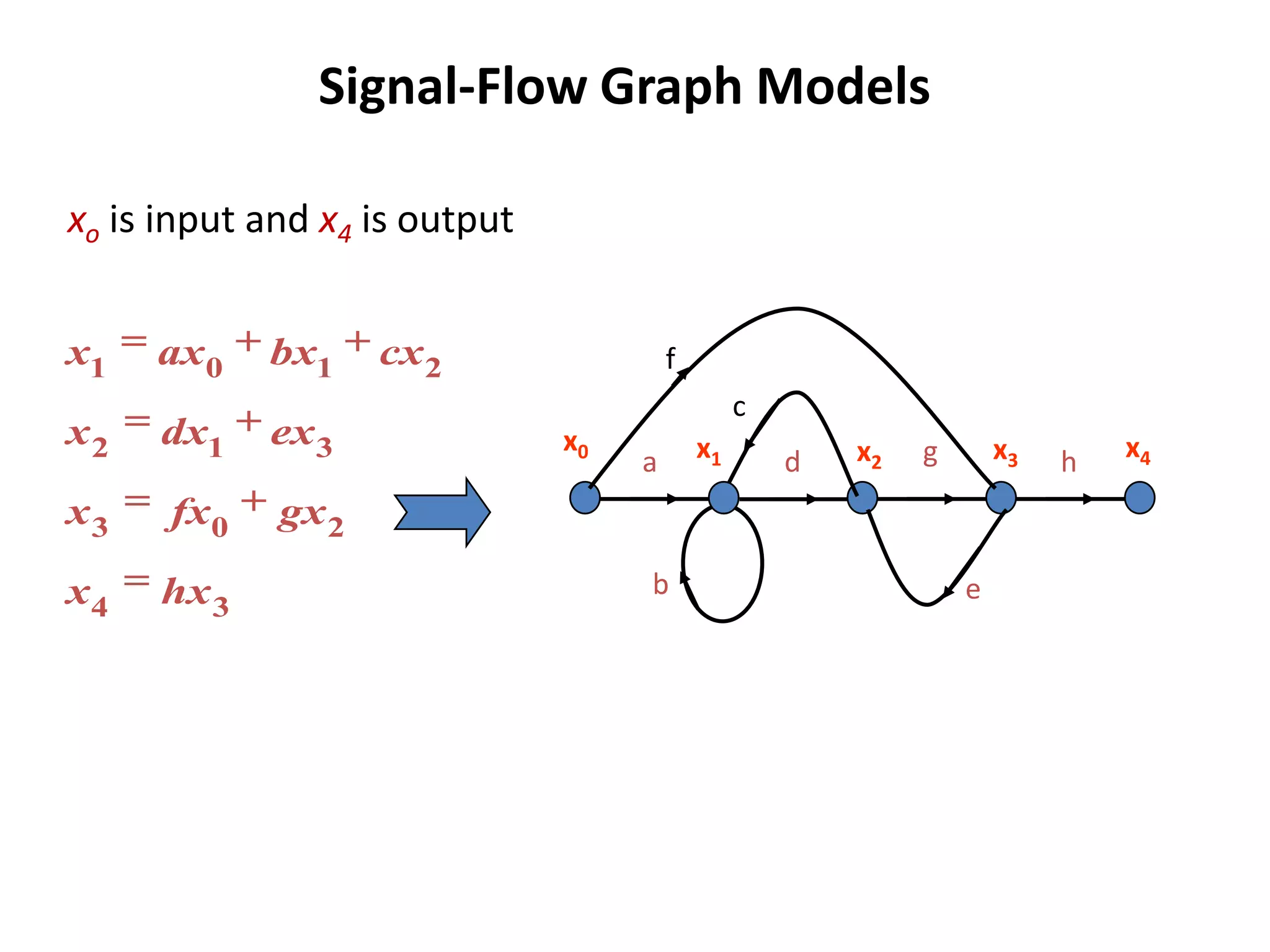
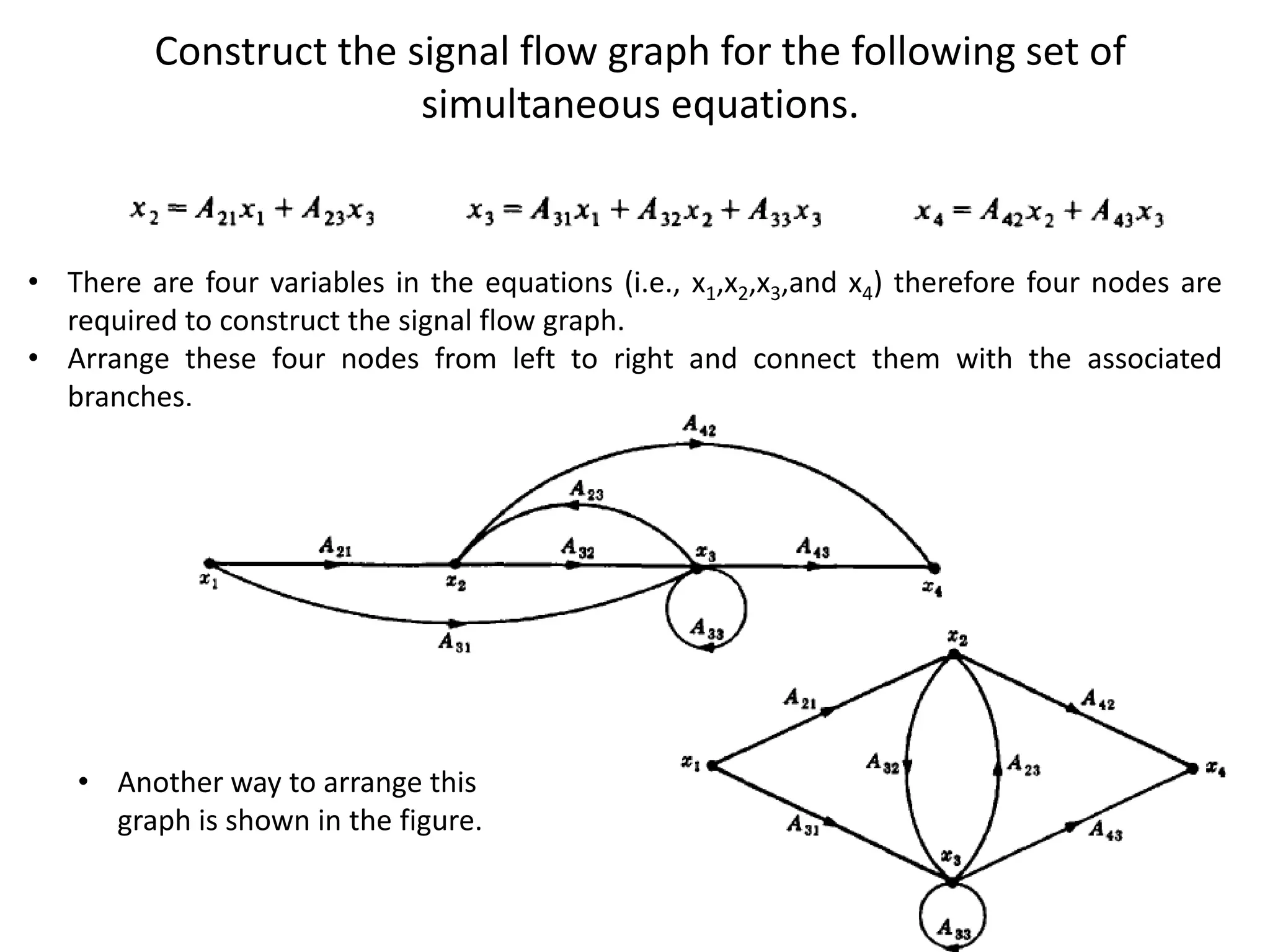
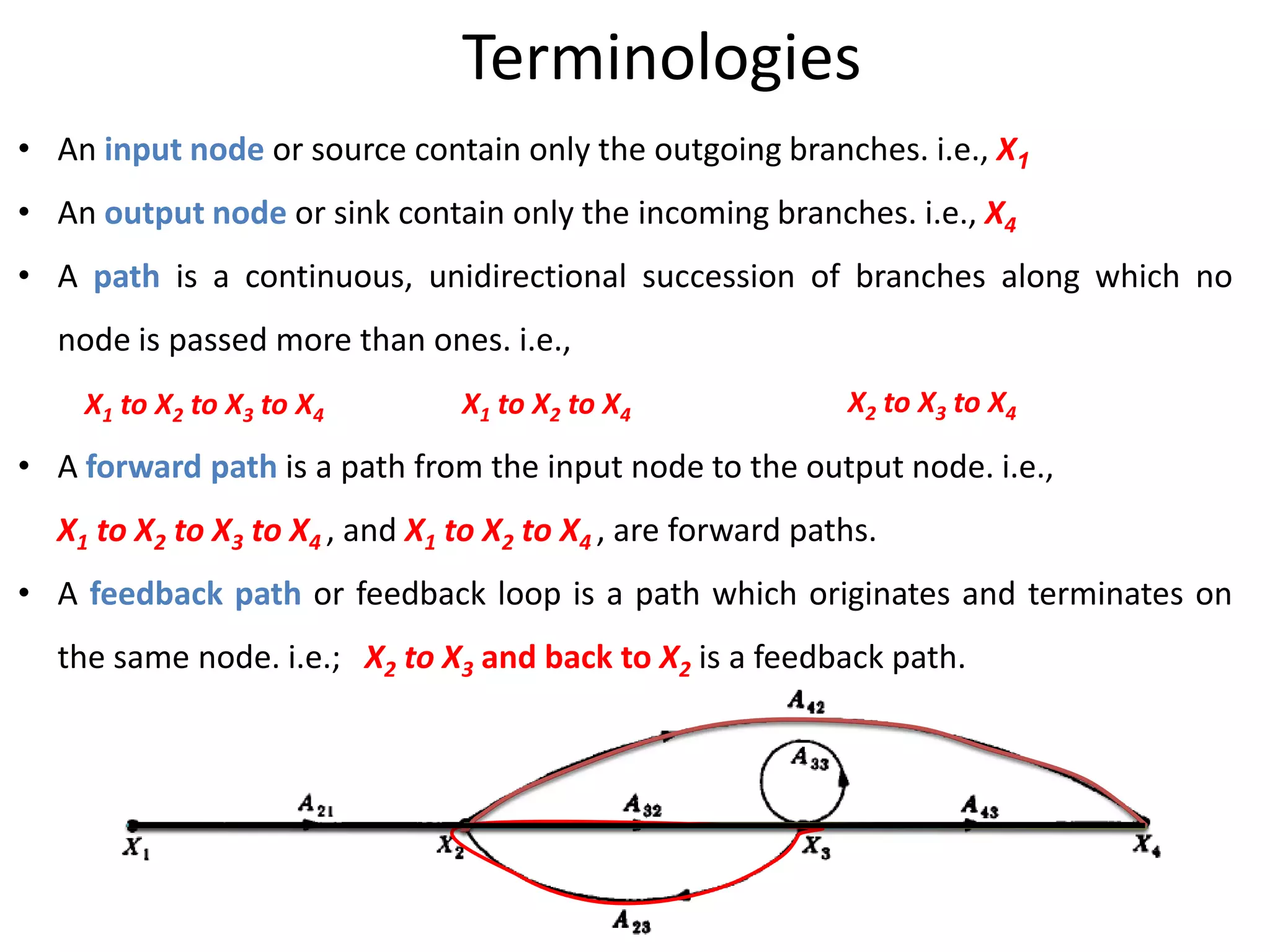
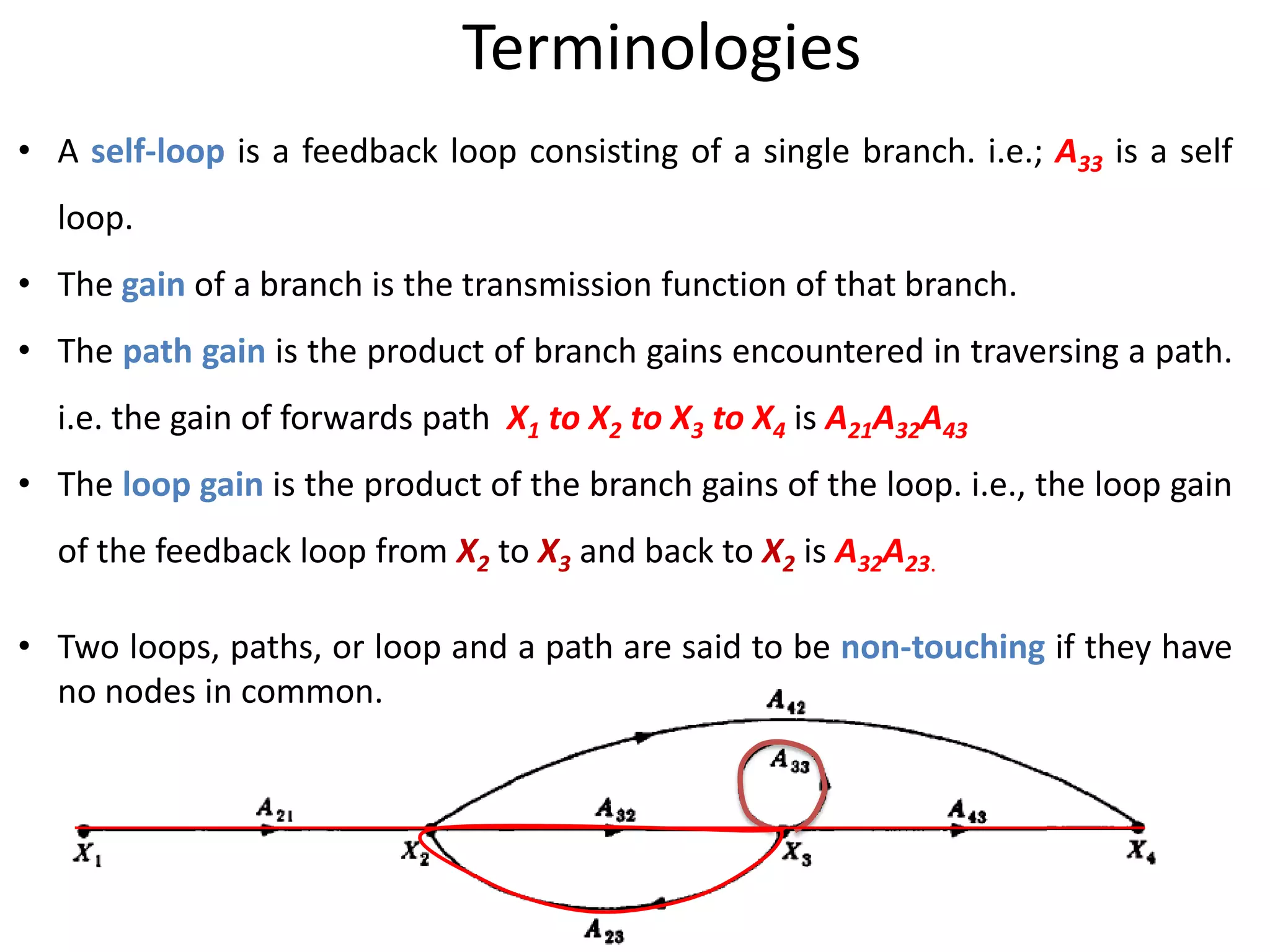
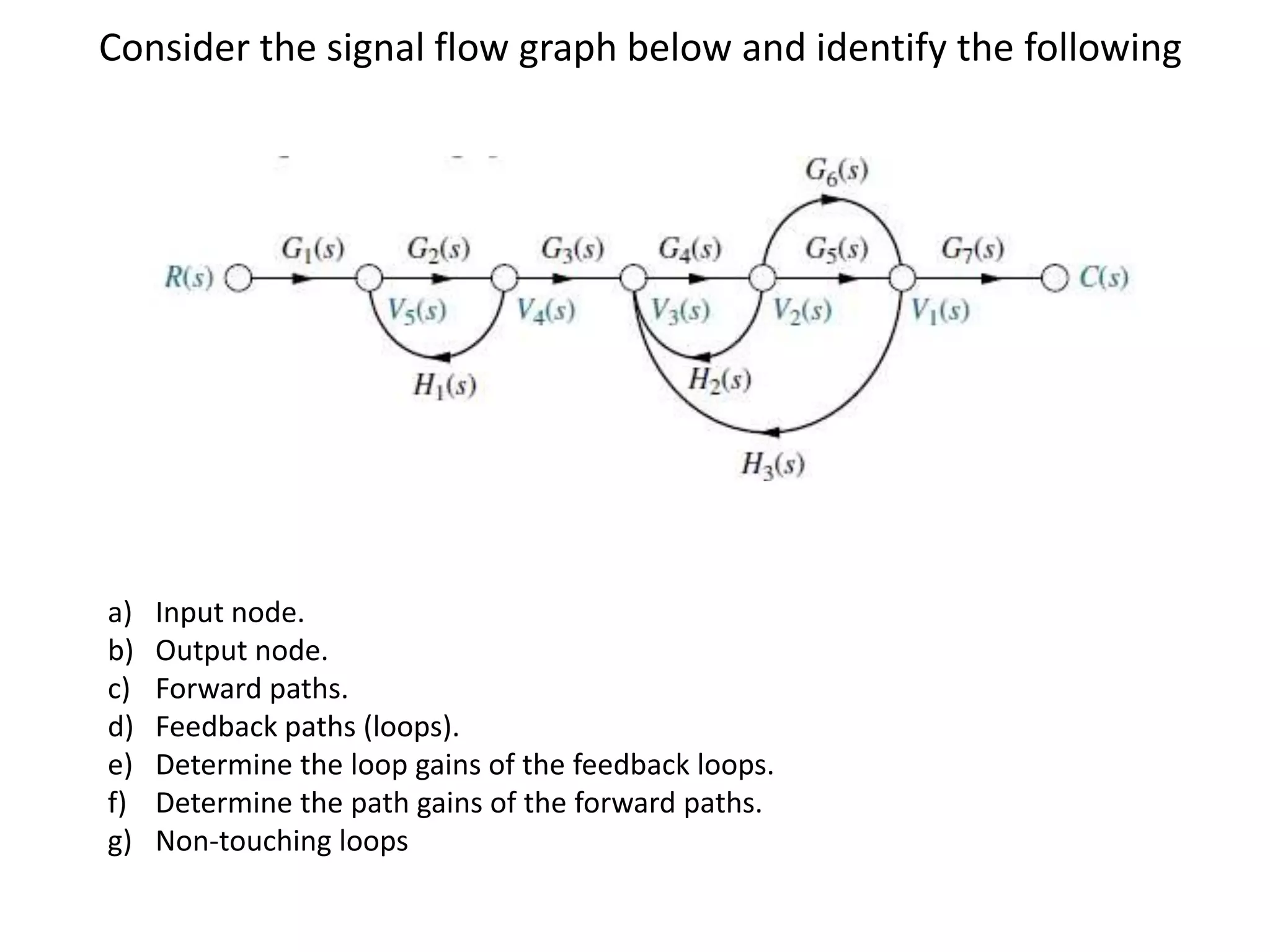
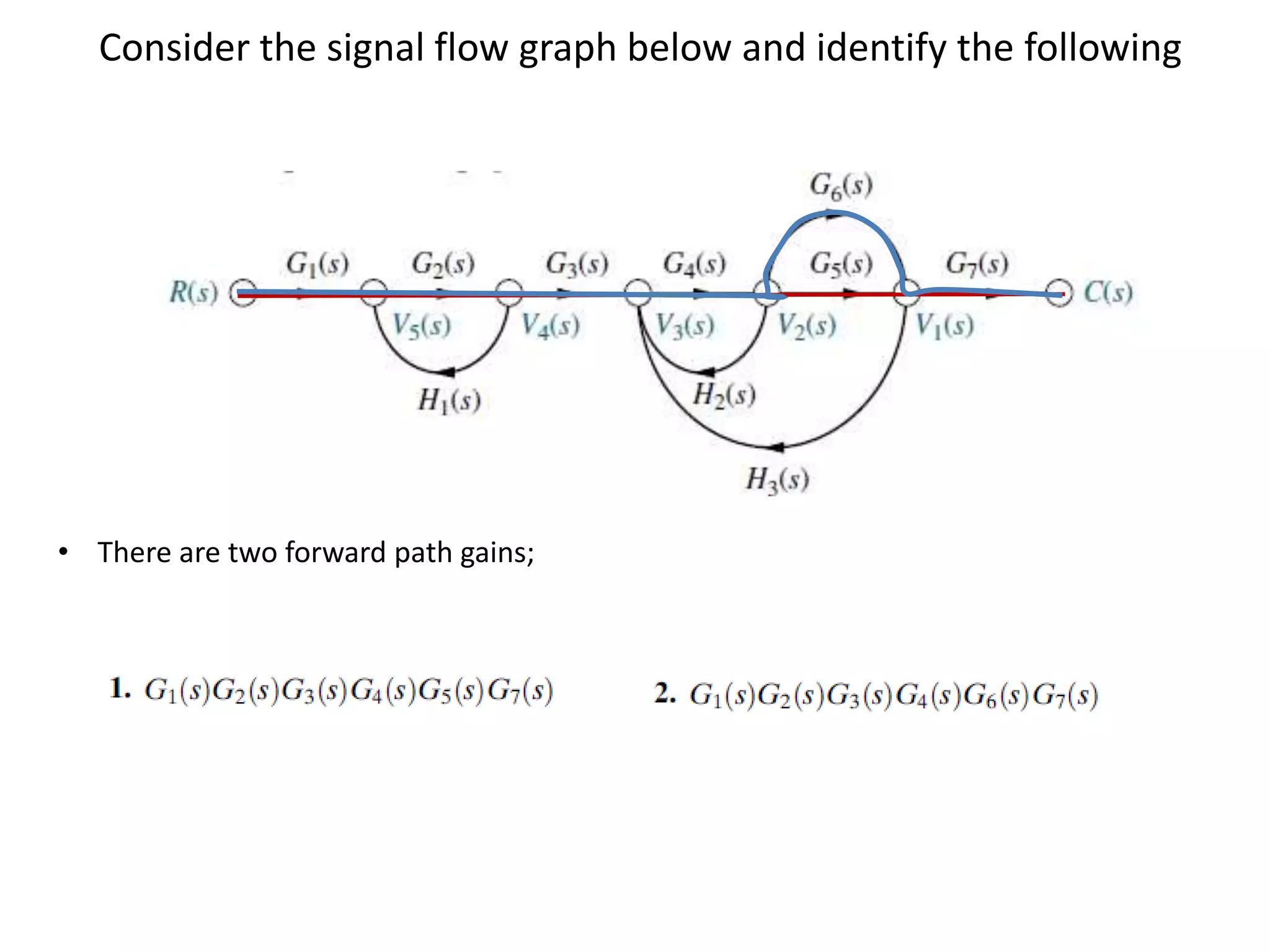
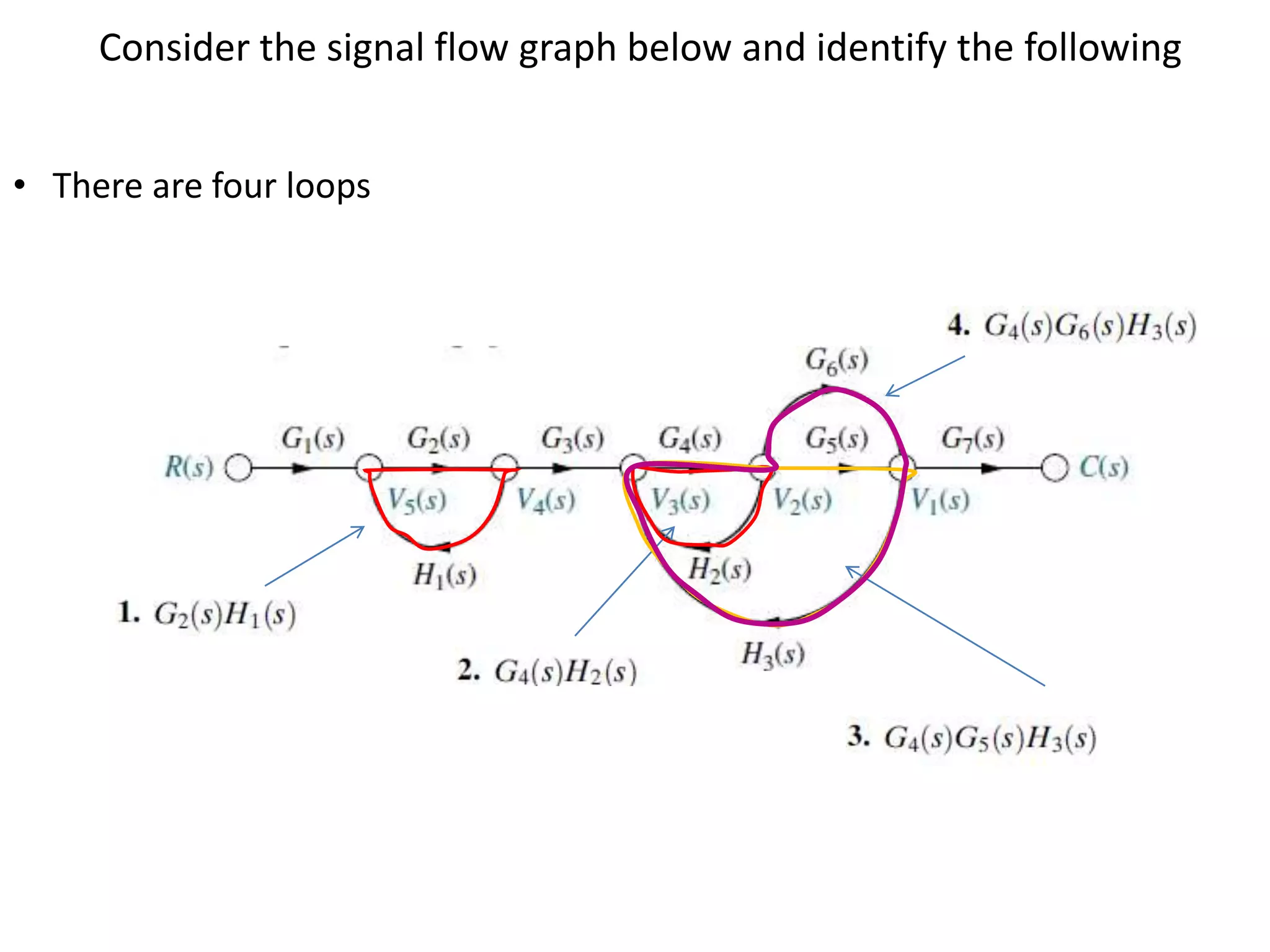
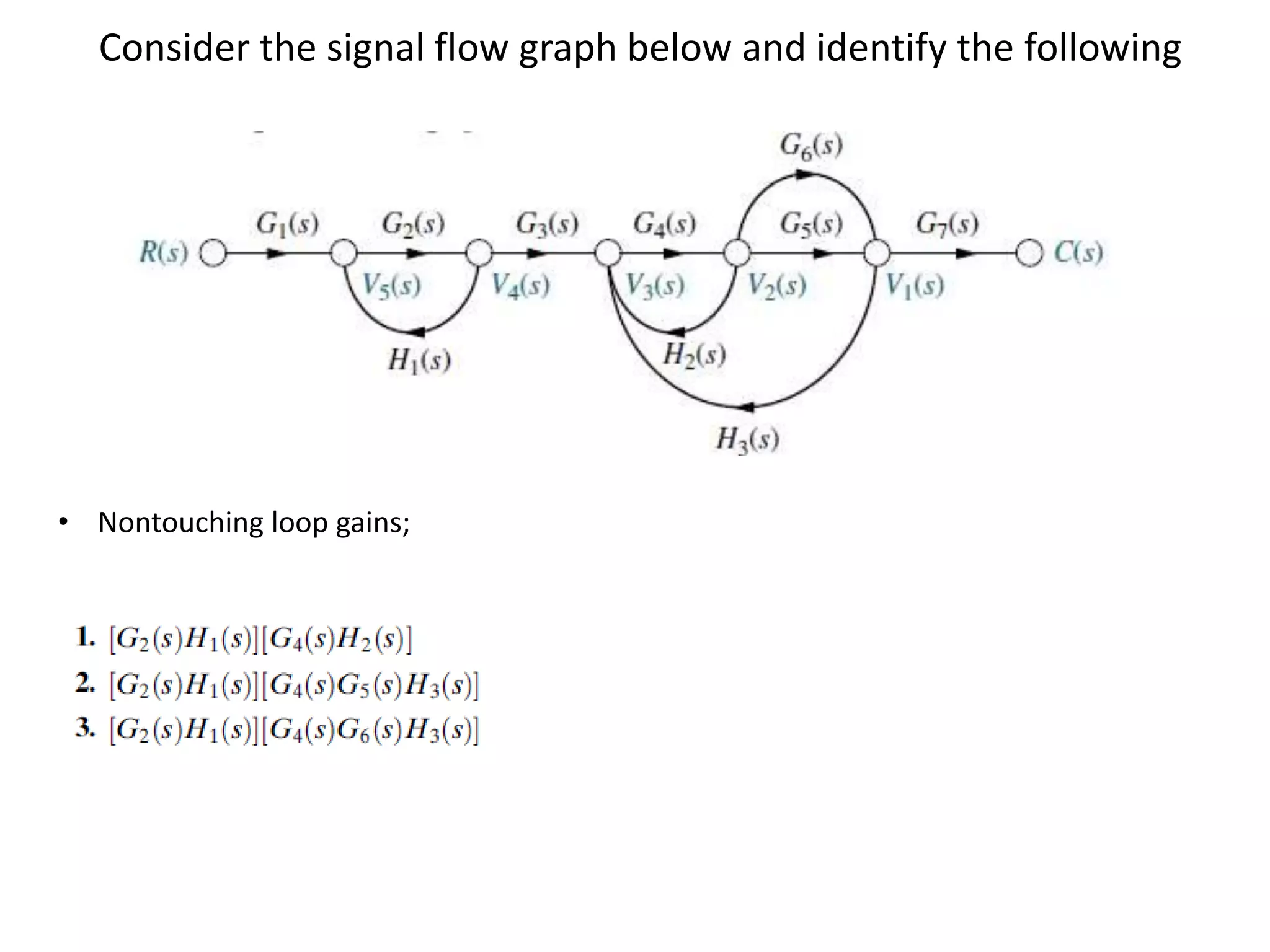
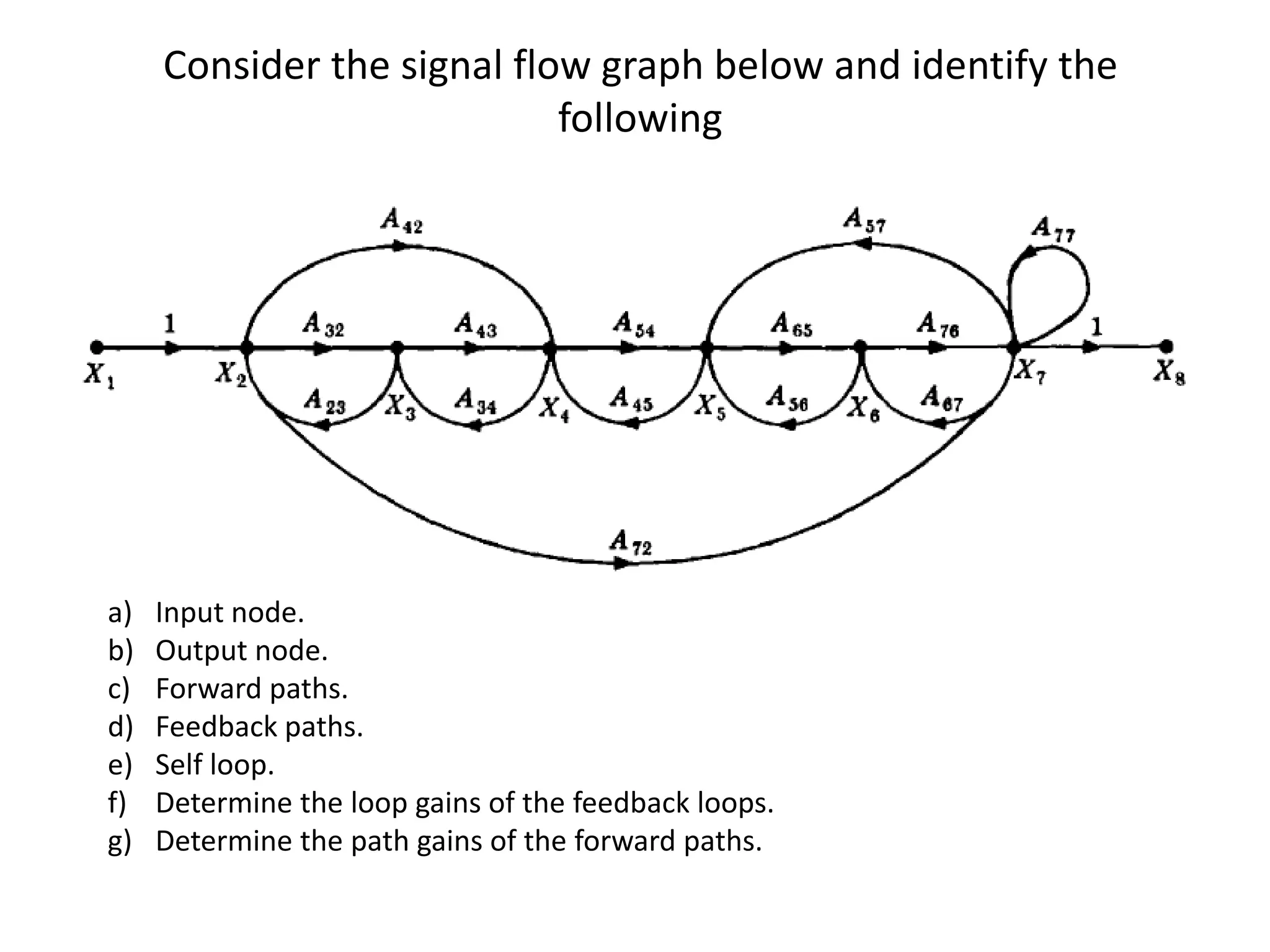
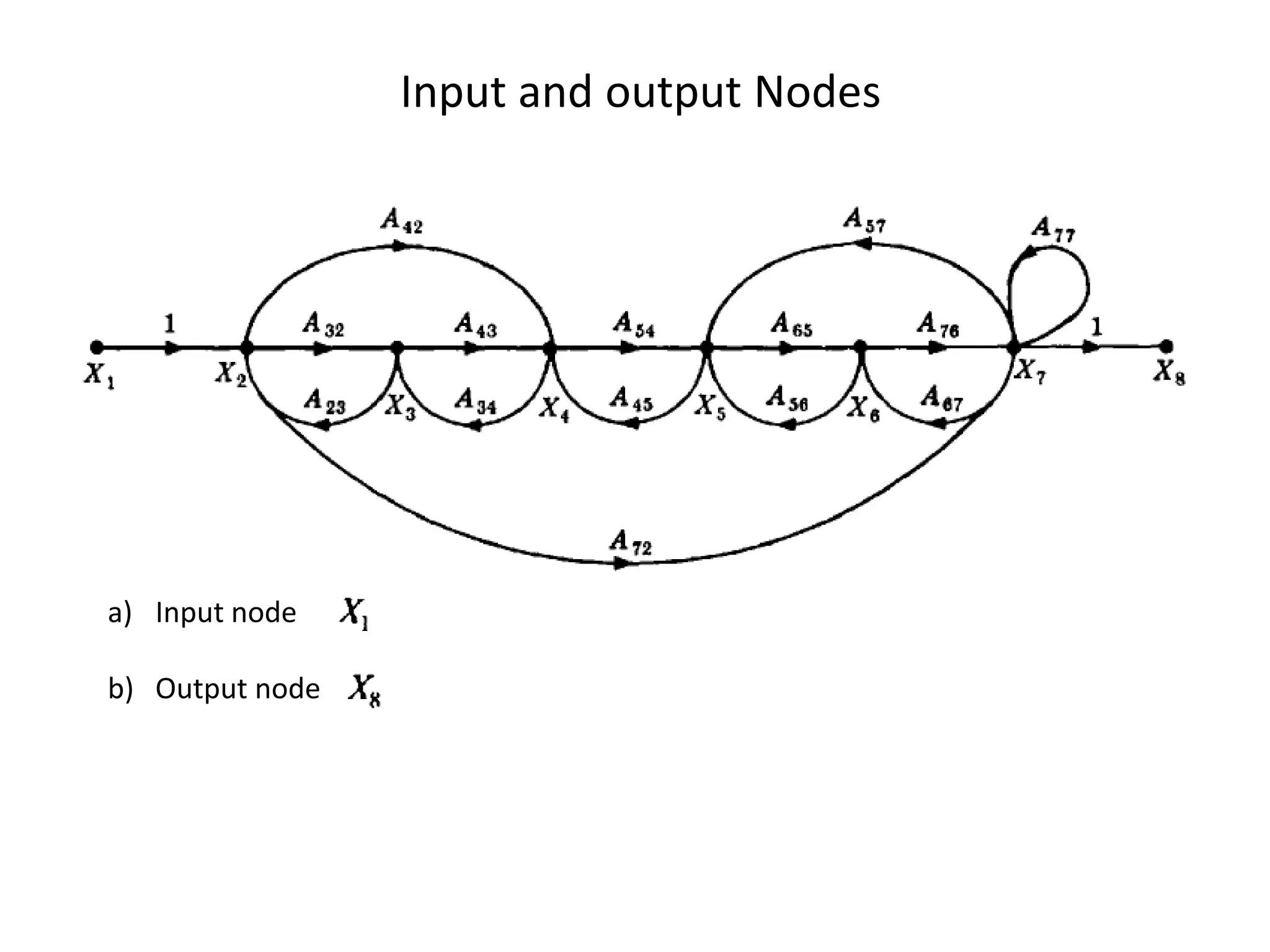
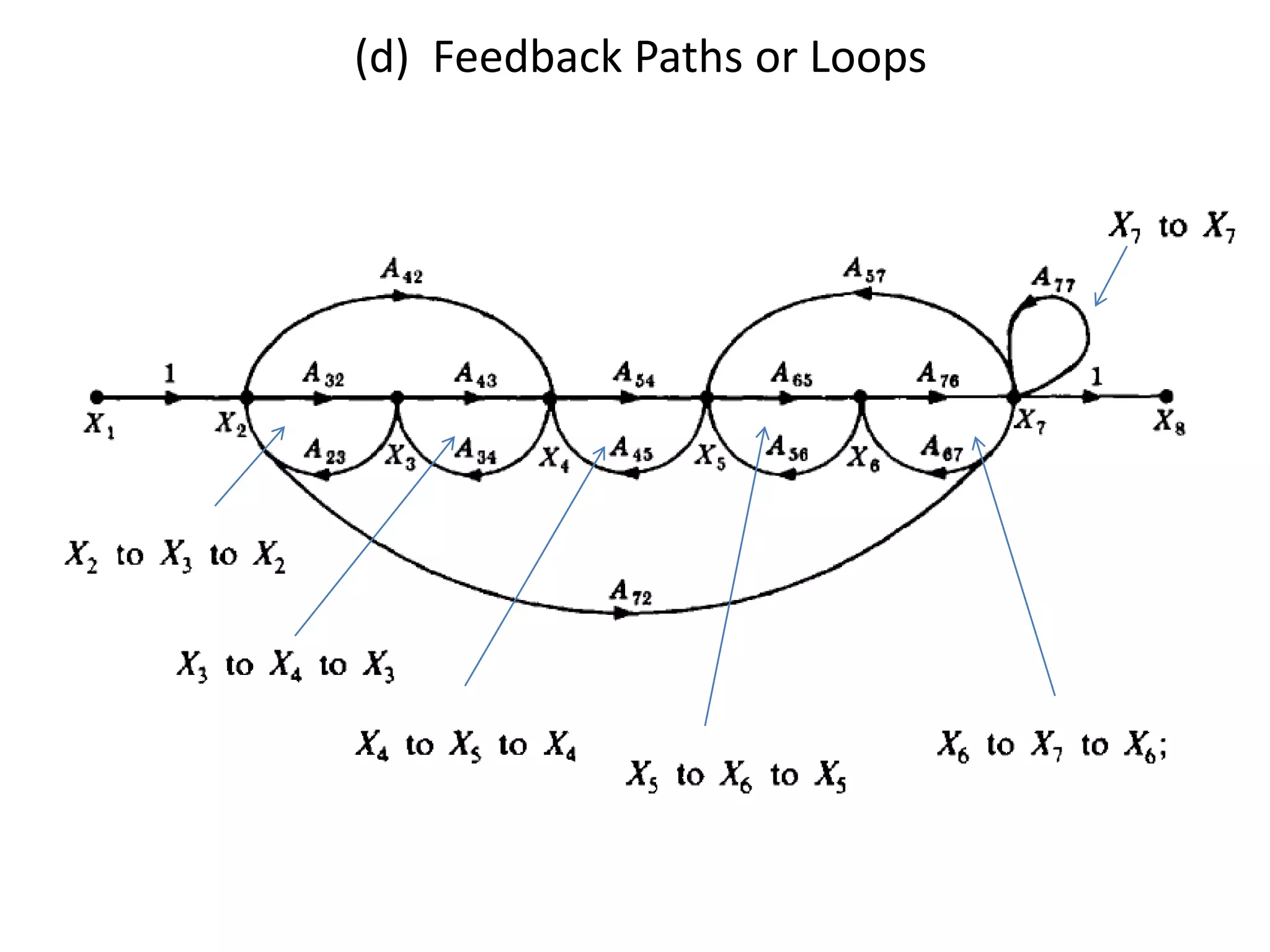
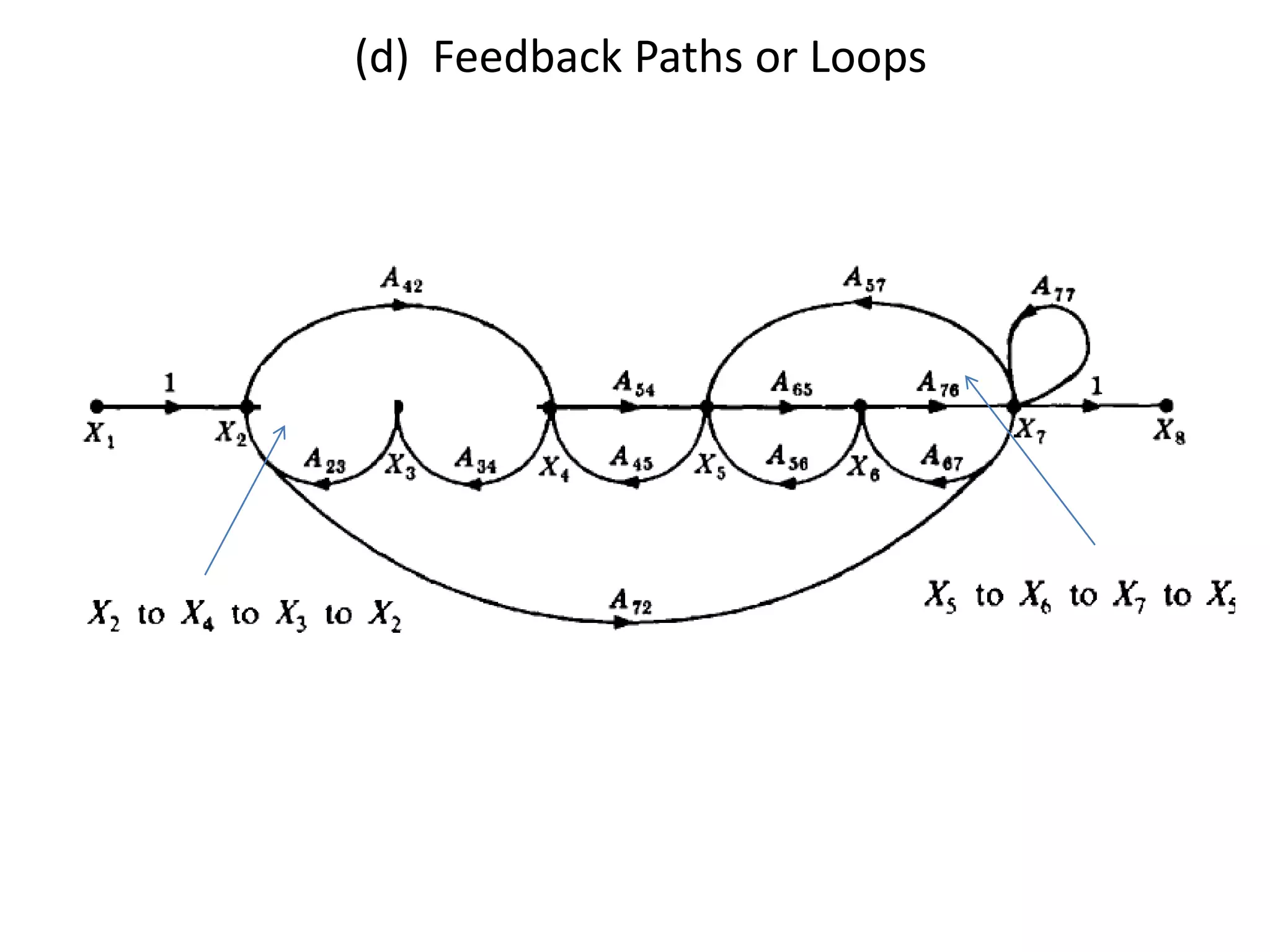
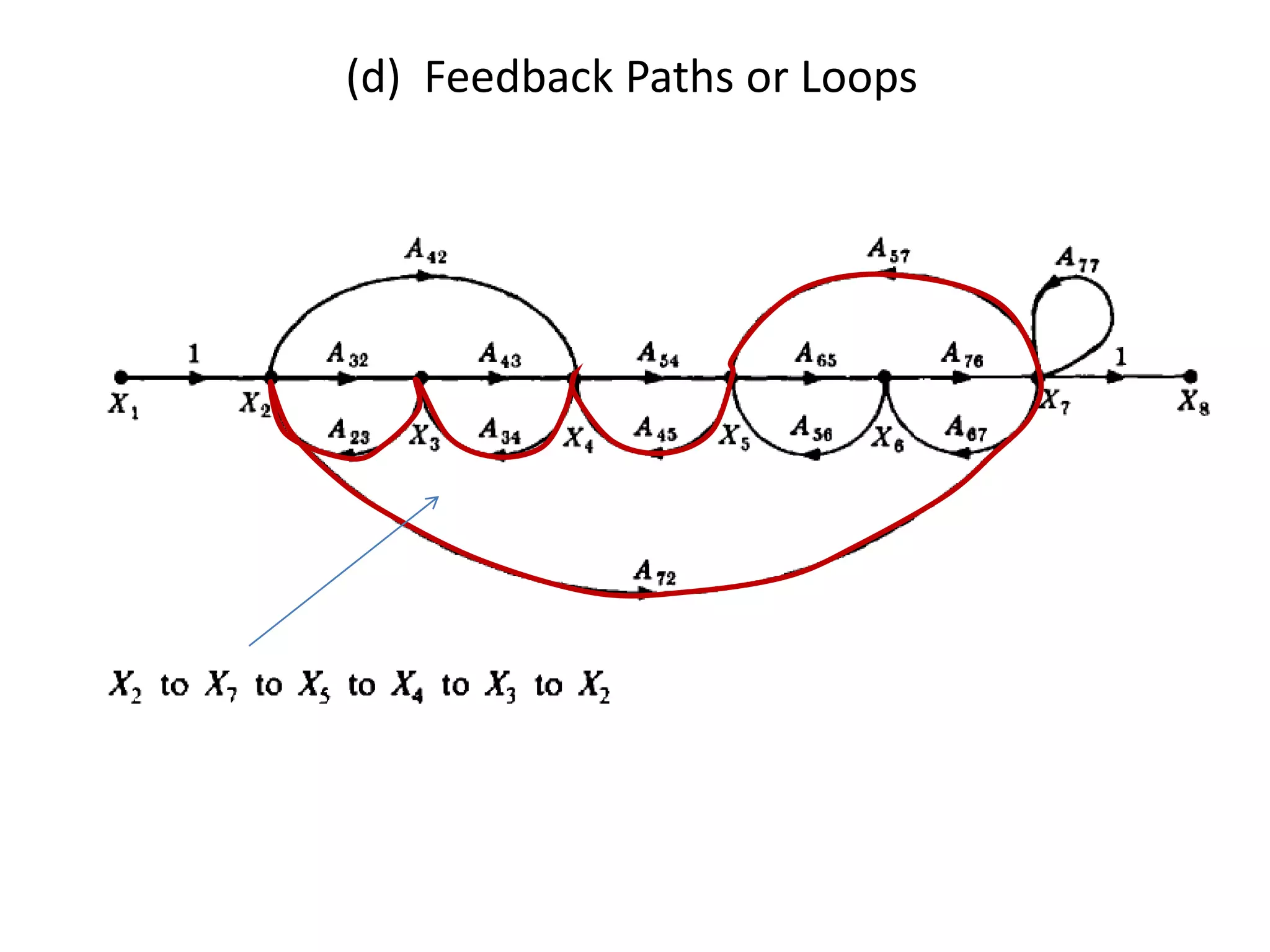
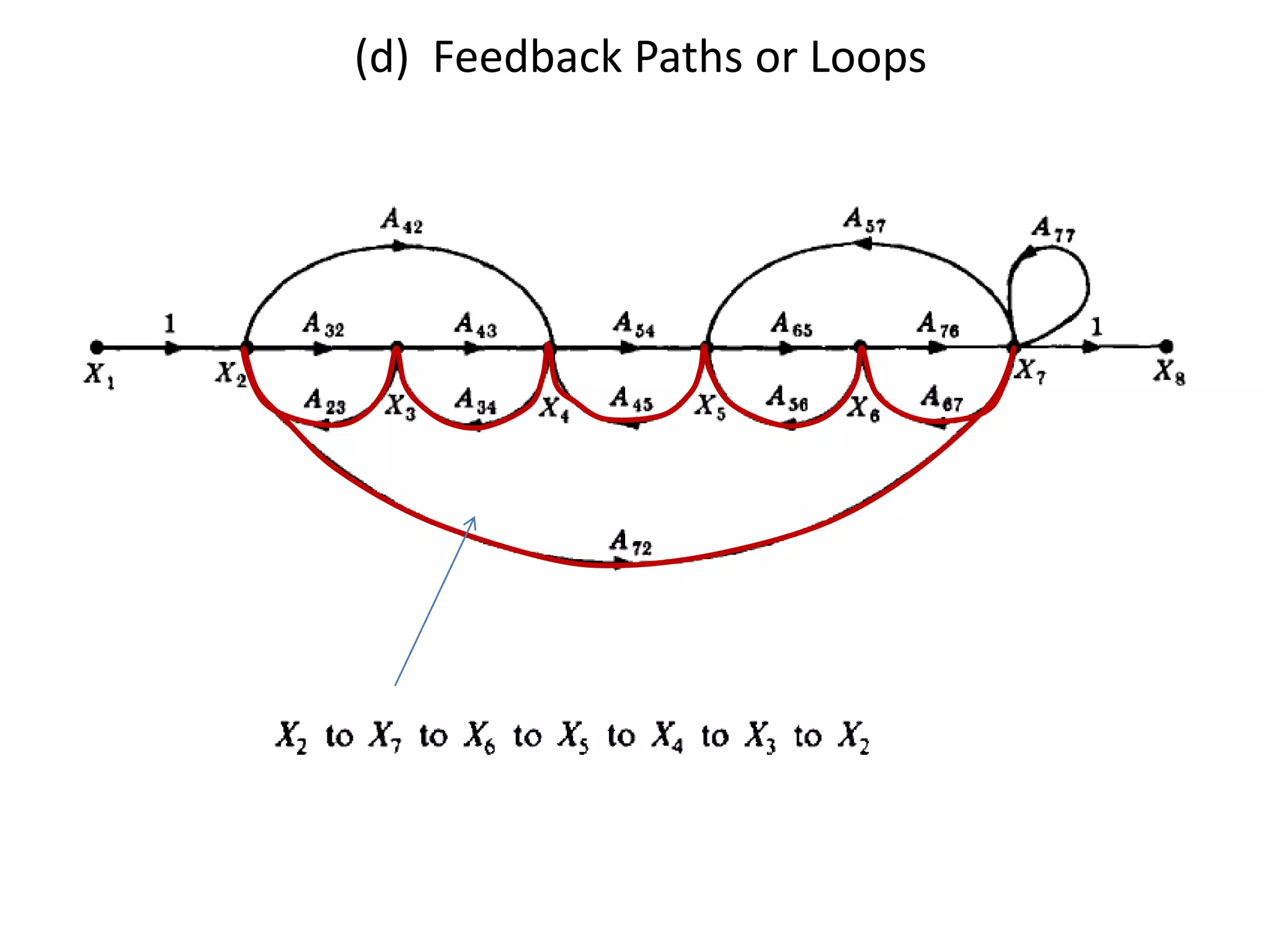
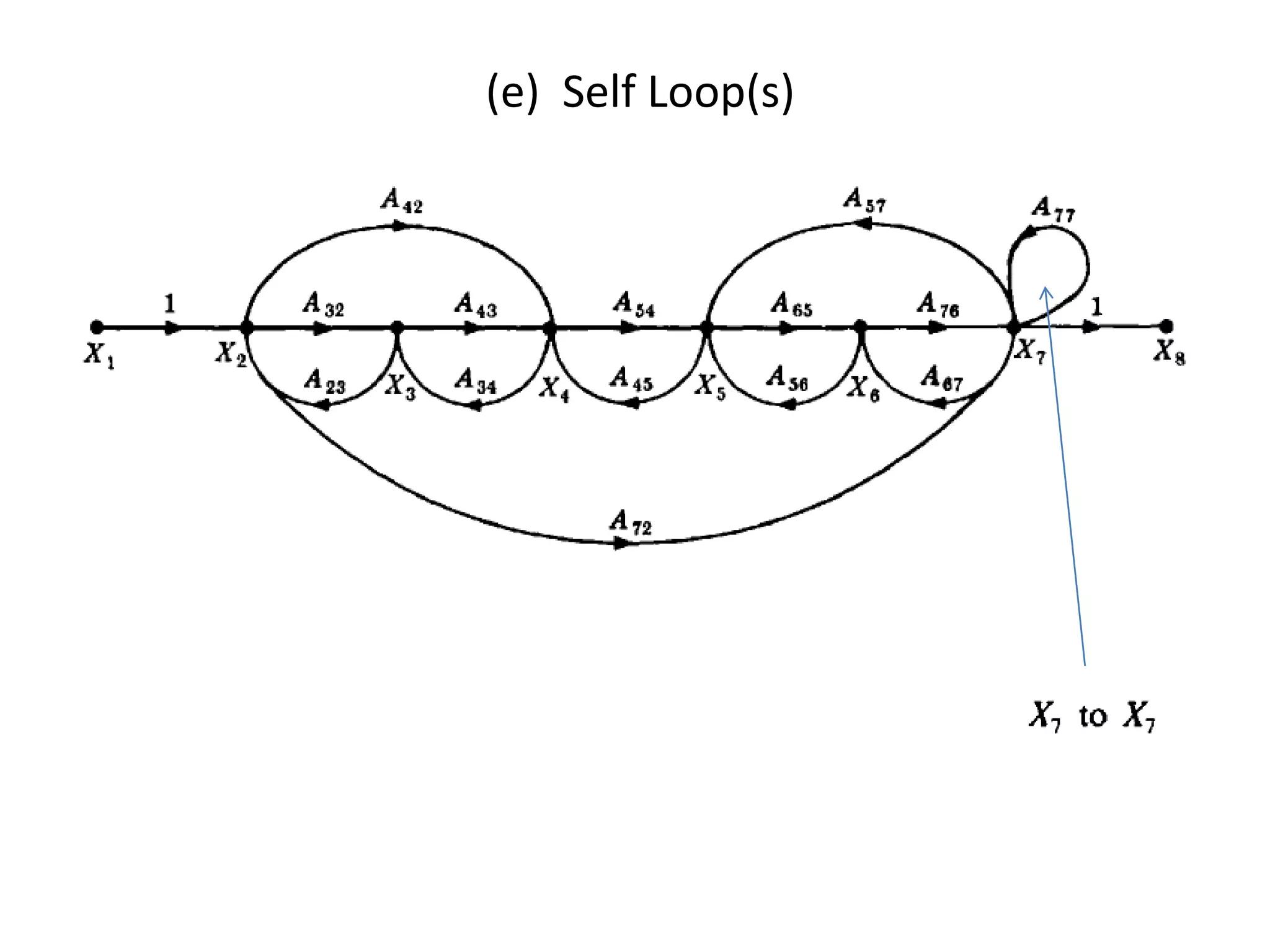
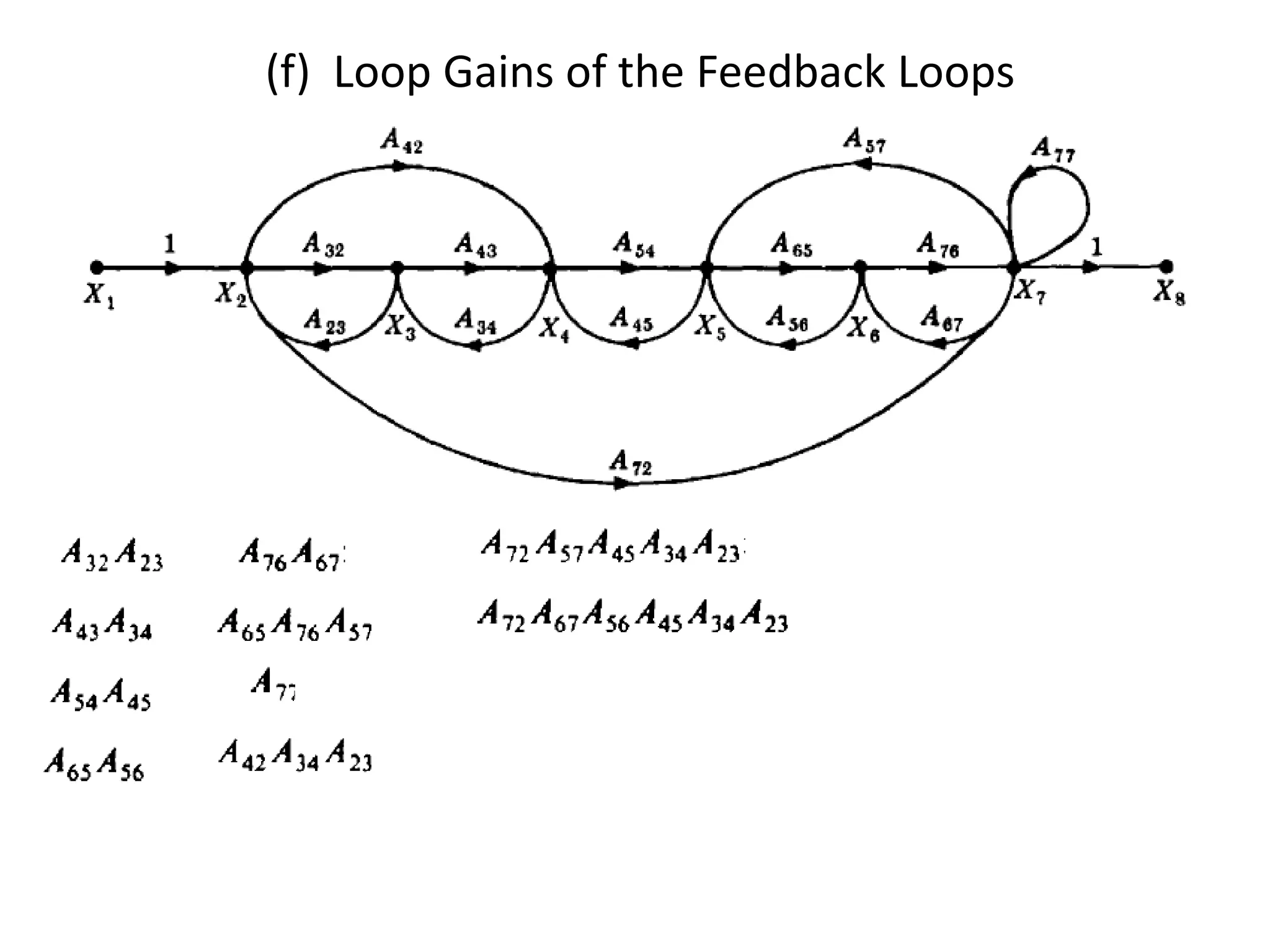
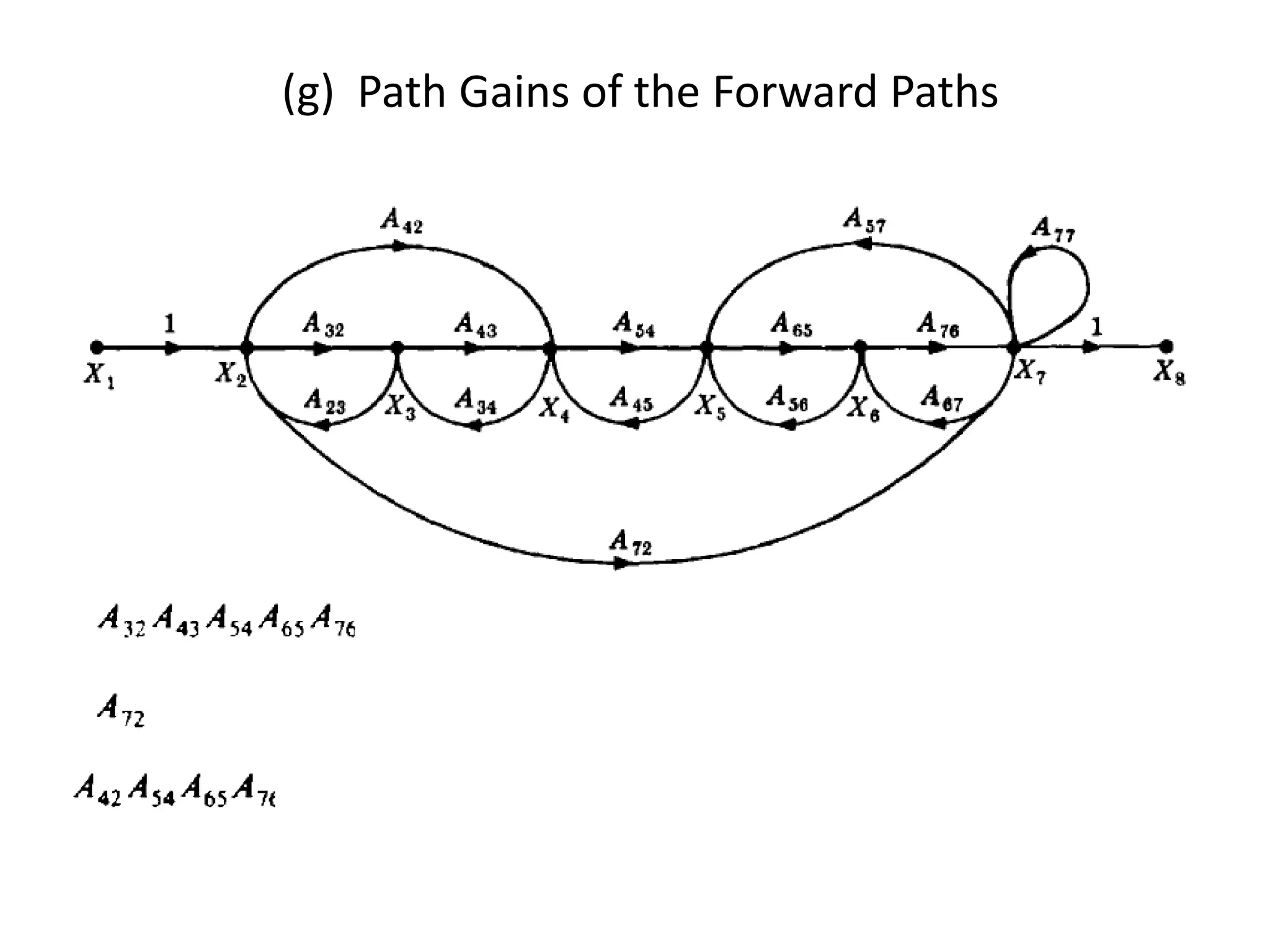
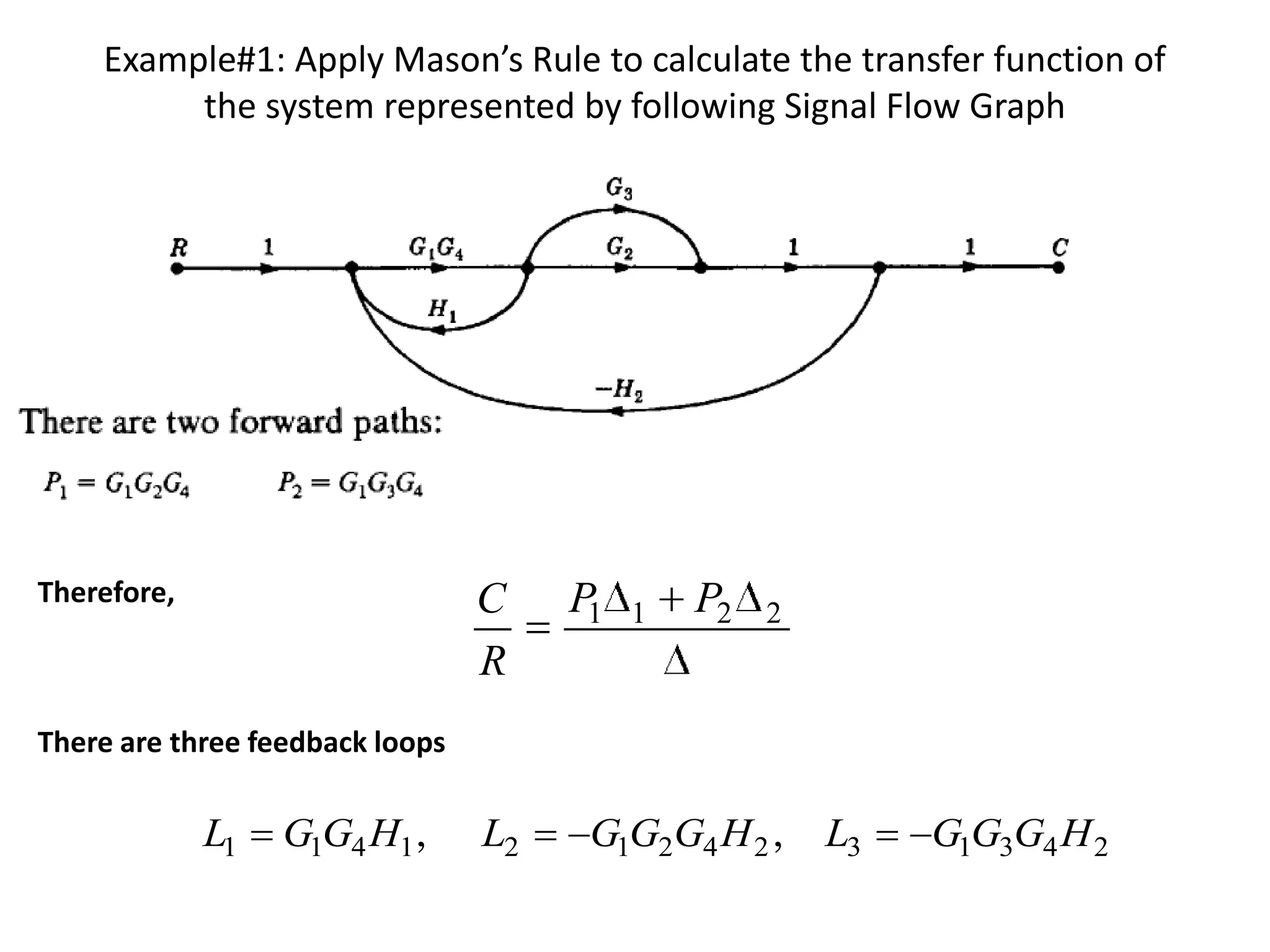
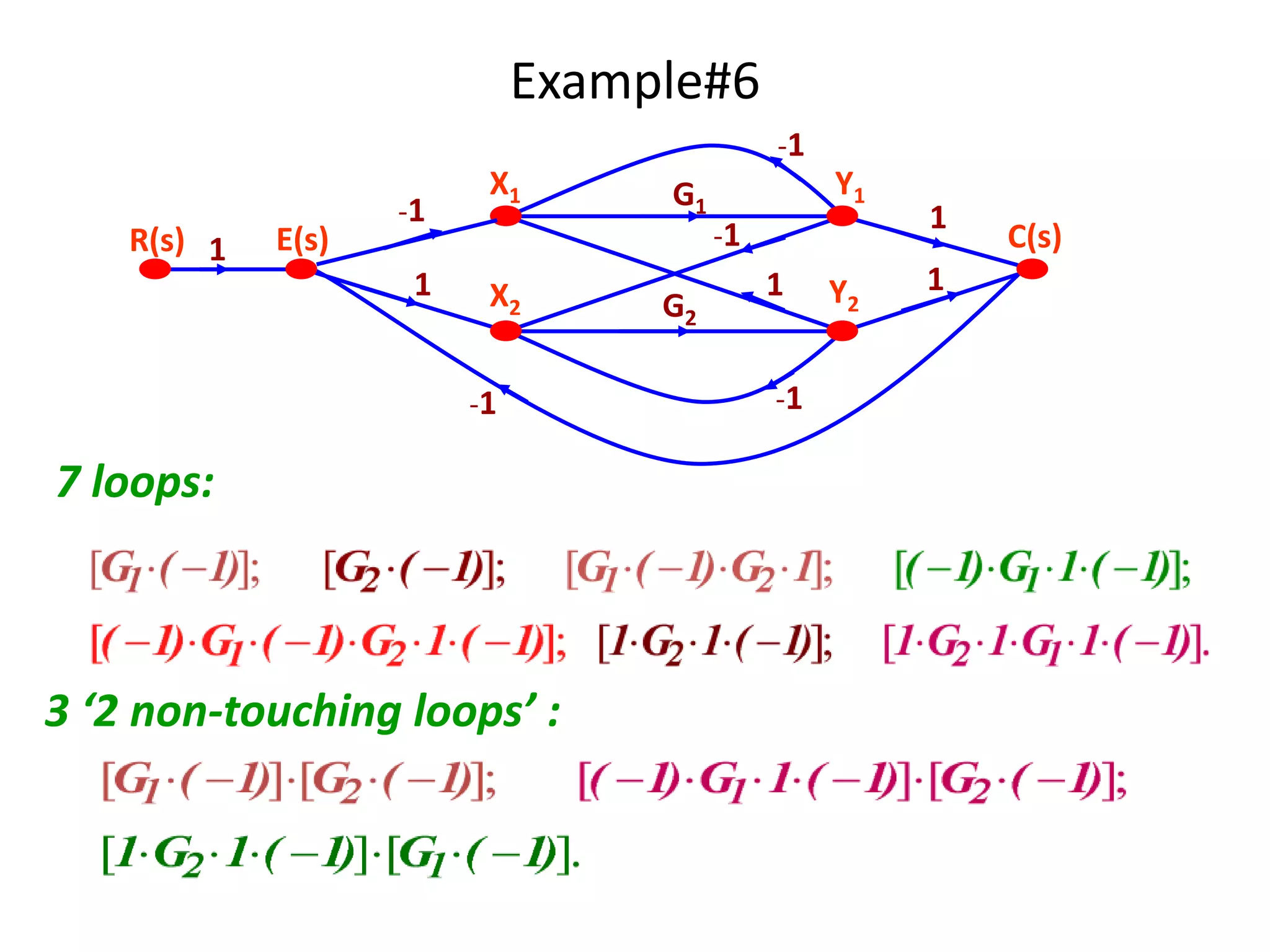
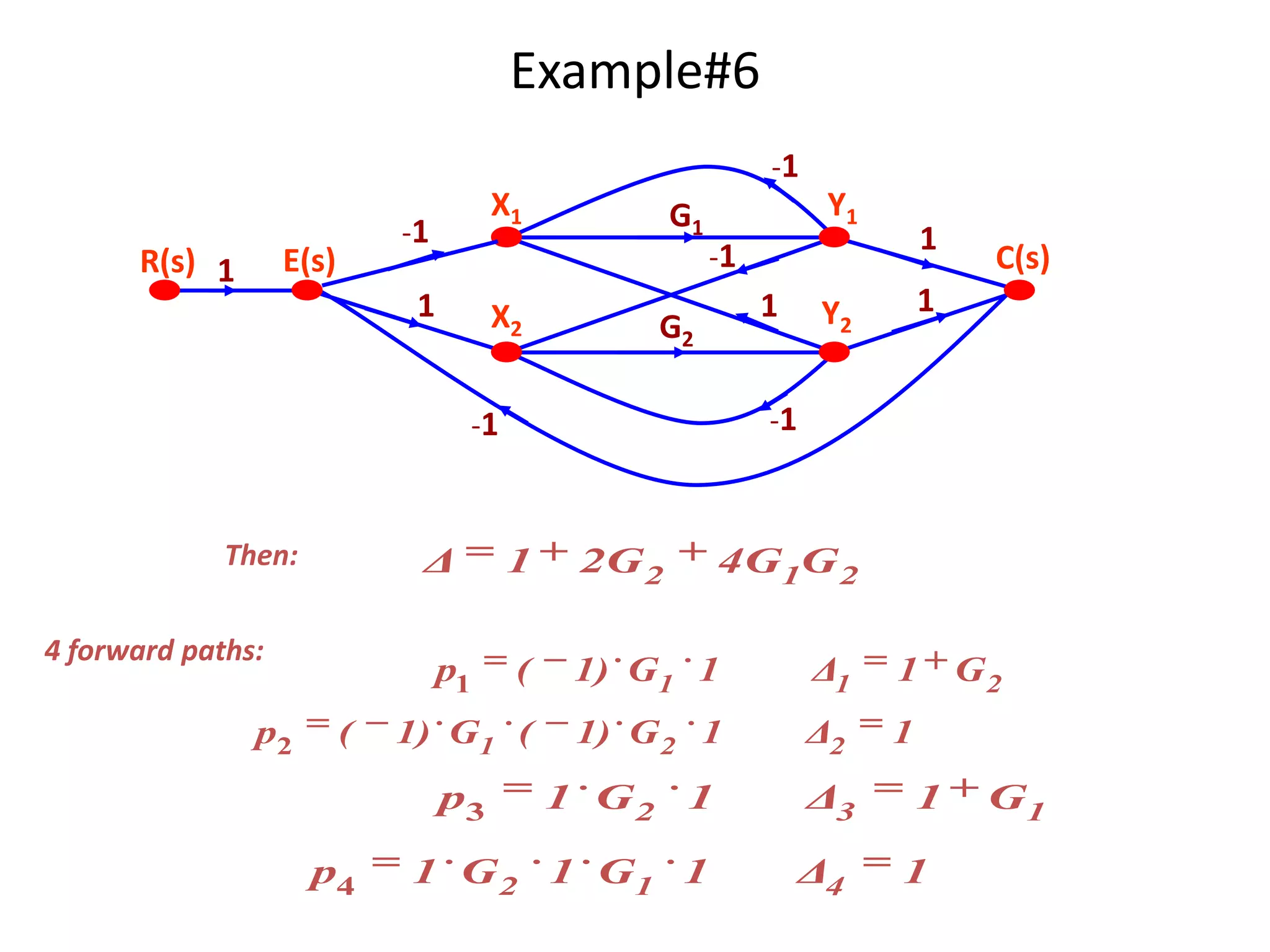
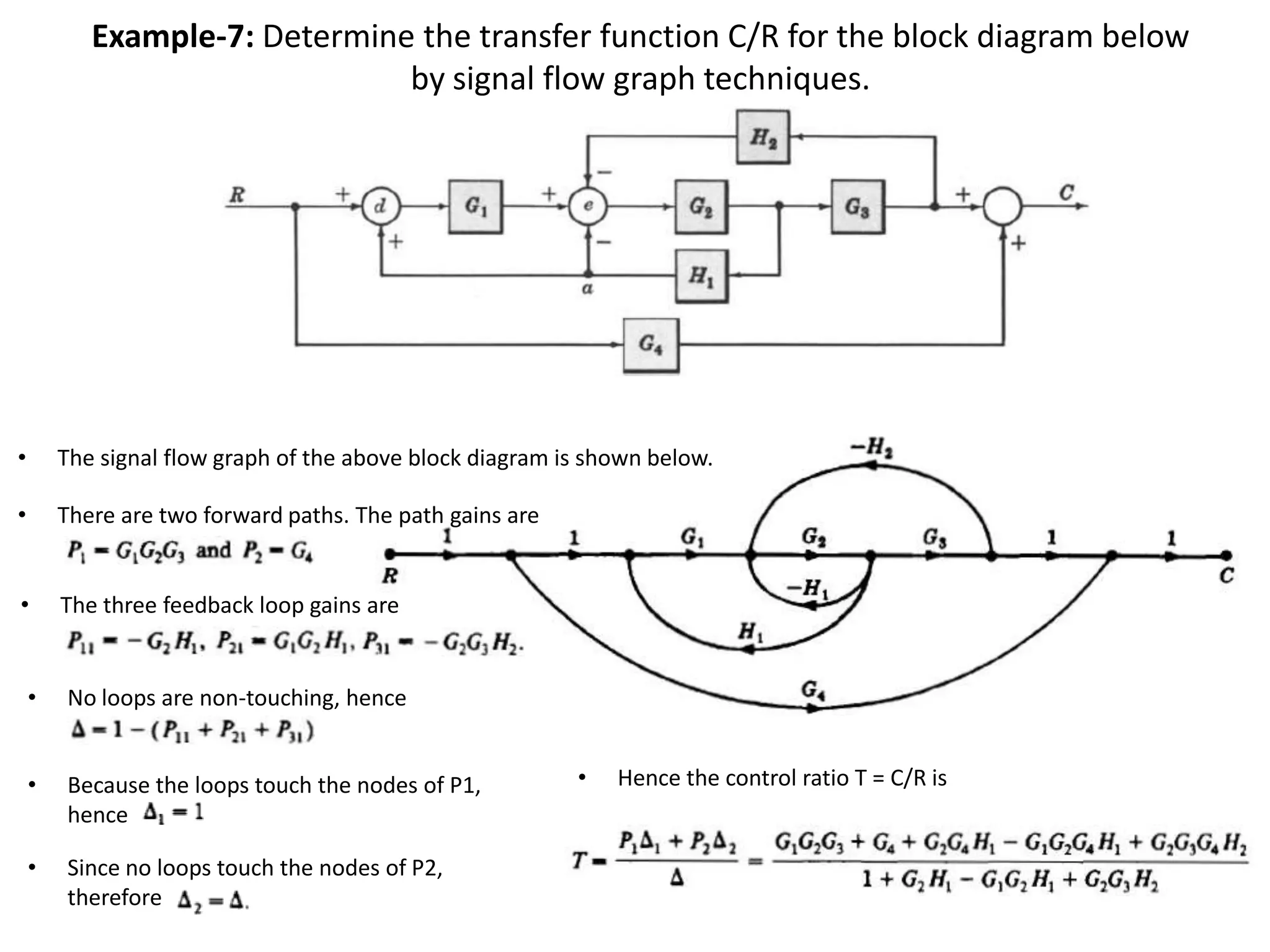
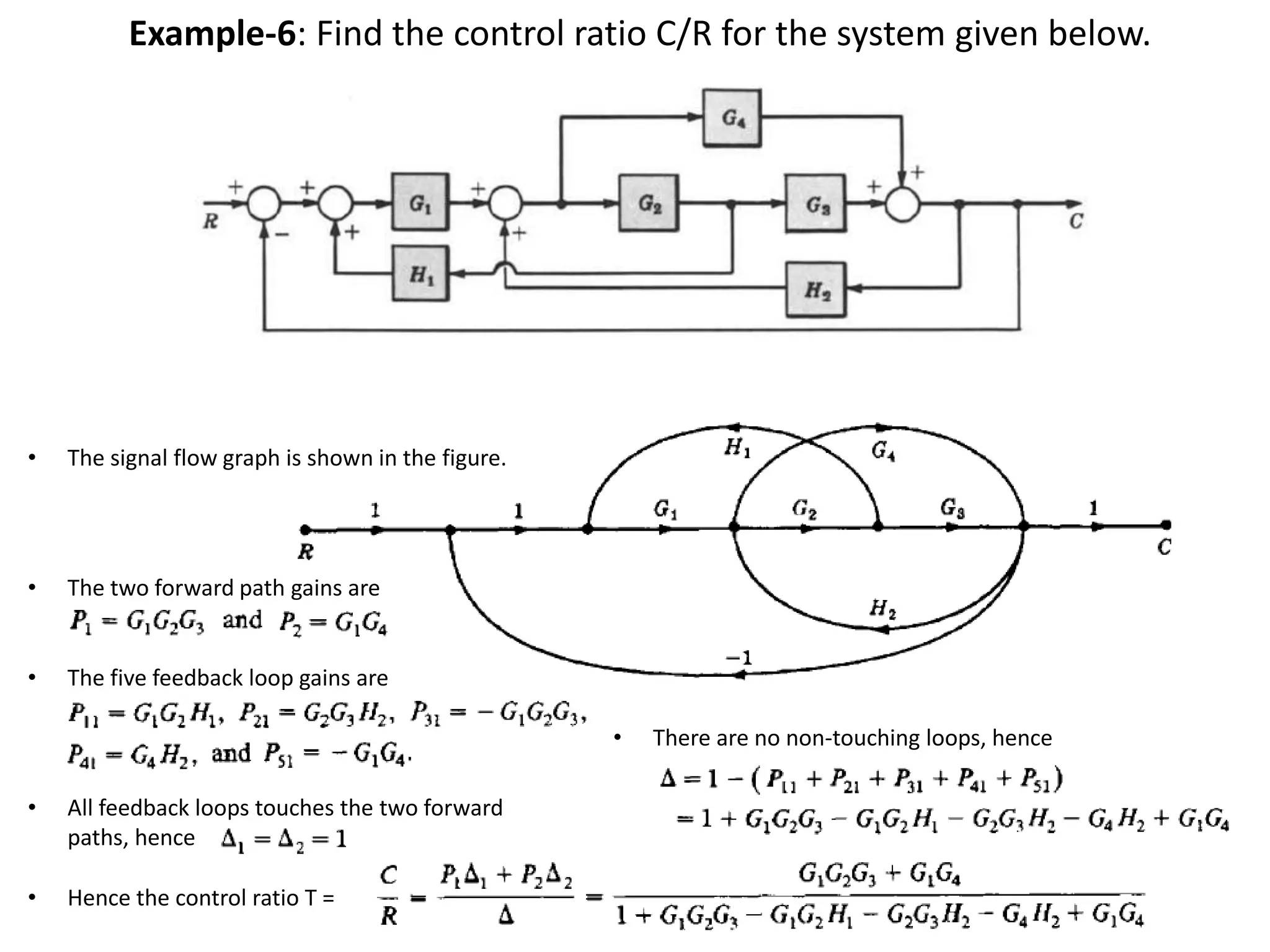
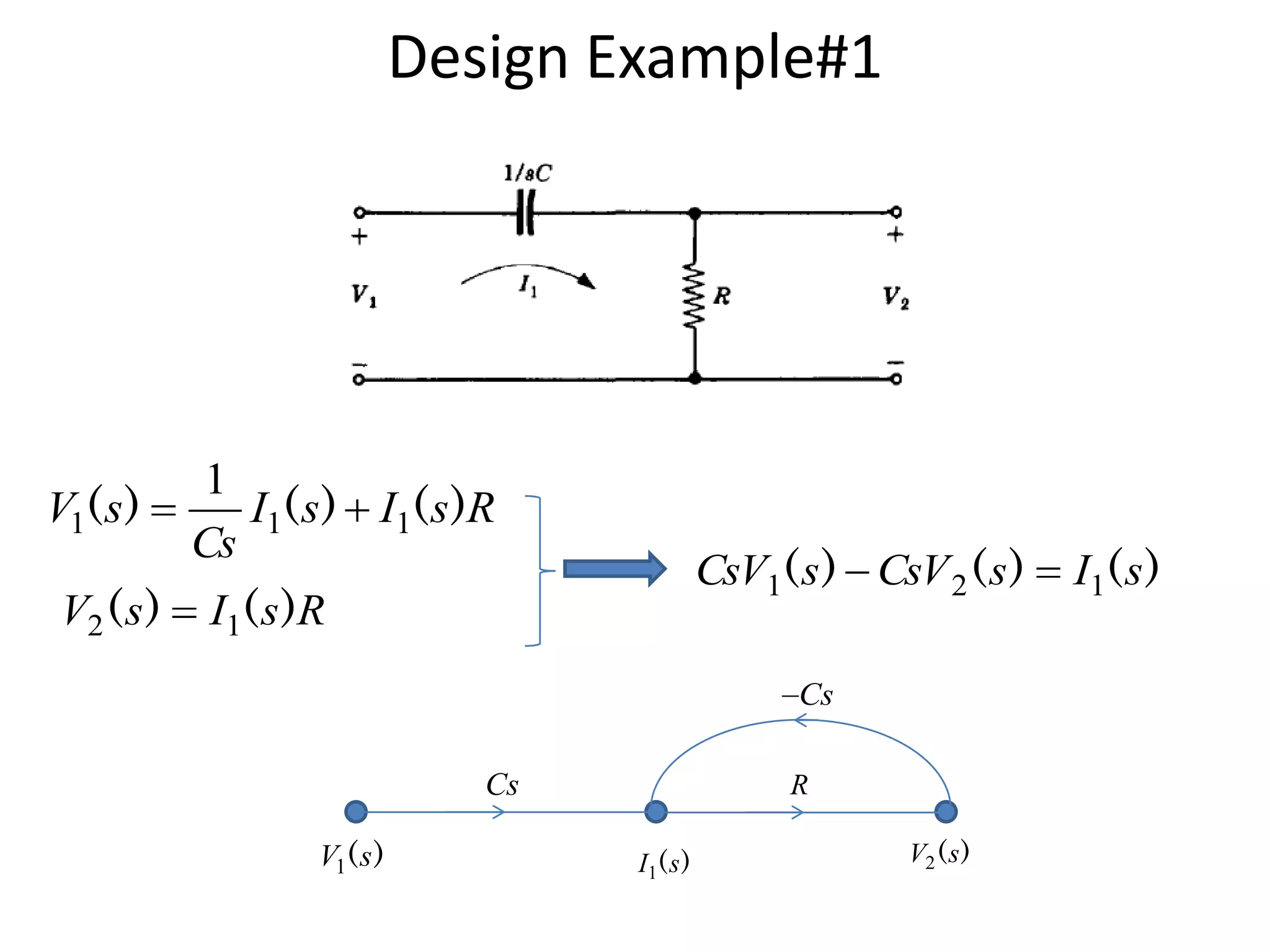
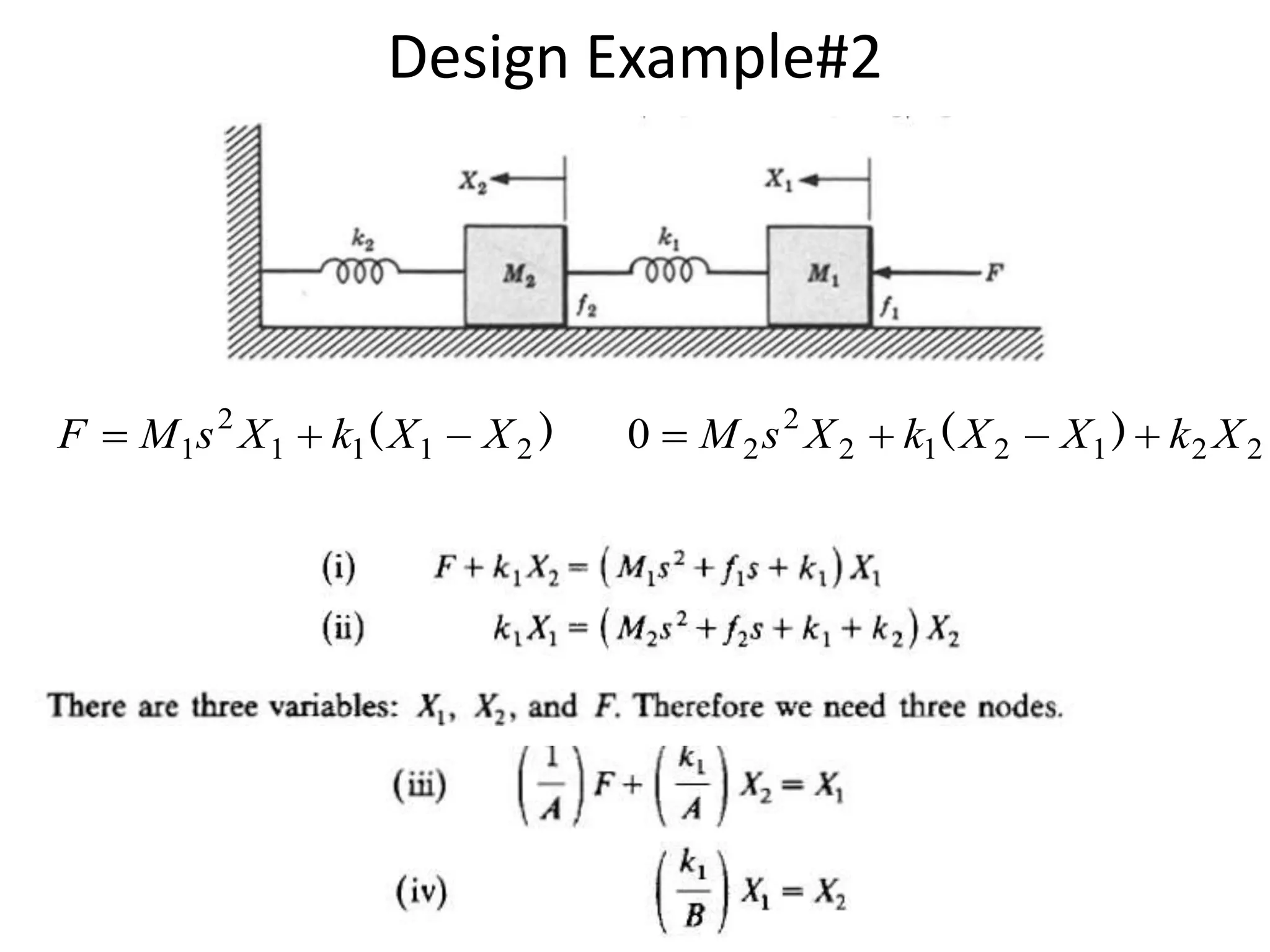
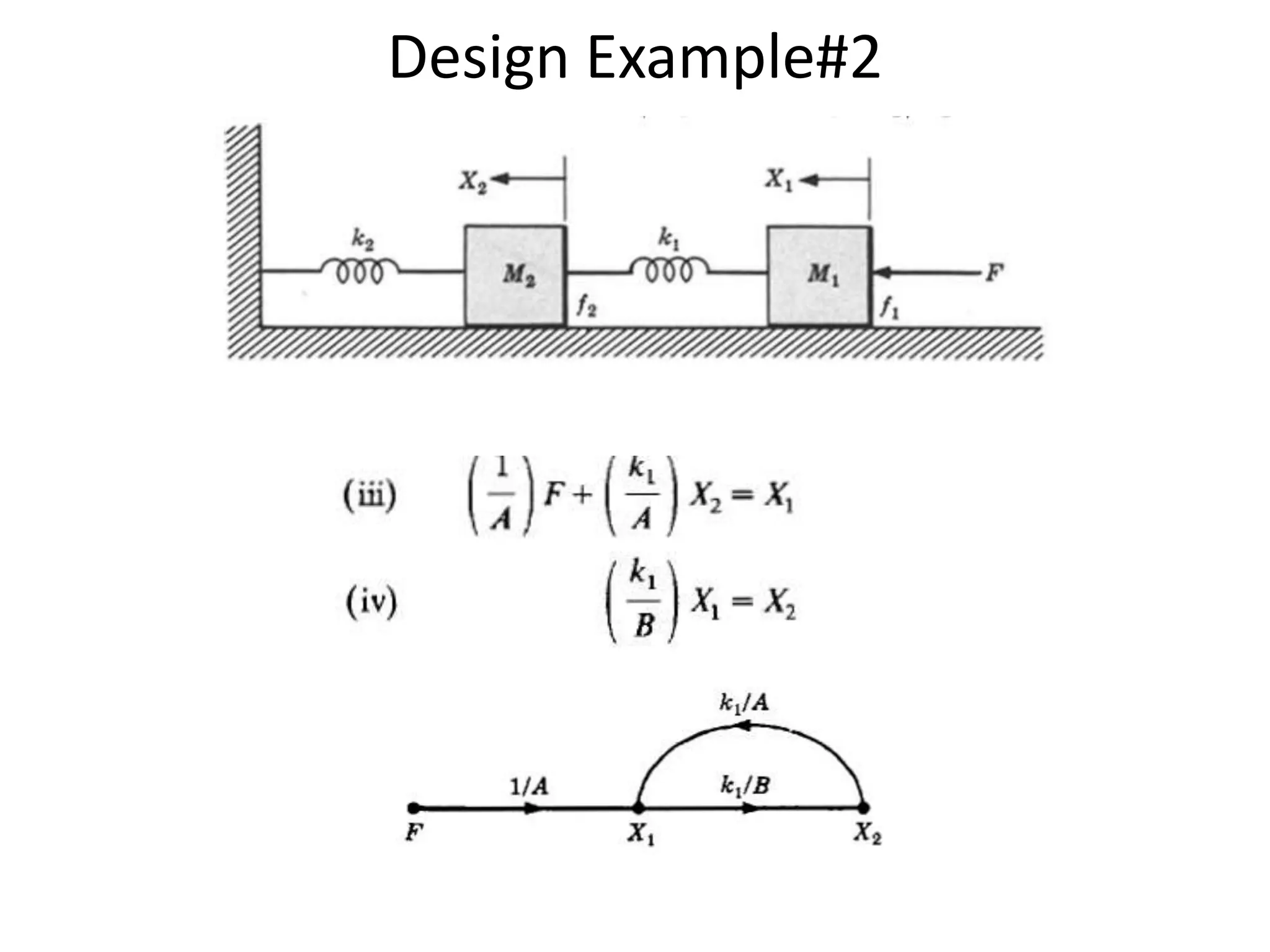
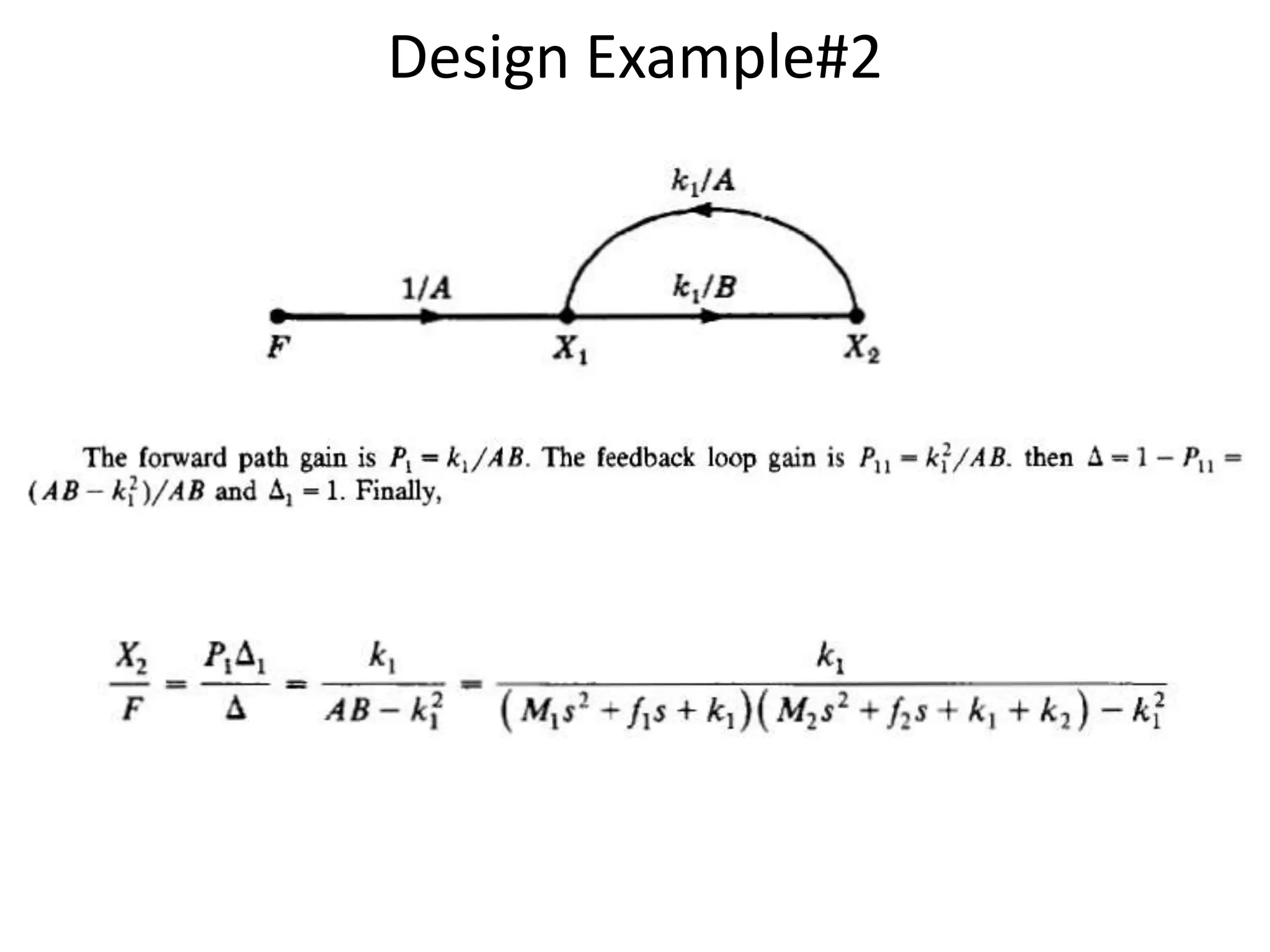
This document provides an overview of signal flow graphs including:
- Definitions and terminology of signal flow graphs
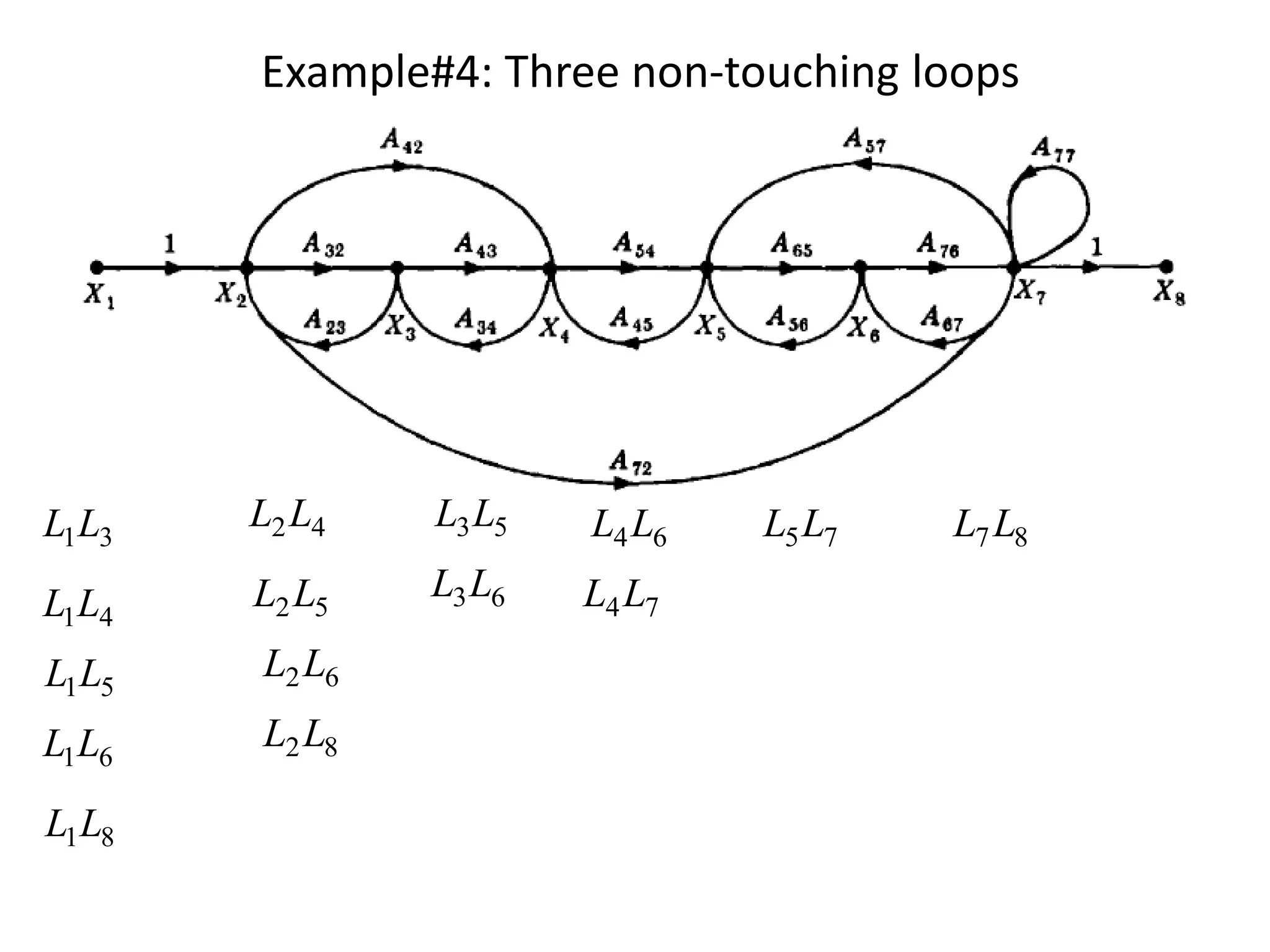
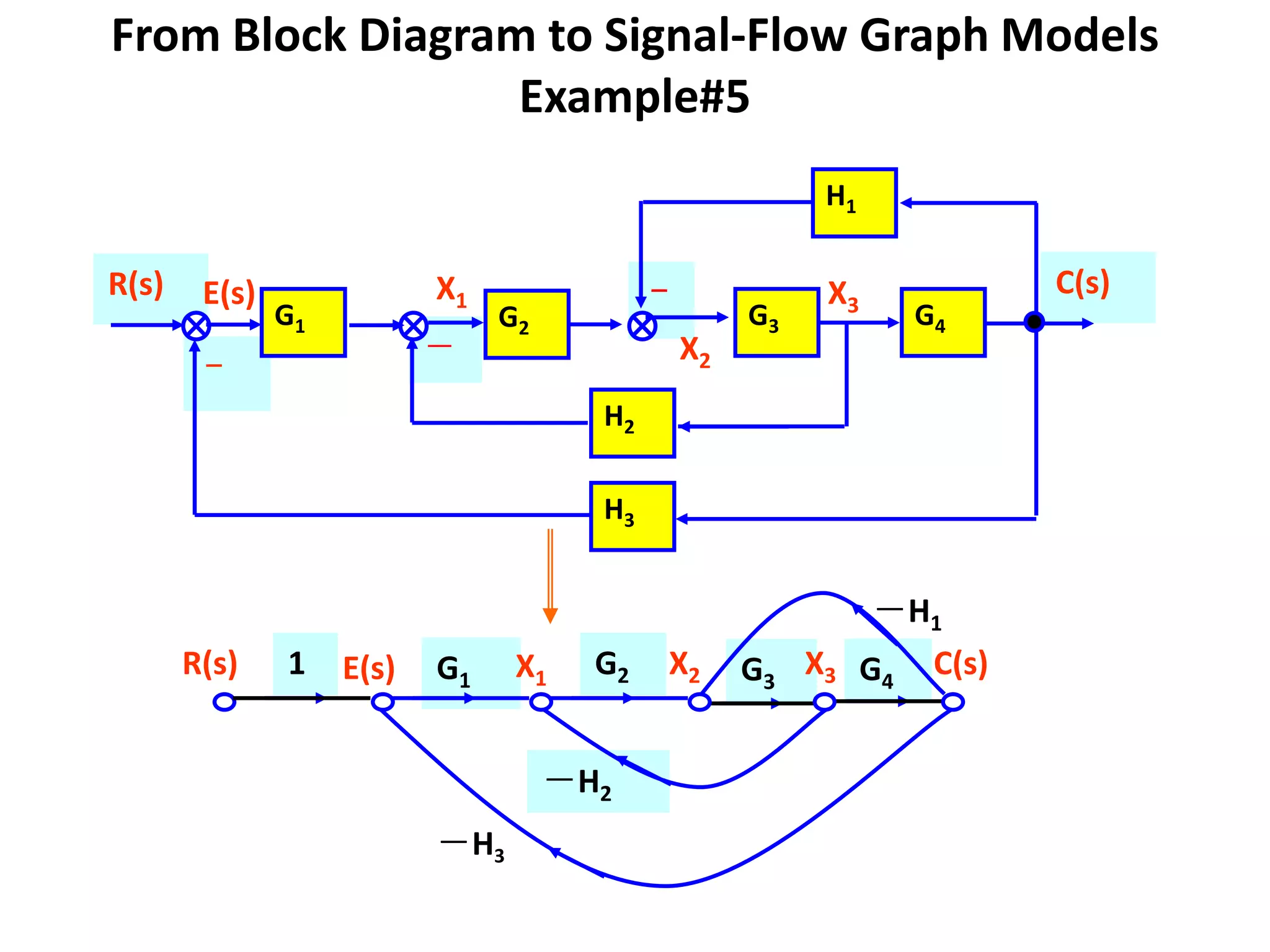
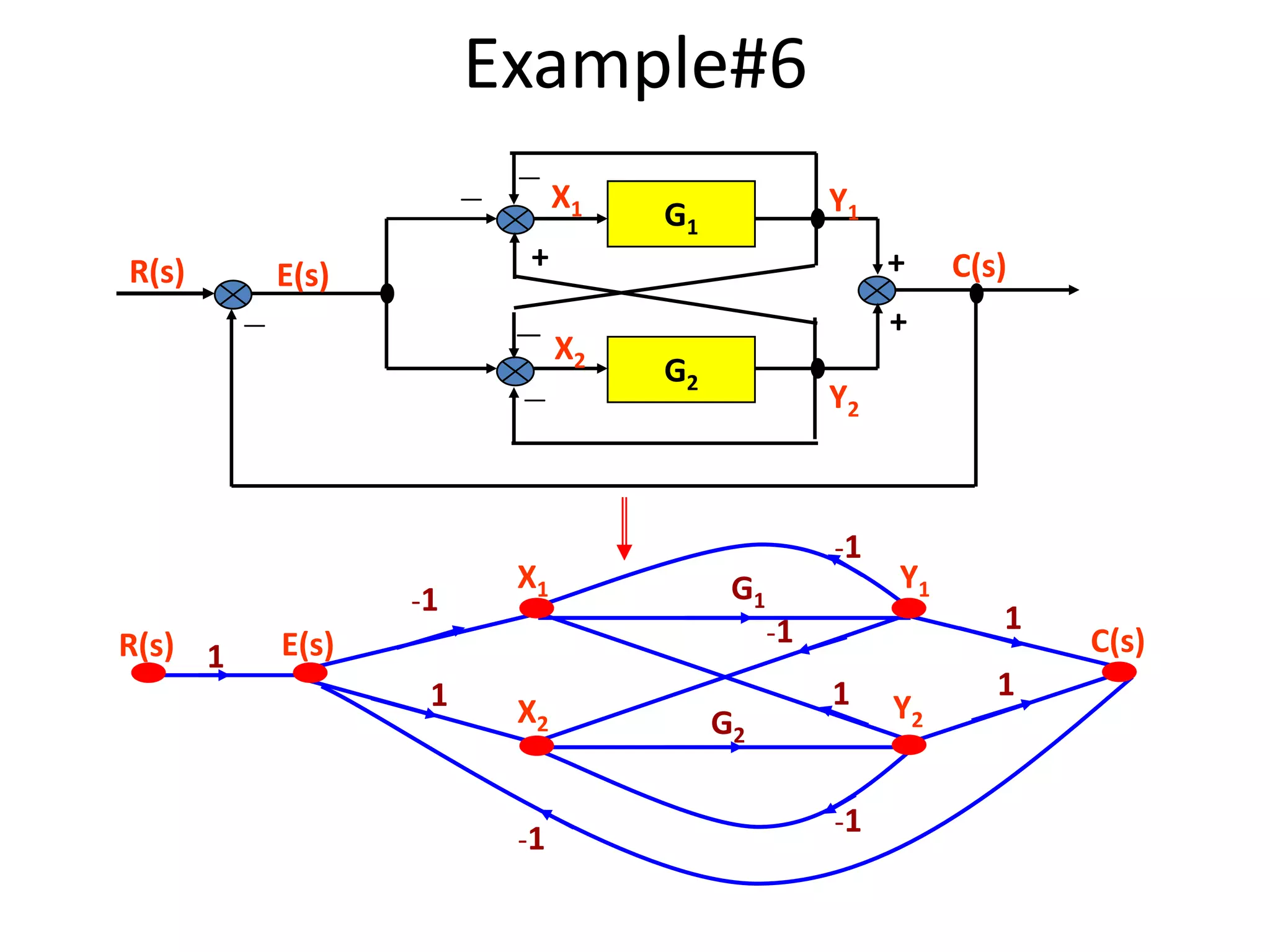
- Examples of constructing signal flow graphs from equations and block diagrams
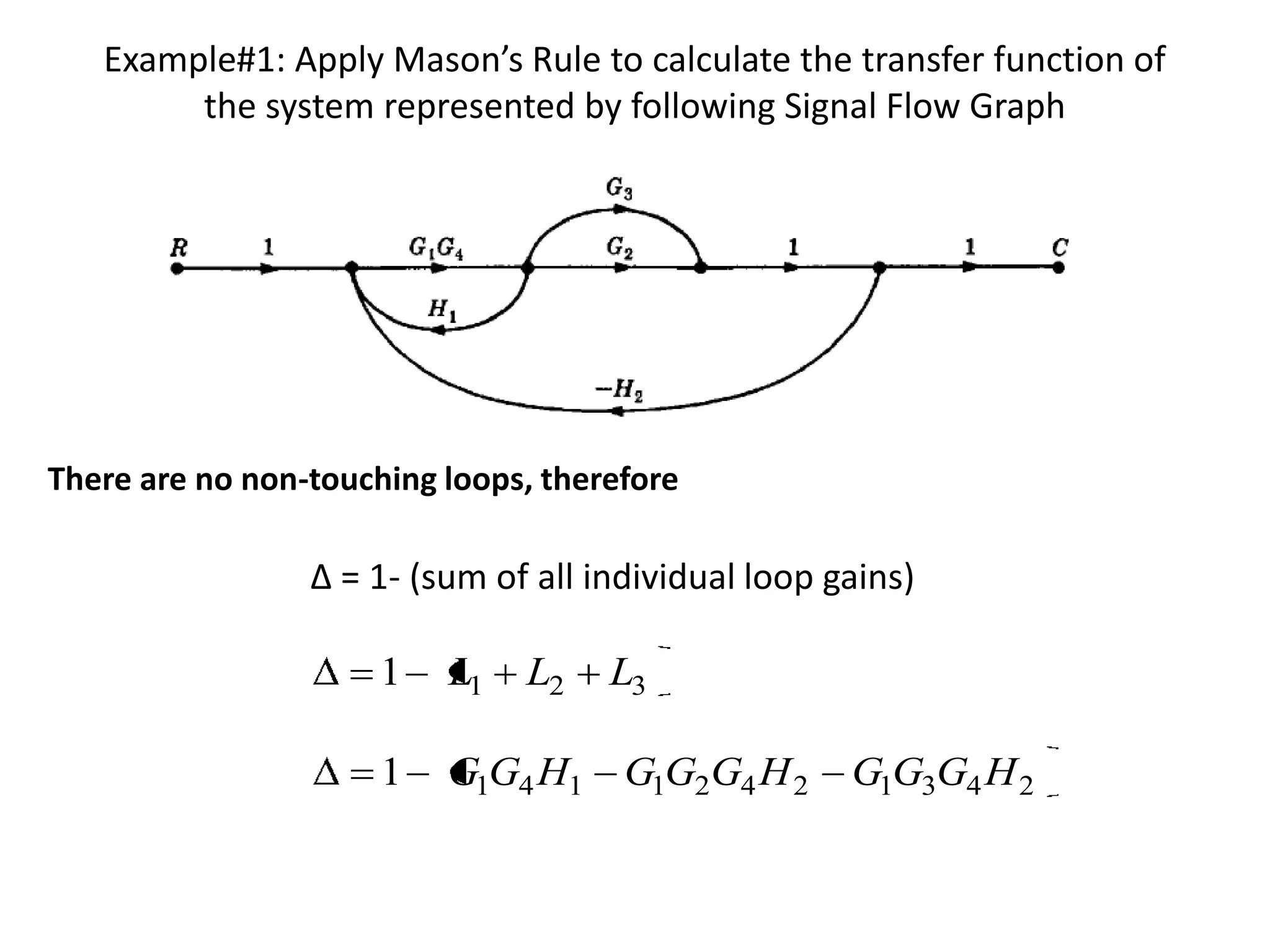
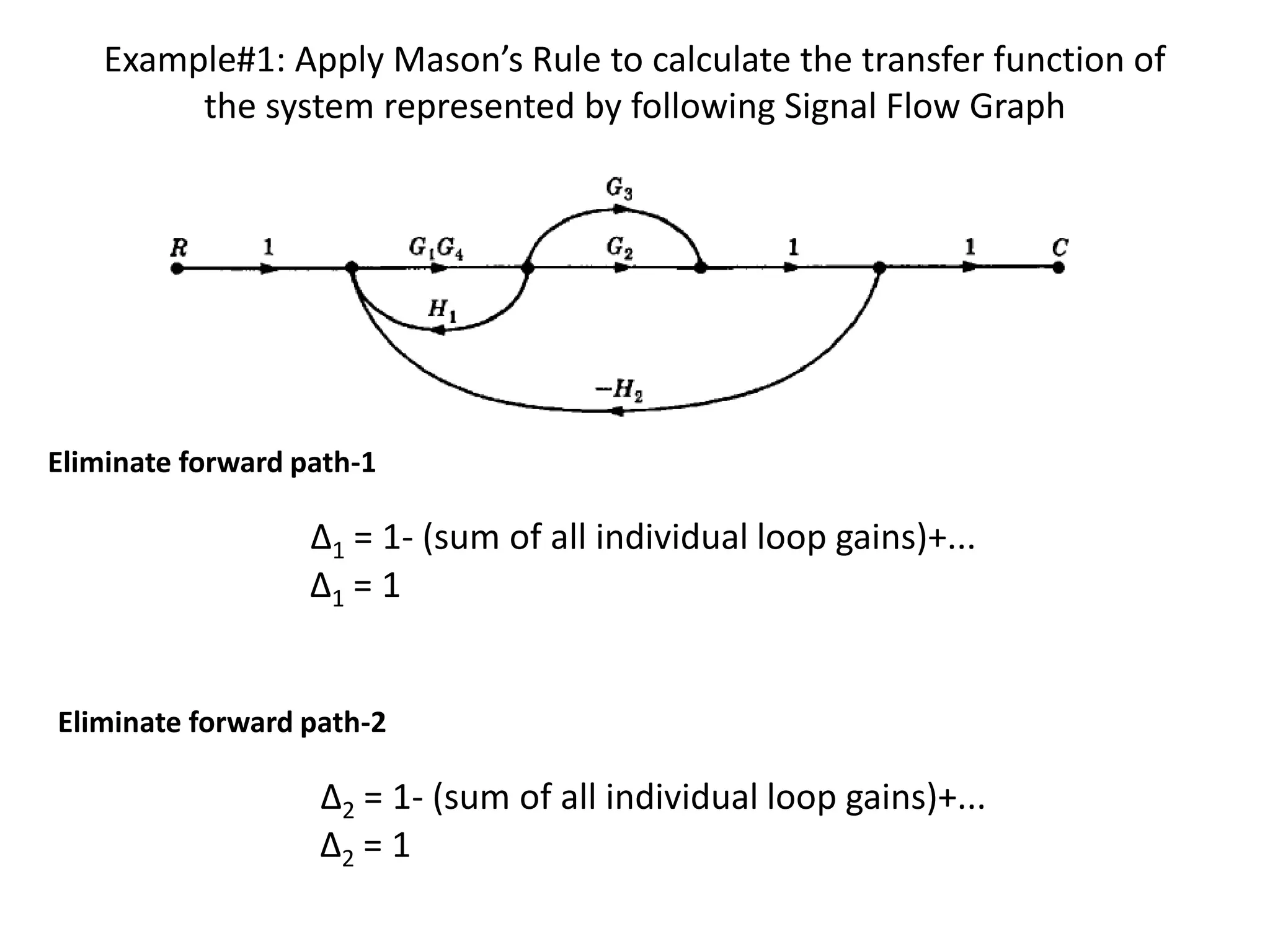
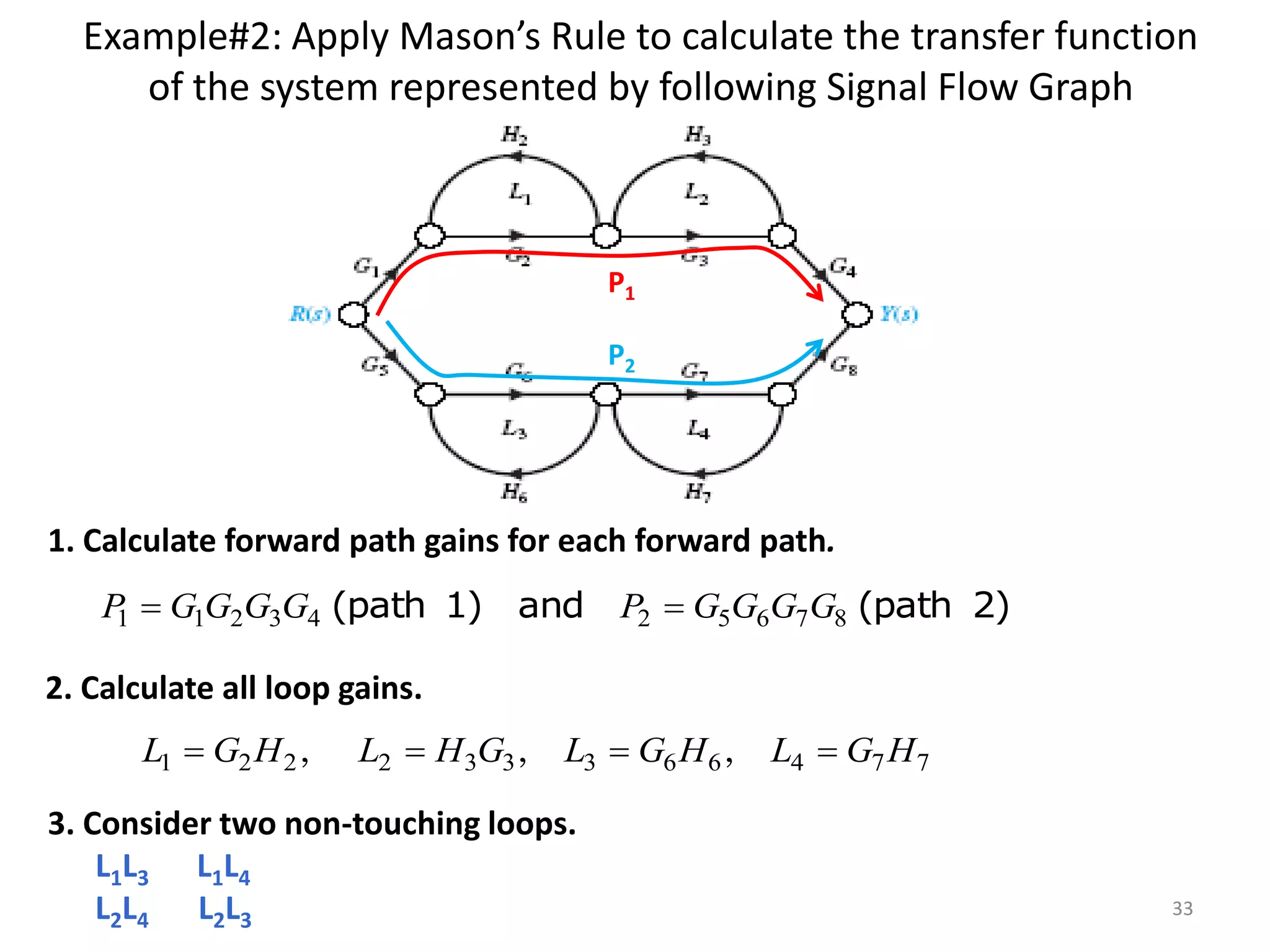
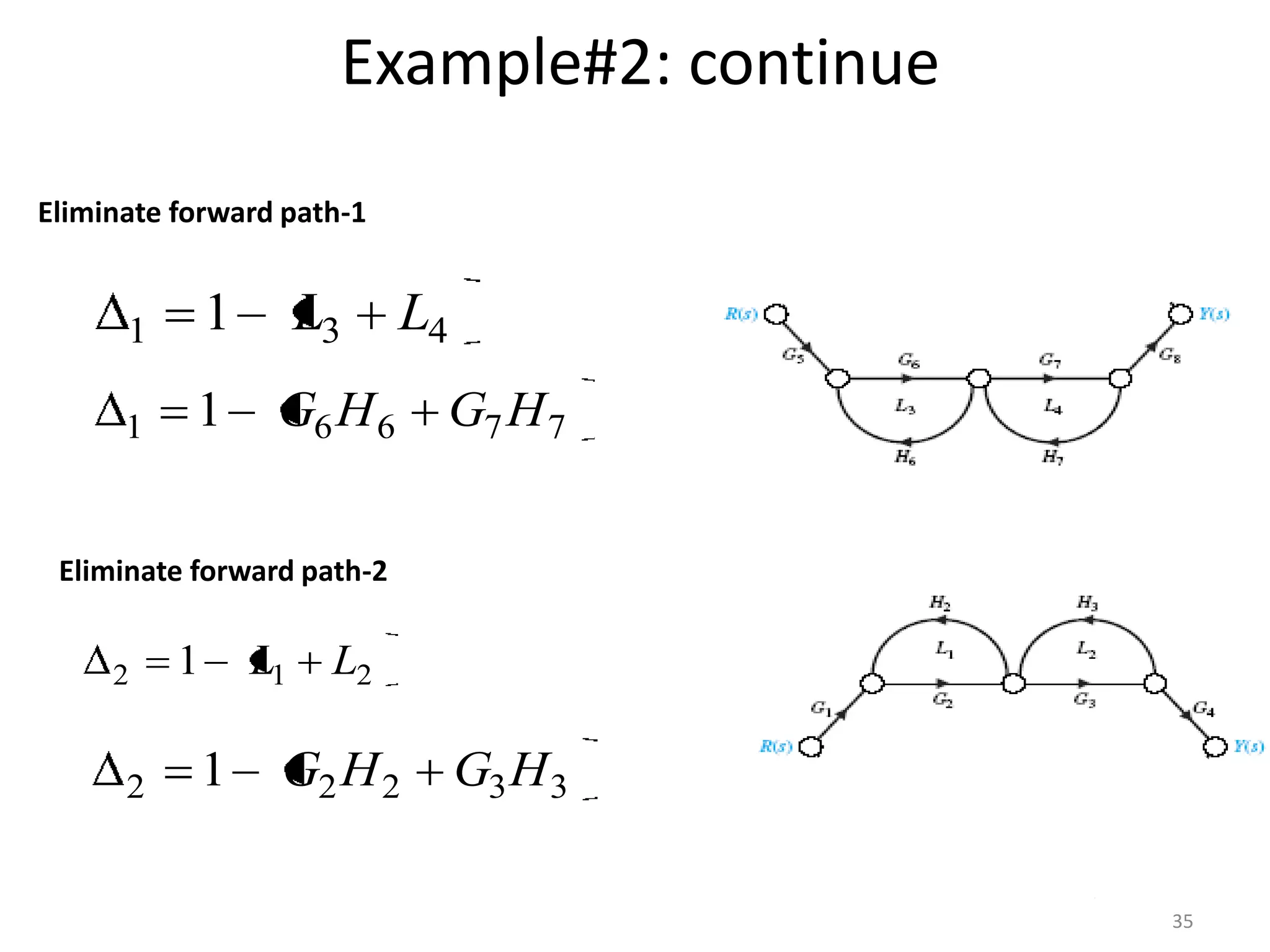
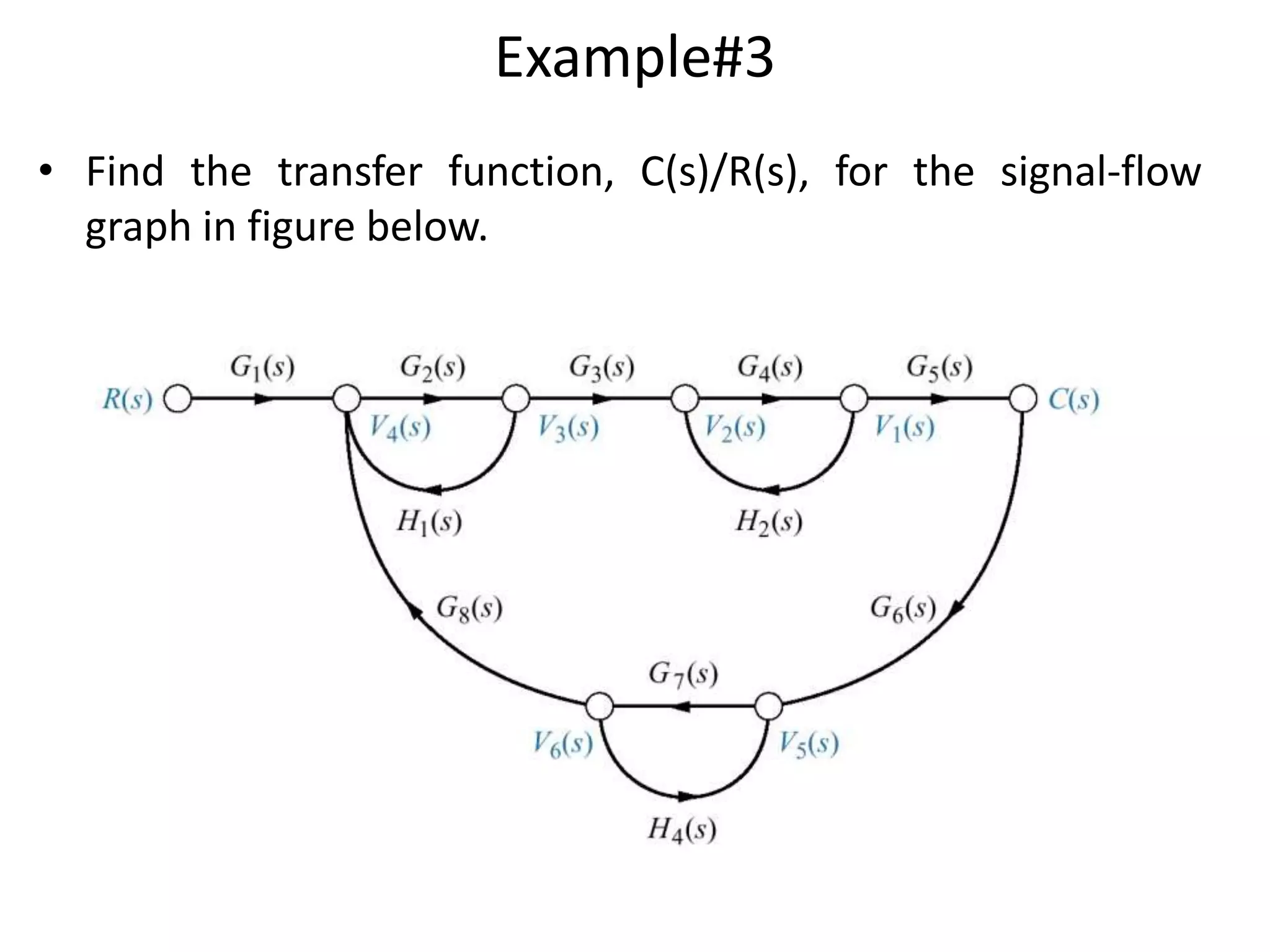
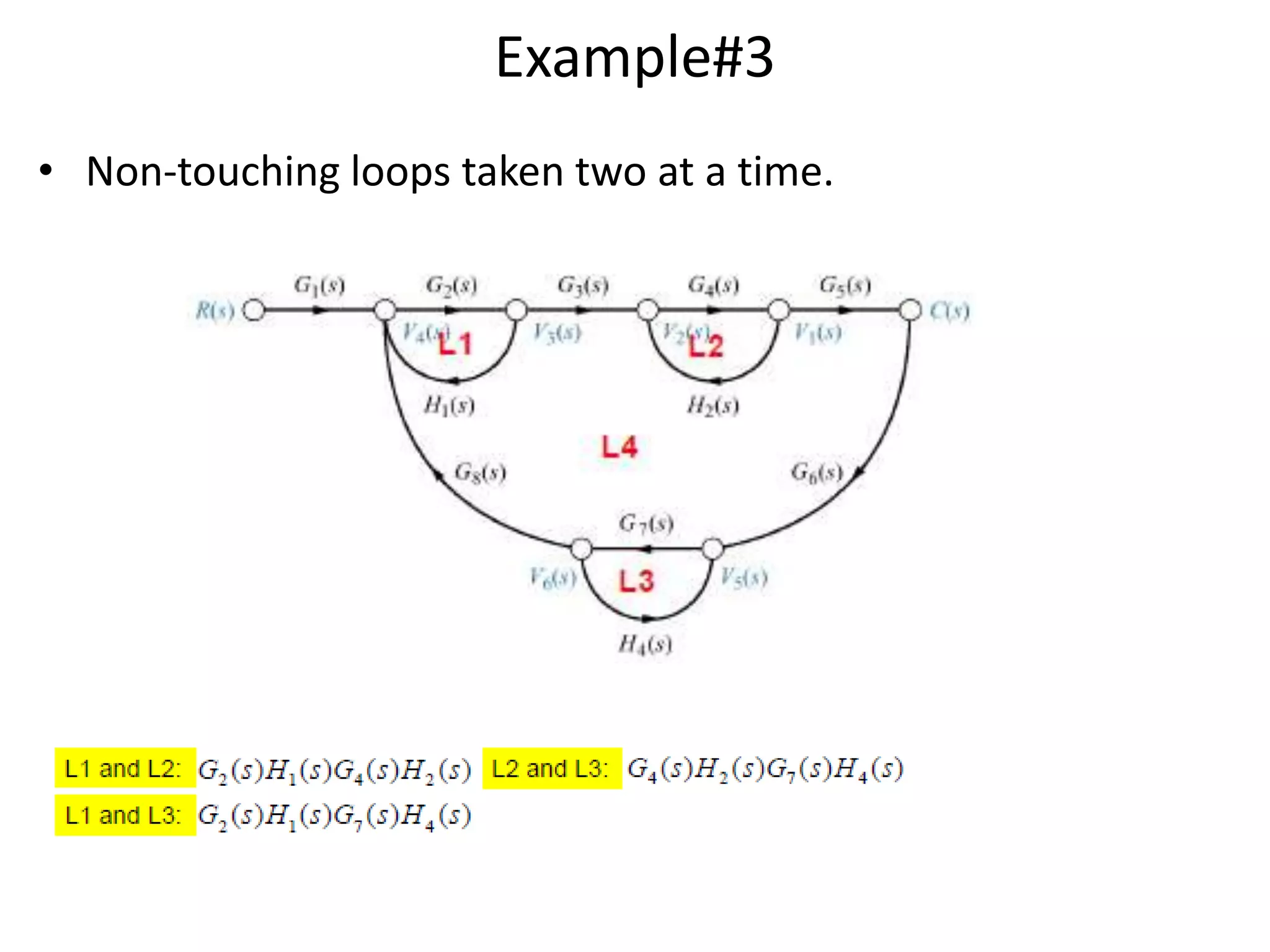
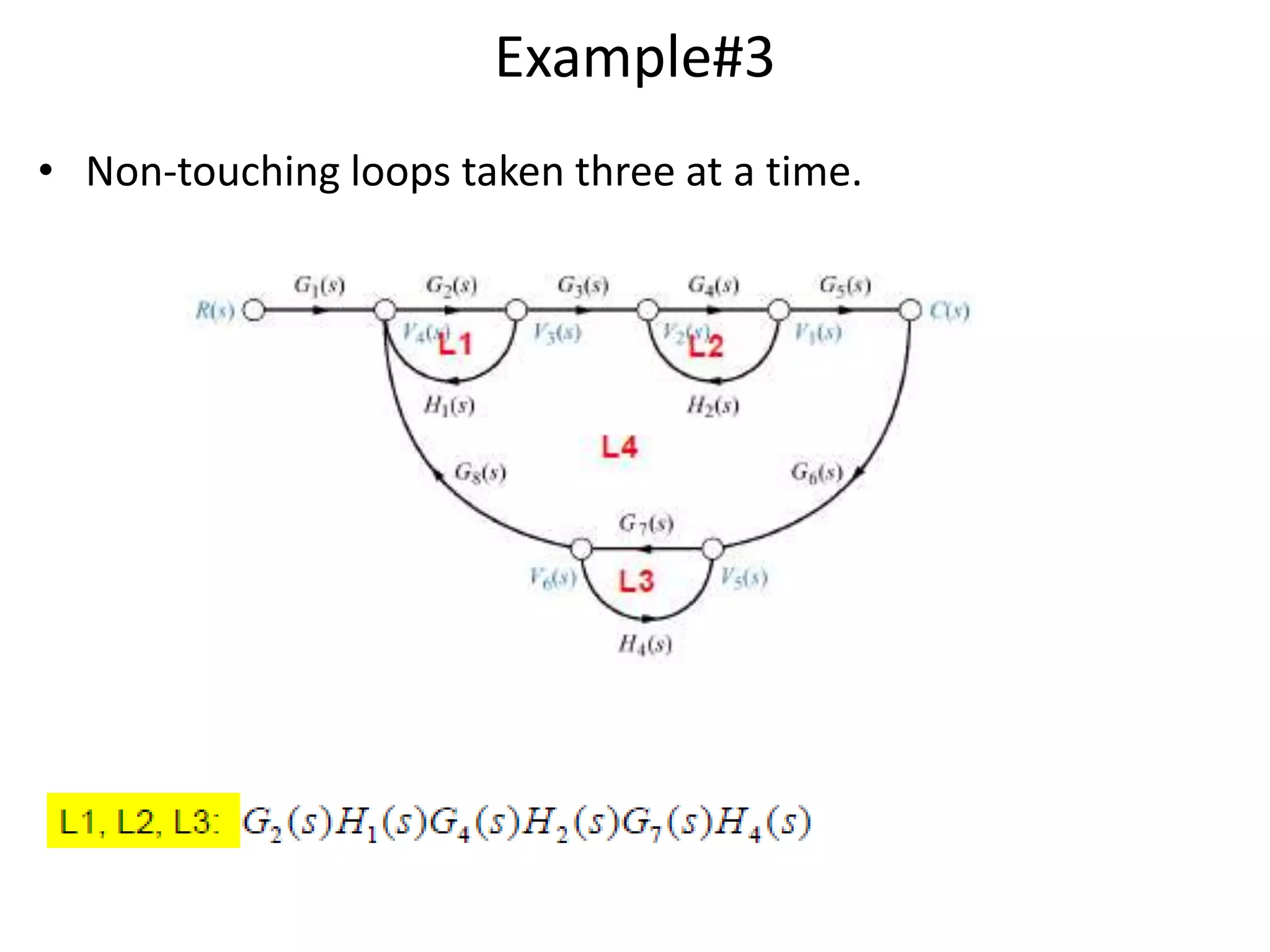
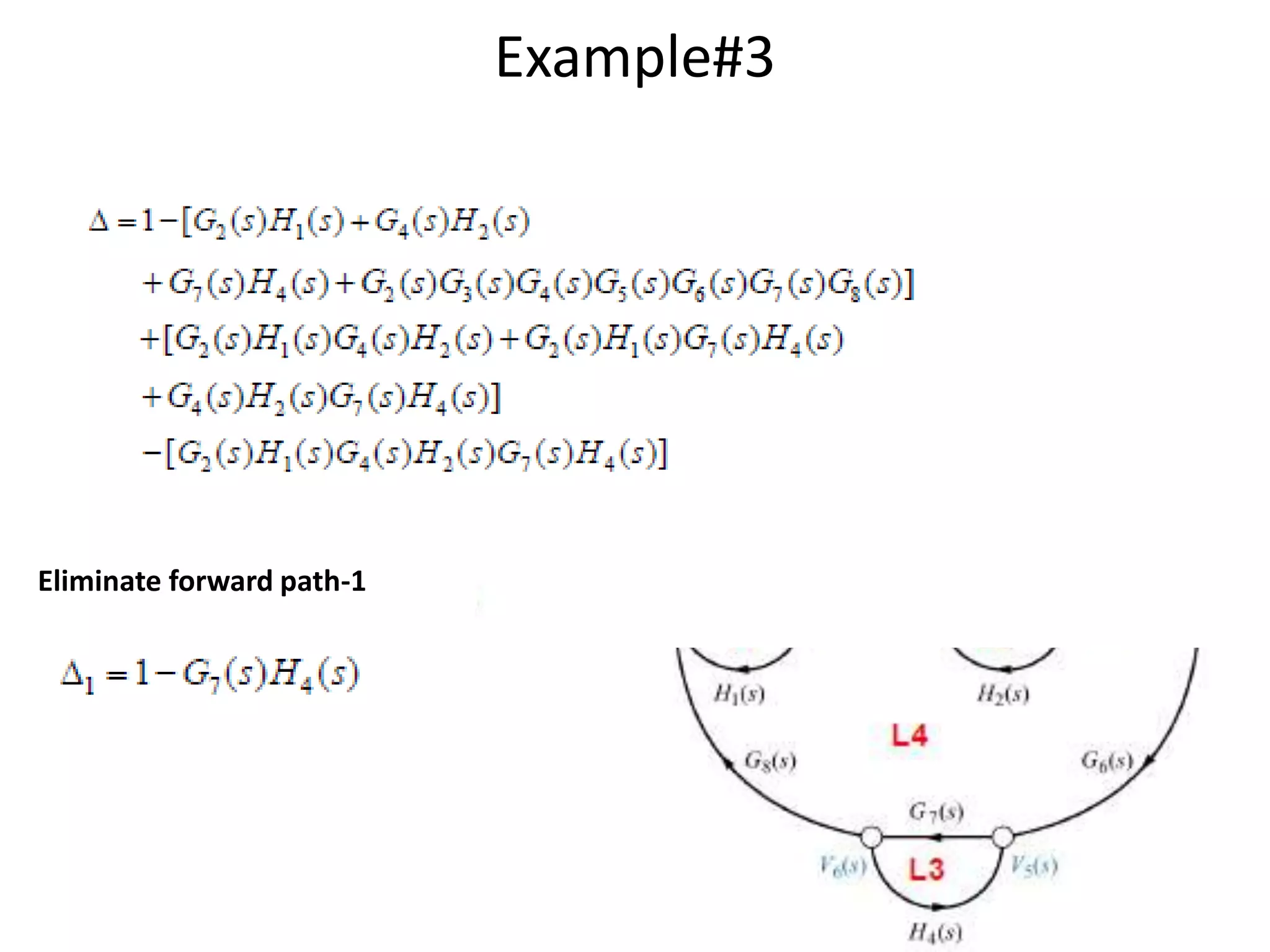
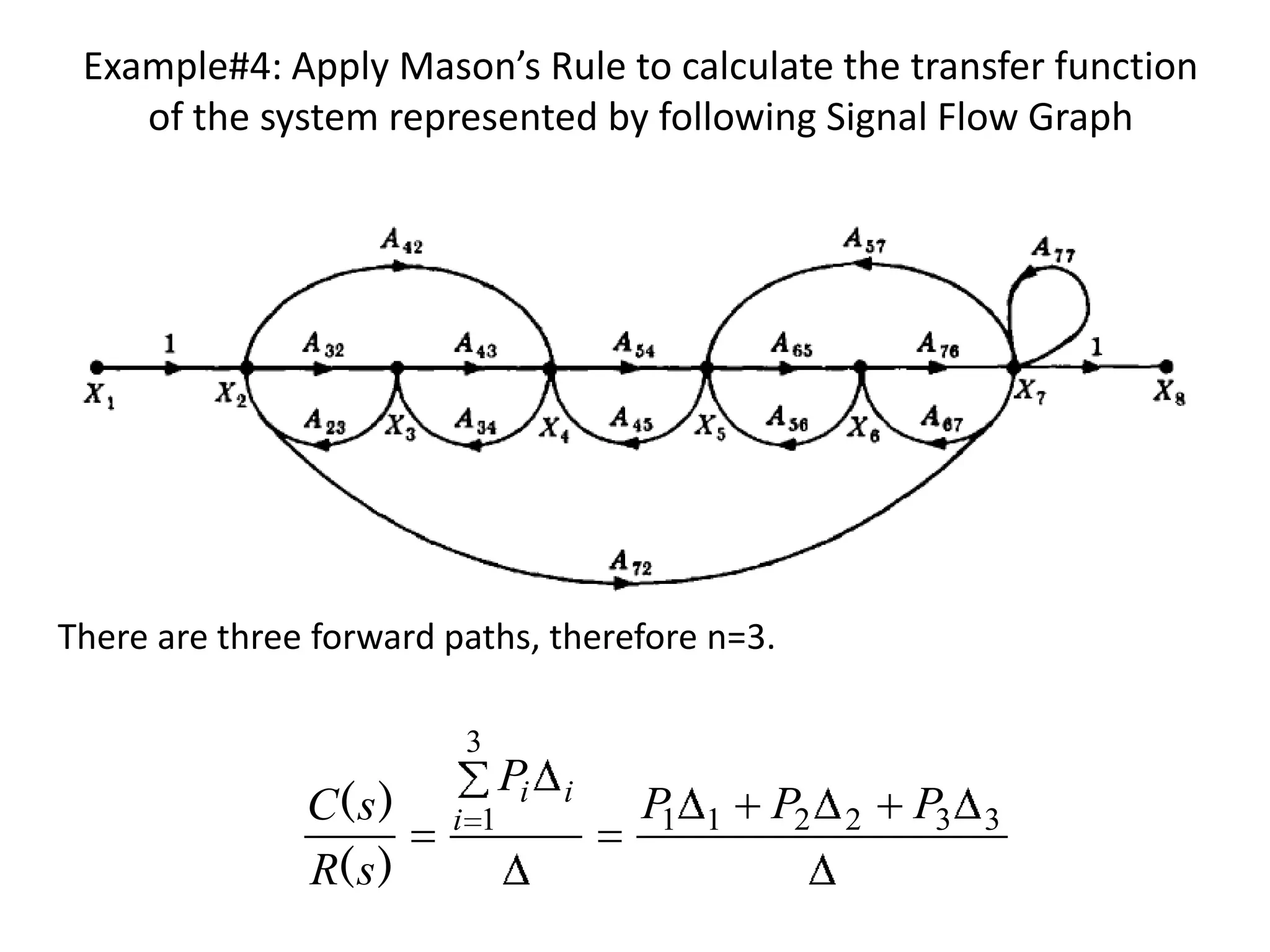
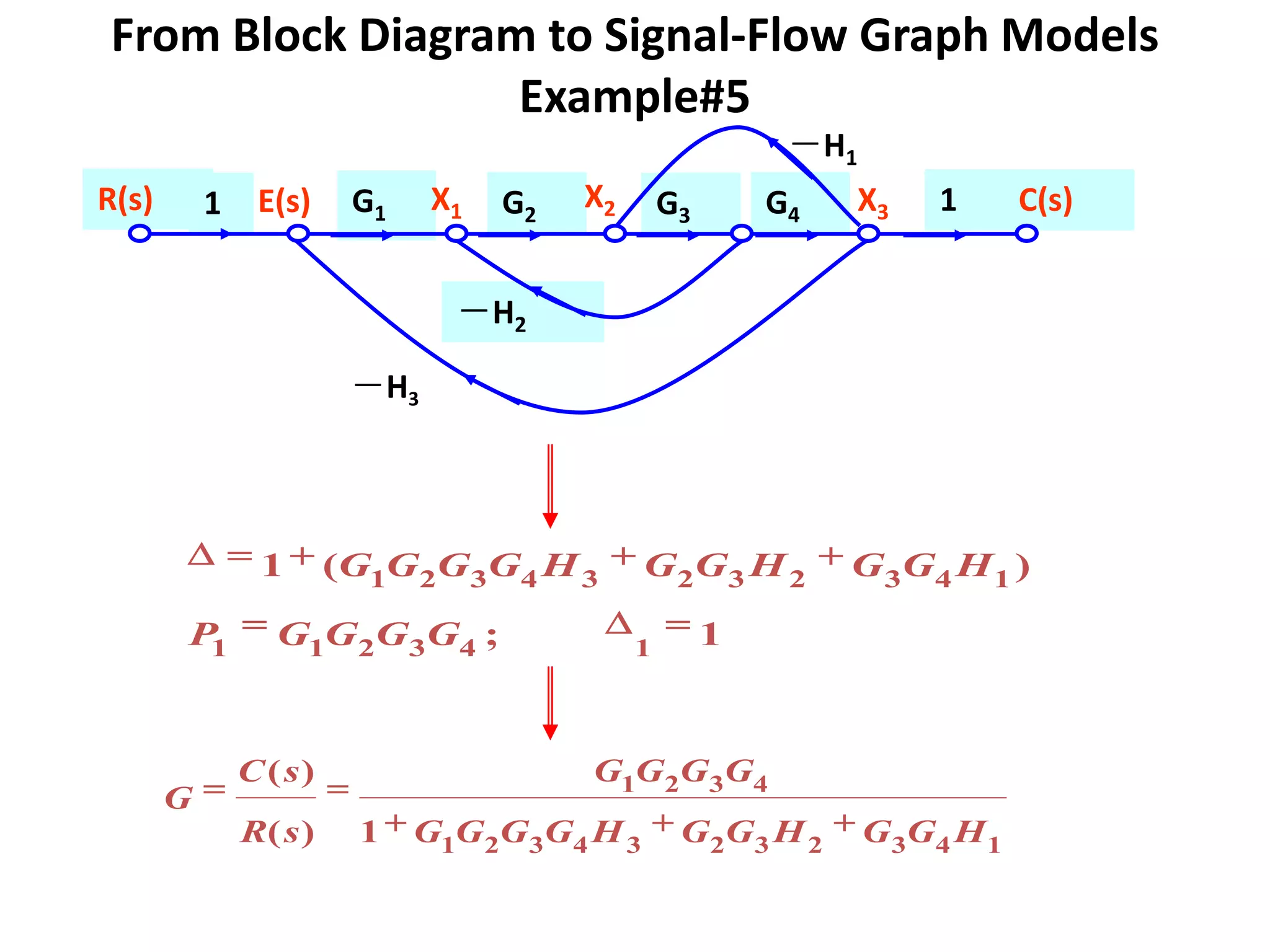
- Mason's gain formula for calculating the transfer function of a system from its signal flow graph representation in 3 sentences or less
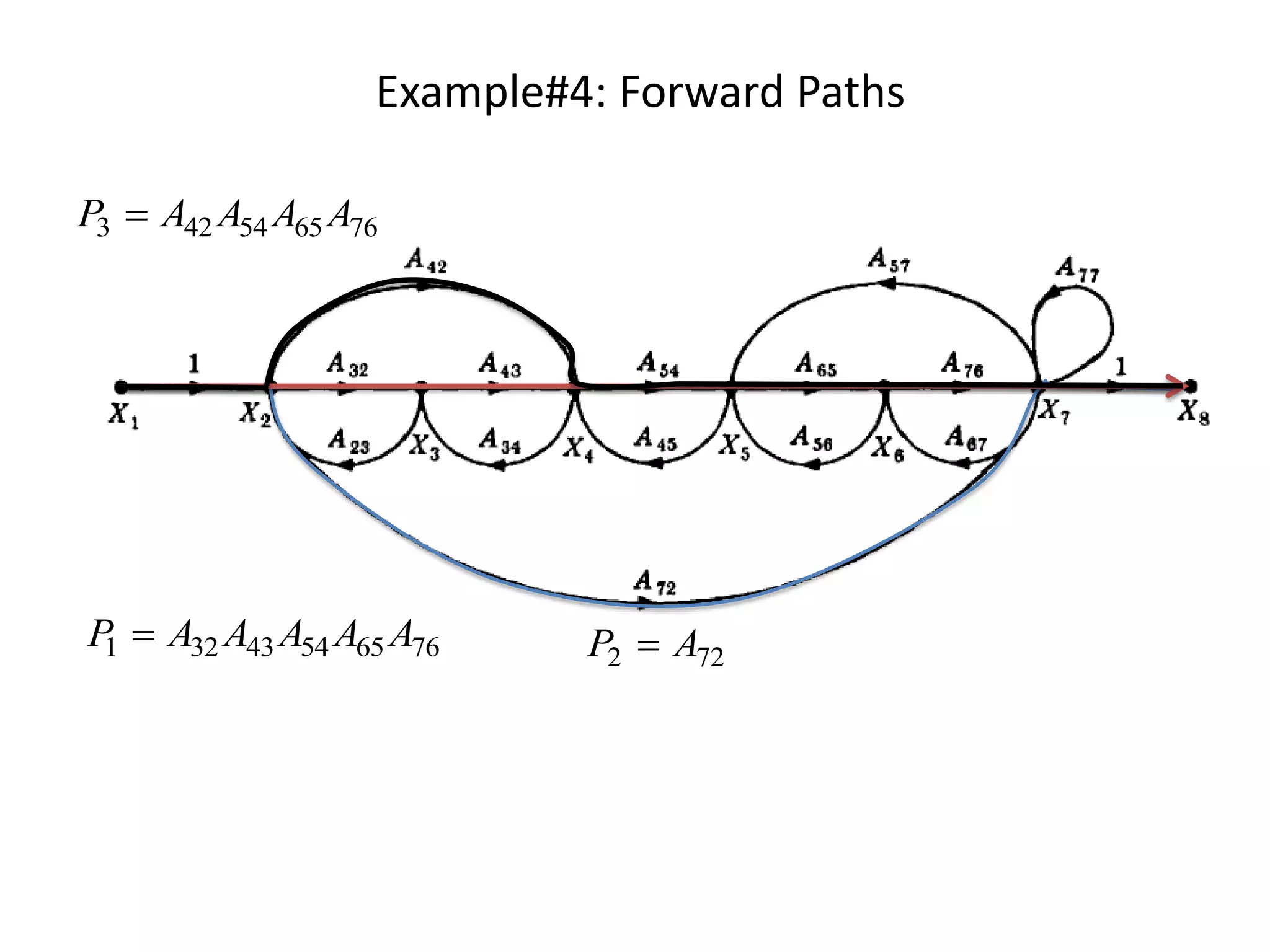
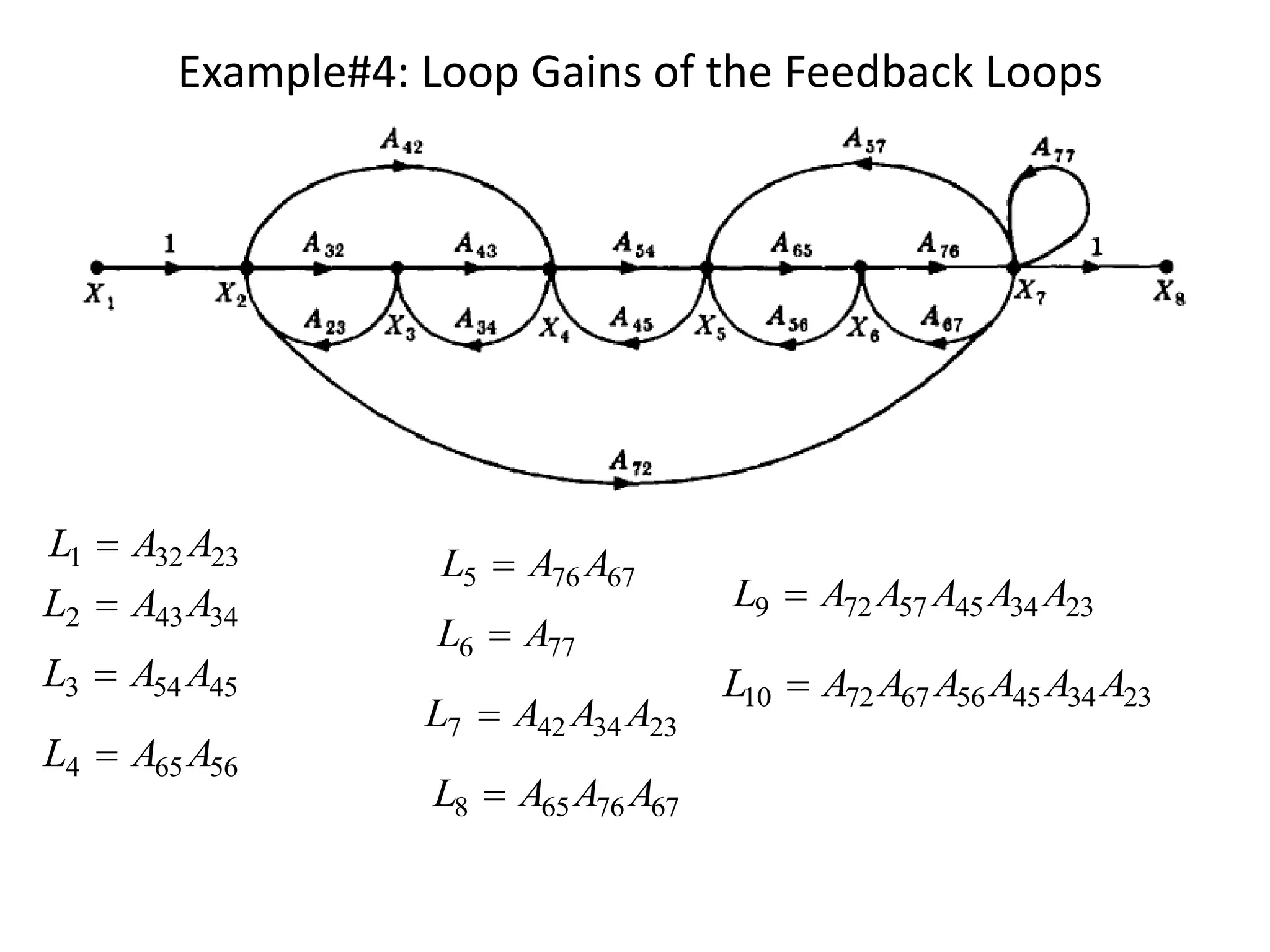
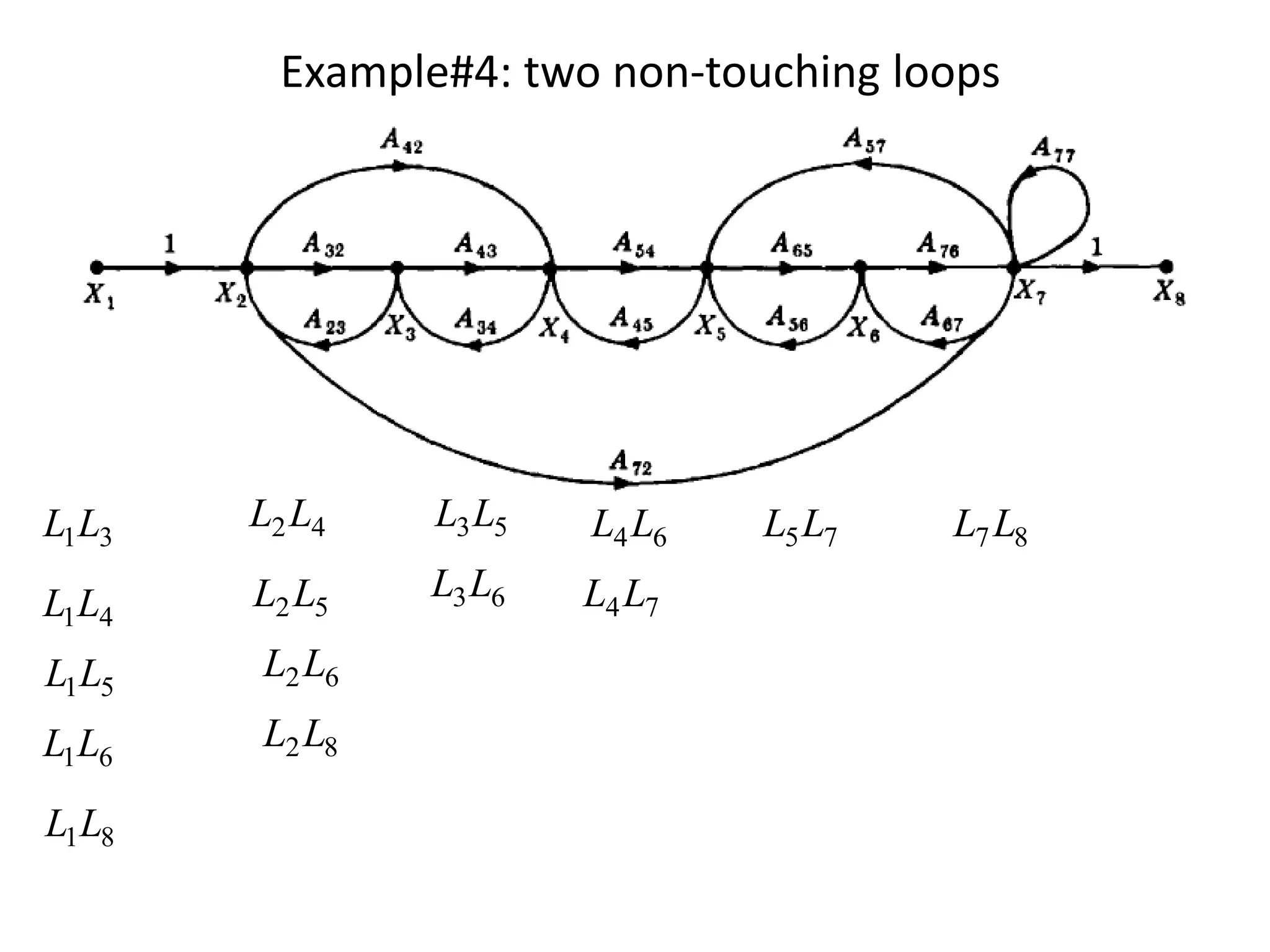
- Examples are provided to demonstrate applying Mason's gain formula to calculate transfer functions from given signal flow graphs.