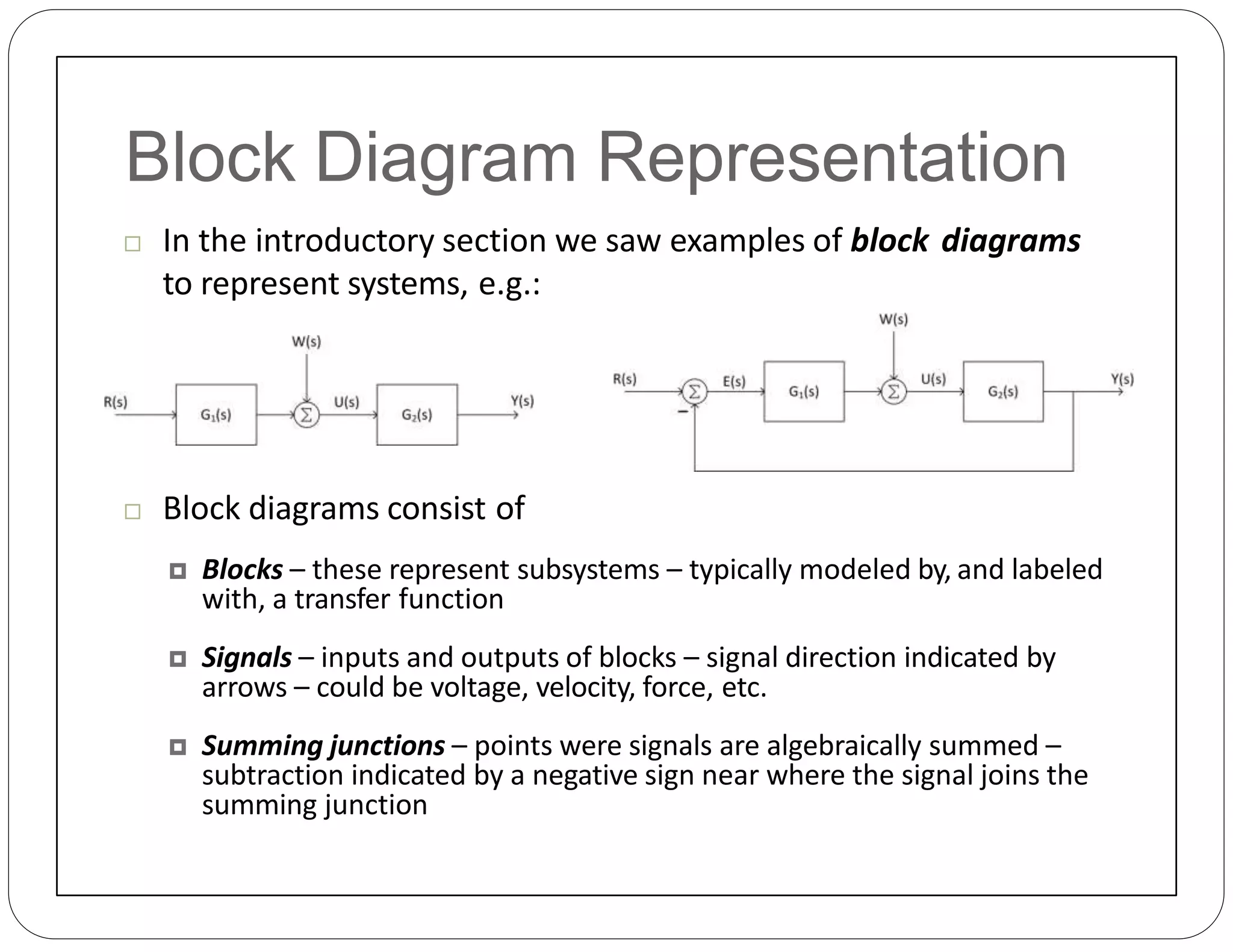
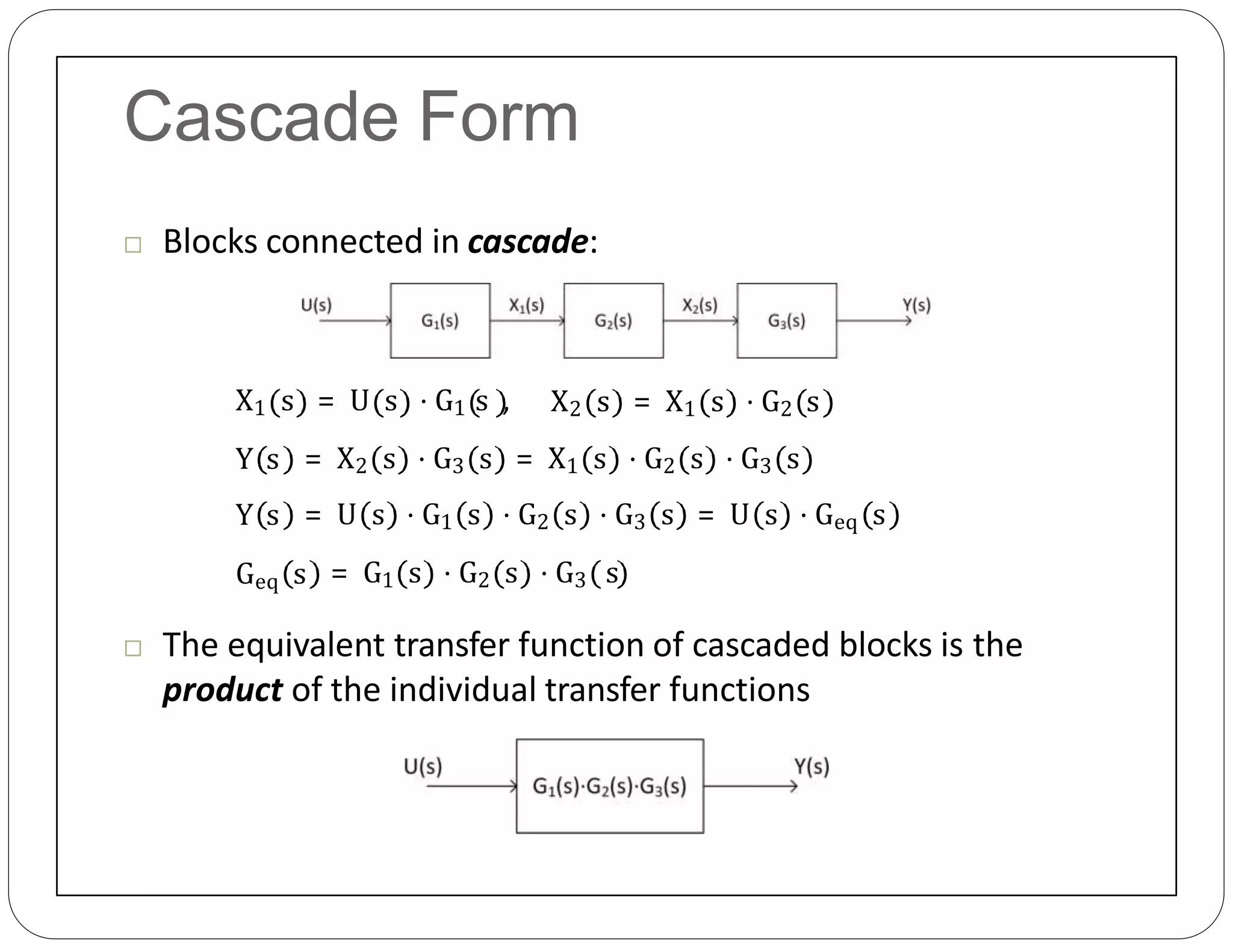
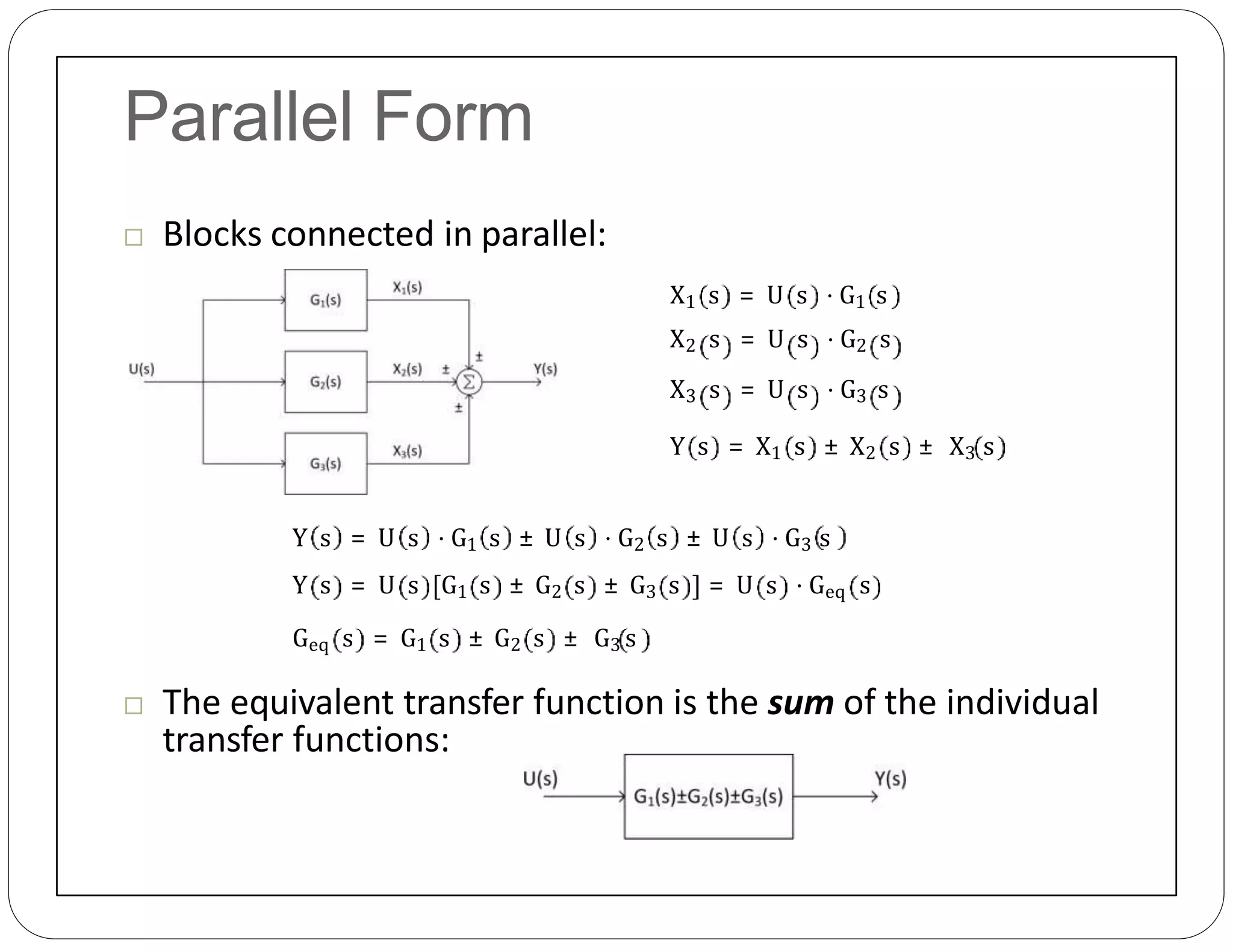
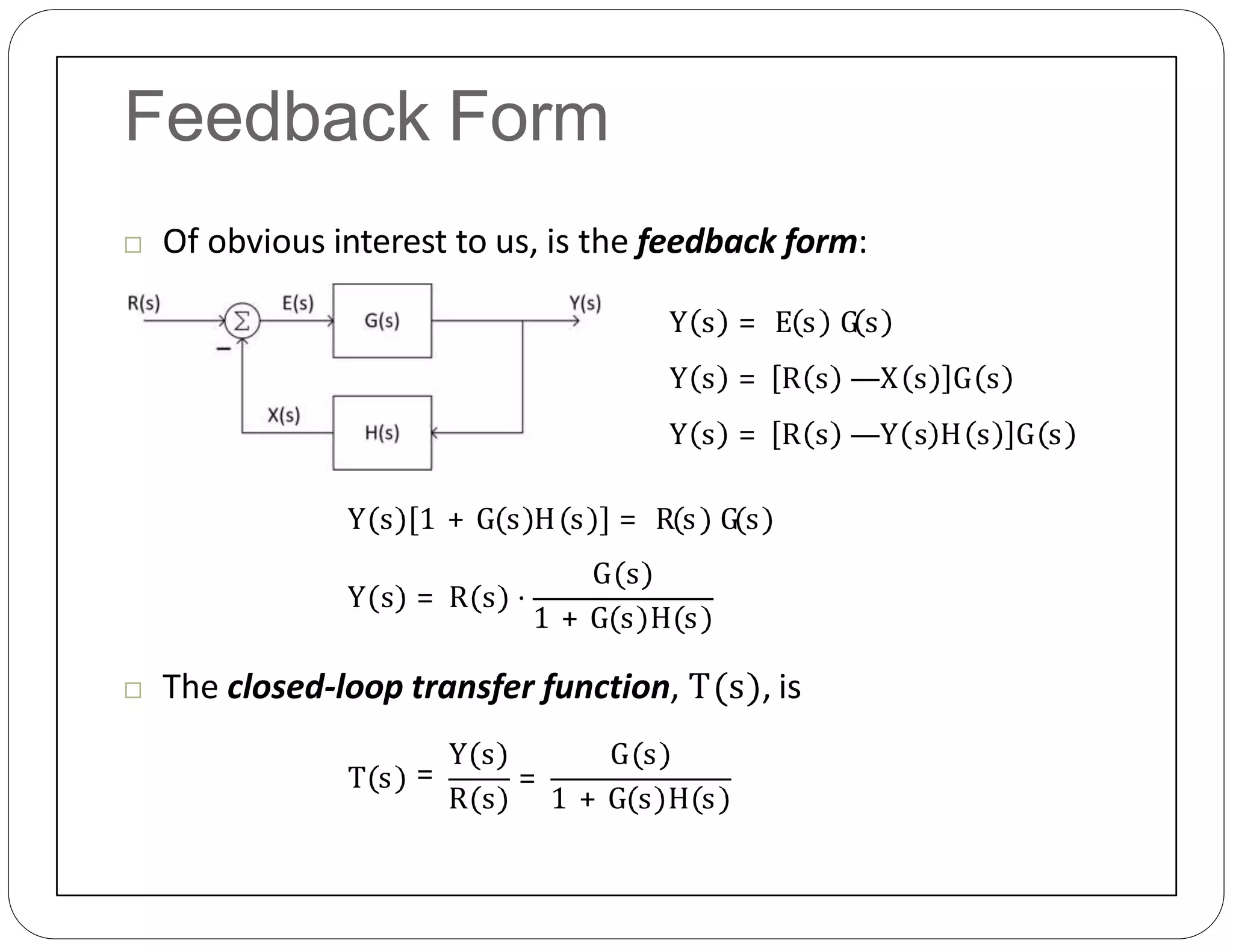
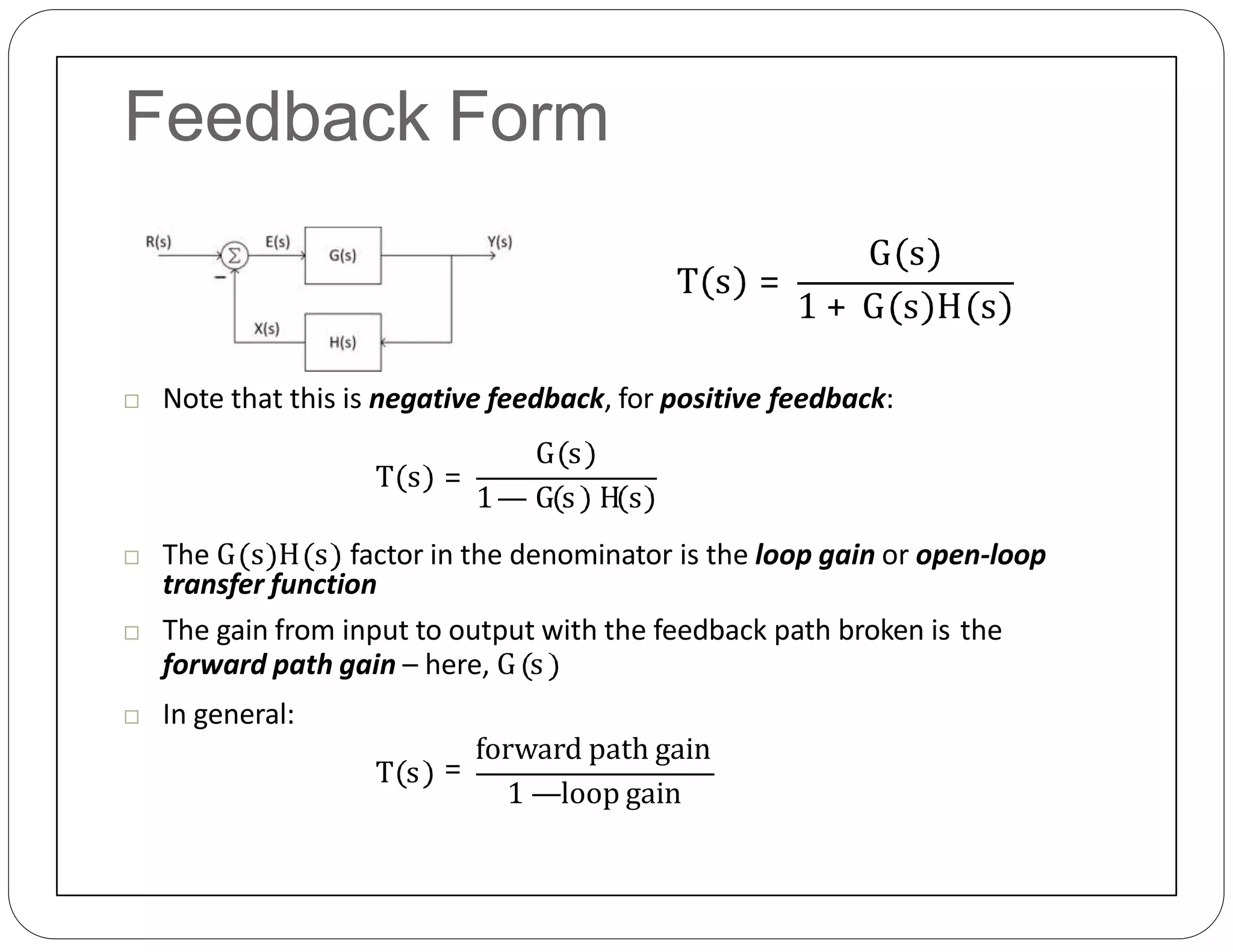
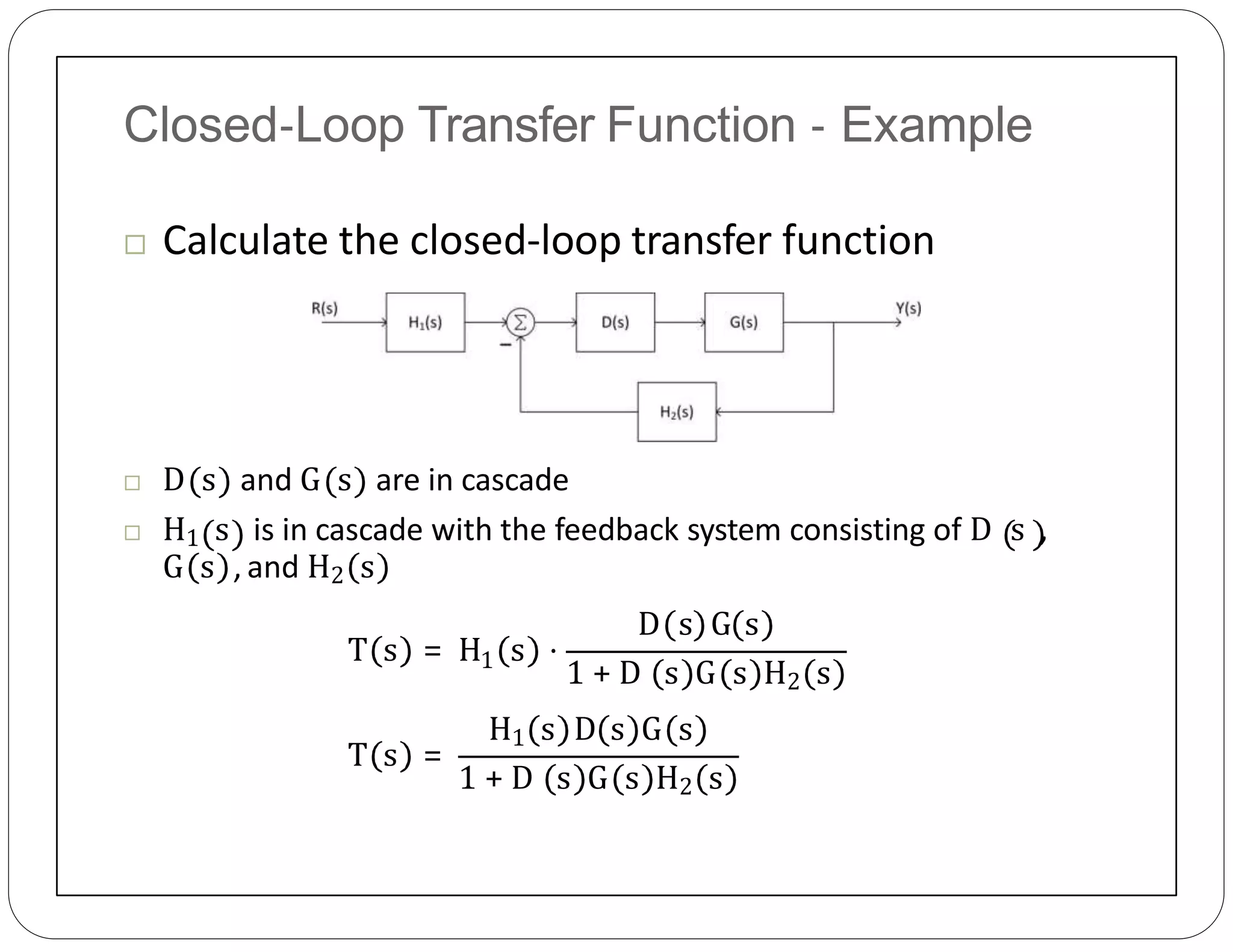
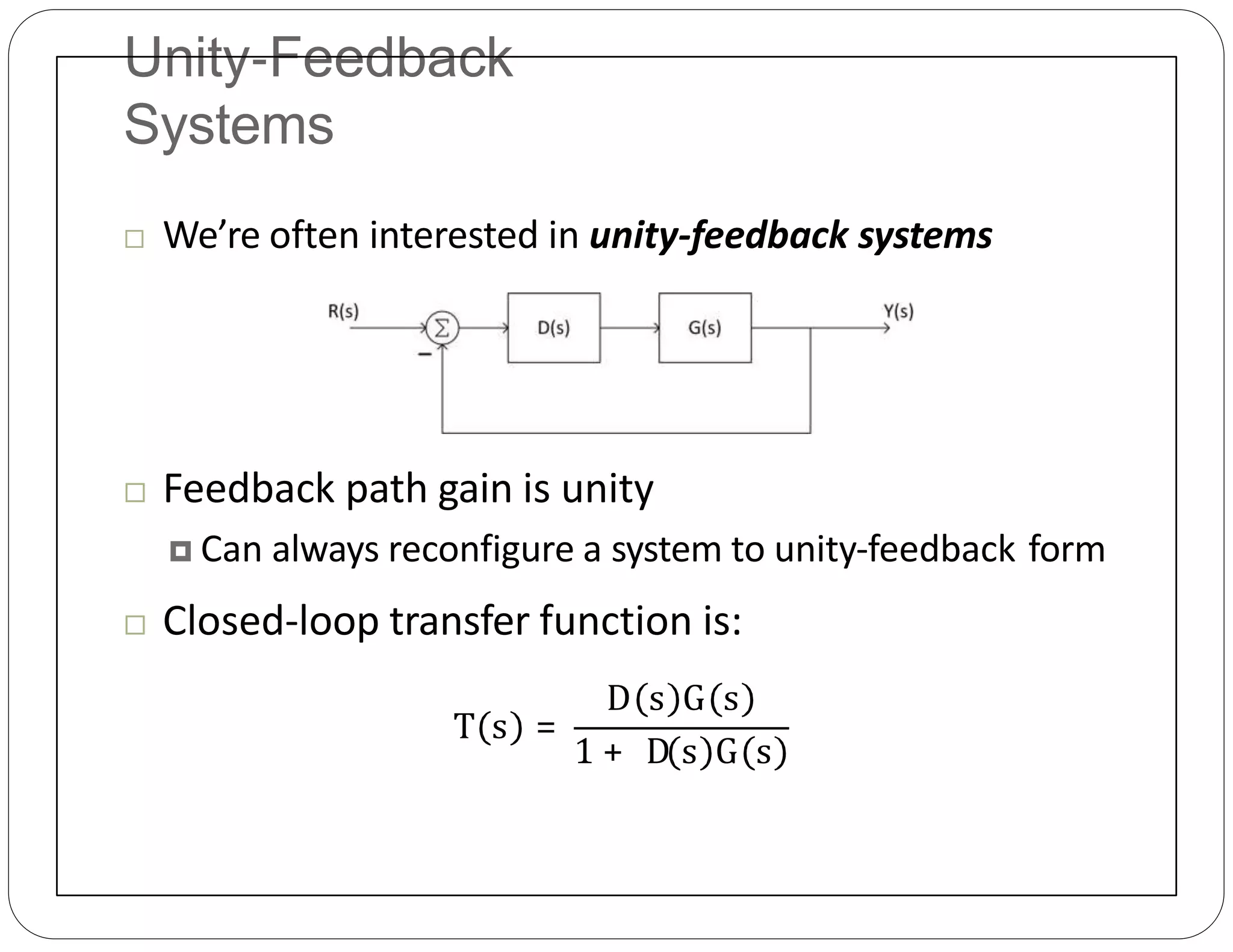
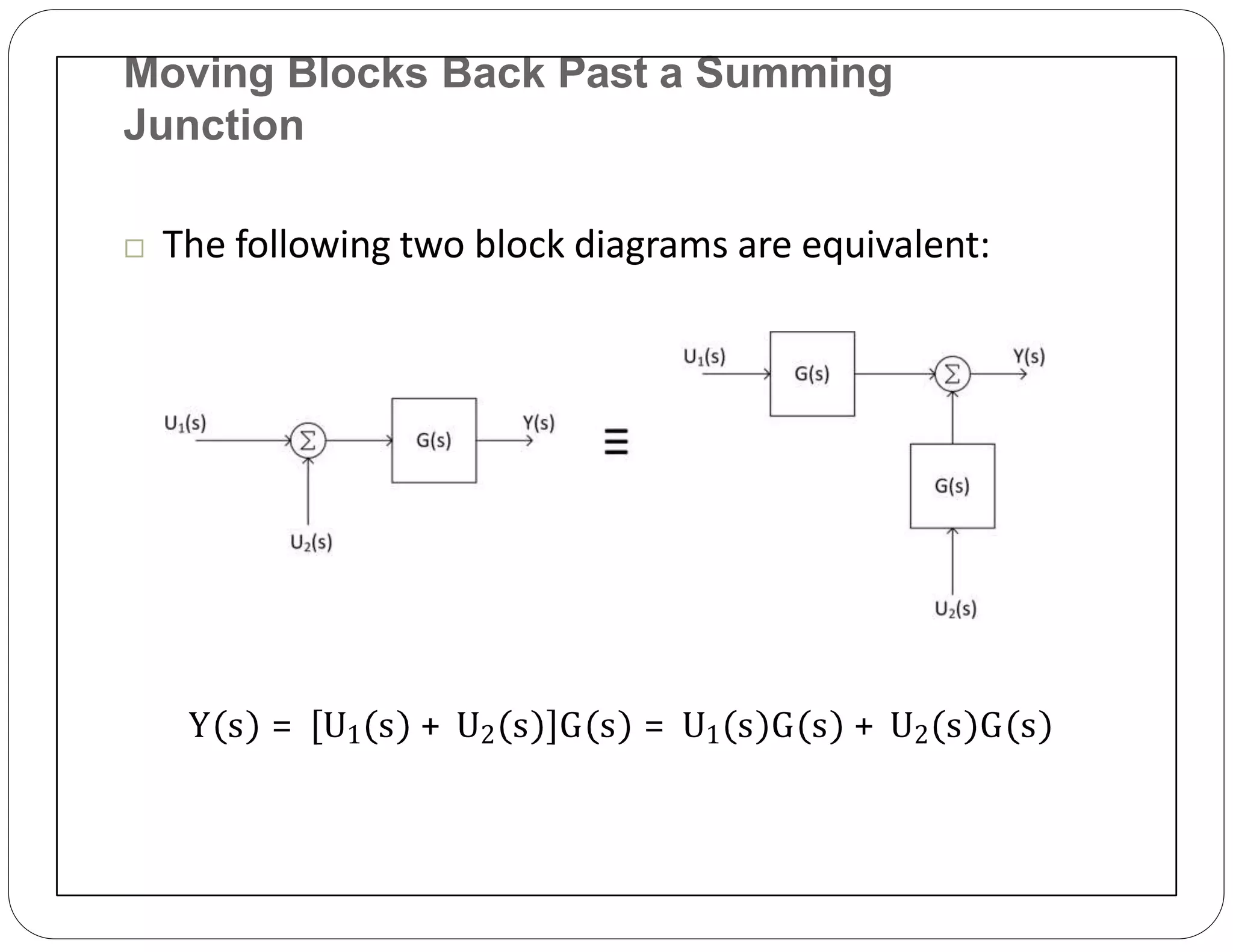
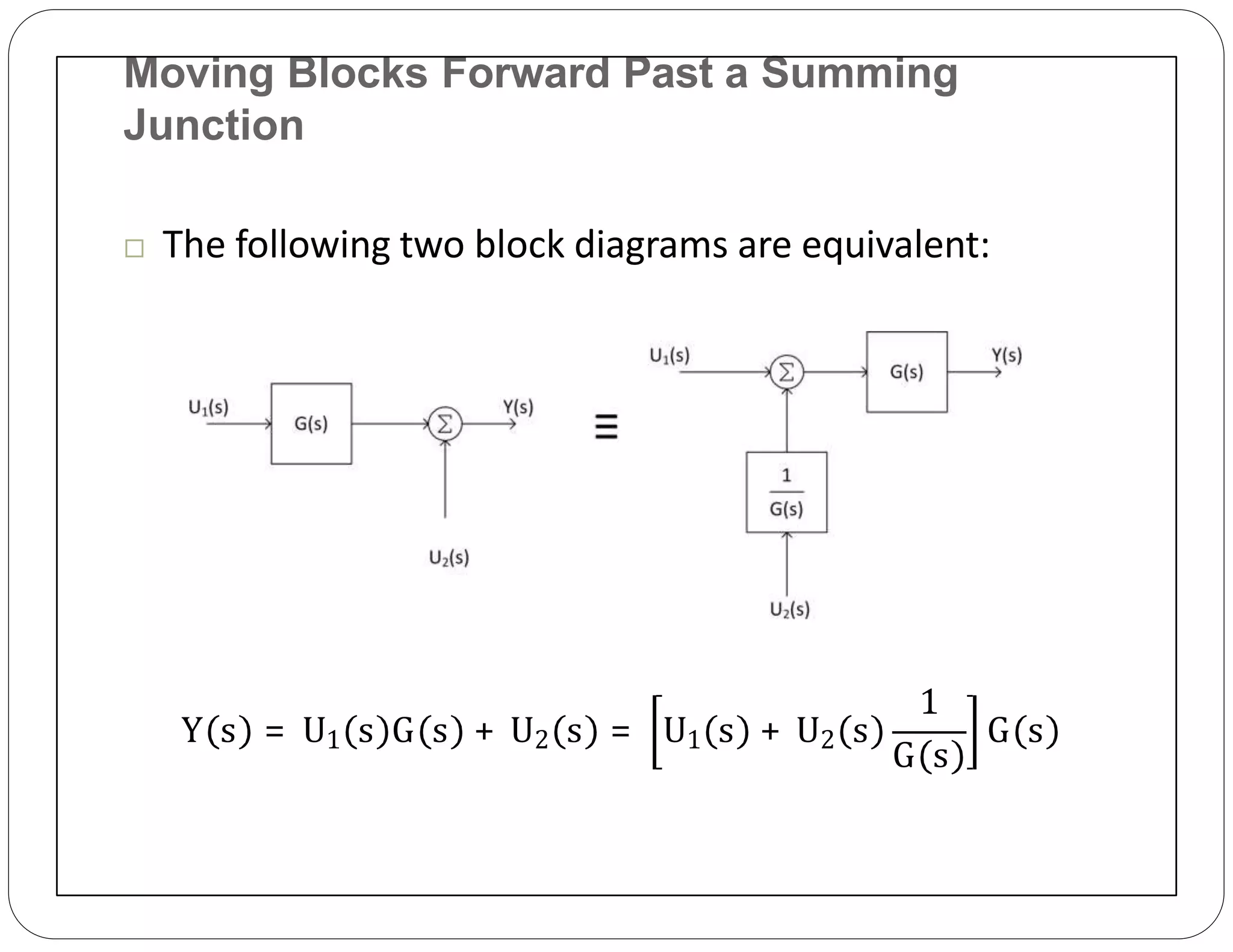
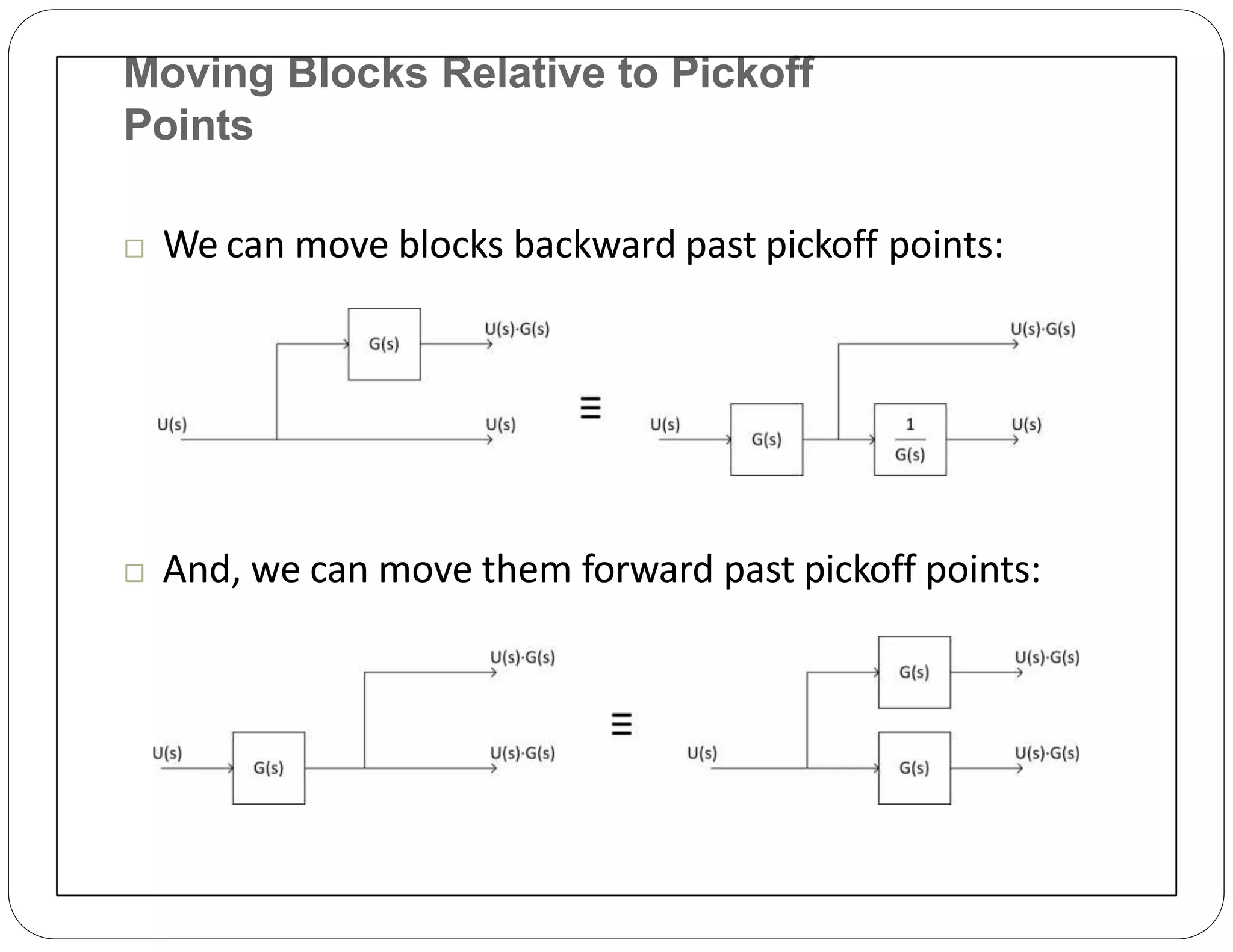
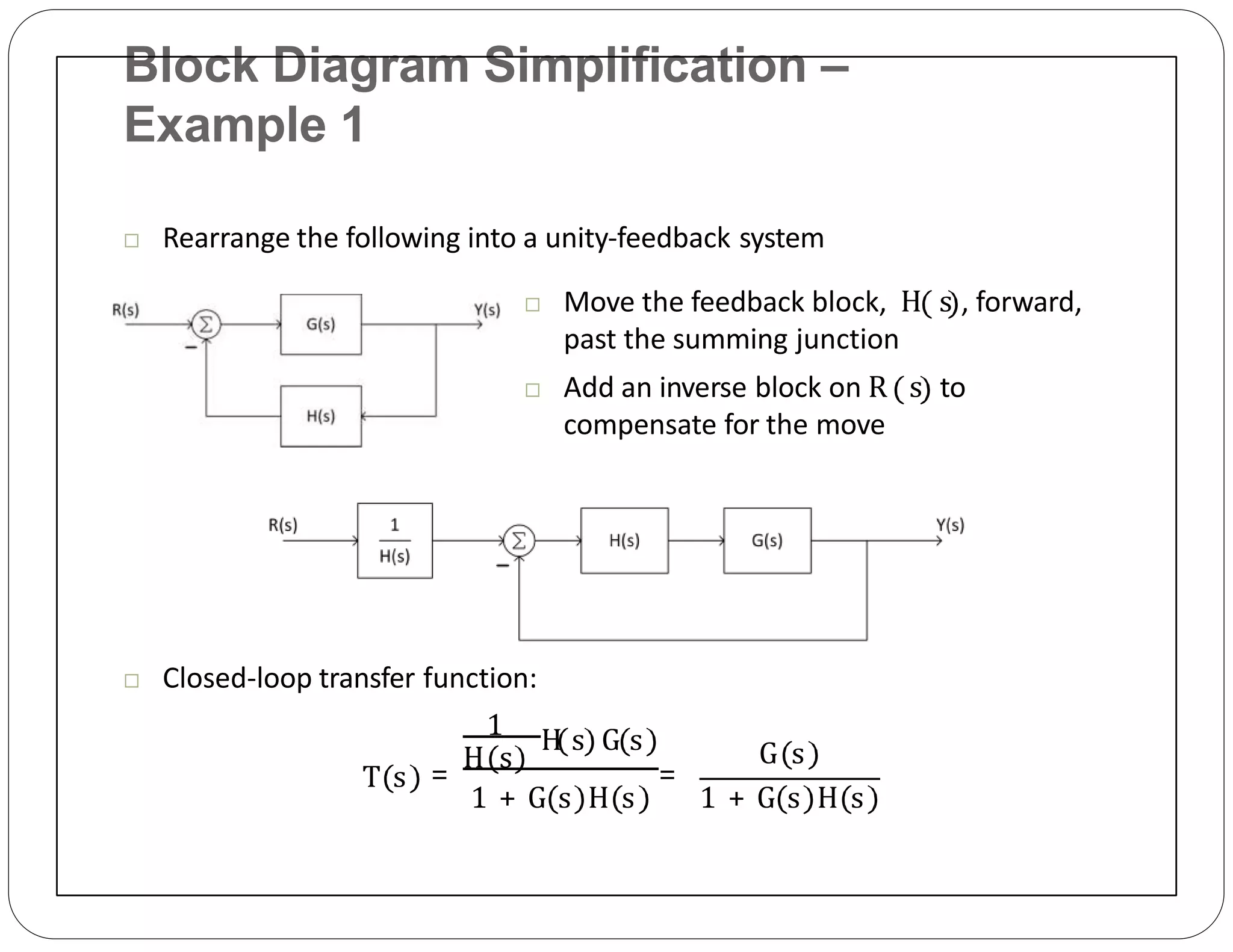
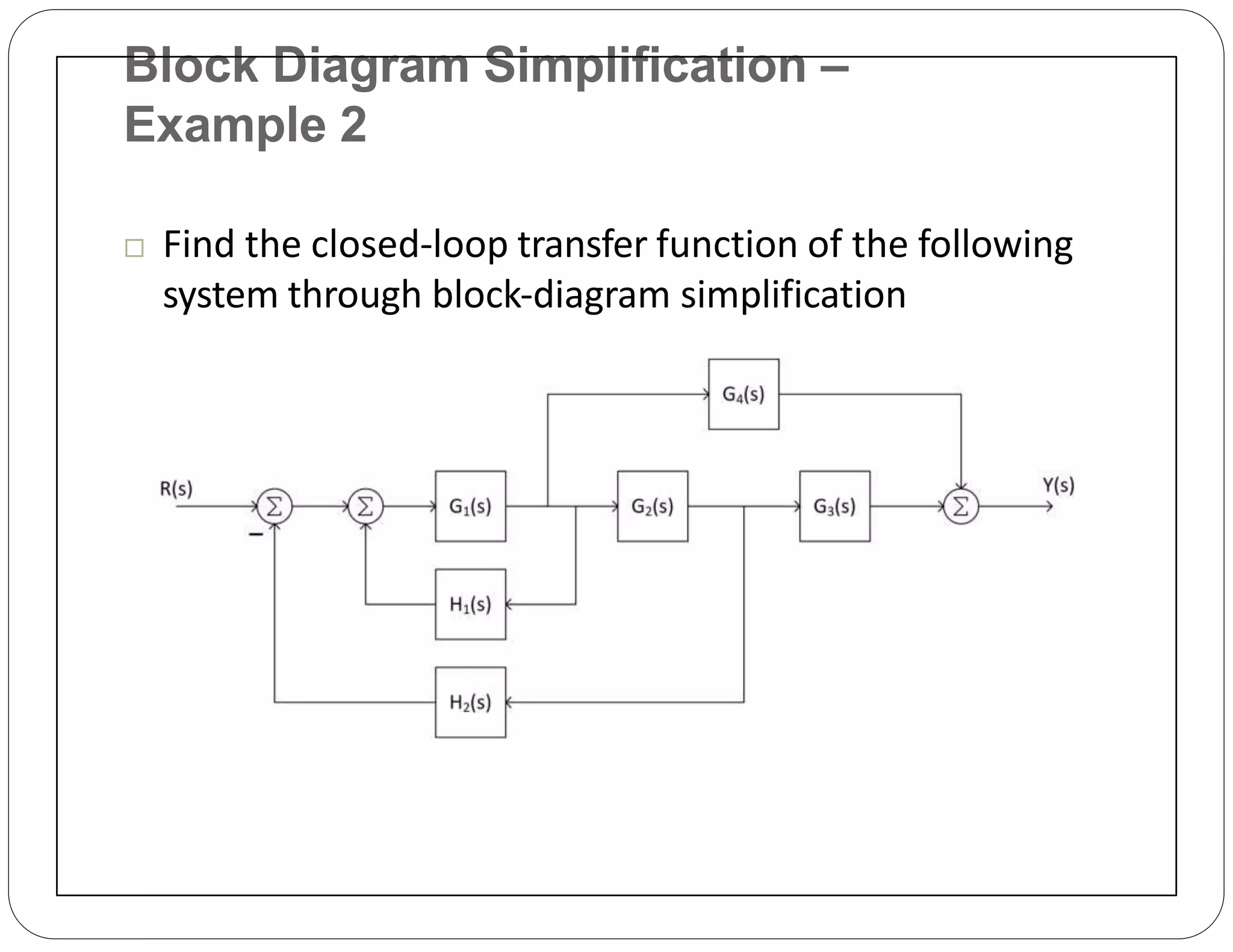
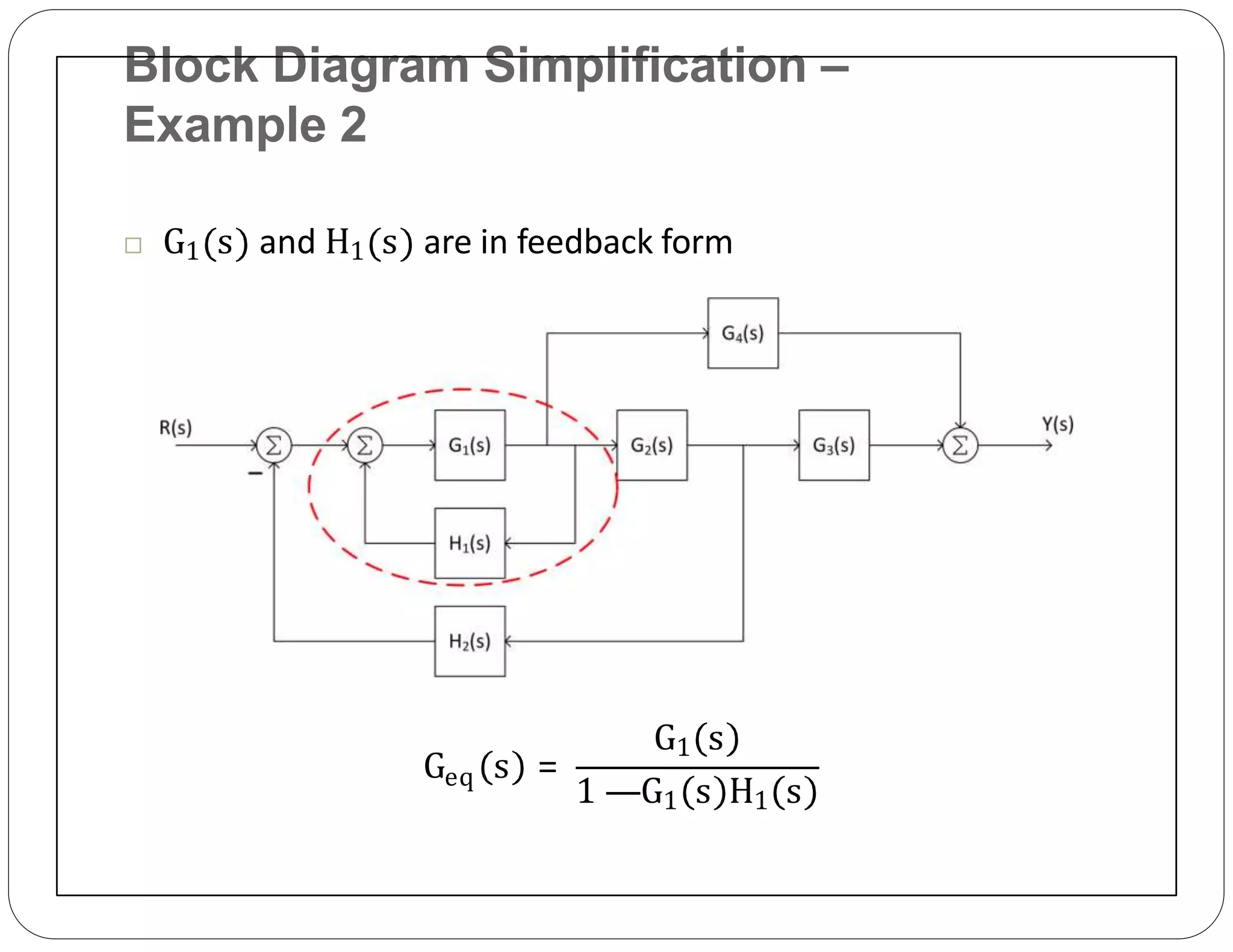
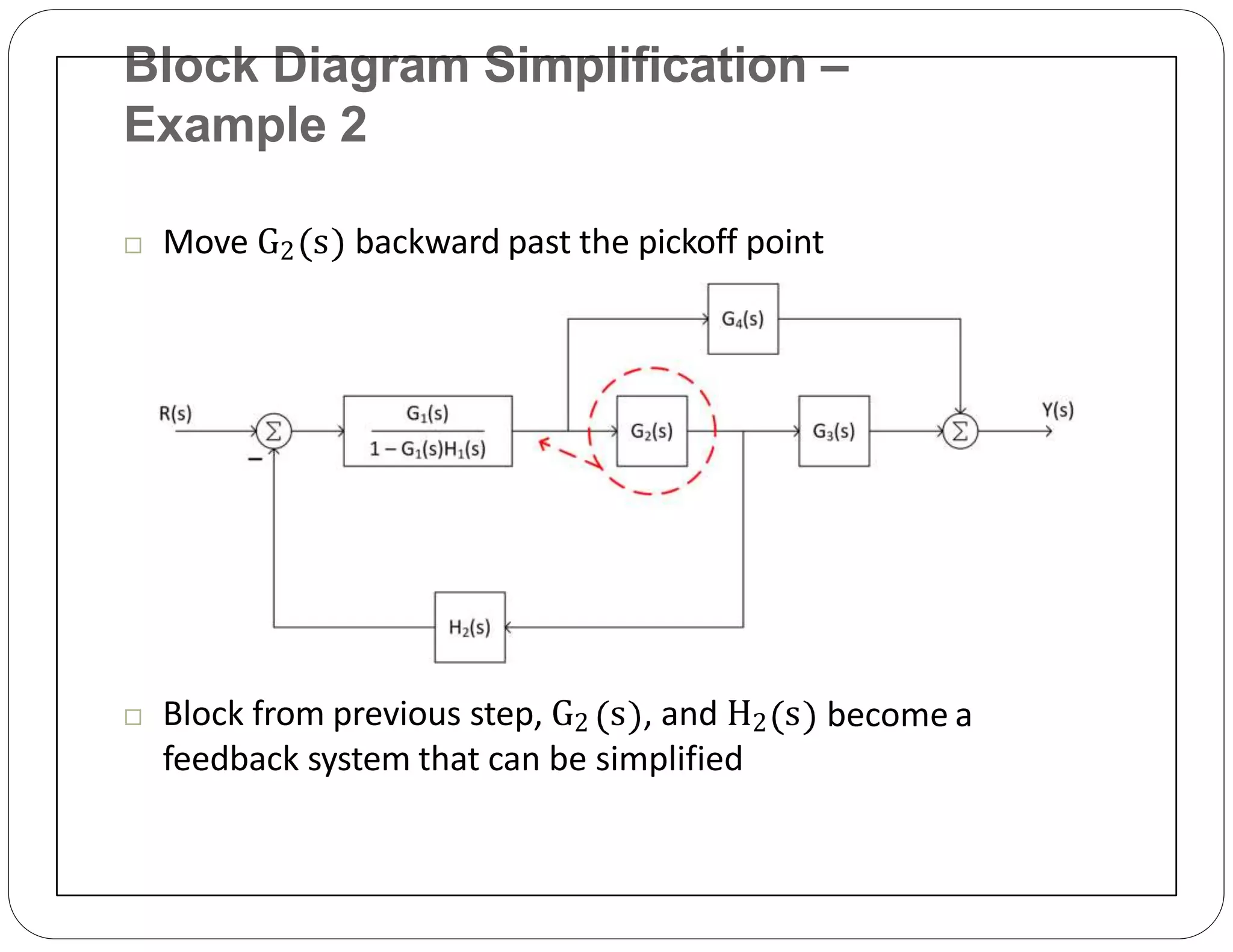
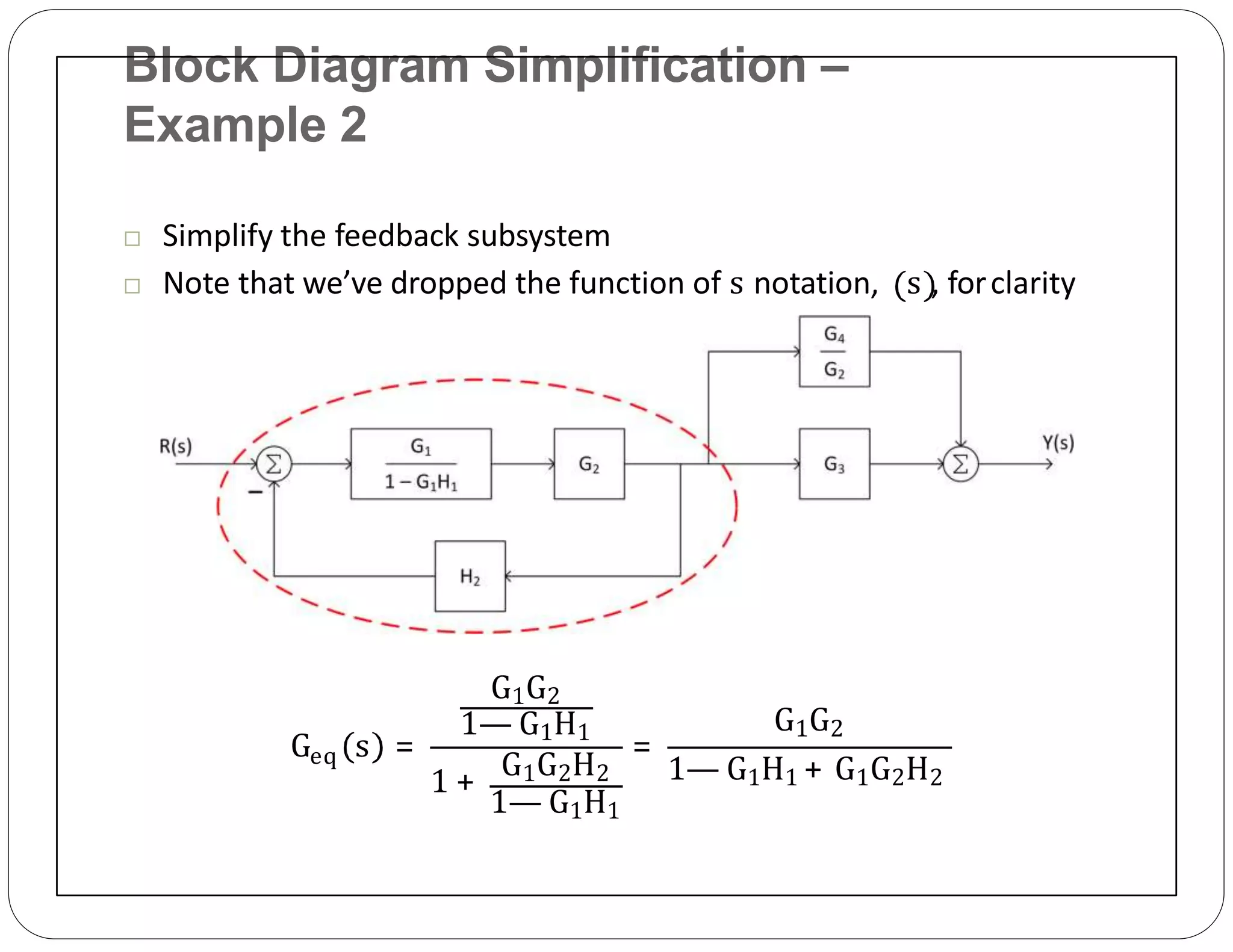
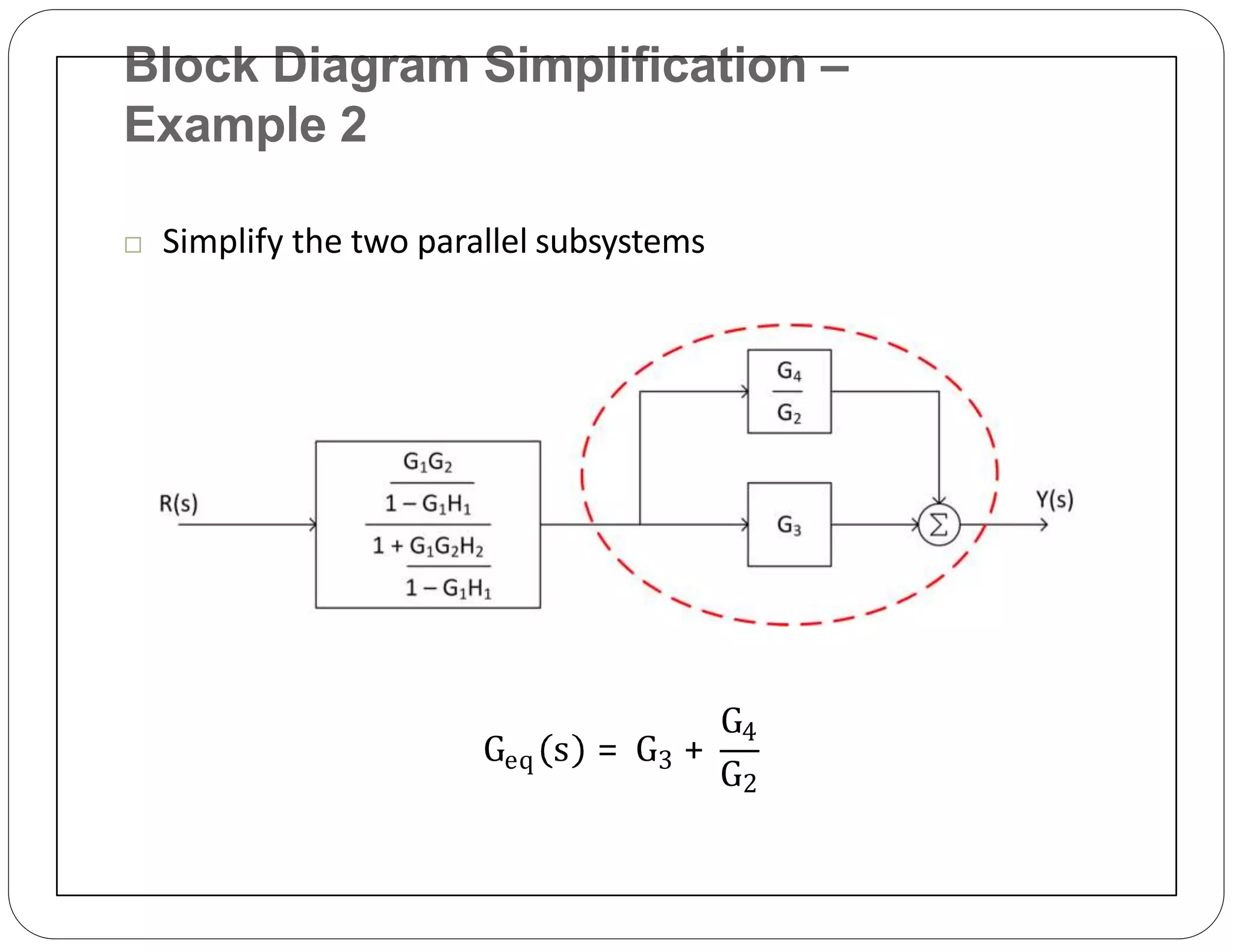
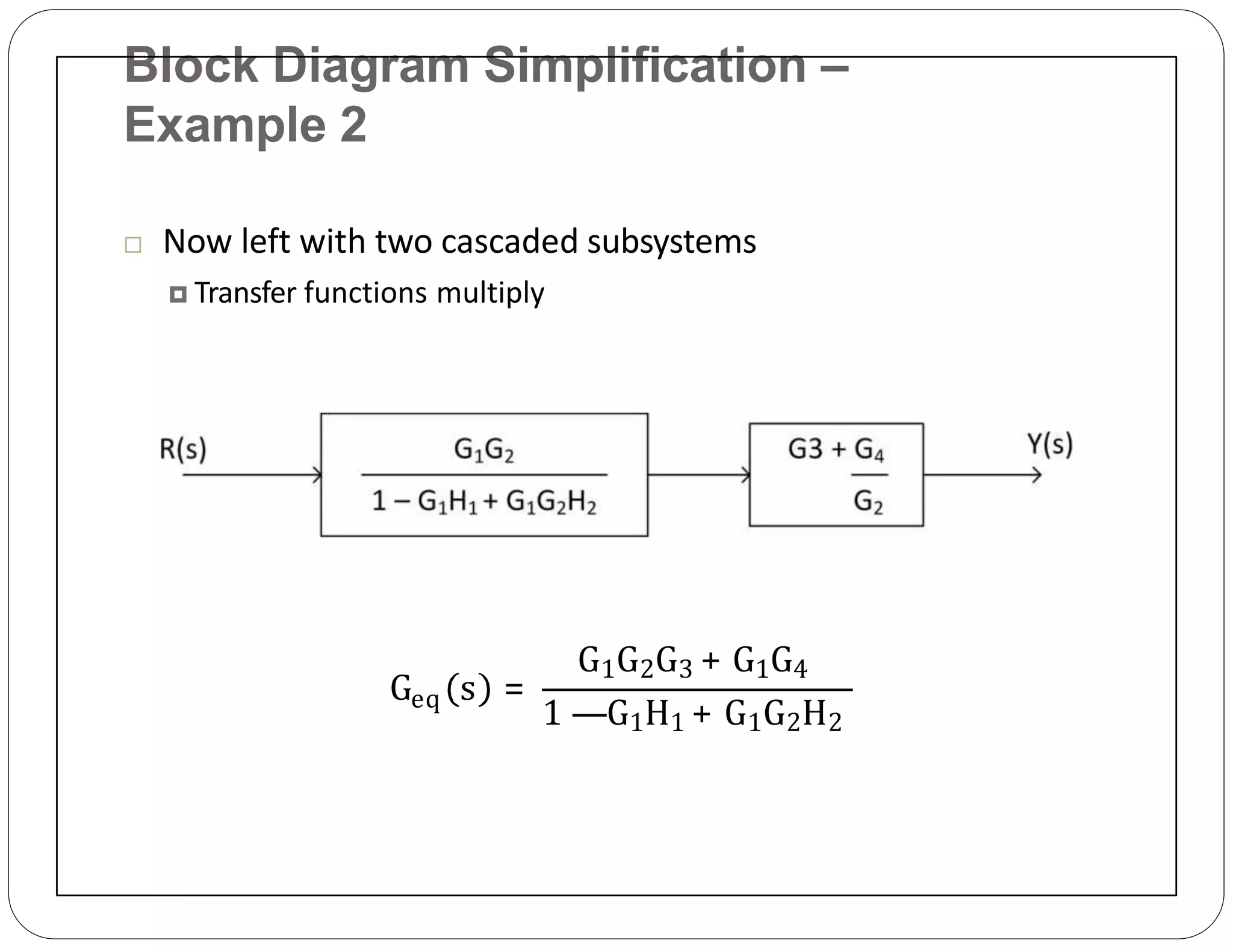
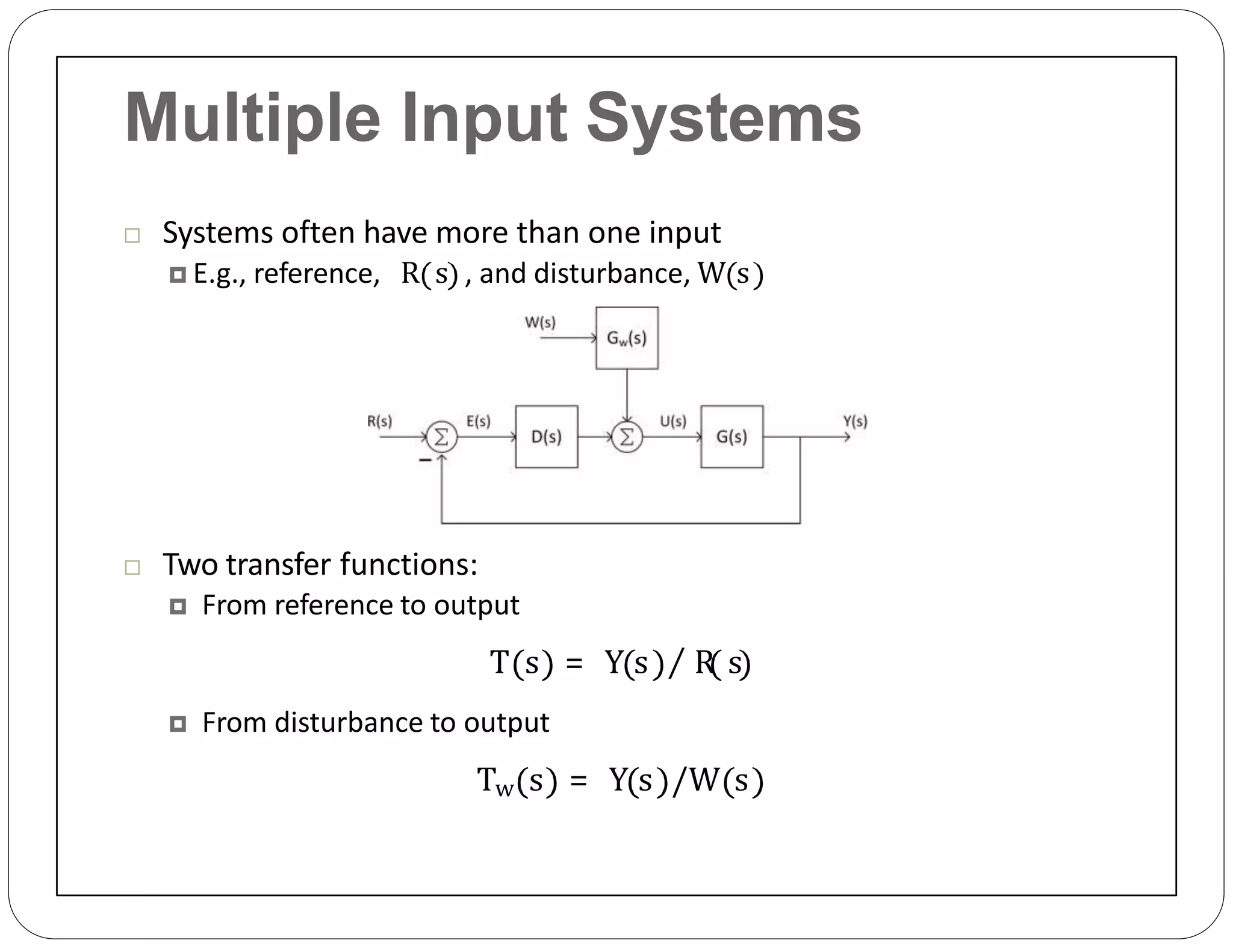
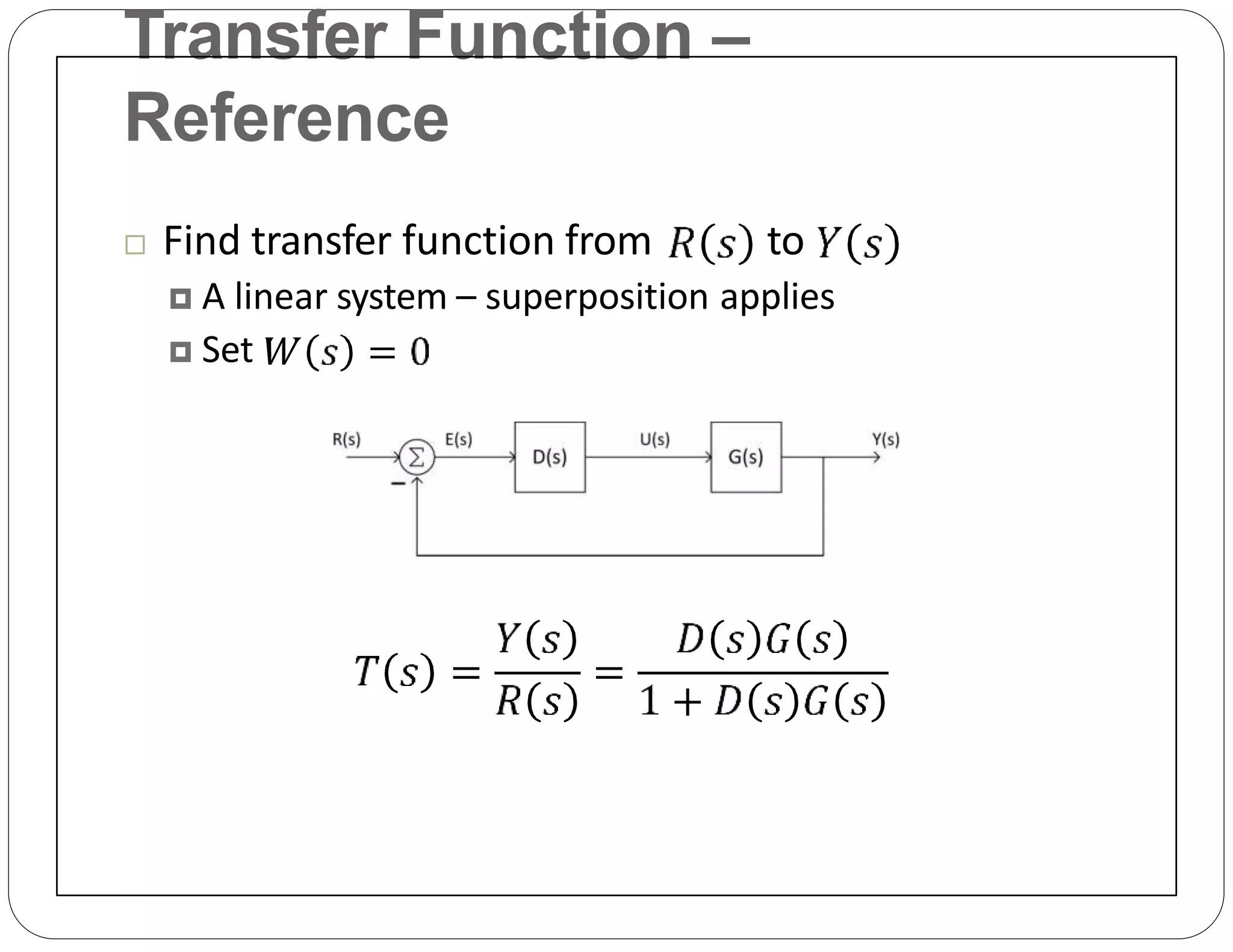
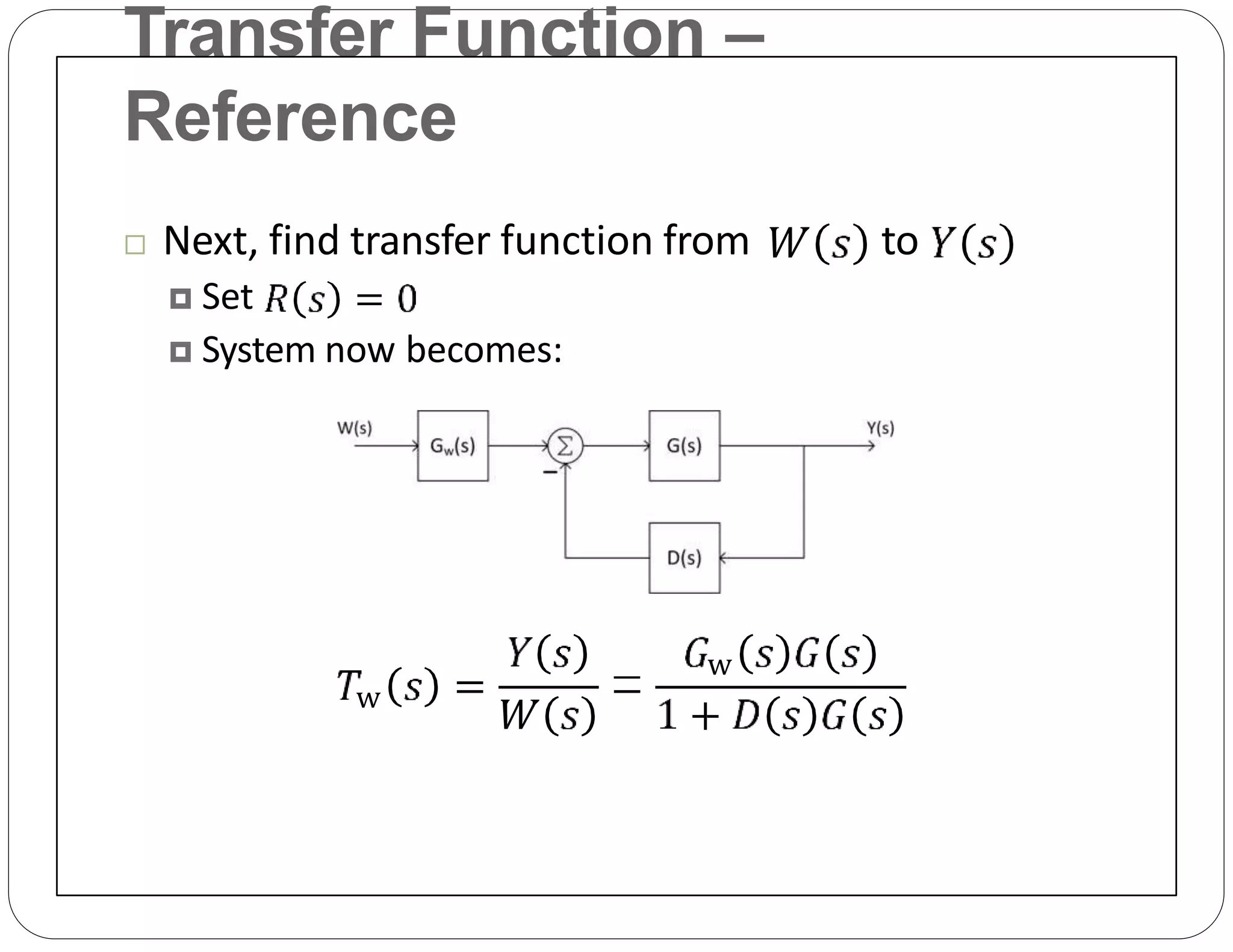
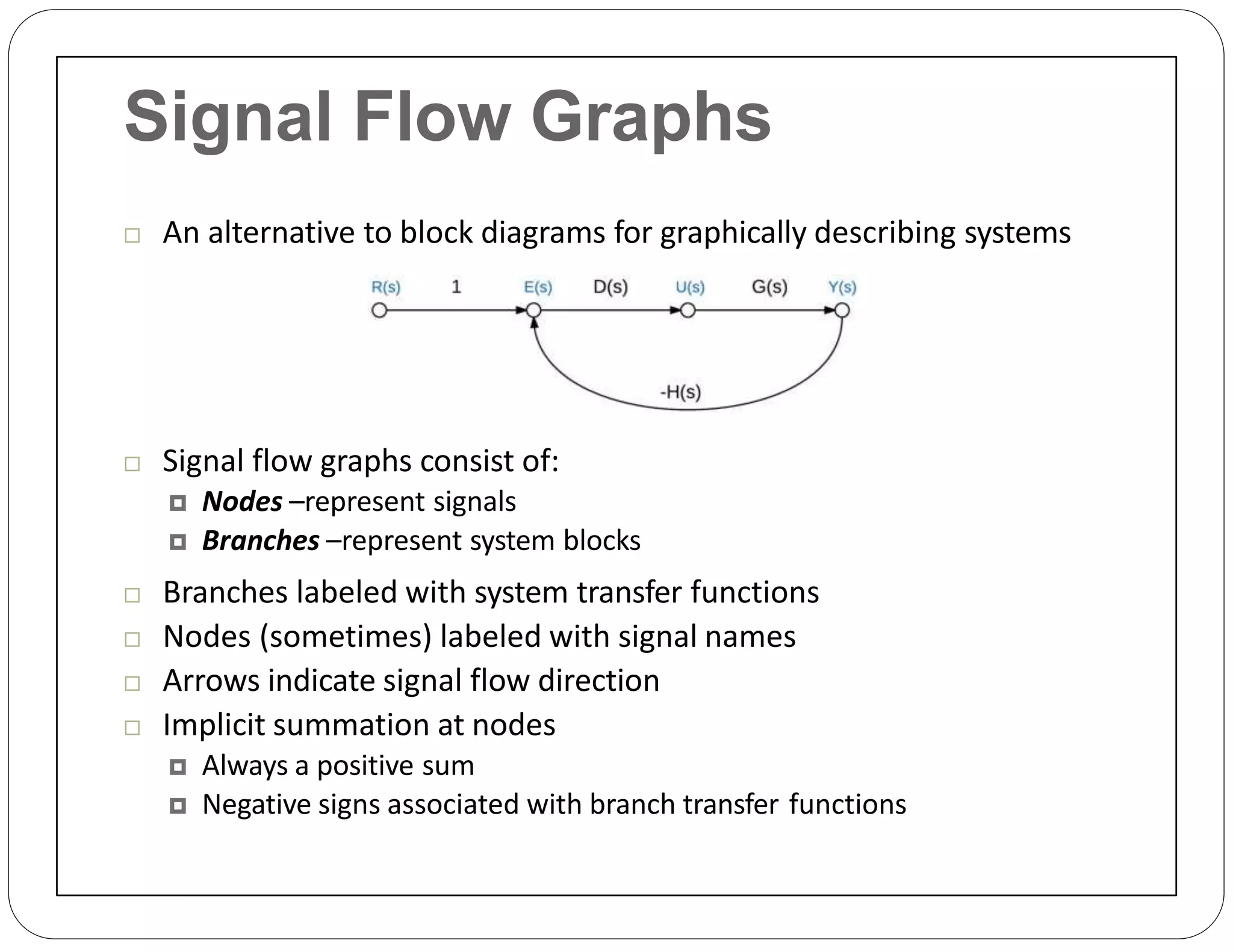
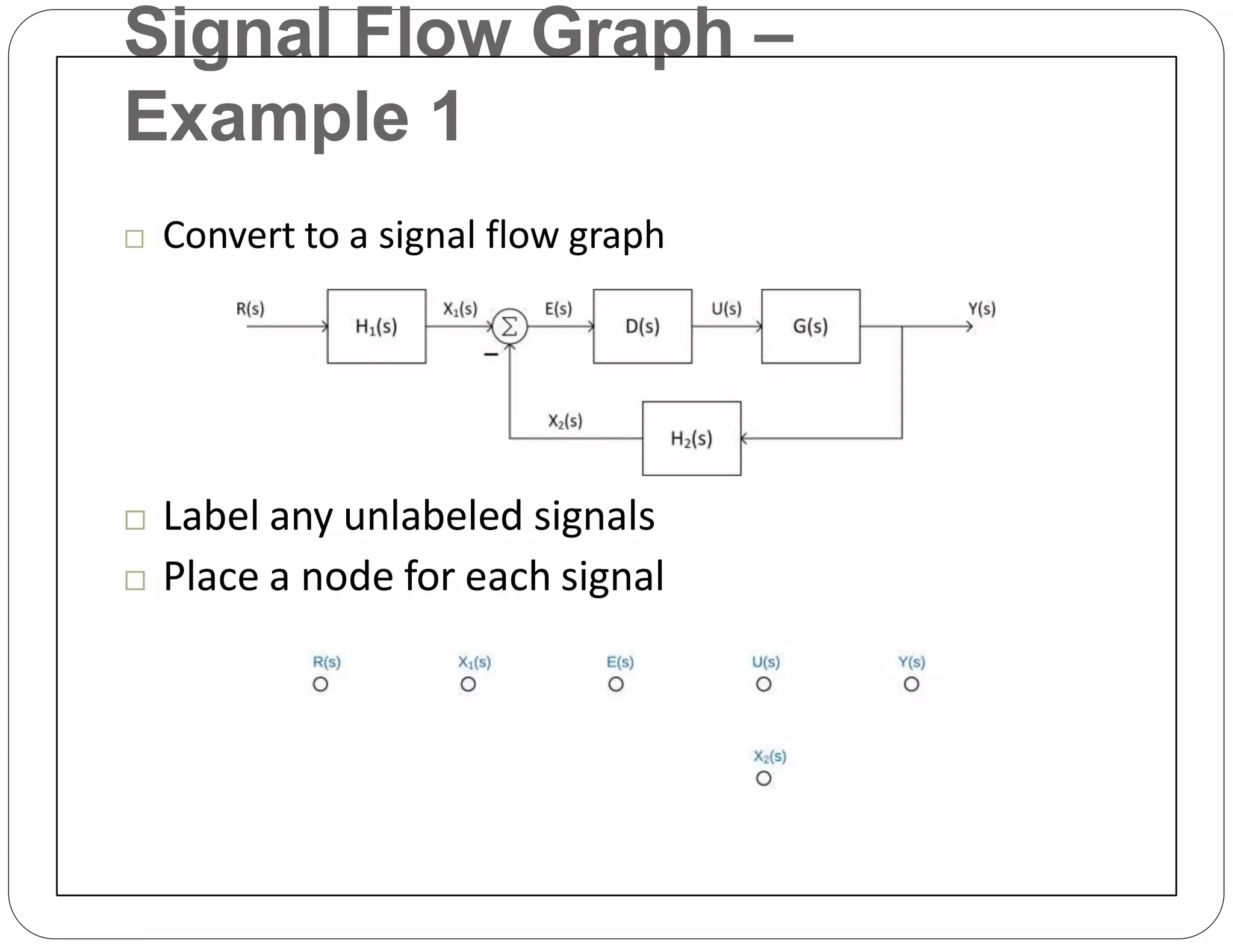
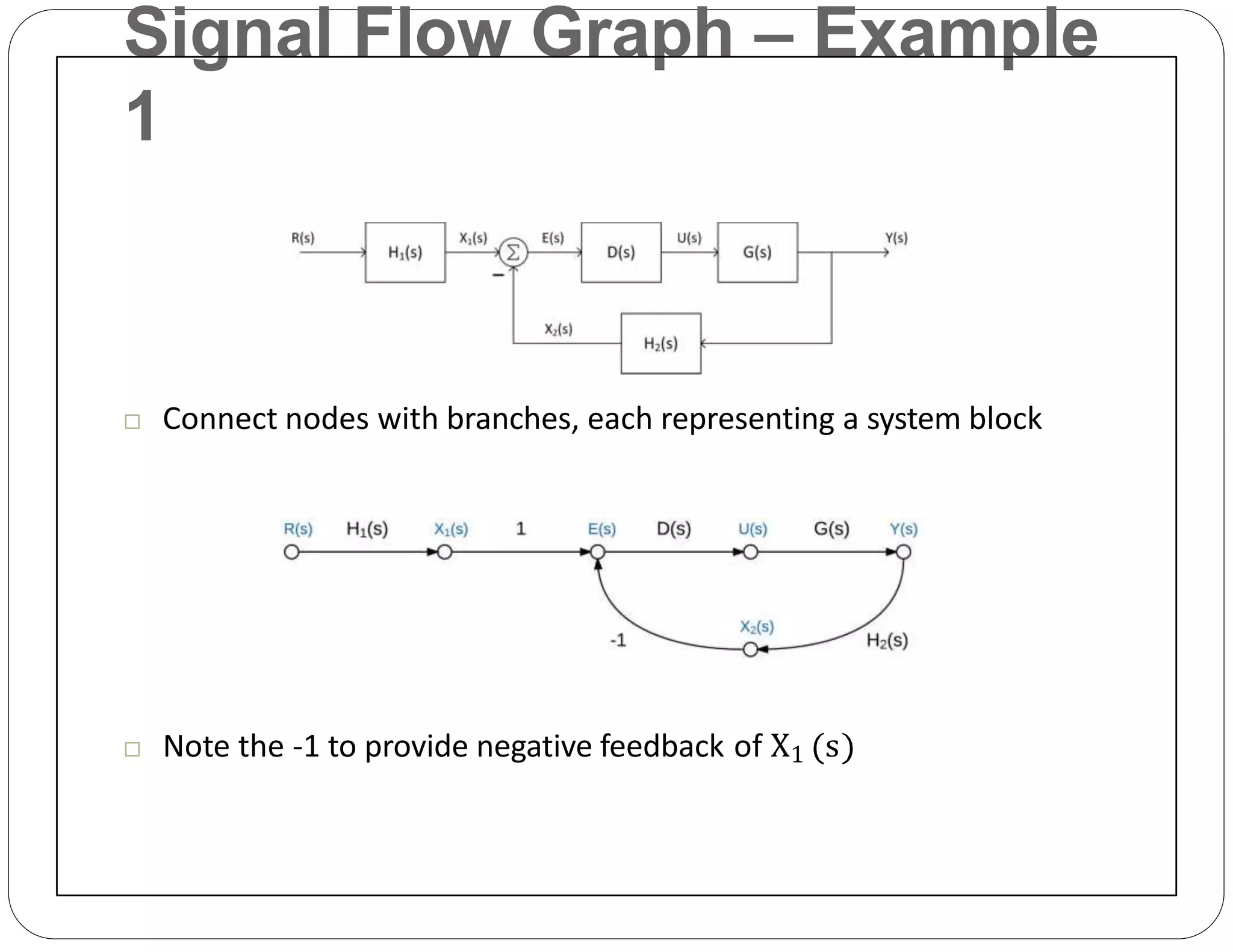
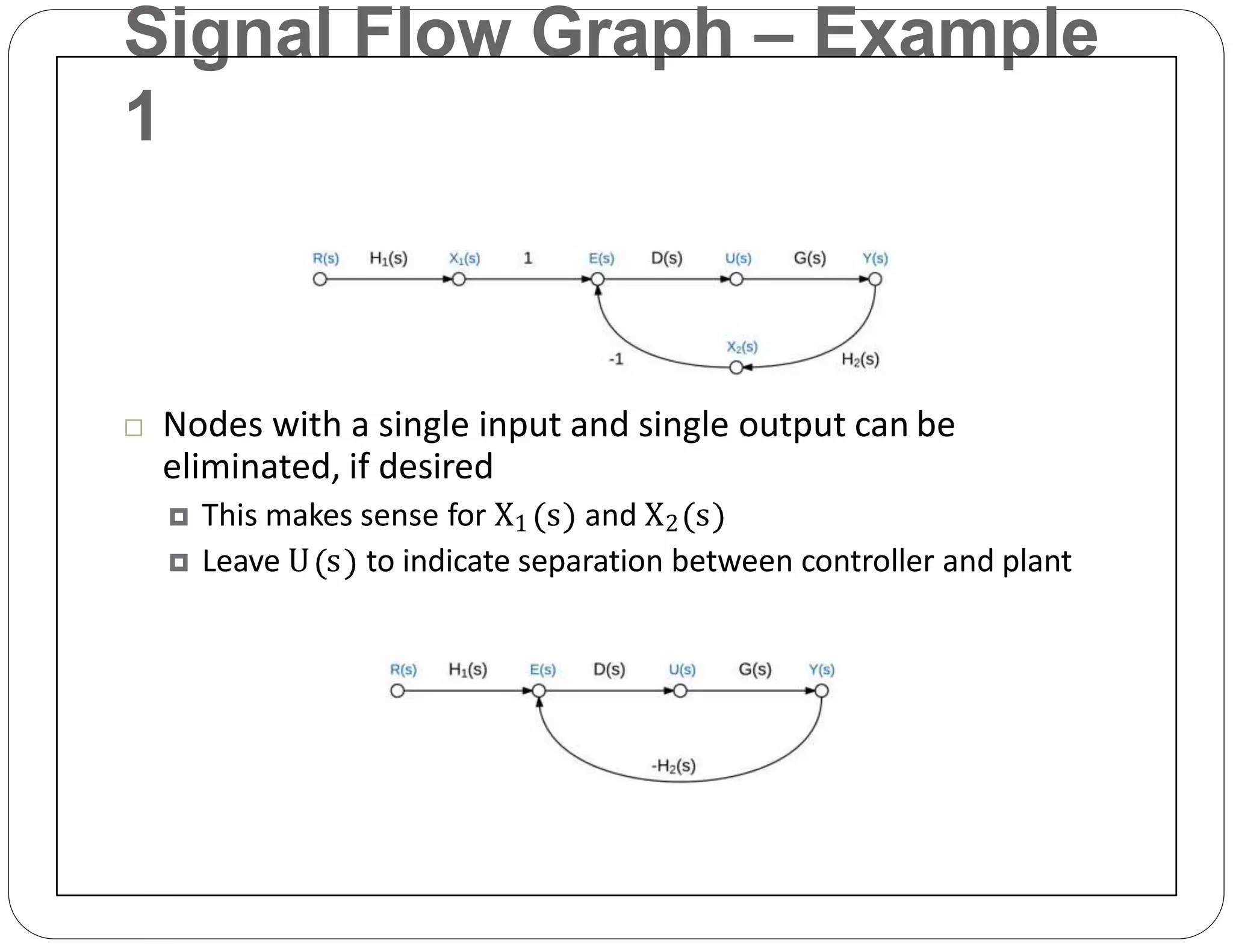
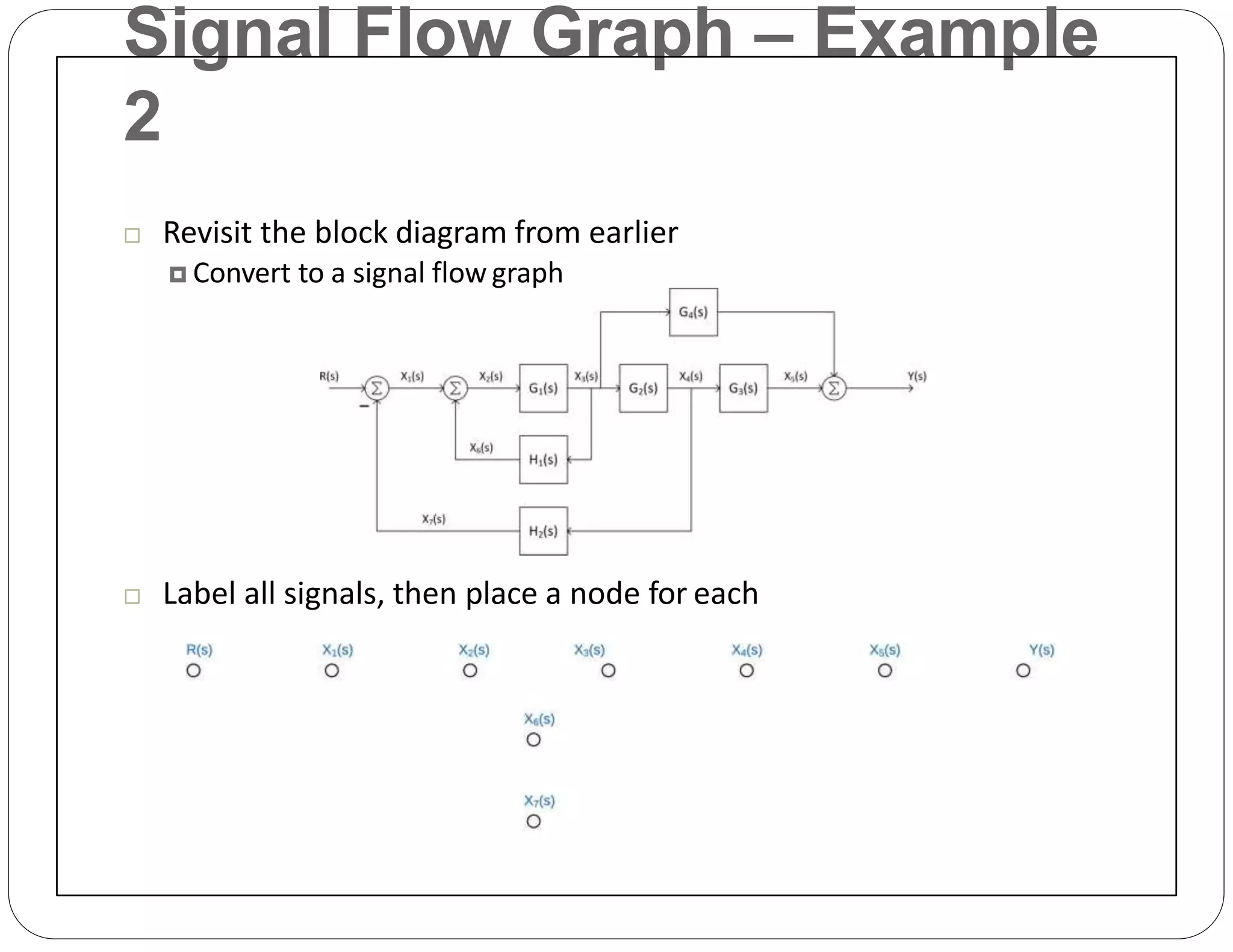
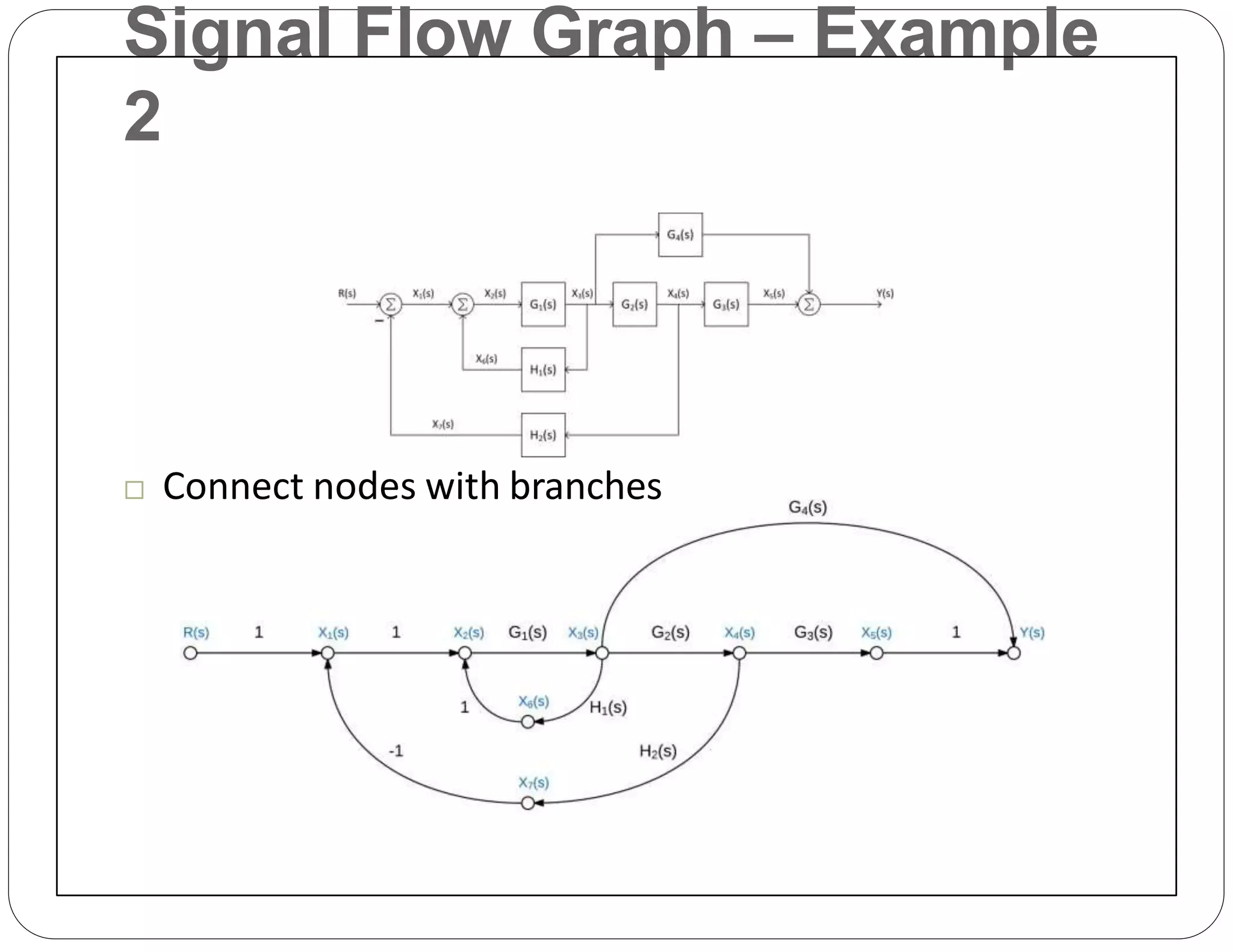
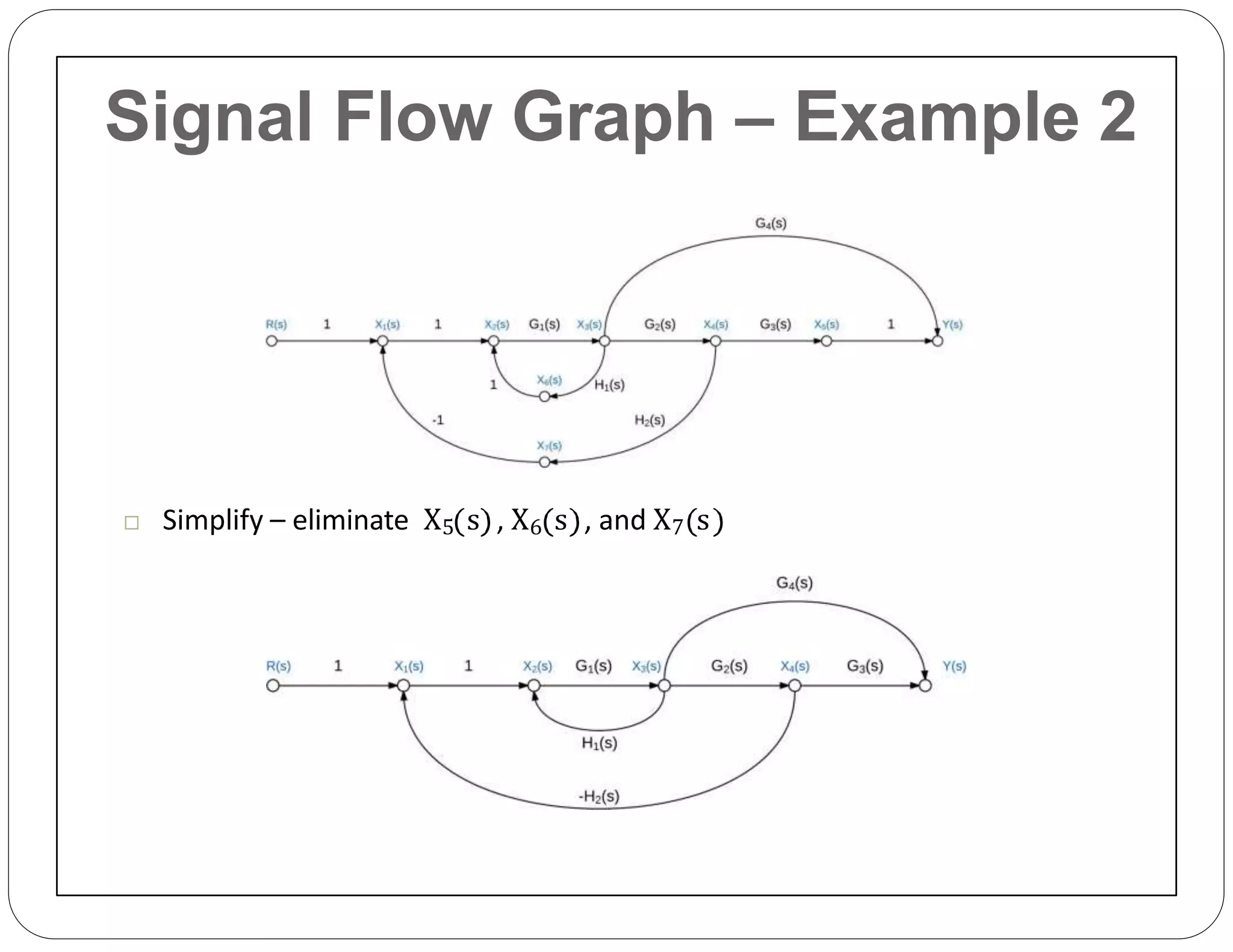
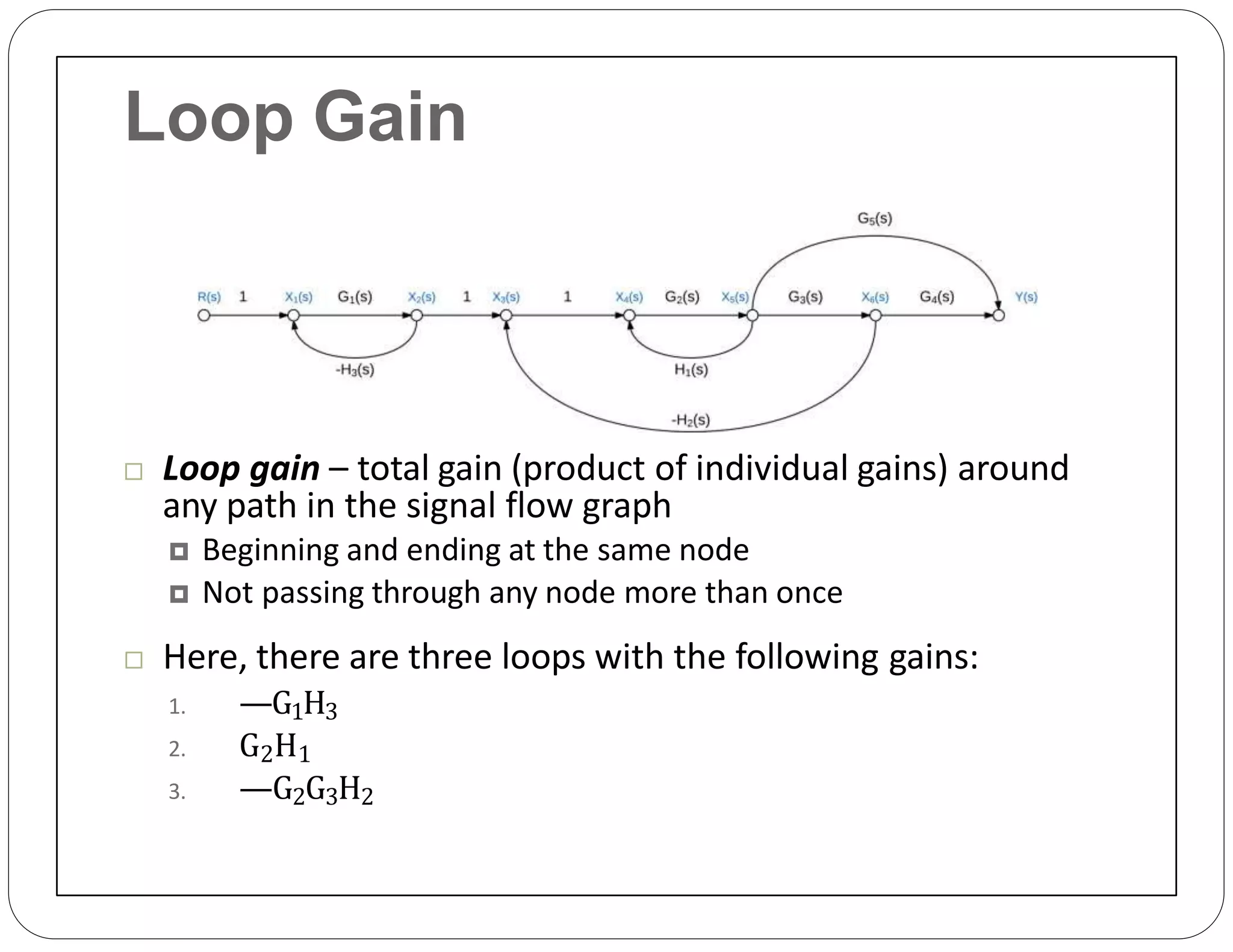
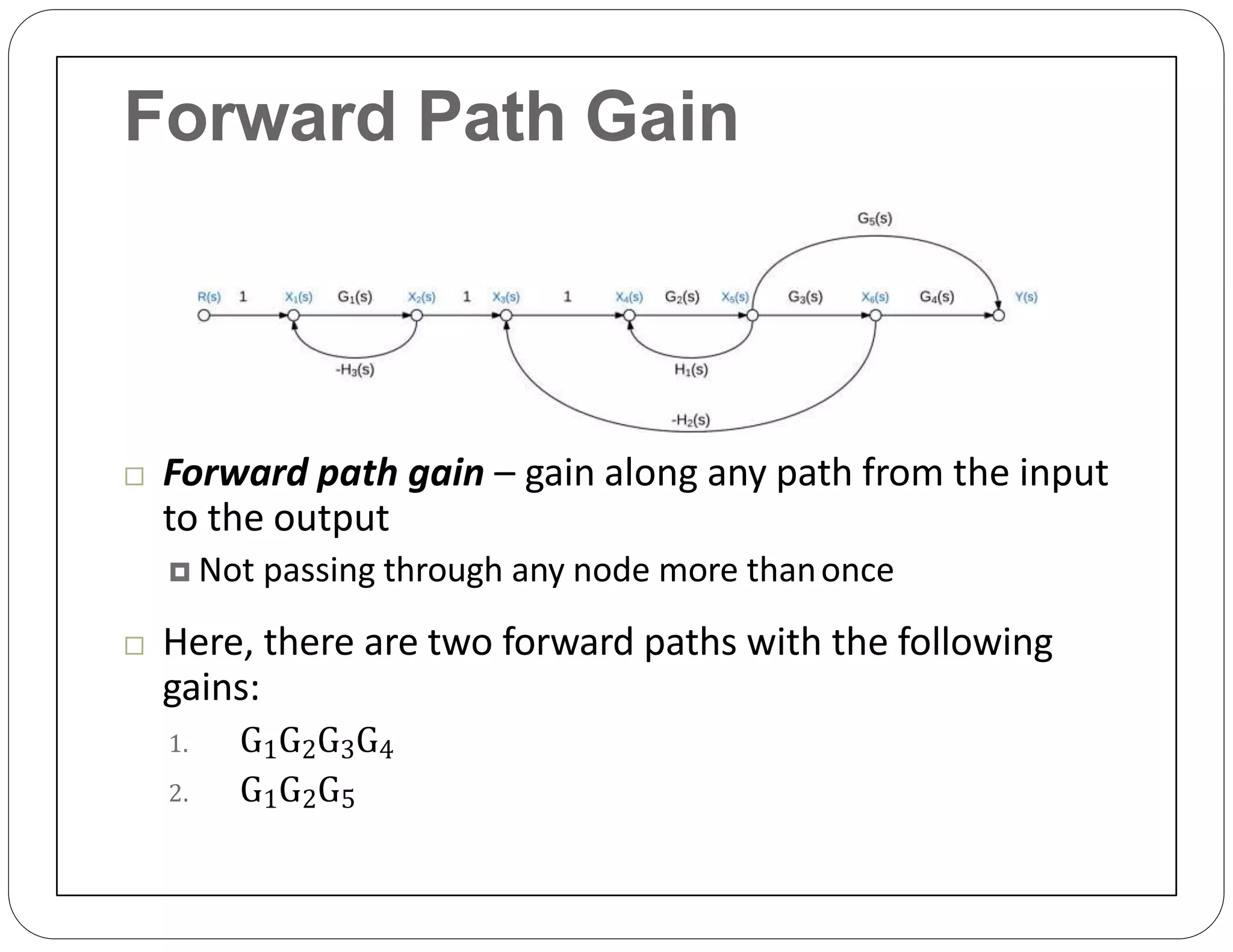
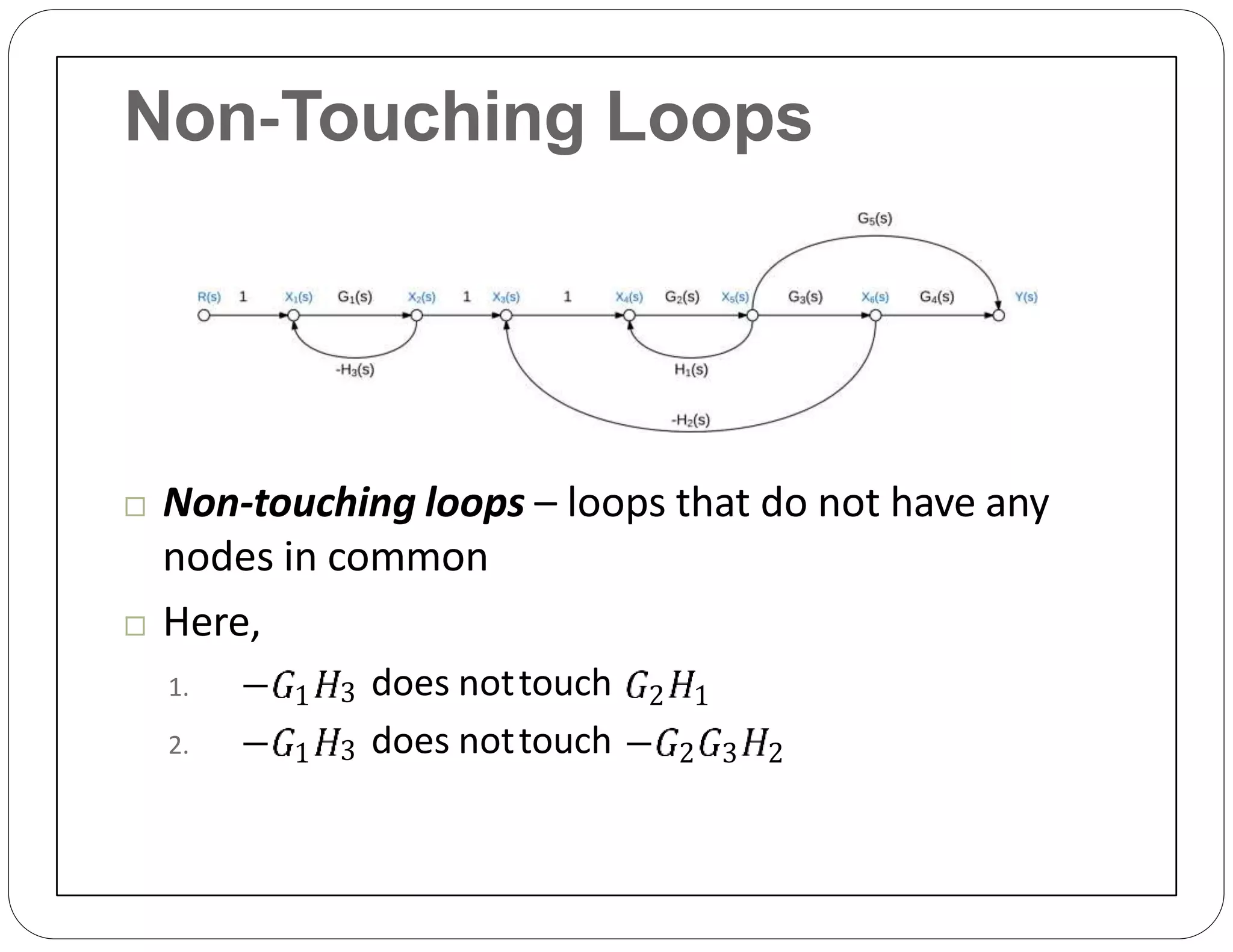
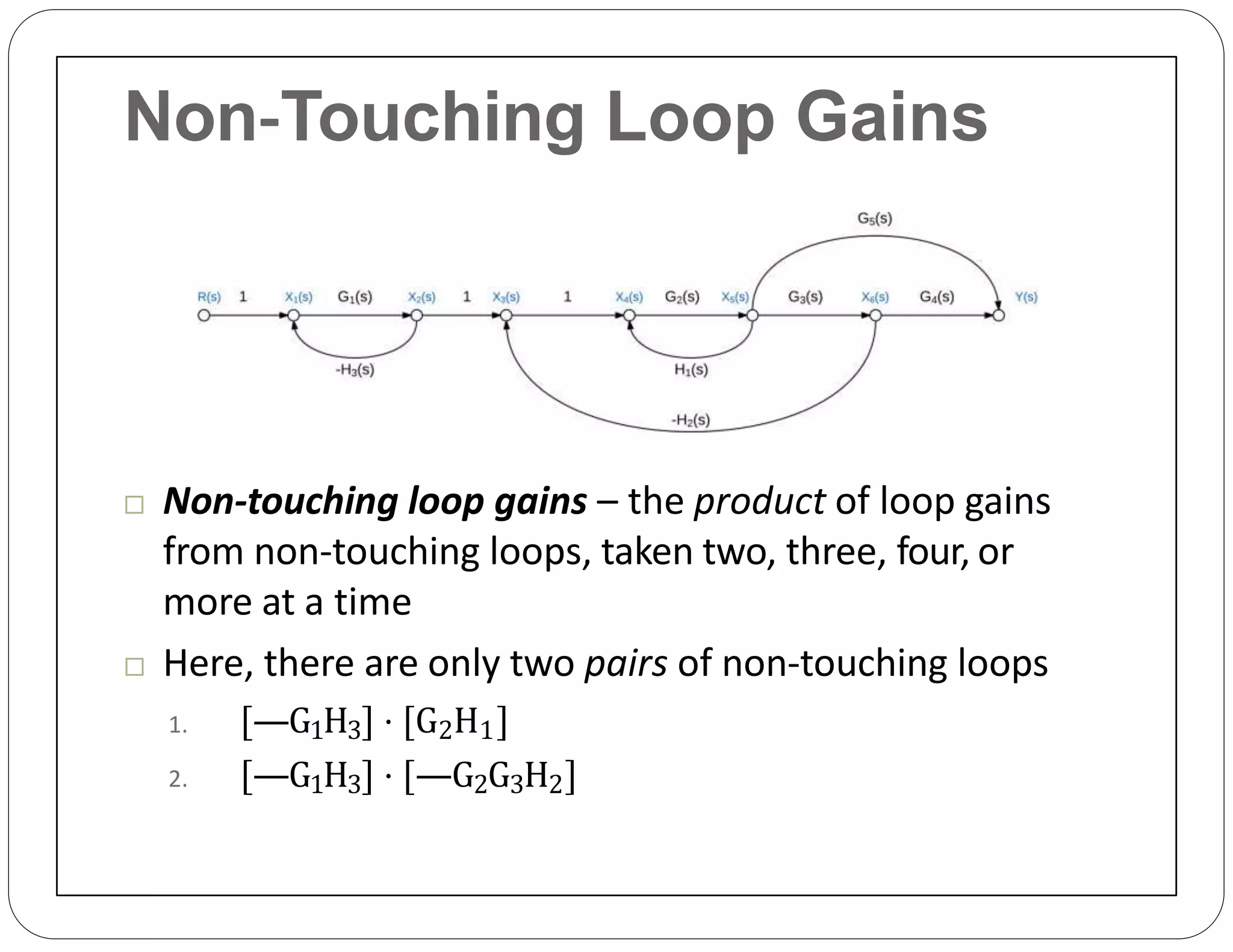
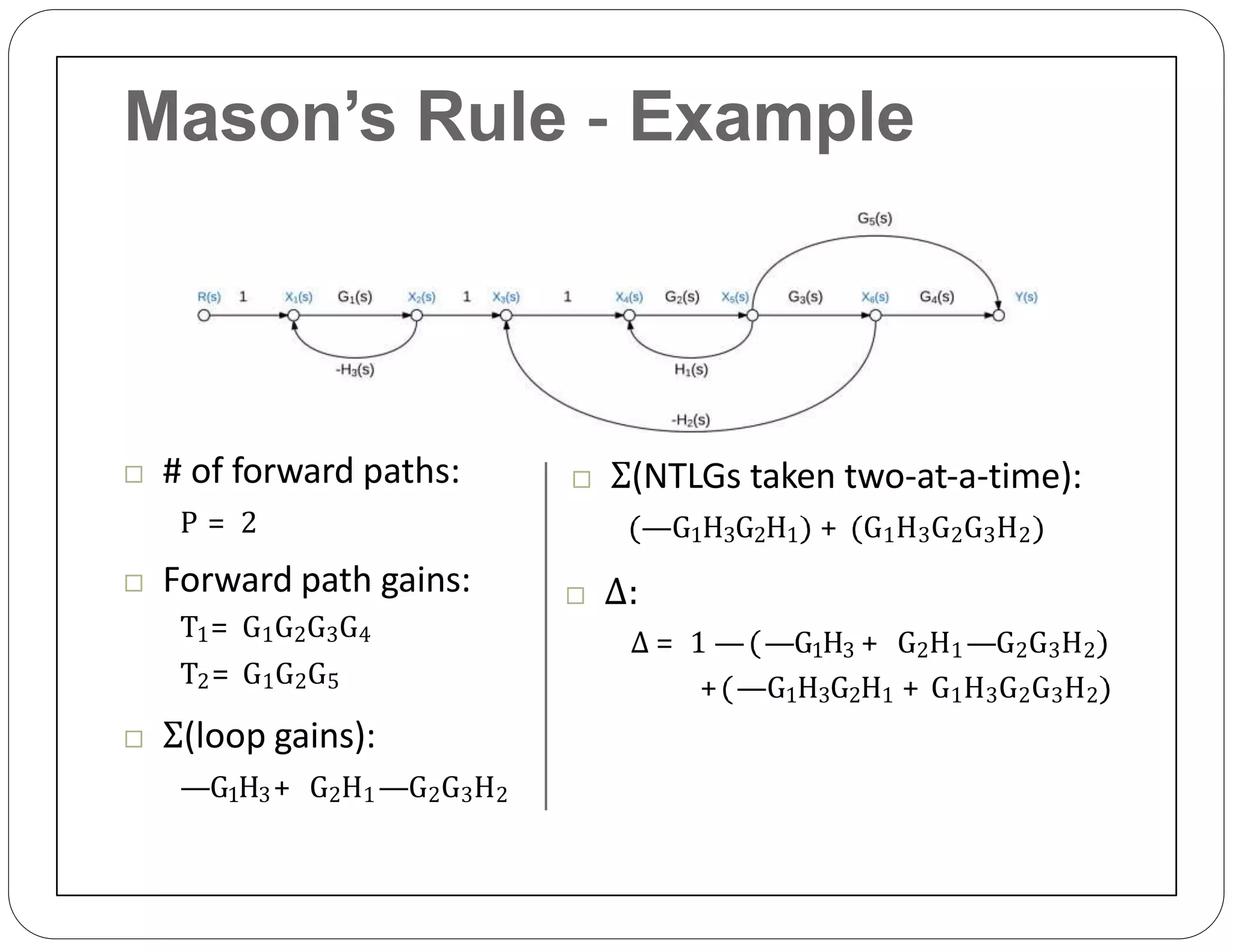
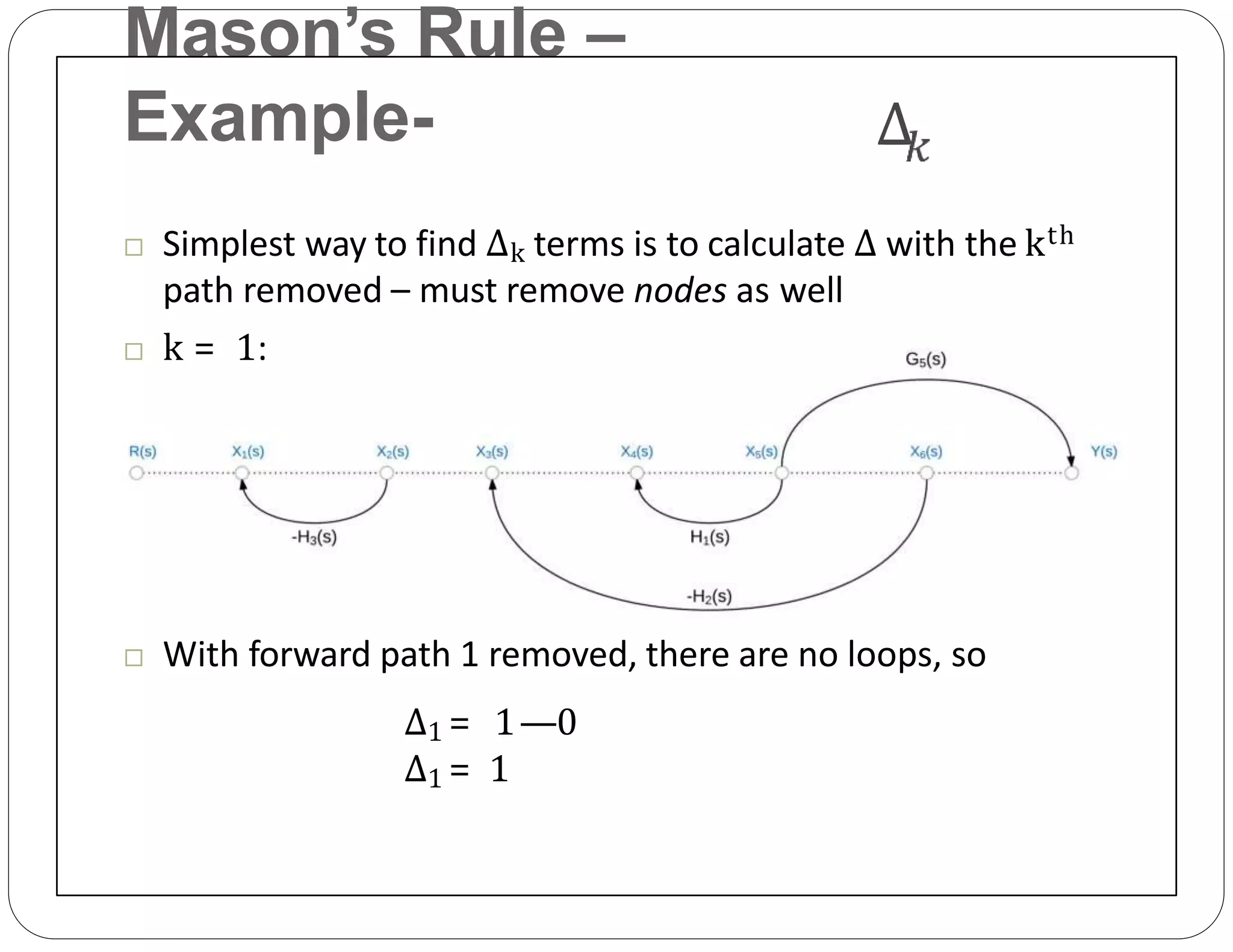
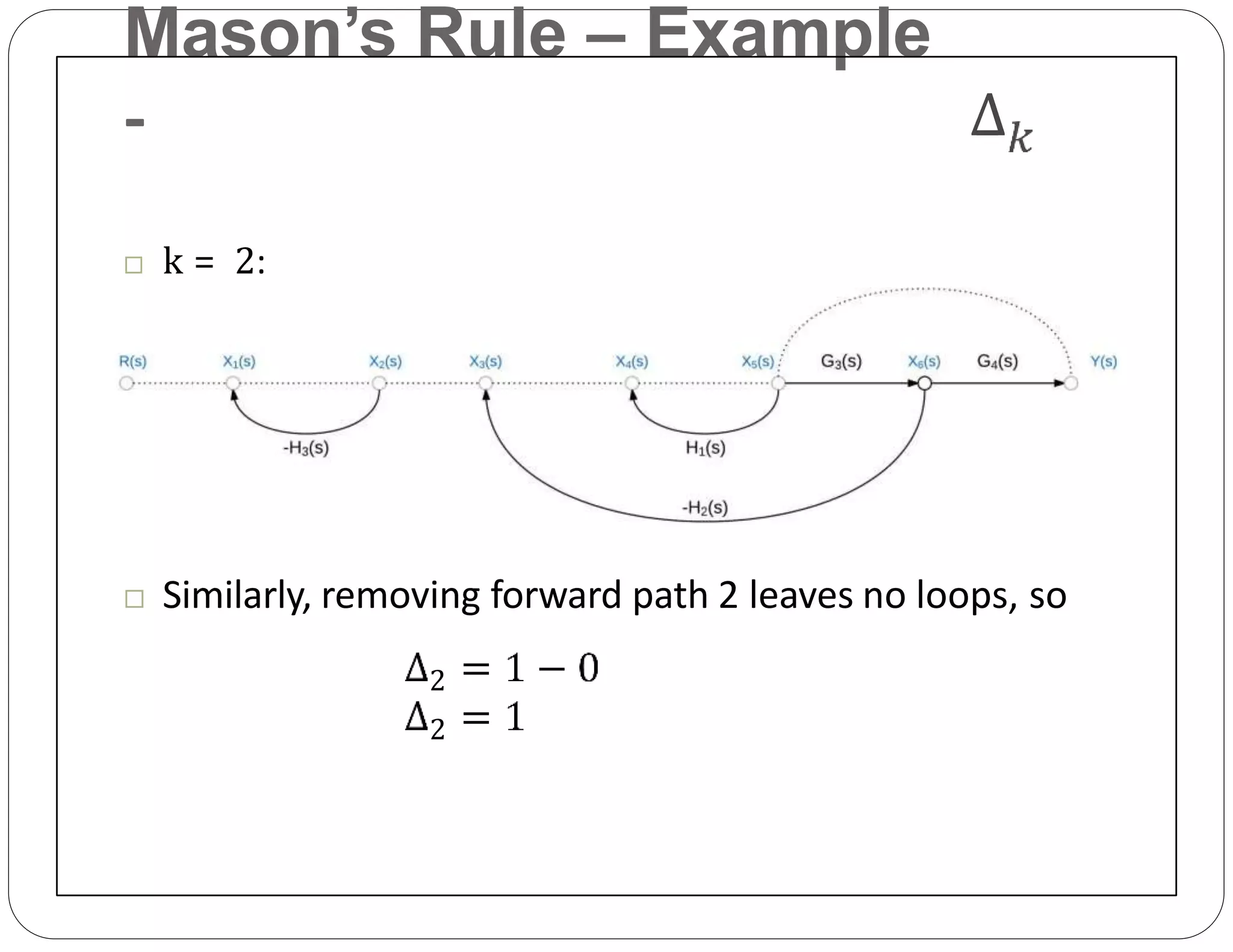
The document provides an overview of block diagrams and signal flow graphs, explaining their components such as blocks, signals, and summing junctions. It discusses the input/output relationships for cascaded, parallel, and feedback configurations, highlighting the importance of transfer functions in these systems. The document also introduces Mason's rule for calculating transfer functions and concludes with examples of block diagram simplification and the conversion to signal flow graphs.

1. Chapter-2:
BLOCK DIAGRAMS & SIGNAL FLOW GRAPHS
Dr.K.Hussain
Associate Professor & Head
Dept. of EE, SITCOE

2. Block Diagram Representation
 In the introductory section we saw examples of block diagrams
to represent systems, e.g.:
 Block diagrams consist of
 Blocks – these represent subsystems – typically modeled by, and labeled
with, a transfer function
 Signals – inputs and outputs of blocks – signal direction indicated by
arrows – could be voltage, velocity, force, etc.
 Summing junctions – points were signals are algebraically summed –
subtraction indicated by a negative sign near where the signal joins the
summing junction

3. Standard Block Diagram
Forms
 The basic input/output relationship for a single block is:
Y s = U s ⋅ G s
 Block diagram blocks can be connected in three basic forms:
 Cascade
 Parallel
 Feedback
 We’ll next look at each of these forms and derive a single‐
block equivalent for each

4. Cascade Form
 Blocks connected in cascade:
X2 s = X1 s ⋅ G2 sX1 s = U s ⋅ G1 s ,
Y s
Y s
= X2 s ⋅ G3 s = X1 s ⋅ G2 s ⋅ G3 s
= U s ⋅ G1 s ⋅ G2 s ⋅ G3 s = U s ⋅ Geq s
Geq s = G1 s ⋅ G2 s ⋅ G3 s
 The equivalent transfer function of cascaded blocks is the
product of the individual transfer functions

5. Parallel Form
 Blocks connected in parallel:
X1 s = U s ⋅ G1 s
X2 s = U s ⋅ G2 s
X3 s = U s ⋅ G3 s
Y s = X1 s ± X2 s ± X3 s
Y s = U s ⋅ G1 s ± U s ⋅ G2 s ± U s ⋅ G3 s
Y s = U s G1 s ± G2 s ± G3 s = U s ⋅ Geq s
Geq s = G1 s ± G2 s ± G3 s
 The equivalent transfer function is the sum of the individual
transfer functions:

6. Feedback Form
 Of obvious interest to us, is the feedback form:
Y s = E s G s
Y s = R s —X s G s
Y s = R s —Y s H s G s
Y s = R s ⋅
Y s 1 + G s H s = R s G s
G s
1 + G s H s
 The closed‐loop transfer function, T s , is
T s ==
Y s G s
R s 1 + G s H s

7. Feedback Form
 Note that this is negative feedback, for positive feedback:
T s =
G s
1— G s H s
 The G s H s factor in the denominator is the loop gain or open‐loop
transfer function
 The gain from input to output with the feedback path broken is the
forward path gain – here, G s
 In general:
T s =
forward path gain
1 —loop gain
T s =
G s
1 + G s H s

8. Closed‐Loop Transfer Function ‐ Example
 Calculate the closed‐loop transfer function
 D s and G s are in cascade
 H1 s is in cascade with the feedback system consisting of D s ,
G s , and H2 s
1T s = H s ⋅
D s G s
1 + D s G s H2 s
T s =
H1 s D s G s
1 + D s G s H2 s

9. Unity‐Feedback
Systems
 We’re often interested in unity‐feedback systems
 Feedback path gain is unity
 Can always reconfigure a system to unity‐feedback form
 Closed‐loop transfer function is:
T s =
D s G s
1 + D s G s

10. Block Diagram Algebra
 Often want to simplify block diagrams into simpler,
recognizable forms
 Todetermine the equivalent transfer function
 Simplify to instances of the three standard forms,
then simplify those forms
 Move blocks around relative to summing junctions
and pickoff points – simplify to a standard form
 Move blocks forward/backward past summing junctions
 Move blocks forward/backward past pickoff points

11. Moving Blocks Back Past a Summing
Junction
 The following two block diagrams are equivalent:
Y s = U1 s + U2 s G s = U1 s G s + U2 s G s

12. Moving Blocks Forward Past a Summing
Junction
 The following two block diagrams are equivalent:
Y s = U1 s G s + U2 s = U1 s + U2 s
1
G s
G s

13. Moving Blocks Relative to Pickoff
Points
 We can move blocks backward past pickoff points:
 And, we can move them forward past pickoff points:

14. Block Diagram Simplification –
Example 1
 Rearrange the following into a unity‐feedback system
 Move the feedback block, H s , forward,
past the summing junction
 Add an inverse block on R s to
compensate for the move
 Closed‐loop transfer function:
T s
1 H s G s
1 + G s H s
=
H s
=
G s
1 + G s H s

15. Block Diagram Simplification –
Example 2
 Find the closed‐loop transfer function of the following
system through block‐diagram simplification

16. Block Diagram Simplification –
Example 2
 G1 s and H1 s are in feedback form
eqG s =
G1 s
1 —G1 s H1 s

17. Block Diagram Simplification –
Example 2
 Move G2 s backward past the pickoff point
become a Block from previous step, G2 s , and H2 s
feedback system that can be simplified

18. Block Diagram Simplification –
Example 2
 Simplify the feedback subsystem
 Note that we’ve dropped the function of s notation, s , forclarity
Geq s =
G1G2
1— G1H1
1 + G1G2H2
1— G1H1
=
G1G2
1— G1H1 + G1G2H2

19. Block Diagram Simplification –
Example 2
 Simplify the two parallel subsystems
eq 3G s = G +
G4
G2

20. Block Diagram Simplification –
Example 2
 Now left with two cascaded subsystems
 Transfer functions multiply
eqG s =
G1G2G3 + G1G4
1 —G1H1 + G1G2H2

21. Block Diagram Simplification –
Example 2
 The equivalent, close‐loop transfer function is
T s =
G1G2G3 + G1G4
1 —G1H1 + G1G2H2

22. Multiple Input Systems
 Systems often have more than one input
 E.g., reference, R s , and disturbance, W s
 Two transfer functions:
 From reference to output
T s = Y s ⁄ R s
 From disturbance to output
Tw s = Y s /W s

23. Transfer Function –
Reference
 Find transfer function from to
 A linear system – superposition applies
 Set

24. Transfer Function –
Reference
to Next, find transfer function from
 Set
 System now becomes:
w
w

25. Multiple Input Systems
 Two inputs, two transfer functions
T s =
D c G c
and Tw s =
Gw c G c
1+D c G c 1+ D c G c
 is the controller transfer function
 Ultimately, we’ll determine this
w We have control over both and
 What do we want these to be?
 Design
 Design w
for desired performance
for disturbance rejection

26. Signal Flow Graphs
 An alternative to block diagrams for graphically describing systems
 Signal flow graphs consist of:
 Nodes –represent signals
 Branches –represent system blocks
 Branches labeled with system transfer functions
 Nodes (sometimes) labeled with signal names
 Arrows indicate signal flow direction
 Implicit summation at nodes
 Always a positive sum
 Negative signs associated with branch transfer functions

27. Block Diagram Signal Flow
Graph
 Toconvert from a block diagram to a signal flow
graph:
1. Identify and label all signals on the block diagram
2. Place a node for each signal
3. Connect nodes with branches in place of the blocks
 Maintain correct direction
 Label branches with corresponding transfer functions
 Negate transfer functions as necessary to provide negative
feedback
4. If desired, simplify where possible

28. Signal Flow Graph –
Example 1
 Convert to a signal flow graph
 Label any unlabeled signals
 Place a node for each signal

29. Signal Flow Graph – Example
1
 Connect nodes with branches, each representing a system block
 Note the ‐1 to provide negative feedback of X1 s

30. Signal Flow Graph – Example
1
 Nodes with a single input and single output can be
eliminated, if desired
 This makes sense for X1 s and X2 s
 Leave U s to indicate separation between controller and plant

31. Signal Flow Graph – Example
2
 Revisit the block diagram from earlier
 Convert to a signal flow graph
 Label all signals, then place a node for each

32. Signal Flow Graph – Example
2
 Connect nodes with branches

33. Signal Flow Graph – Example 2
 Simplify – eliminate X5 s , X6 s , and X7 s

34. Signal Flow Graphs vs. Block
Diagrams
 Signal flow graphs and block diagrams are
alternative, though equivalent, tools for graphical
representation of interconnected systems
 A generalization (not a rule)
 Signal flow graphs – more often used when dealing
with state‐space system models
 Block diagrams – more often used when dealing with
transfer function system models

35. Mason’s Rule
 We’ve seen how to reduce a complicated block
diagram to a single input‐to‐output transfer function
 Many successive simplifications
 Mason’s rule provides a formula to calculate the same
overall transfer function
 Single application of the formula
 Can get complicated
 Before presenting the Mason’s rule formula, we need
to define some terminology

36. Loop Gain
 Loop gain – total gain (product of individual gains) around
any path in the signal flow graph
 Beginning and ending at the same node
 Not passing through any node more than once
 Here, there are three loops with the following gains:
1. —G1H3
2. G2H1
3. —G2G3H2

37. Forward Path Gain
 Forward path gain – gain along any path from the input
to the output
 Not passing through any node more thanonce
 Here, there are two forward paths with the following
gains:
1. G1G2G3G4
2. G1G2G5

38. Non‐Touching Loops
 Non‐touching loops – loops that do not have any
nodes in common
 Here,
1.
2.
1
1
3 does nottouch
3 does nottouch
2 1
2 3 2

39. Non‐Touching Loop Gains
 Non‐touching loop gains – the product of loop gains
from non‐touching loops, taken two, three, four, or
more at a time
 Here, there are only two pairs of non‐touching loops
1. —G1H3 ⋅ G2H1
2. —G1H3 ⋅ —G2G3H2

40. Mason’s Gain
Formula
T s
R s
=
Y s 1
=
Δ
Σ PkΔk
P
k =1
where
P = # of forwardpaths
Pk = gain of the kth forward path
Δ = 1 —Σ(loopgains)
+Σ(non‐touching loop gains taken two‐at‐a‐time)
—Σ(non‐touching loop gains taken three‐at‐a‐time)
+Σ(non‐touching loop gains taken four‐at‐a‐time)
—Σ…
Δk = Δ —Σ(loop gain terms in Δ that touch the kth forward path)

41. Mason’s Rule ‐ Example
 # of forward paths:
P = 2
 Forward path gains:
T1= G1G2G3G4
T2= G1G2G5
 Σ(loop gains):
—G1H3+ G2H1—G2G3H2
 Σ(NTLGs taken two‐at‐a‐time):
—G1H3G2H1 + G1H3G2G3H2
 Δ:
Δ = 1 — —G1H3 + G2H1—G2G3H2
+ —G1H3G2H1 + G1H3G2G3H2

42. Mason’s Rule –
Example-
 Simplest way to find Δk terms is to calculate Δ with the kth
path removed – must remove nodes as well
 k = 1:
 With forward path 1 removed, there are no loops, so
Δ1 = 1—0
Δ1 = 1

43. Mason’s Rule – Example
‐
 k = 2:
 Similarly, removing forward path 2 leaves no loops, so
2
2

44. Mason’s Rule ‐ Example
 For our example:
P = 2
P1= G1G2G3G4
P2= G1G2G5
Δ = 1 + G1H3 —G2H1 + G2G3H2 —G1H3G2H1 + G1H3G2G3H2
Δ1 = 1
Δ2 = 1
 The closed‐loop transfer function:
T s =
P1Δ1 + P2Δ2
Δ
T s =
G1G2G3G4 + G1G2G5
1 + G1H3 —G2H1 + G2G3H2 —G1H3G2H1 + G1H3G2G3H2
T s =
R s
Y s 1
=
Δ
Σ PkΔk
P
k =1