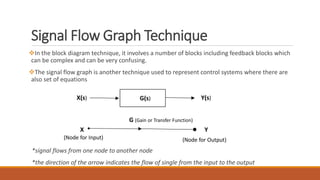
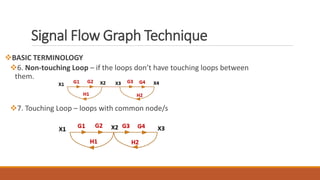
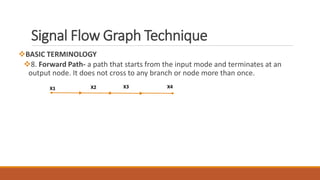
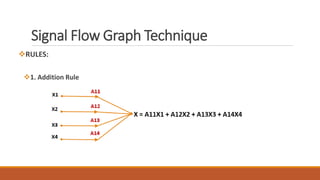
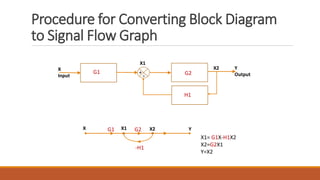
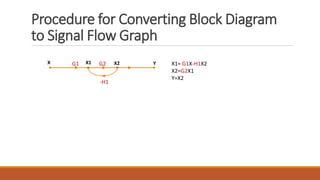
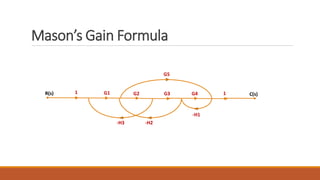
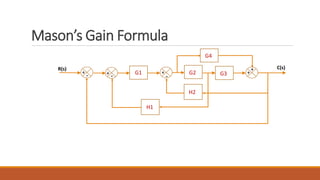
The document discusses signal flow graph techniques for representing and analyzing feedback control systems. It defines key signal flow graph terminology like nodes, loops, and paths. It also outlines rules for constructing a signal flow graph from a block diagram, including the addition, series connection, and transmission rules. Finally, it introduces Mason's Gain Formula for calculating the overall gain of a system from its signal flow graph representation.

1. Feedback and Control
Systems
SIGNAL FLOW GRAPH

2. Signal Flow Graph Technique
In the block diagram technique, it involves a number of blocks including feedback blocks which
can be complex and can be very confusing.
The signal flow graph is another technique used to represent control systems where there are
also set of equations
*signal flows from one node to another node
*the direction of the arrow indicates the flow of single from the input to the output
X(s) Y(s)G(s)
X Y
G (Gain or Transfer Function)
(Node for Input) (Node for Output)

3. Signal Flow Graph Technique
BASIC TERMINOLOGY
1. Node – a point that is used to represent a summing point, take off point or
any variable
2. Input Node – the source of outgoing signals
3. Output Node – (aka sink node) the node that receives the incoming signals
4. Mixed Node – the combination of both the input and output node
5. Loop – the closed path that starts from a node and terminates at the same
node
X1 X2
G1 G2
H
X1 X2G1 G2
H
Loop Not a Loop

4. Signal Flow Graph Technique
BASIC TERMINOLOGY
6. Non-touching Loop – if the loops don’t have touching loops between
them.
7. Touching Loop – loops with common node/s
X1 X2G1 G2
H1
X3G3 G4
H2

5. Signal Flow Graph Technique
BASIC TERMINOLOGY
8. Forward Path- a path that starts from the input mode and terminates at an
output node. It does not cross to any branch or node more than once.
X1 X3X2 X4

6. Signal Flow Graph Technique
RULES:
1. Addition Rule

7. Signal Flow Graph Technique
RULES:
2. Series Connection
3. Transmission Rule
X1 X3X2H1 H2
X1 X3H1H2
X
X1
X2
A11
A12
X1 = A11X
X2 = A12X

8. Procedure for Converting Block Diagram
to Signal Flow Graph
 Step 1: Represent all of the summing points, take-off points, input and output and
other variables by nodes.
Step 2: Draw an arrow on the branches connecting the nodes and write gain or
transmittance or transfer function of block over the arrow. The flow of signals is known
by the direction of the arrows.
Step 3: Represent all the feedback systems in the same way and also put the sign ( +/-)
with the transmittance (or Transfer Function) of each feedback block.

9. Procedure for Converting Block Diagram
to Signal Flow Graph
G1 G2
H1
+
-
X
Input
X1
X2 Y
Output
X X2X1 YG1 G2
-H1
X1= G1X-H1X2
X2=G2X1
Y=X2

10. Procedure for Converting Block Diagram
to Signal Flow Graph
X X2X1 YG1 G2
-H1
X1= G1X-H1X2
X2=G2X1
Y=X2

11. Mason’s Gain Formula
𝑇 = ( 𝑘=1
𝑘
𝑃𝑘∆𝑘 ) / ∆
T= The overall transmittance or gain of the system
∆ (𝐺𝑟𝑎𝑝ℎ 𝐷𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎𝑛𝑡)= 1- (sum of the gain product of all possible combination of two non-touching
loops)-(sum of the gain product of all combination of three non-touching loops)+….
Pk= Gain of the kth forward path
∆𝒌= same as ∆ but formed by loops not touching the kth forward path; 1- (sum of gain of all loops which
are not touching the kth forward path)

12. Mason’s Gain Formula
R(s) C(s)1 G1 G2 G3 G4
G5
1
-H1
-H2-H3

13. Mason’s Gain Formula
G1
G4
H2
+
-
R(s)
+
- +
- G2 G3 +
H1
C(s)+

14. Application of Mason’s Gain Formula to
Electrical Network
General procedure to solve the electrical network using the Mason’s Gain Formula:
1. Determine the Laplace transform of the given network and redraw in the s-domain.
2. Write down the equations for the different branch currents and node voltages.
3. Simulate each equation by drawing the corresponding signal flow graph.
4. Combine all signal flow graphs to get the total signal flow of the given network.
5. Use Mason’s gain Formula to derive the transfer function of the given network.
Example: Find the transfer function of the given electrical network.