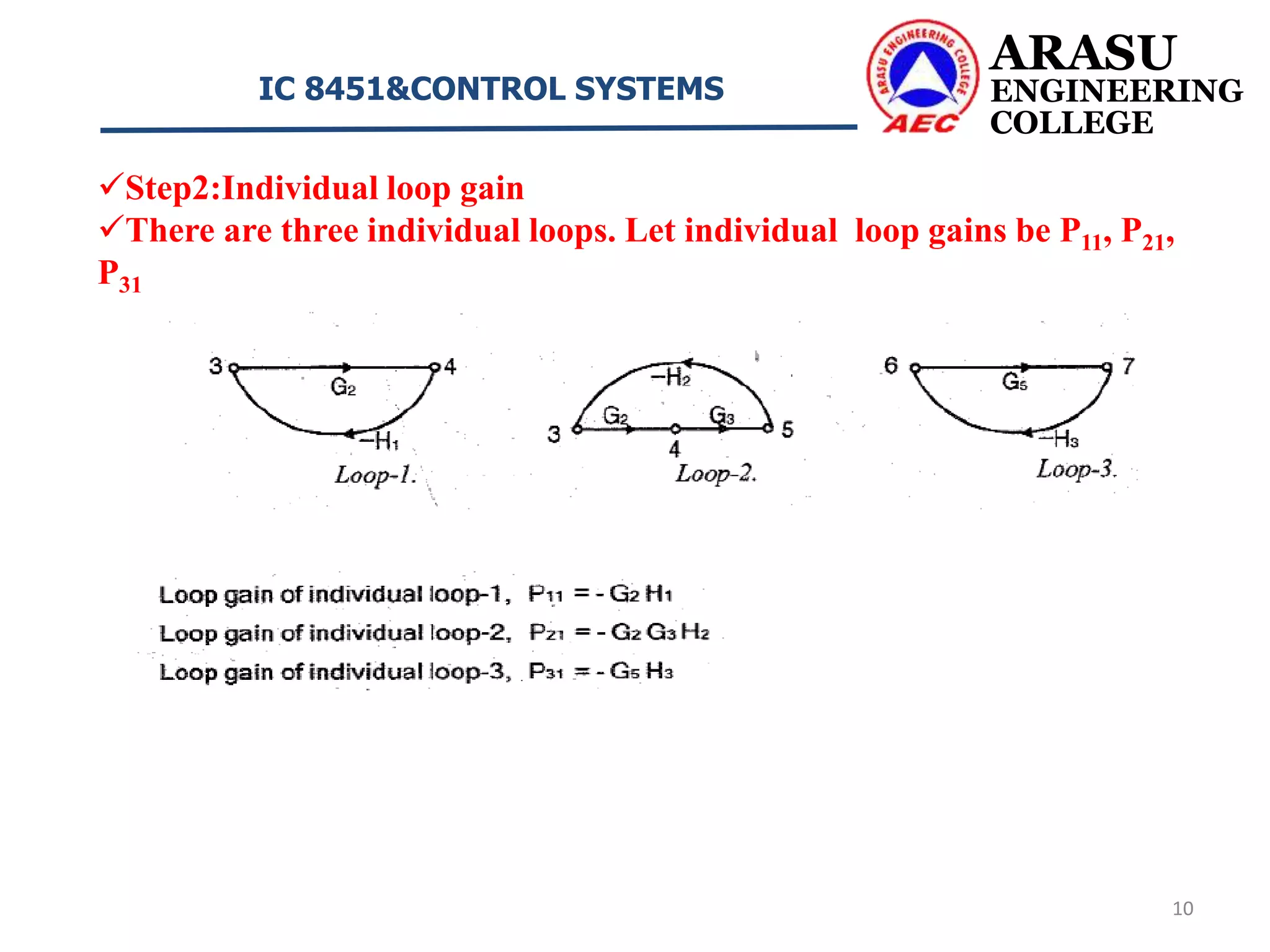
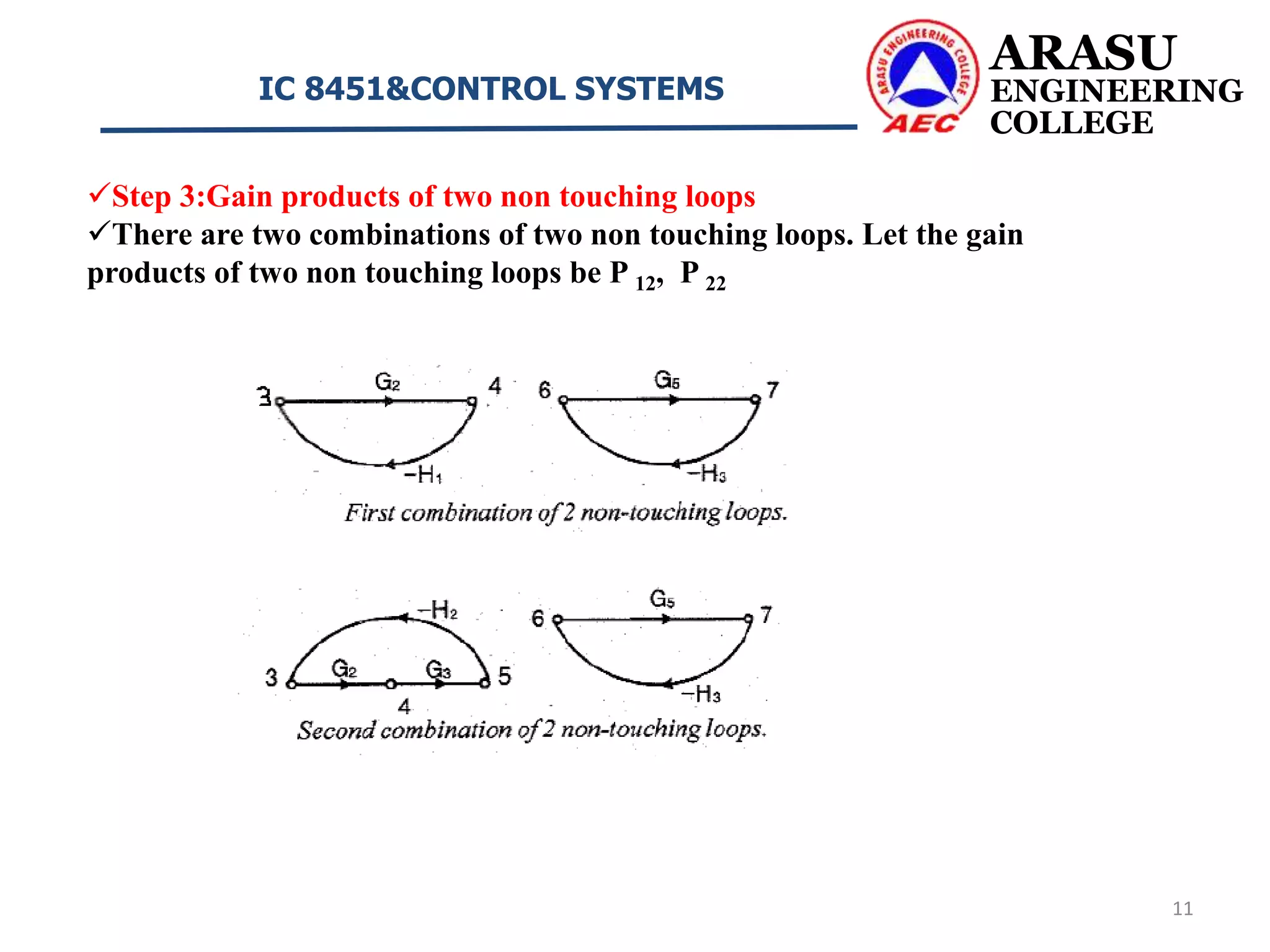
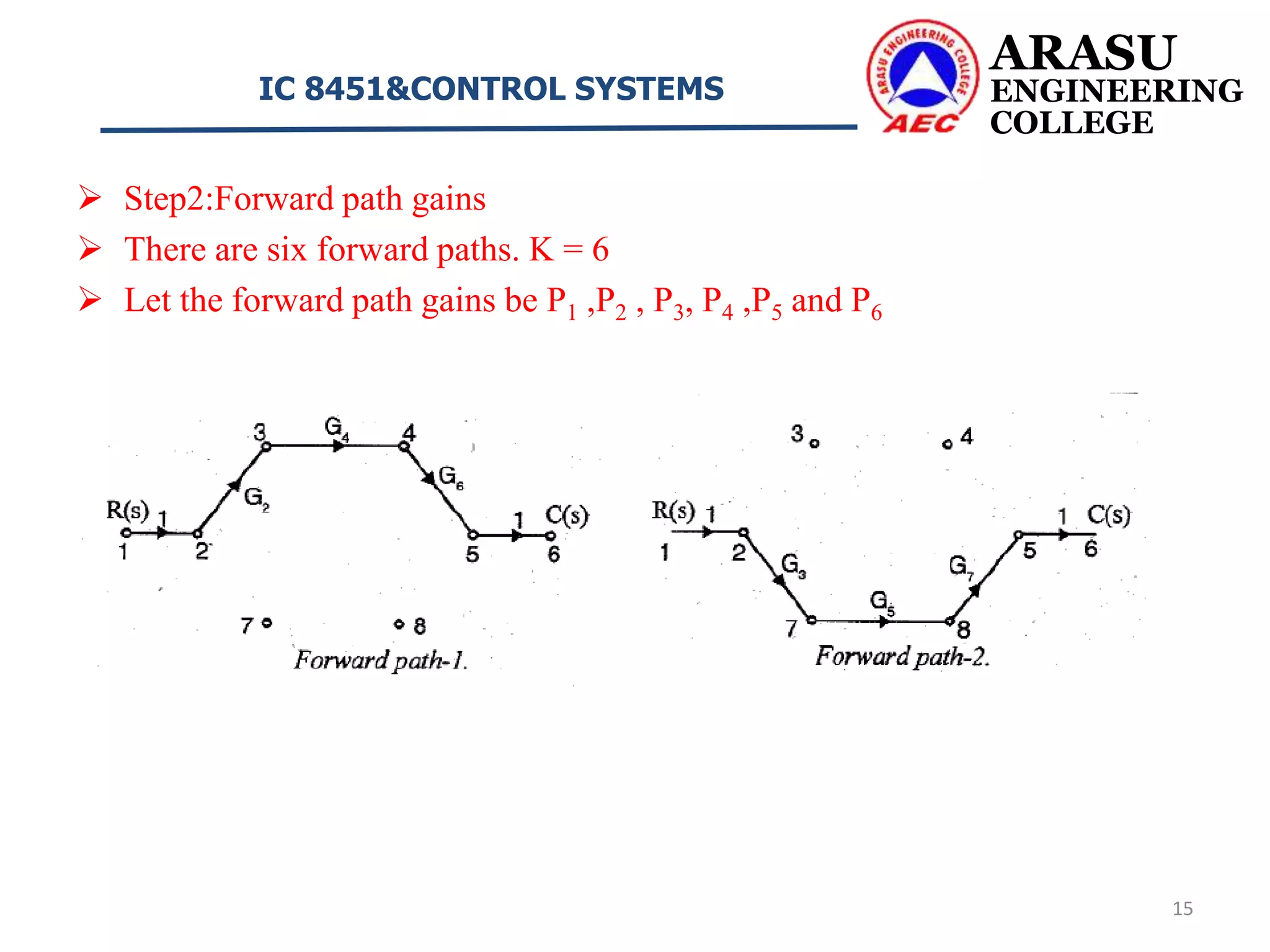
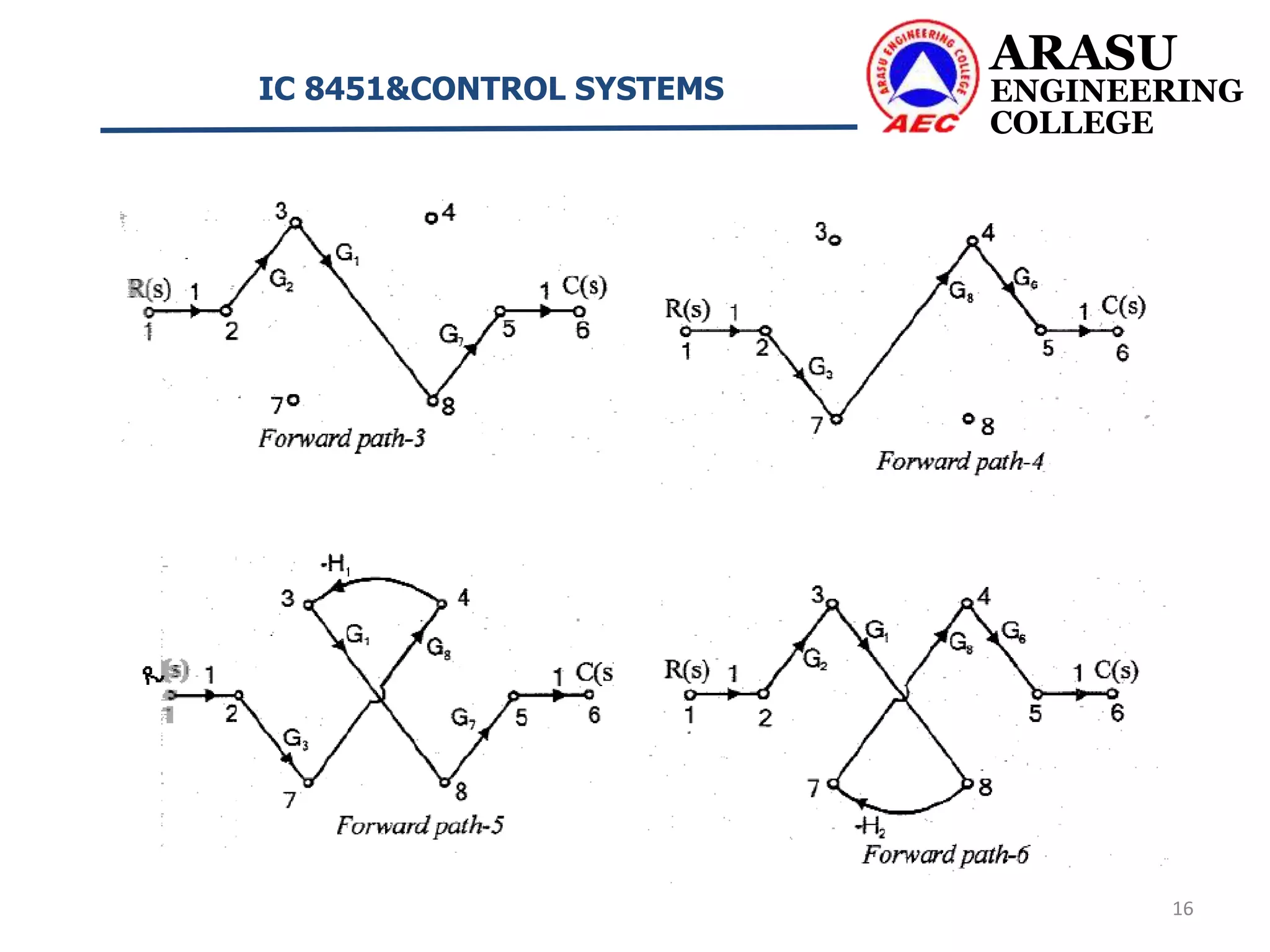
This document discusses signal flow graphs and Mason's gain formula for control systems. It begins by defining key terms used in signal flow graphs such as nodes, branches, transmittance, input/output nodes, paths, and loop gains. It then describes properties of signal flow graphs and how Mason's gain formula can be used to determine a system's transfer function from its signal flow graph. The document concludes by providing two example problems that demonstrate how to apply Mason's gain formula to calculate a system's overall transfer function.

1. IC 8451&CONTROL SYSTEMS
Department of Electrical and Electronics Engineering
Approved by AICTE | Affiliated to Anna University | Accredited by NAAC | Accredited NBA | Recognized by UGC under 2(f) and 12(B)
Chennai Main Road, Kumbakonam- 612 501.
ARASU ENGINEERING COLLEGE
1

2. ARASU
ENGINEERING
COLLEGE
IC 8451&CONTROL SYSTEMS
2
Prepared by
Mrs.K.KALPANA.,M.E.,(Ph.D.).,
Department of Electrical and Electronics Engineering

3. ARASU
ENGINEERING
COLLEGE
IC 8451&CONTROL SYSTEMS
3
 SIGNAL FLOW GRAPH
 The signal flow graph is used to represent the control system graphically and it was
developed b S.J. Mason.
 A signal flow graph is a diagram that represents a set of simultaneous linear algebraic
equations.
 By taking. Laplace transform, the time domain differential equations governing a
control system can be transferred to a set of algebraic equations in s-domain.
 The signal flow graph of the system can be constructed using these equations.
 Terms used in signal flow graph
 Node : A node is a point representing a variable or signal.
 Branch : A branch is directed line segment joining two nodes. The arrow on the
branch indicates the direction of signal flow and the gain of a branch is the
transmittance.
 Transmittance : The gain acquired by the signal when it travels from one node to
another is called transmittance. The transmittance can be real or complex.
 Input node (Source) : It is a node that has only outgoing branches.
 Output node (Sink) : It is a node that has only incoming branches.

4. ARASU
ENGINEERING
COLLEGE
IC 8451&CONTROL SYSTEMS
4
Mixed node : it is a node that has both incoming and outgoing branches.
Path : A path is a traversal of connected branches in the direction of the branch
arrows. The path should not cross a node more than once.
Open path : A open path starts at a node and ends at another node.
Closed path : Closed path starts and ends at same node.
Forward path : It is a path from an input node to an output node that does not cross any
node more than once.
Forward path gain : It is the product of the branch transmittances (gains) of a forward
path.
individual loop : It is a closed path starting from a node and after passing through a certain
part of a graph arrives at same node without crossing any node more than once.
Loop gain : It is the product of the branch transmittances (gains) of a loop.
Non-touching Loops : If the loops does not have a common node then they are said to be
non touching loops.

5.  PROPERTIES OF SIGNAL FLOW GRAPH
The basic properties of signal flow graph are the following:
 The algebraic equations which are used to construct signal flow graph must be in the
form of cause and effect relationship.
 Signal flow graph is applicable to linear systems only.
 A node in the signal flow graph represents the variable or signal.
 A node adds the signals of all incoming branches and transmits the sum to all outgoing
branches.
 A mixed node which has both incoming and outgoing signals can be treated as an
output node by adding an outgoing branch of unity transmittance.
 A branch indicates functional dependence of one signal on the other.
 The signals travel along branches only in the marked direction and when it travels it
gets multiplied by the gain or transmittance of the branch.
 The signal flow graph of system is not unique. By rearranging the system equations
different types of signal flow graphs can be drawn for a given system.
ARASU
ENGINEERING
COLLEGE
IC 8451&CONTROL SYSTEMS
5

6.  SIGNAL FLOW GRAPH REDUCTION
 MASON’S GAIN FORMULA
ARASU
ENGINEERING
COLLEGE
IC 8451&CONTROL SYSTEMS
6
The Mason’s gain formula is used to determine the transfer function of the
system from the signal flow graph of the system.
Let, R(s) = Input to the system
C(s) = Output of the system
Now, Transfer function of the system, T(s) =
Mason’s gain formula states the overall gain of the system [transfer function] as
follows,
Overall gain,

7. ARASU
ENGINEERING
COLLEGE
IC 8451&CONTROL SYSTEMS
7

8. ARASU
ENGINEERING
COLLEGE
IC 8451&CONTROL SYSTEMS
8
 EXAMPLE PROBLEM 1
 Find the overall transfer function of the system whose signal flow graph is
shown in fig
 Step 1: Forward path gain
 There are two forward paths . K = 2

9. ARASU
ENGINEERING
COLLEGE
IC 8451&CONTROL SYSTEMS
9
 Let forward path gains P1 and P2


10. ARASU
ENGINEERING
COLLEGE
IC 8451&CONTROL SYSTEMS
10
Step2:Individual loop gain
There are three individual loops. Let individual loop gains be P11, P21,
P31

11. ARASU
ENGINEERING
COLLEGE
IC 8451&CONTROL SYSTEMS
11
Step 3:Gain products of two non touching loops
There are two combinations of two non touching loops. Let the gain
products of two non touching loops be P 12, P 22

12. ARASU
ENGINEERING
COLLEGE
IC 8451&CONTROL SYSTEMS
12
Step 4: Calculation of ∆ and ∆k

13. ARASU
ENGINEERING
COLLEGE
IC 8451&CONTROL SYSTEMS
13
Step 5: Transfer function

14. ARASU
ENGINEERING
COLLEGE
IC 8451&CONTROL SYSTEMS
14
EXAMPLE PROBLEM 2
Find the overall gain of the system whose signal flow graph is shown in fig
Step 1 :Let us number the nodes

15.  Step2:Forward path gains
 There are six forward paths. K = 6
 Let the forward path gains be P1 ,P2 , P3, P4 ,P5 and P6
ARASU
ENGINEERING
COLLEGE
IC 8451&CONTROL SYSTEMS
15

16. ARASU
ENGINEERING
COLLEGE
IC 8451&CONTROL SYSTEMS
16

17. Forward path gains are
 Step3: Individual loop gain
There are three individual loops.
Let individual loop gains be P11 ,P21, P31
ARASU
ENGINEERING
COLLEGE
IC 8451&CONTROL SYSTEMS
17

18.  Step 4:Gain products of two non touching loops
 There is only one combination of two non touching loops .Let gain product of two non
touching loops be P 12 .
 Step 5: Calculation of ∆ and ∆k
ARASU
ENGINEERING
COLLEGE
IC 8451&CONTROL SYSTEMS
18

19.  The part of the graph which is non touching with forward path 1
 The part of the graph which is non touching with forward path 2
ARASU
ENGINEERING
COLLEGE
IC 8451&CONTROL SYSTEMS
19

20.  Step 6: Transfer function
ARASU
ENGINEERING
COLLEGE
IC 8451&CONTROL SYSTEMS
20