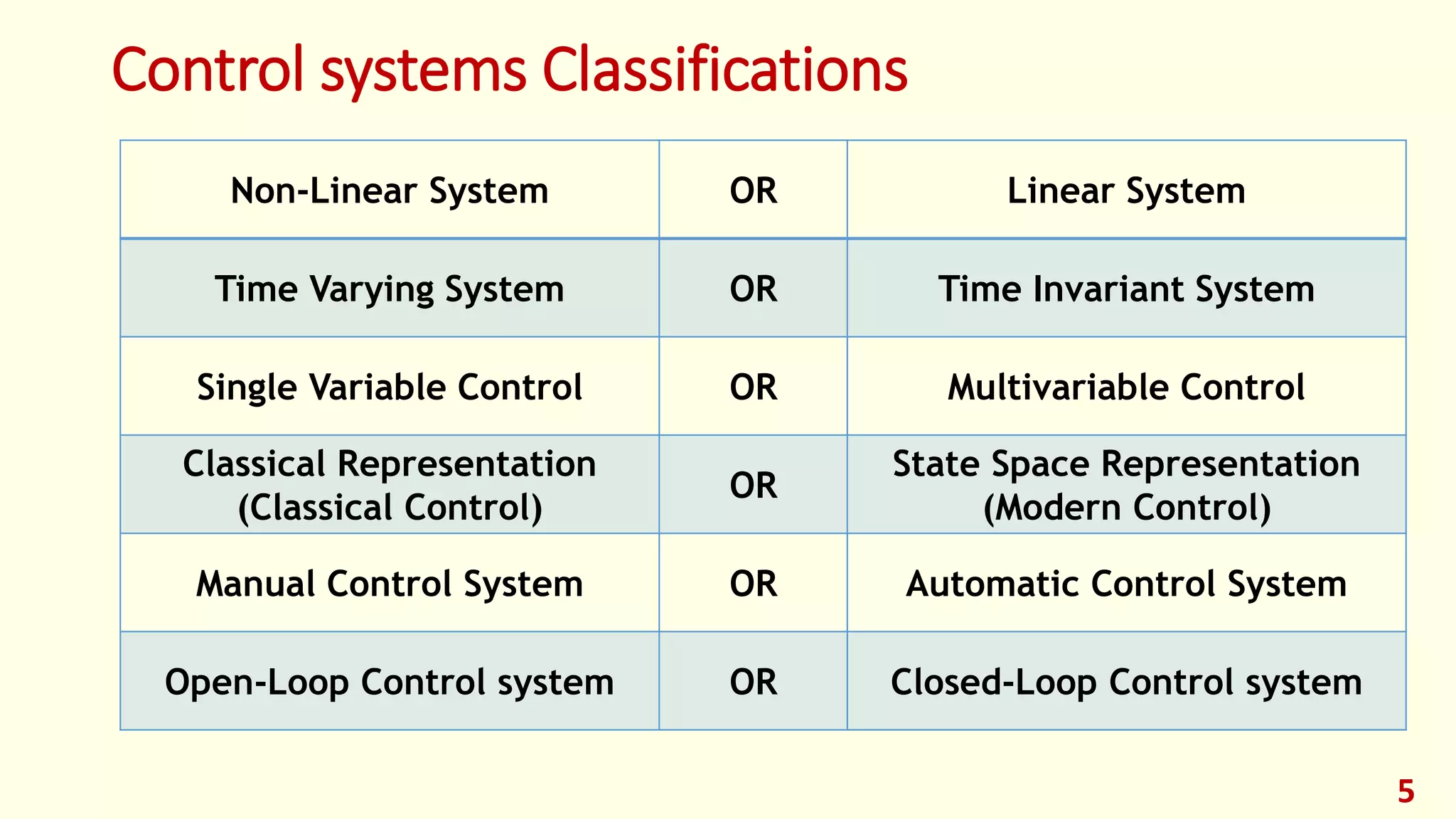
This document provides an overview of mathematical modeling of physical systems. It discusses how to derive mathematical models from physical systems using differential equations based on governing physical laws. The key steps are: (1) defining the physical system, (2) formulating the mathematical model using differential equations, and (3) solving the equations. Common model types include differential equation, transfer function, and state-space models. The document also discusses modeling various physical elements like electrical circuits, mechanical translational/rotational systems, and electro-mechanical systems using differential equations. It covers block diagram representation and reduction of mathematical models. The overall goal is to realize the importance of deriving accurate mathematical models for analyzing and designing control systems.

1. LECTURE (2)
Mathematical Modeling of
Systems
Assist. Prof. Amr E. Mohamed

2. Objectives
 In this lecture, we lead you through a study of mathematical models of
physical systems.
 After completing the chapter, you should be able to
 Describe a physical system in terms of differential equations.
 Understand the way these equations are obtained.
 Realize the use of physical laws governing a particular system such as
 Newton’s law for mechanical systems and Kirchhoff’s laws for electrical
systems.
 Realize that deriving mathematical models is the most important part of
the entire analysis of control systems.
2

3. Mathematical Model
 Mathematical modeling of any control system is the first and foremost task that a
control engineer has to accomplish for design and analysis of any control engineering
problem.
 A mathematical model of a dynamic system is defined as a set of differential equations
that represents the dynamics of the system accurately, or at least fairly well.
 Note that a mathematical model is not unique to a given system. A system may be
represented in many different ways and, therefore, may have many mathematical
models, depending on one’s perspective. For example,
 In optimal control problems, it is good to use state-space representations.
 On the other hand, for the transient-response or frequency-response analysis of single-
input-single-output, linear, time-invariant systems, the transfer function
representation may be more convenient than any other.
 Once a mathematical model of a system is obtained, various analytical and
computational techniques may be used for analysis and synthesis purposes. Because
the systems under consideration are dynamic in nature, the equations are usually
differential equations. If these equations can be linearized, then the Laplace
transform may be utilized to simplify the method of solution. 3

4. Different Mathematical Models
 Commonly used mathematical models are
 Differential equation model (Time Domain).
 Transfer function model (S-Domain).
 State space model (Time Domain).
 Use of the models depends on the application. For example, to find the
transient or steady state response of SISO (Single Input Single Output)
LTI (Linear Time Invariant) system transfer function model is useful. On
the other hand for optimal control application state space model is
useful.
4

5. Control systems Classifications
5
Non-Linear System OR Linear System
Time Varying System OR Time Invariant System
Single Variable Control OR Multivariable Control
Classical Representation
(Classical Control)
OR
State Space Representation
(Modern Control)
Manual Control System OR Automatic Control System
Open-Loop Control system OR Closed-Loop Control system

6. Laplace Transform
 Laplace Transforms: method for
solving differential equations,
converts differential equations
in time 𝑡 into algebraic
equations in complex variable 𝑠.
6

7. Laplace
Transform
Properties
7

8. The approach to dynamic system problems can be as follows:
1. Define the system and its components.
2. Formulate the mathematical model and list the necessary assumptions
3. Write the differential equations describing the model.
4. Solve the equations for the desired output variables.
5. Examine the solution and the assumptions.
6. If necessary reanalyze or redesign the system.
8

9. TRANSFER FUNCTION
 Transfer functions are commonly used to characterize the input—output
relationships of components or systems that can be described by linear,
time-invariant, differential equations.
 The transfer function of a linear, time-invariant, differential equation
system is defined as “the ratio of the Laplace transform of the output
(response function) to the Laplace transform of the input (driving
function) under the assumption that all initial conditions are zero”.

9

10. TRANSFER FUNCTION
 The general form of the differential equation for LTI-System is given by
𝒂 𝟎 𝒚
(𝒏)
+ 𝒂 𝟏 𝒚
(𝒏−𝟏)
+ … + 𝒂 𝒏−𝟏 𝒚 + 𝒂 𝒏 𝒚 = 𝒃 𝟎 𝒙
(𝒎)
+ 𝒃 𝟏 𝒙
(𝒎−𝟏)
+ … + 𝒃 𝒎−𝟏 𝒙 + 𝒃 𝒎 𝒙
 where y is the system output and x is the input of the System
 The transfer function of this system is obtained by taking the Laplace
transforms of both sides of Equation (under the assumption that all initial
conditions are zero),
𝑎0 𝑆 𝑛
𝑌 𝑠 + ⋯ + 𝑎 𝑛−1 𝑆1
𝑌 𝑠 + 𝑎 𝑛 𝑌 𝑠 = 𝑏0 𝑆 𝒎
𝑿(𝑠) + ⋯ + 𝑏 𝑚−1 𝑆 𝟏
𝑿(𝑠) + 𝑏 𝑚 𝑿(𝒔)
Then: 𝑎0 𝑆 𝑛
+ ⋯ + 𝑎 𝑛−1 𝑆1
+ 𝑎 𝑛 𝑌 𝑠 = 𝑏0 𝑆 𝒎
+ ⋯ + 𝑏 𝑚−1 𝑆 𝟏
+ 𝑏 𝑚 𝑿(𝒔)
10

11. TRANSFER FUNCTION
 Then the transfer function is
𝑻𝒓𝒂𝒏𝒔𝒇𝒆𝒓 𝑭𝒖𝒏𝒄𝒕𝒊𝒐𝒏 = 𝑮 𝒔 =
𝑳𝒂𝒑𝒍𝒂𝒄𝒆 𝒐𝒇 𝑶𝒖𝒕𝒑𝒖𝒕
𝑳𝒂𝒑𝒍𝒂𝒄𝒆 𝒐𝒇 𝑰𝒏𝒑𝒖𝒕 𝑨𝒔𝒔𝒖𝒎𝒊𝒏𝒈 𝒁𝒆𝒓𝒐 𝒊𝒏𝒊𝒕𝒊𝒂𝒍 𝑪𝒐𝒏𝒅𝒊𝒕𝒊𝒐𝒏
𝐺 𝑠 =
𝑌(𝑠)
𝑋(𝑠)
=
𝑏0 𝑆 𝒎 + ⋯ + 𝑏 𝑚−1 𝑆 𝟏 + 𝑏 𝑚
𝑎0 𝑆 𝑛 + 𝑎1 𝑆 𝑛−1 + ⋯ + 𝑎 𝑛−1 𝑆1 + 𝑎 𝑛
 Poles: are roots of the denominator (Values of s such that transfer
function becomes infinite)
 Zeros: are roots of the numerator (Values of s such that transfer
function becomes 0)
11

12. To derive the transfer function
1. Write the differential equation for the system.
2. Take the Laplace transform of the differential equation, assuming all
initial conditions are zero.
3. Take the ratio of the output Y(s) to the input R(s). This ratio is the
transfer function.
12

13. Describing Differential Equations for Electrical and
Electronic Elements
13

14. Electrical Circuits
14

15. Op Amps in system control
 Signal amplification in the sensor circuits
 Filters used for compensation purposes
 Modeling of the “real world” systems
 Lead or lag networks
 Design of controllers
15
u(s)
e(t) OPAMP+
-
OUT
R1
R2
u(t)
e(t)
OPAMP
+
-
OUT
R2
R1
Inverting amplifier Non-inverting amplifier
   te
R
R
tu
1
2
    te
R
R
tu 






1
2
1

16. Op Amps in system control
16
Summation circuit
        tetete
R
R
tu 321
1
2
OPAMP+
-
OUT
R1
R1
R1
R2
u(t)
e1(t)
e2(t)
e3(t)
U(s)
E(s) OPAMP+
-
OUT
Z1
Z2
 
  1
2
Z
Z
sE
sU

Transfer function of op amp

17. Op Amps in system control
17
U(s)
E(s)
C1
OPAMP+
-
OUT
R1
Integrator
 
  ITssCRZ
Z
sE
sU


11
111
2
Differentiator
 
  11
2
1
2


sCR
sCR
Z
Z
sE
sU

18. Op Amp lead-or-lag network
18
111
1
1


sCR
R
Z 122
2
2


sCR
R
Z
U(s)
E(s)
C2
OPAMP+
-
OUT
R1
R2
C1
 
  1
11
22
2
1
2 1
1 R
sCR
sCR
R
Z
Z
sE
sU 



19. Op Amp lead-lag network
19
 
  1
1
131
311
1



sCRR
RsCR
Z
 
  1
1
242
422
2



sCRR
RsCR
Z
Eo(s)
Ei(s)
C2
OPAMP+
-
OUT
R3
R4
C1
R1
R2
OPAMP+
-
OUT
R5
R6

20. Example: Write the integodifferential equations and the
transfer function of the following circuit
20
v(t))ii(
dt
d
LRi  2111
0
0
2
1
1222
 
t
dti
c
)ii(
dt
d
LRi
Take Laplace Transform of both
sides then find G(s) = I2(s)/V(s)

21. Describing Differential Equations for Translation
Mechanical Elements
21

22. Example: Write the differential equations and the transfer
function of the Spring Mass Damping System shown
22
s-domain
)()( sFsV
s
K
fMs v 






K
vf
M
)(tf
)(tv
)()(
)()(
2
2
tftKx
dt
tdx
f
dt
txd
M v 
differential equation
transfer function
 KsfMs
s
sF
sV
v 
 2
)(
)(

23. Example: Write the differential equations to model the
system shown
23
1K
1M
)(tf )(1 tx
2K
vf 2M
)(2 tx
3K
For the Mass M1
K2 (x1(t) – x2(t)) + K1x1(t) + fv d/dt (x1(t) – x2(t)) + M1 d2/dt2 x1(t) = f(t)
For the Mass M2
K2 (x1(t) – x2(t)) + fv d/dt (x1(t) – x2(t)) = K3x2(t) + M2 d2/dt2 x2(t)
Input
Output

24. Describing Differential Equations for Rotational
Mechanical Elements
24
Transfer Function for:
(a) Angular (b) Torque Displacement

25. Describing Differential Equations for Electro Mechanical
Elements
25
DC Motor
dt
td
Kv m
bb
)(
 Vb = Back electomotive force
Kb = the constant back emf
)()( sIKsT atm 
Tm = Torque of the motor
Kt = motor torque constant
)()()( 2
ssDsJsT mmmm 
Mechanical Relation
Electrical Relation








)(
1)(
)(
a
bt
m
m
mat
a
m
R
KK
D
J
ss
JRK
sE
s
Ia(s) = (Ea(s)-Vb(s))/(Ra+sLa)
The Transfer Function is

26. Block Diagram Models
 A block diagram of a system is a pictorial representation of the
functions performed by each component and of the flow of signals.
 Such diagram depicts the interrelationships that exist among the various
components. Differing from a purely abstract mathematical
representation, a block diagram has the advantage of indicating more
realistically the signal flows of the actual system.
 Transfer function can be represented as a block diagram:
26
)(sR )(sC
0
1
1
0
1
1
asasa
bsbsb
n
n
n
n
m
m
m
m









27. Components Of a block diagram for a LTI system
27

28. Procedures for drawing block diagram
1. Write the equations that describe the dynamic behavior for each
component.
2. Take Laplace transform of these equations, assuming zero initial
conditions.
3. Represent each Laplace-transformed equation individually in block
form.
4. Assembly the elements into a complete block diagram.
28

29. Example:
 Example derive the D.E. and the transfer function then draw the block
diagram for the following circuit:
 Take Laplace transform:
29
R
Cei eo
i
R
sEsE
R
tete
sI oioi )()()()(
)(







 
 L
C
idt
e
R
ee
i o
oi 


   
Cs
sI
C
idt
sEo 









L

30. Block Diagram Reduction
 Rules for reduction of the block diagram:
1. Any number of cascaded blocks can be reduced by a single block
representing transfer function being a product of transfer functions of
all cascaded blocks.
30

31. Block Diagram Reduction
2. Moving a summing point
31
(a) Behind the block
(b) Ahead of the block

32. Block Diagram Reduction
3. Moving a pickoff point
32
(a) Behind the block
(b) Ahead of the block

33. Block Diagram Reduction
4. Equivalent transfer function for parallel subsystems is the sum of
their transfer functions
33

34. Block Diagram Reduction
5. Feedback control system
34

35. Example reduce the following block diagram:
35
R
_+
_
+1G 2G 3G
1H
2H
+
+
C

36. Moving the summing point ahead of G1, we have:
36
R
_+
_
+ 1G 2G 3G
1H
1
2
G
H
+
+
C

37. Combing G1 and G2 in Cascade, we get:
37
R
_+
_
+ 21GG 3G
1H
1
2
G
H
+
+
C

38. Eliminating the feedback loop G1, G2 and H1 we get:
38
R
_+
_
+ 21GG 3G
1H
1
2
G
H
+
+
C

39. Combing the two blocks in Cascade, we get
39
R
_+
_
+
121
21
1 HGG
GG
 3G
1
2
G
H
C

40. Similarly eliminating the second feedback loop we get:
40
R
_+
_
+
121
321
1 HGG
GGG

1
2
G
H
C

41. Similarly eliminating the third feedback loop we get:
41
R
_+
232121
321
1 HGGHGG
GGG

C

42. The system is reduced to the following block diagram:
42
R
321232121
321
1 GGGHGGHGG
GGG

C

43. Conclusions of block diagram reduction Technique
1. Numerator of the closed-loop transfer function C(s)/R(s) is the product
of the transfer functions of the feedforward path.
2. The denominator of the closed-loop transfer function C(s)/R(s) is equal
to:
1 − Σ( 𝑝𝑟𝑜𝑑𝑢𝑐𝑡 𝑜𝑓 𝑡ℎ𝑒 𝑡𝑟𝑎𝑛𝑠𝑓𝑒𝑟 𝑓𝑢𝑛𝑐𝑡𝑖𝑜𝑛𝑠 𝑎𝑟𝑜𝑢𝑛𝑑 𝑒𝑎𝑐ℎ 𝑙𝑜𝑜𝑝)
3. The positive feedback loop yields a negative term in the denominator.
43

44. Example of system with two inputs R(s) and D(s)
1. Find 𝑌1(𝑠)/𝐷(𝑠) when 𝑅(𝑠) = 0
2. Find 𝑌2(𝑠)/𝑅(𝑠) when 𝐷(𝑠) = 0
3. Deduce the total response 𝑌(𝑠) of the
control system when R(s) and D(s) ≠ 0
𝑌1 𝑠
𝐷 𝑠 𝑅 𝑠 =0
=
𝐺2
1 + 𝐺2(𝐻1 − 𝐻2)
𝑌2 𝑠
𝑅 𝑠 𝐷 𝑠 =0
=
𝐺1 𝐺2
1 + 𝐺2(𝐻1 − 𝐻2)
𝑌 𝑠 = 𝑌1 𝑠 + 𝑌2 𝑠 =
𝑌1 𝑠
𝐷 𝑠 𝑅 𝑠 =0
. 𝐷(𝑠) +
𝑌2 𝑠
𝑅 𝑠 𝐷 𝑠 =0
. 𝑅(𝑠)
𝑌 𝑠 =
𝐺2
1 + 𝐺2 𝐻1 − 𝐻2
𝐷 𝑠 +
𝐺1 𝐺2
1 + 𝐺2 𝐻1 − 𝐻2
𝑅(𝑠)
44

45. Signal Flow Graph Models
 Definitions:
45
input node (source)
b1x a
2x
c
4x
d
1
3x
3x
output node (sink)
mixed node
input node (source)
mixed node
forward path
path
loop
branch
node
transmittance

46. Signal Flow Graph Models
 Node: a point representing a signal or variable.
 Branch: unidirectional line segment joining two nodes.
 Path: a branch or a continuous sequence of branches that can be
traversed from one node to another node.
 Loop: a closed path that originates and terminates on the same node
and along the path no node is met twice.
 Nontouching loops: two loops are said to be nontouching if they do not
have a common node.
46

47. Flow graphs of control systems
47
)(sR
)(sG
)(sC
)(sG)(sR )(sC
block diagram signal flow graph
)(sR
_+
)(sH
)(sG
)(sC)(sE
)(sG
)(sR
)(sC
1
)(sE )(sH

48. Mason’s Signal Flow Graph Gain Formula
 The transfer function T(s) of a closed loop control system is:
 Where
∆ = 1 – Σ(All different loop gains)
+ Σ(Gain products of all combinations of two non-touching loops)
- Σ(Gain products of all combinations of three non-touching loops)
+ …
 Pk : The paths connecting the input R(s) and the output Y(s)
 ∆k : is ∆ with the loops touching the kth path removed
48



k kpk
sR
sY
sT
)(
)(
)(

49. Example:
1. Calculate forward path transfer function Pk for each forward path k.
2. Calculate all loop TF’s.
3. Consider nontouching loops 2 at a time.
 Loops L1 do not touch Loops L3 and L4
 Loops L2 do not touch Loops L3 and L4
49
87652
43211
GGGGP
GGGGP


774663
332221
,
,,
HGLHGL
GHLHGL



50. Example:
5. Calculate Δ.
6. Calculate Δk for each forward path.
7. The TF of the system is
50
   4232413143211 LLLLLLLLLLLL 
 
 212
431
1
1
LL
LL


   
   423241314321
2187654343212211
1
11
)(
)(
)(
LLLLLLLLLLLL
LLGGGGLLGGGGPP
sT
sR
sY







51. Block Diagram to Signal Flow Graph
 The SFG can be constructed from the block diagram as show in the
following example:
 To get the transfer function, we use the Mason’s Gain Formula. 51

52. 52