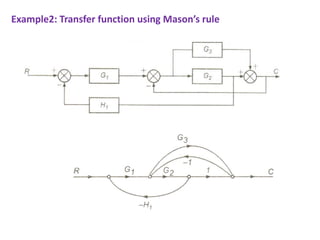
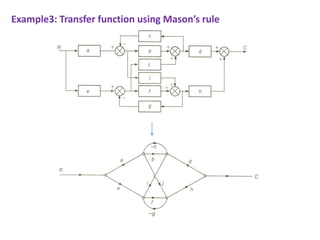
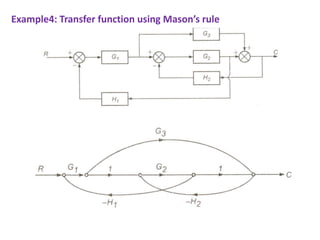
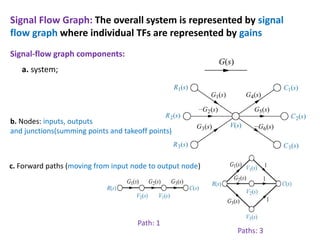
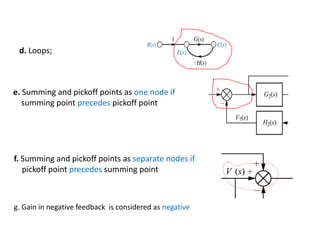
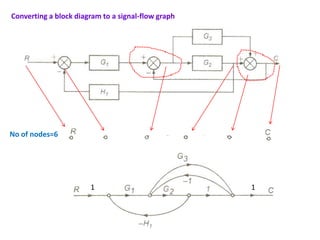
The document discusses signal flow graphs and Mason's rule for determining transfer functions from signal flow graphs. Mason's rule states that the transfer function is equal to the sum of the products of the forward path gains and the cofactors of the individual loops, divided by the overall cofactor. Several examples are provided to demonstrate applying Mason's rule to calculate transfer functions from given signal flow graphs.

1. CONTROL SYSTEMS
(L11)

2. Signal Flow Graph: The overall system is represented by signal
flow graph where individual TFs are represented by gains
a. system;
Signal-flow graph components:
b. Nodes: inputs, outputs
and junctions(summing points and takeoff points)
c. Forward paths (moving from input node to output node)
Path: 1
Paths: 3

3. e. Summing and pickoff points as one node if
summing point precedes pickoff point
f. Summing and pickoff points as separate nodes if
pickoff point precedes summing point
d. Loops;
g. Gain in negative feedback is considered as negative

4. Converting a block diagram to a signal-flow graph
No of nodes=7
Summing
point
Summing
and take off
points
take off
point
Summing
point
take off
point output
input

5. Converting a block diagram to a signal-flow graph
1 1
No of nodes=6

6. TF by Mason’s Rule: The Transfer function. C(s)/ R(s), of a system
represented by a signal-flow graph is
𝑇 𝑠 =
𝐶(𝑠)
𝑅(𝑠)
=
σ𝑘 𝑃𝑘∆𝑘
∆
=
𝑃1∆1 + 𝑃2∆2 + 𝑃3∆3 … . .
∆
K = number of forward paths
Pk = the kth forward-path gain
∆ = 1 - individual loop gains + gain of 2 non touching loops - gain of 3 non
touching loops + gain of 4 non touching loops - …….
∆𝑘= ∆ not touching the kth forward path

7. Example1: Transfer function using Mason’s rule
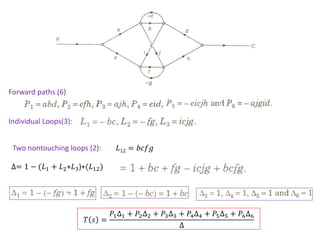
Forward path (1) : P1 = G1(s)G2(s)G3(s)G4(s)G5(s)
Loops(4): L1= G2(s)H1(s), L2=G4(s)H2(s), L3=G7(s)H4(s), L4=G2(s)G3(s)G4(s)G5(s)G6(s)G7(s)G8(s)
Two nontouching loops(3): L12= G2(s)H1(s)G4(s)H2(s), L13=G2(s)H1(s)G7(s)H4(s), L23=G4(s)H2(s)G7(s)H4(s)
Three nontouching loops(1): L123=G2(s)H1(s)G4(s)H2(s)G7(s)H4(s)
= 1-[G2(s)H1(s)+G4(s)H2(s)+G7(s)H4(s)+ G2(s)G3(s)G4(s)G5(s)G6(s)G7(s)G8(s)] + [G2(s)H1(s)G4(s)H2(s)
+ G2(s)H1(s)G7(s)H4(s) + G4(s)H2(s)G7(s)H4(s)] – [G2(s)H1(s)G4(s)H2(s)G7(s)H4(s)]
∆= 1 − (𝐿1 + 𝐿2+𝐿3+𝐿4)+(𝐿12+𝐿13 + 𝐿23) − 𝐿123
∆𝑘= ∆1= 1 − 𝐿3 = 1 − 𝐺7(𝑠)𝐻4(𝑠) 𝑇 𝑠 =
𝑃1∆1
∆

8. Example2: Transfer function using Mason’s rule

9. Forward paths(2):
Individual loops(3):
𝑇 𝑠 =
𝑃1∆1 + 𝑃2∆2
∆
=
𝐺1𝐺2 + 𝐺1𝐺3
1 + 𝐺2 + 𝐺3 + 𝐺1𝐺2𝐻1

10. Example3: Transfer function using Mason’s rule

11. Forward paths (6)
Individual Loops(3):
Two nontouching loops (2): 𝐿12 = 𝑏𝑐𝑓𝑔
∆= 1 − (𝐿1 + 𝐿2+𝐿3)+(𝐿12)
𝑇 𝑠 =
𝑃1∆1 + 𝑃2∆2 + 𝑃3∆3 + 𝑃4∆4 + 𝑃5∆5 + 𝑃6∆6
∆

12. Example4: Transfer function using Mason’s rule

13. Forward paths (2):
Individual Loops(3):
𝑇 𝑠 =
𝑃1∆1 + 𝑃2∆2
∆
=
𝐺1𝐺2 + 𝐺1𝐺3
1 + 𝐺2𝐻2 + 𝐺1𝐺2𝐻1 − 𝐺1𝐺2𝐺3𝐻1𝐻2