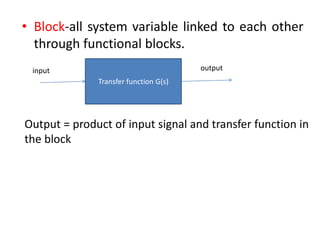
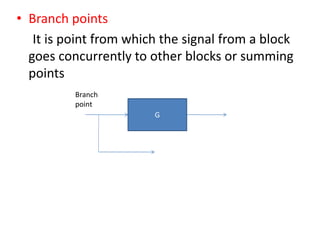
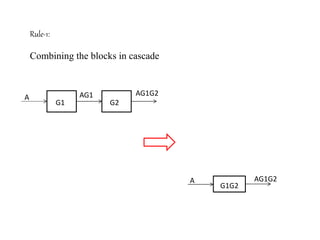
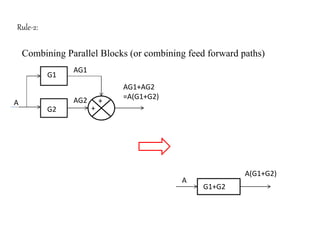
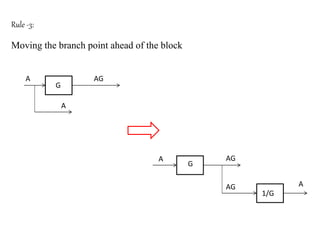
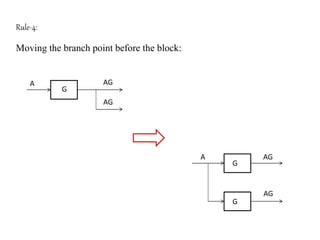
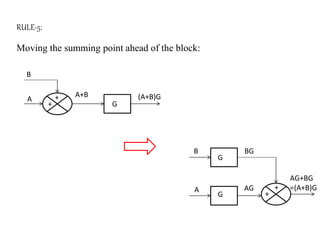
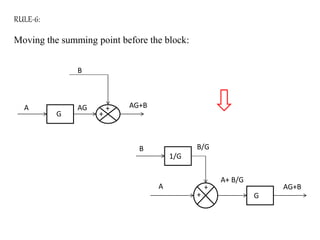
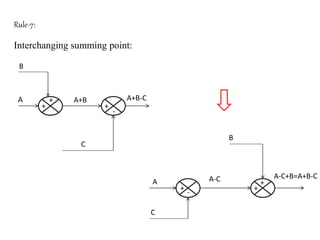
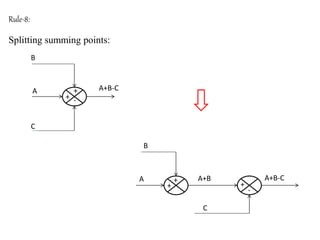
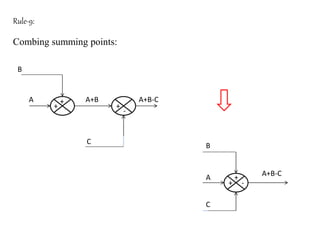
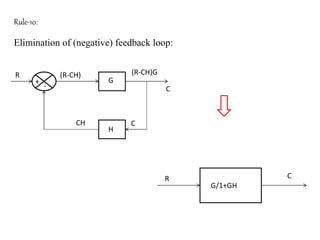
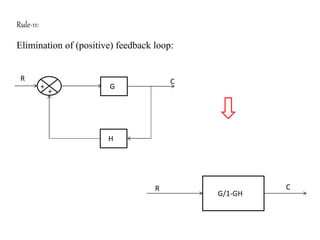
The document provides a comprehensive overview of block diagrams and signal flow graphs used in control engineering, detailing their components and reduction rules. It discusses how to construct and analyze these diagrams to find transfer functions, including Mason's gain formula and various pathways for signal flow. Additionally, it outlines procedures for converting block diagrams into signal flow graphs, emphasizing the importance of proper node representation and gain marking.

1. BLOCK DIAGRAM
• A block diagram is a pictorial representation of
the functions performed by each component
and of the flow of signals.
Elements of a block diagram
Block
Branch point
Summing point

2. • Block-all system variable linked to each other
through functional blocks.
Transfer function G(s)
input output
Output = product of input signal and transfer function in
the block

3. • Summing point-add two or more signals in the
system
a
b
a-b

4. • Branch points
It is point from which the signal from a block
goes concurrently to other blocks or summing
points
G
Branch
point

5. BLOCK DIAGRAM REDUCTION

6. Rule-1:
Combining the blocks in cascade
G1 G2
A AG1 AG1G2
G1G2
A AG1G2

7. Rule-2:
Combining Parallel Blocks (or combining feed forward paths)
A
G1
G2 +
+
AG1+AG2
=A(G1+G2)
AG2
G1+G2
A(G1+G2)
A
AG1

8. Rule -3:
Moving the branch point ahead of the block
A
G
AG
AG
1/G
A
G
AG
A
A

9. Rule-4:
Moving the branch point before the block:
A
G
AG
AG
A
G
G
AG
AG

10. RULE-5:
Moving the summing point ahead of the block:
`
A
B
A+B
+
+
G
(A+B)G
B
A
G
G
BG
AG
+
+
AG+BG
=(A+B)G

11. RULE-6:
Moving the summing point before the block:
`
`
`
B
A AG
+
+
G
AG+B
B
1/G
B/G
A+ B/G
A
G
AG+B
+
+

12. Rule-7:
Interchanging summing point:
A
B
+
+ A+B
+
-
A+B-C
C
A
B
C
+ -
A-C +
+
A-C+B=A+B-C

13. Rule-8:
Splitting summing points:
+
+
-
+
+
+
-
A
B
C
A+B-C
A
B
A+B A+B-C
C

14. Rule-9:
Combing summing points:
B
B
A
C
A+B-C
+
+
-
+
+
A A+B A+B-C
+
-
C

15. Rule-10:
Elimination of (negative) feedback loop:
+
-
G
H
C
(R-CH)G
(R-CH)
R
CH
C
G/1+GH
R C

16. Rule-11:
Elimination of (positive) feedback loop:
+
+
R
G
H
C
G/1-GH
R C

17. CONTROL ENGINEERING
PROBLEM
BLOCK DIAGRAM REDUCTION

18. Reduce the block diagram shown in figure and find C/R.

19. STEP 1: MOVE THE BRANCH POINT AFTER THE BLOCK

20. STEP 2: ELIMINATE THE FEEDBACK PATH AND COMBINING
BLOCKS IN CASCADE

21. STEP 3: COMBINING PARALLEL BLOCKS

22. STEP 4: COMBINING BLOCKS IN CASCADE

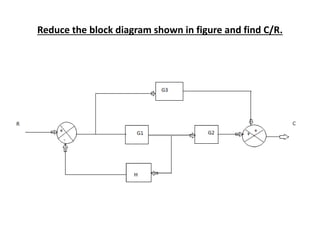
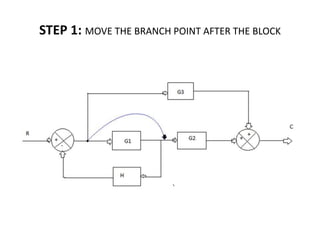
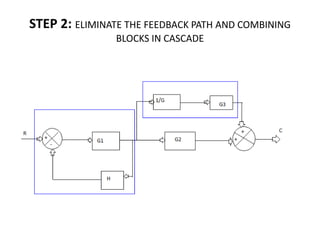
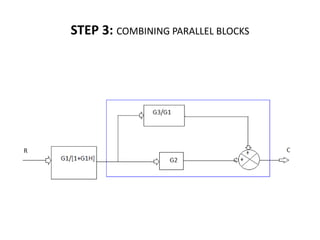
23. (C/R)=[G1/(1+G1H)][G2+(G3/G1)]
=[G1/(1+G1H)][(G1G2+G3)/G1]
=[(G1G2+G3)/(1+G1H)]

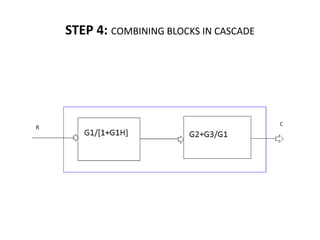
24. RESULT
THE OVER ALL TRANSFER FUNCTION OF THE SYSTEM,
(C/R)=[(G1G2+G3)/(1+G1H)]

25. • Simplify the block diagram and find the
transfer function of the given system.

26. • Step 1 - Use Rule 1 for blocks G1 and G2. Use
Rule 2 for blocks G3 and G4.
• Step 2 - Use Rule 3 for blocks G1G2 and H1. Use
Rule 4 for shifting take-off point after the
block G5.
• Step 3 - Use Rule 1 for blocks (G3+G4)and G5.
• Step 4 - Use Rule 3 for blocks (G3+G4)G5 and H3.
• Step 5 − Use Rule 1 for blocks connected in
series.
• Step 6 − Use Rule 3 for blocks connected in
feedback loop.

28. SIGNAL FLOW GRAPH
Signal flow graph is used to represent the control
system graphically
It represents a set of simultaneous linear algebraic
equations. By taking laplace transform, the time
domain differential equations governing a control
system can be transferred to a set of algebraic
equations in s domain.
The signal flow graph of the system can be
constructed using this equation
NODE: is a point representing a variable or signal

29. SIGNAL FLOW GRAPH
 BRANCH: is a directed line segment joining two nodes.
The arrow on the branch indicates the direction of signal
flow and gain of a branch is the transmittance.
 TRANSMITTANCE: gain acquired by the signal when it
travels from one node to another is called transmittance.
It can be real or complex.
 INPUT NODE OR SOURCE: it is a node having only
outgoing branches
 OUTPUT NODE OR SINK: It is a node that has only
incoming branches
 MIXED NODE: both incoming and outgoing branches.

30. SIGNAL FLOW GRAPH
PATH: Is a traversal of connected branches in the
direction of the arrows. The path should not cross a
node more than once.
OPEN PATH: starts at a node and ends at another
node.
CLOSED PATH: starts and ends at same node.
FORWARD PATH: it is a path from an input node to
an output node that does not cross any node more
than once.
FORWARD PATH GAIN: it is the product of the
branch transmittance(gains) of a forward path.
INDIVIDUAL LOOP: it is a closed path starting from a
node and after passing through a certain part of a
graph arrives at the same node without crossing
any node more than once.

31. SIGNAL FLOW GRAPH
 LOOP GAIN: is a product of the branch transmittance
(gains) of the loop.
 NON TOUCHING LOOPS: if the loop does not have a
common mode then they are said to be non touching
loops.

32. SIGNAL FLOW GRAPH REDUCTION
S.J.Manson has developed a simple
procedure to determine the transfer
function of the system represented as a
signal flow graph

33. TRANSFER FUNCTION
Transfer function of the system
T(s)=C(s)/R(s)
where,
R(s)=input to the system
C(s)=output of the system

34. Manson’s gain formula
 Overall gain T=1/
T=T(s)=transfer function of the system
Pk = forward path gain of the kth forward path
Δ = 1-(sum of individual loop)+(sum of gain products of all
possible combinations of two non touching loops)-
(sum of gain products of all possible combinations of
three non touching loops)+….
Δk = Δ for that part of the graph which is not touching kth
forward path

35. PROBLEM
Find the overall transfer function of the
system whose figure is shown
2
1 8
4
3 7
6
5
1
-H1
G6
-H3
-H2
1
G1
G2 G3 G4 G5

36. 1.forward path gain=> there are 2 forward path k=2
let forward path gain be p1 and p2
 Gain of forward path 1, P1=G1G2G3G4G5
 Gain of forward path 2, P2=G4G5G6
1 2 3 4 5 6 7 8
1
1
G5
G1 G4
G3
G2
1 2 3 4 5 6 7 8
G6
G5
G4 1
1

37. 2.Individual loop gain
There are three individual loop. Let loop gains
beP11 ,P21 and P31
P11= -G2H1
P21= -G2G3H2
P31= -G5H3
3 3
4 4 5
6 7
-H1
-H2
-H3
G5
G3
G2
G2

38. 3.Gain products of two non touching loops
There are two combinations of two non-
touching loops. Let the gain products of two
non touching loops be P12 and P22
3 4
-H1 -H3
6 7
3 4 5
-H2 6 7
G2
G2
G3
G5
G5
-H3

39. Gain product of first combination of two non
touching loops
P12 = P11P31=(-G2H1)(-G5H3)
= G2G5H1H3
Gain product of second combination of two non
touching loop
P22 = P21P31 =(-G2G3H2)(-G5H3)
= G2G3G5H2H3

40. Calculation of Δ and Δk
Δ=1-(P11 + P21 + P31)+(P12 + P22 )
=1-(-G2H1-G2G3H2-G5H3)+
(G2G5H1H3+G2G3G5H2H3)
=1+G2H1+G2G3H2+G5H3+G2G5H1H3+G2G3G5H2H3
Δ1 = 1 there is no part of graph which is not
touching with first forward path

41. • The part of the graph which is non touching
with second forward path is shown in fig
• Δ2=1-P11=1-(-G2H1)=1+G2H1
3 4
G2
-H1

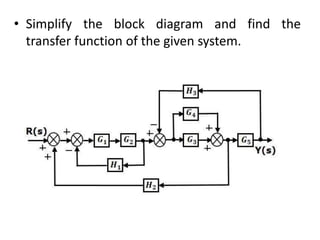
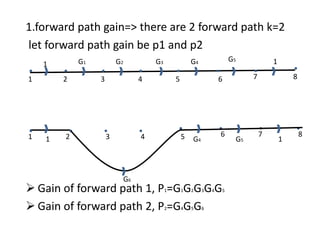
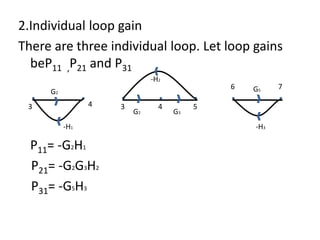
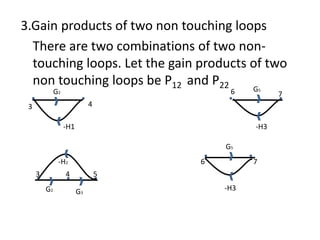
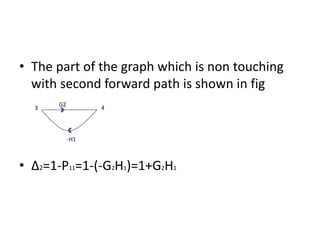
42. Transfer function, T
by Mason’s gain formula the TF,
T=1/Δ
= 1/Δ(P1Δ1+P2Δ2) (K=2, we have 2
forward paths)
T=[G1G2G3G4G5+G4G5G6(1+G2H1)]/
[1+G2H1+G2G3H2+G5H3+G2G5H1H3+G2
G3G5H2H3]

43. PROCEDURE FOR CONVERTING BLOCK
DIAGRAM TO SIGNAL FLOW GRAPH
 Assume nodes at i/p, o/p, at every summing point, at
every branch point and in between cascaded blocks
 Draw the nodes separately as small circles and number
the circles in the order 1,2,3,…..etc
 From the block diagram find the gain between each node
in the main forward path and connect all the
corresponding circles by straight line and mark the gain
between the nodes
 Draw the feed forward path between various nodes and
mark the gain of feed forward path along with sign
 Draw the feedback paths between various nodes and
mark the gain of feedback paths along with sign