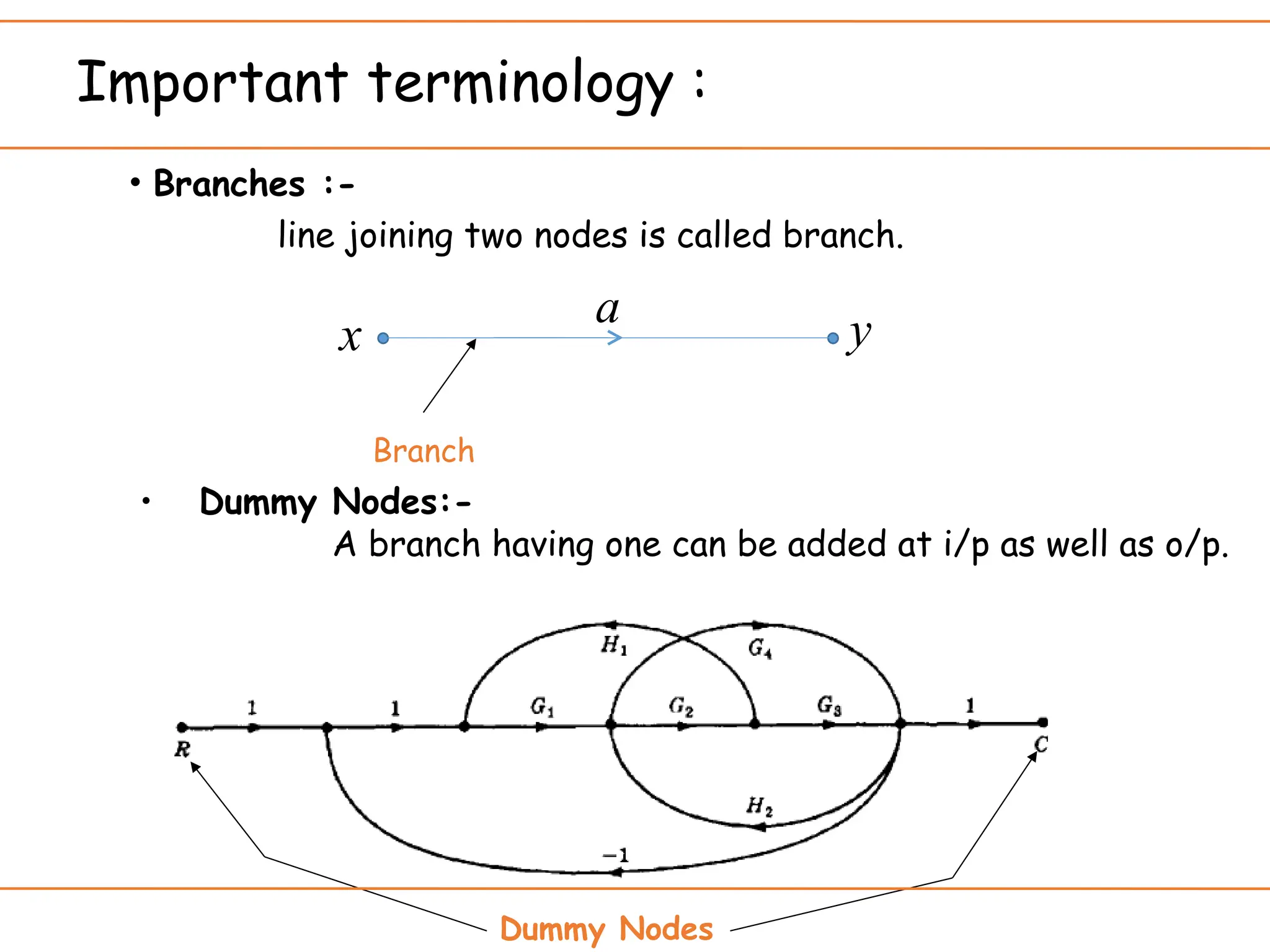
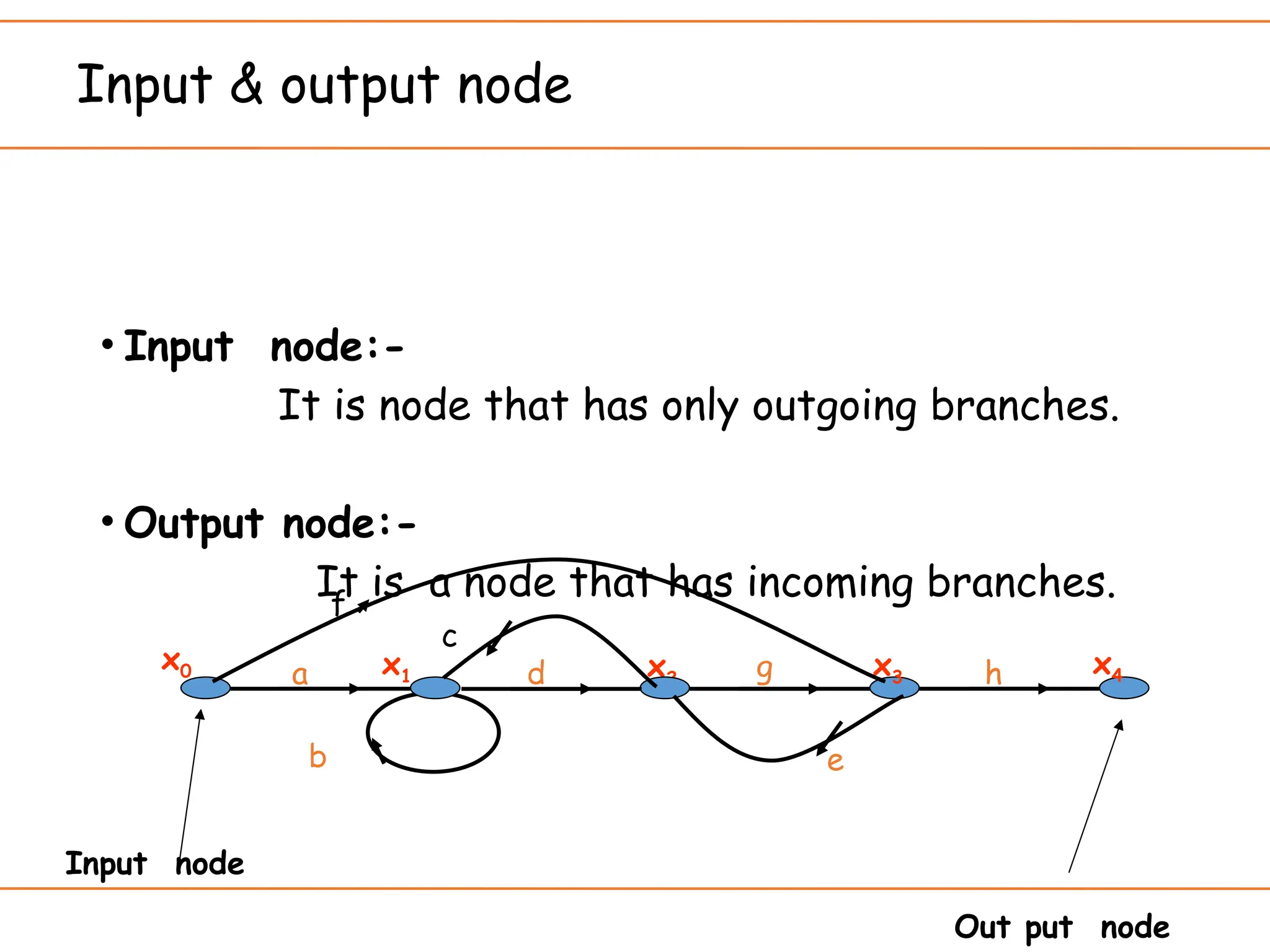
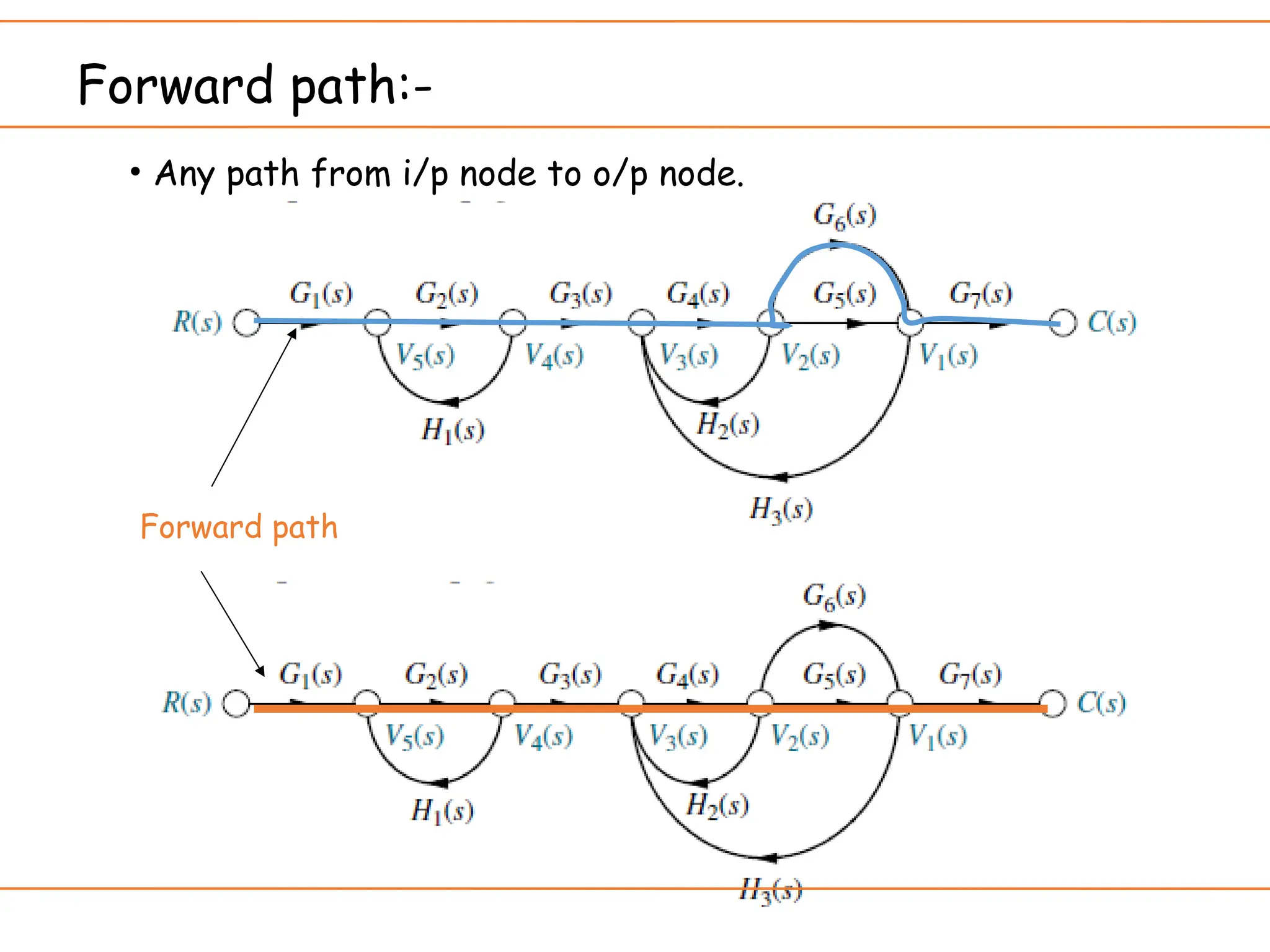
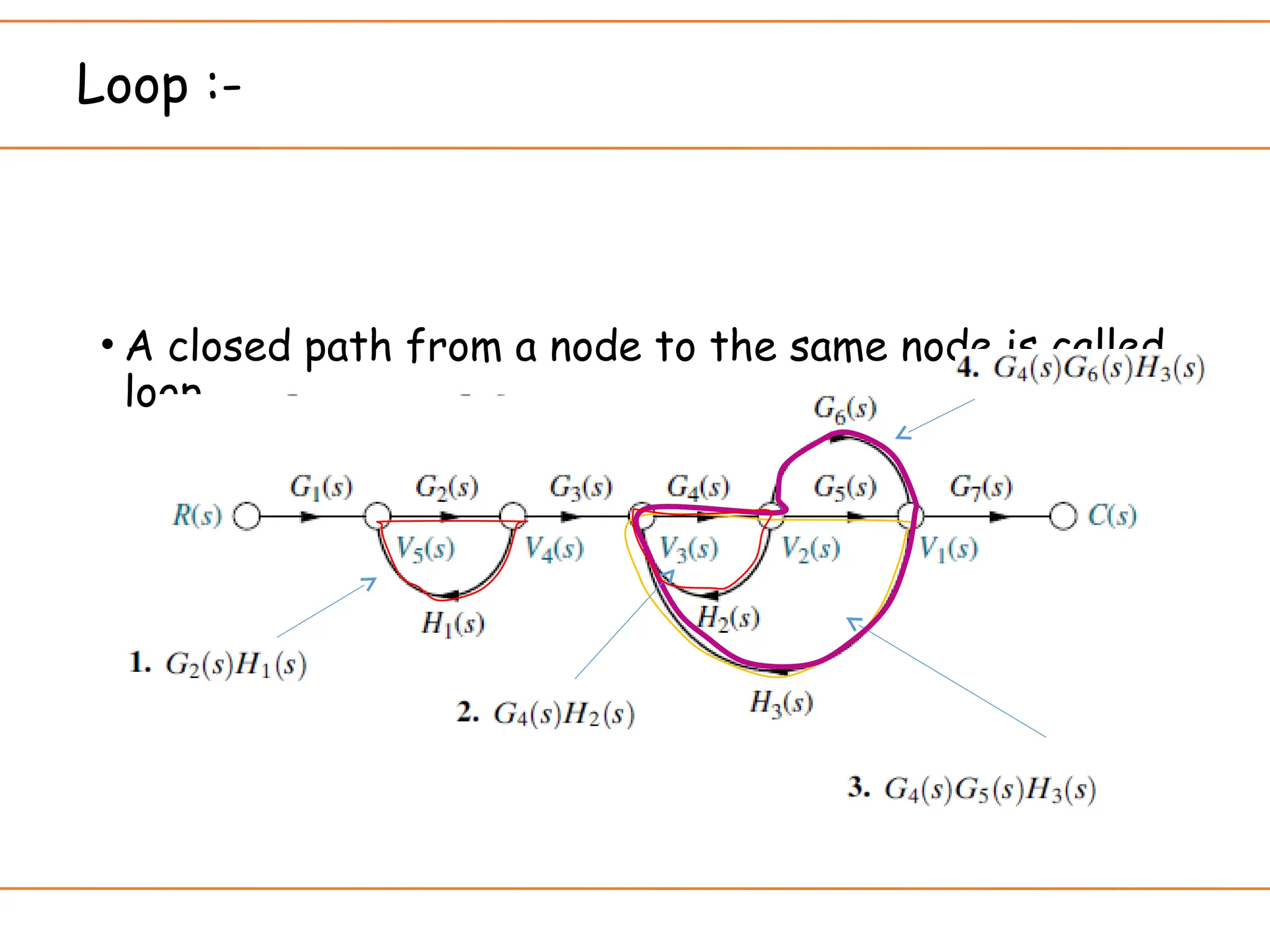
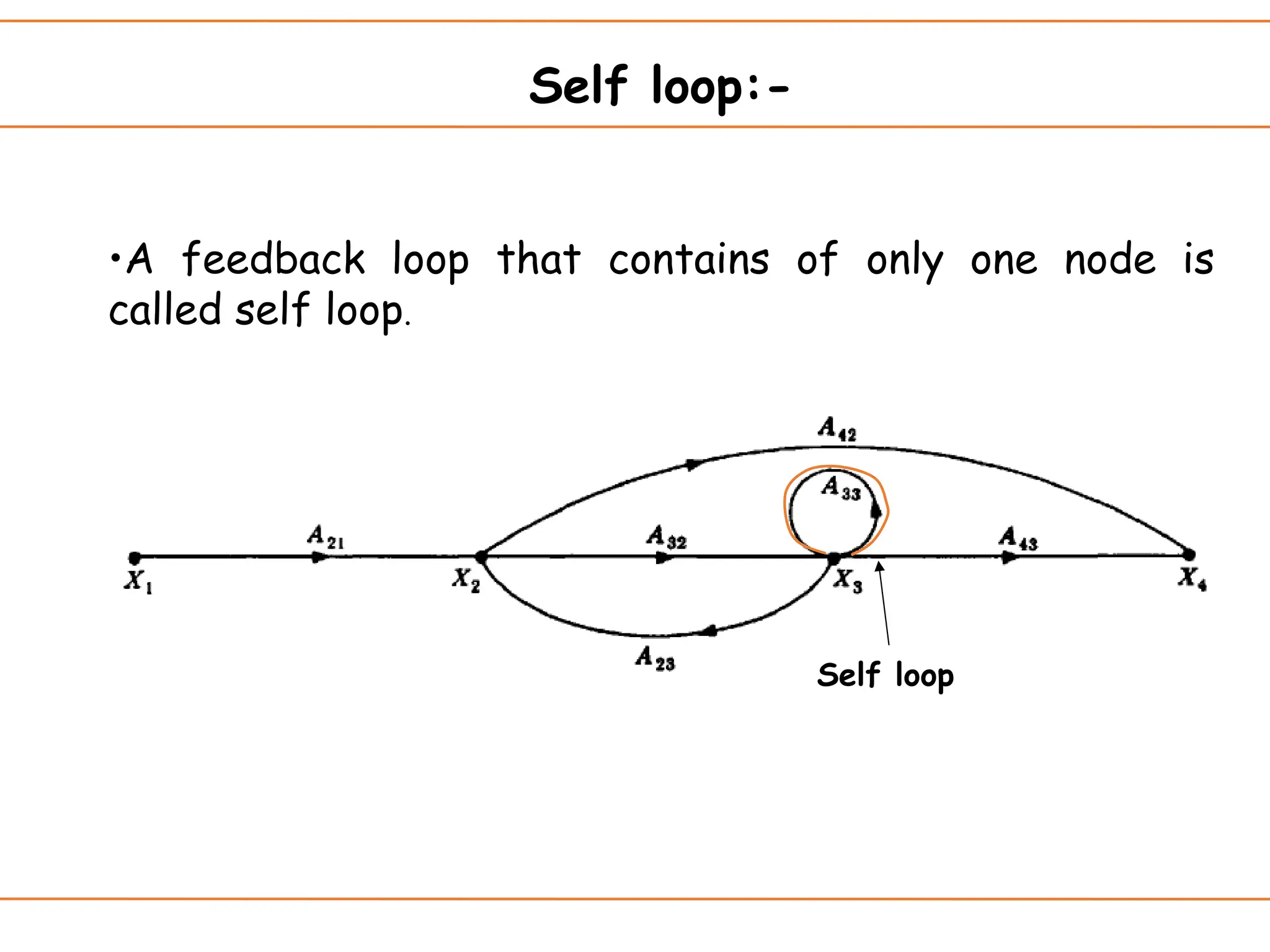
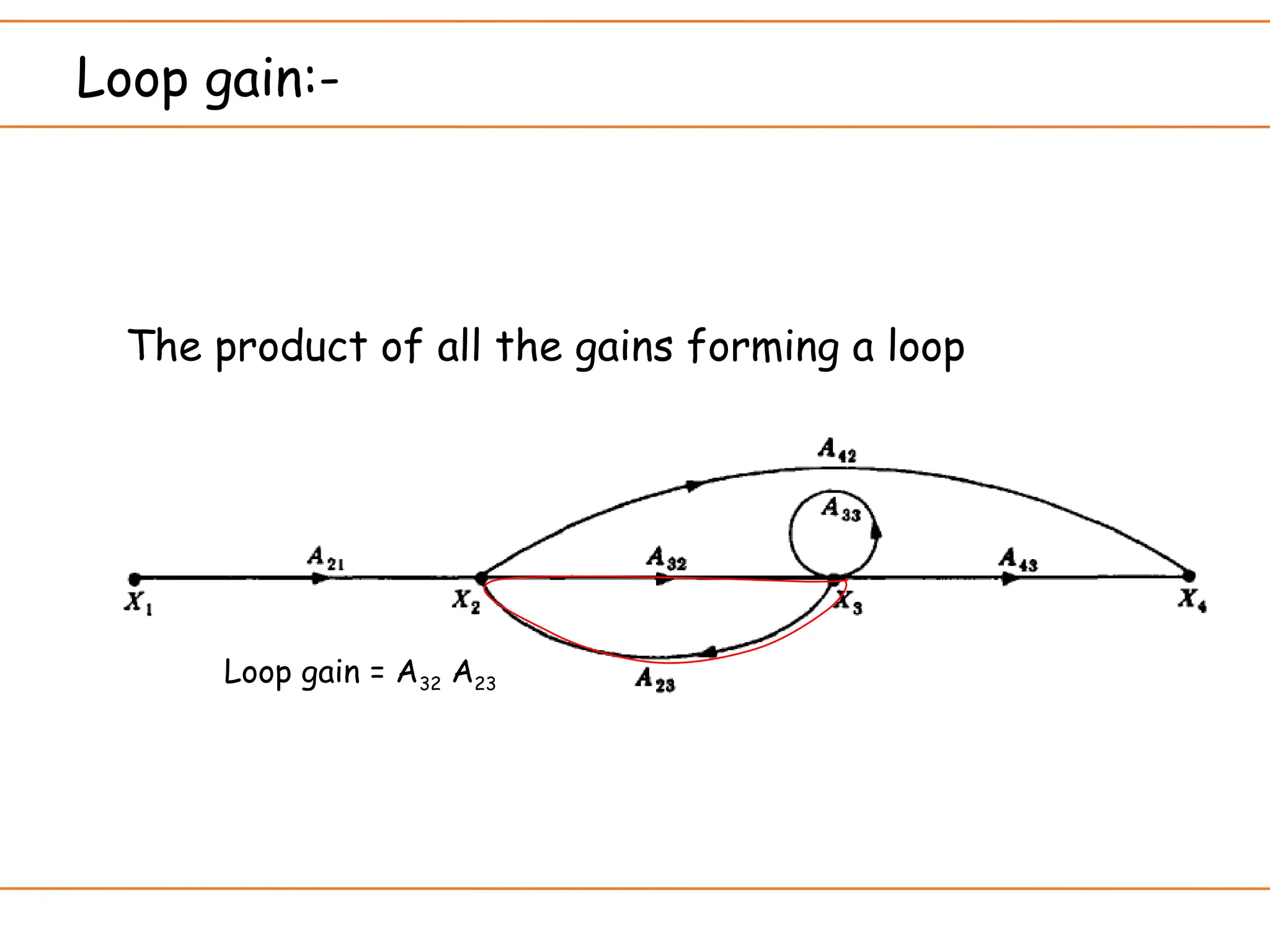
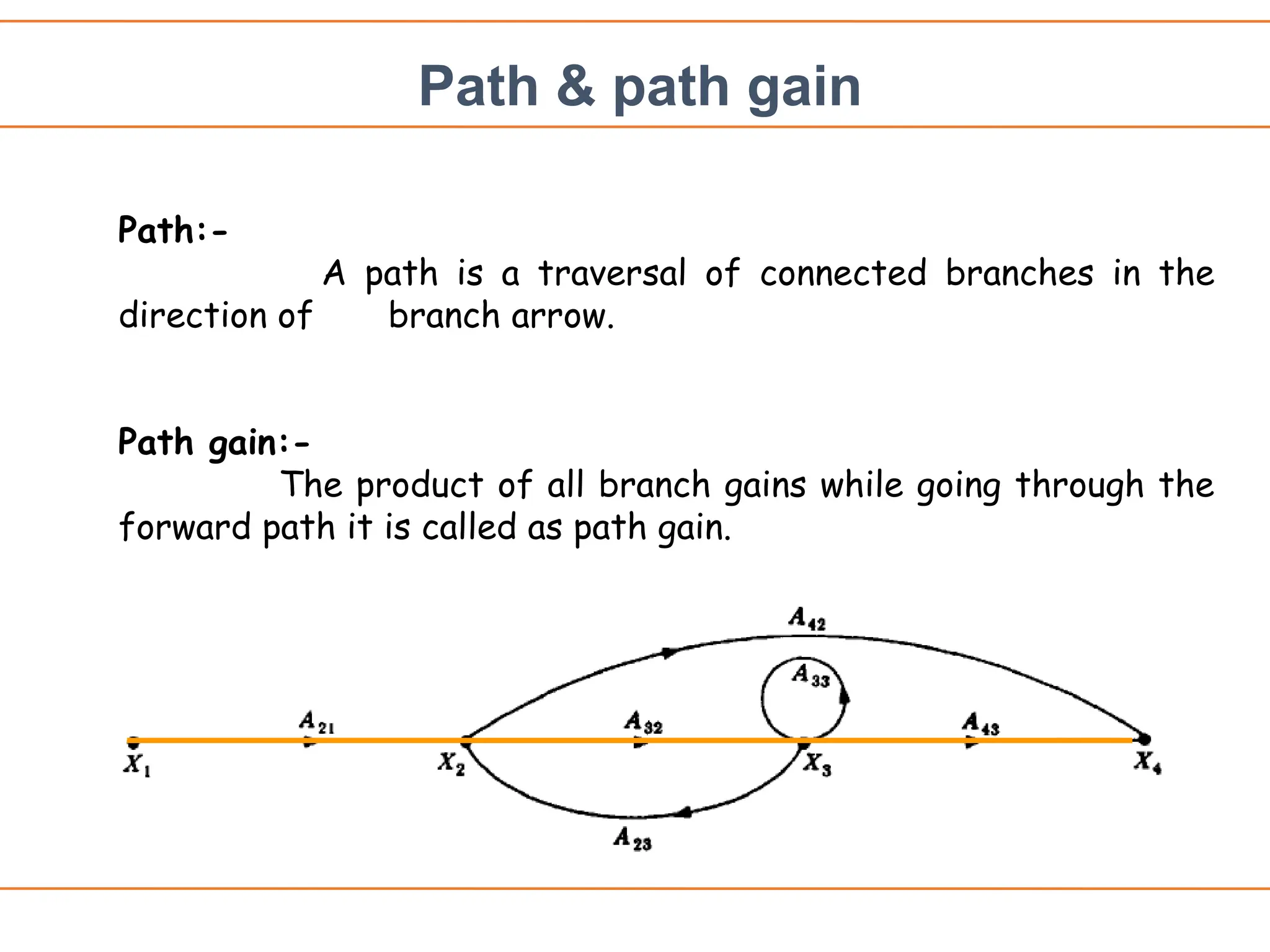
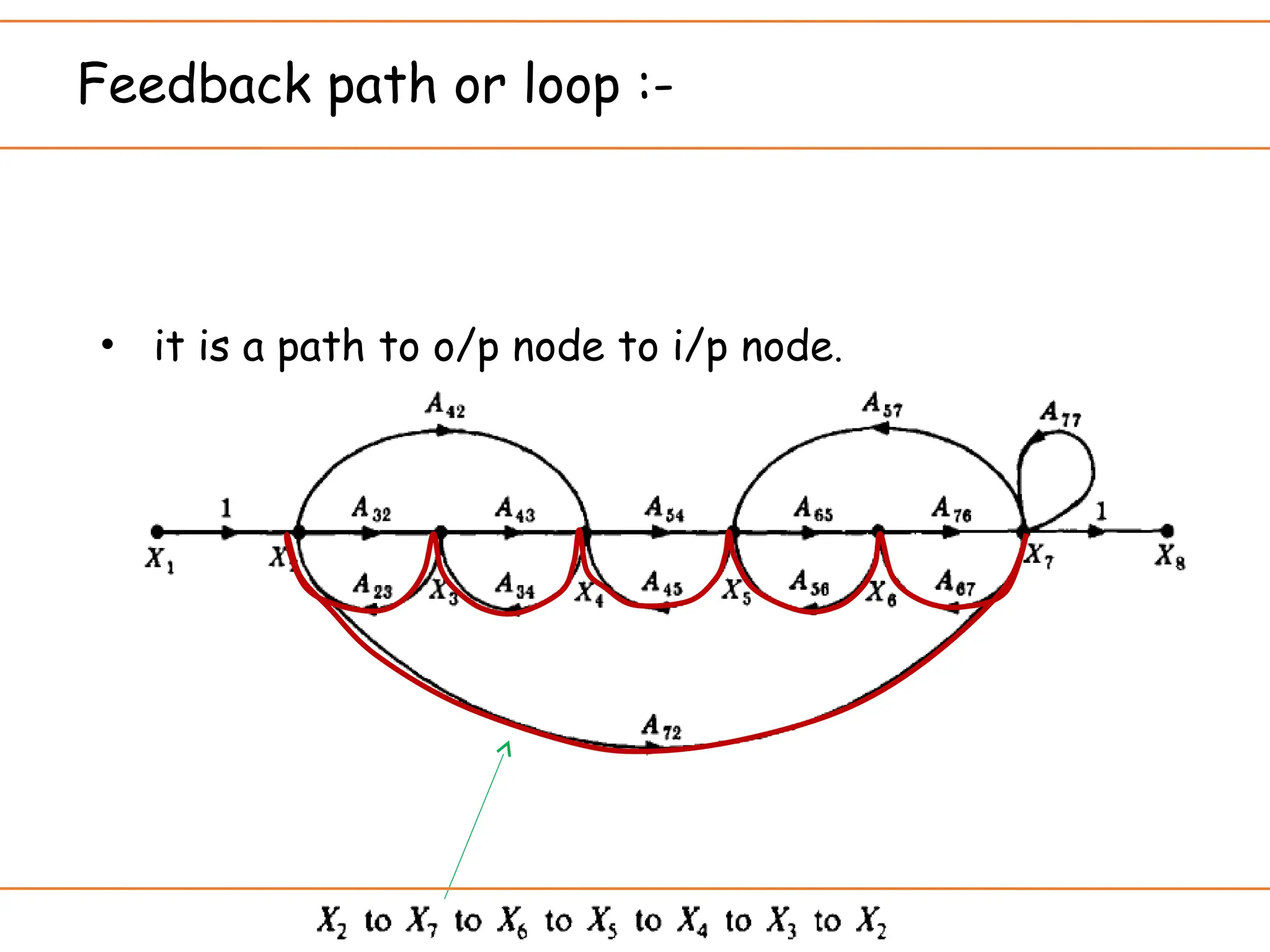
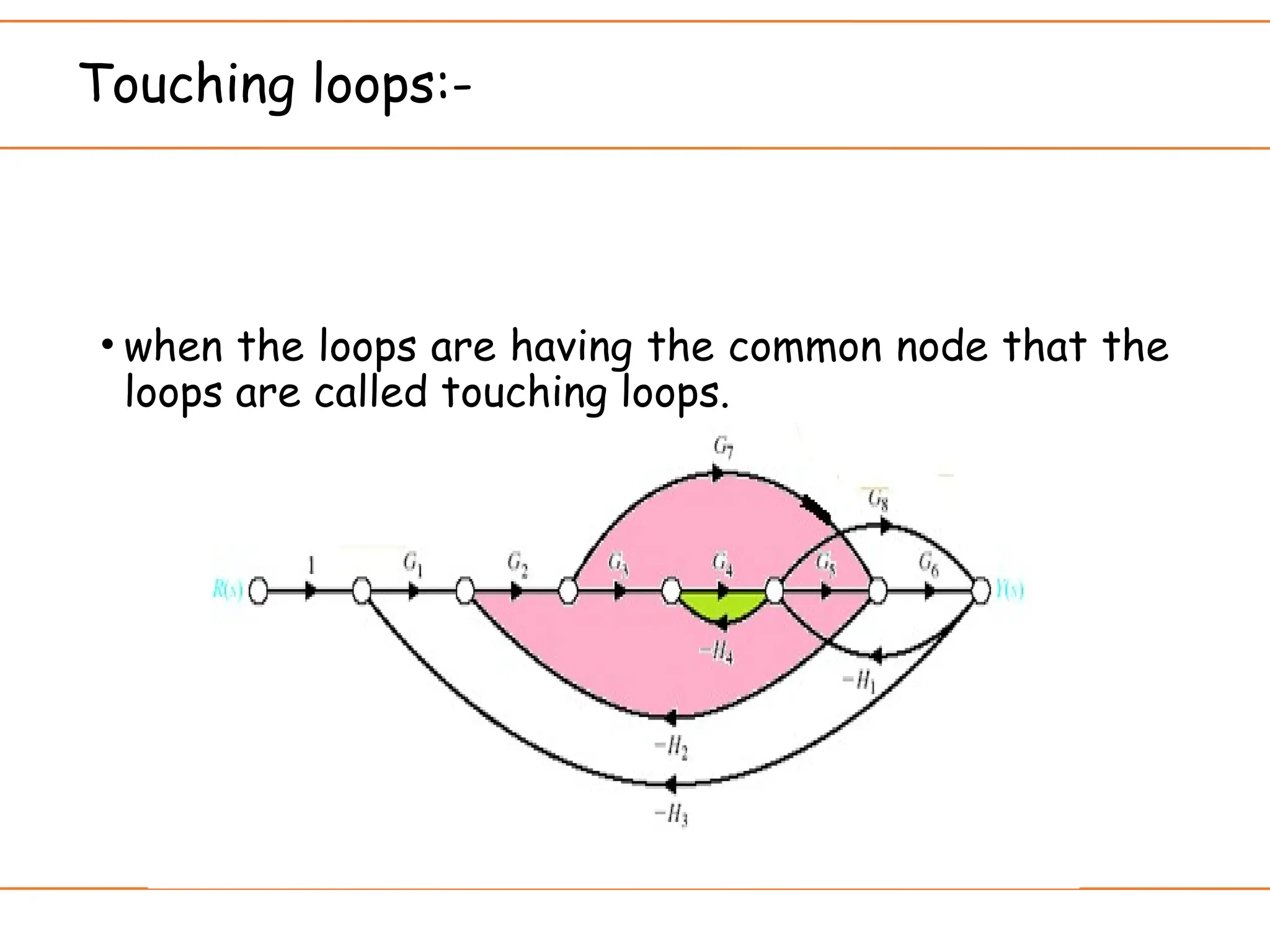
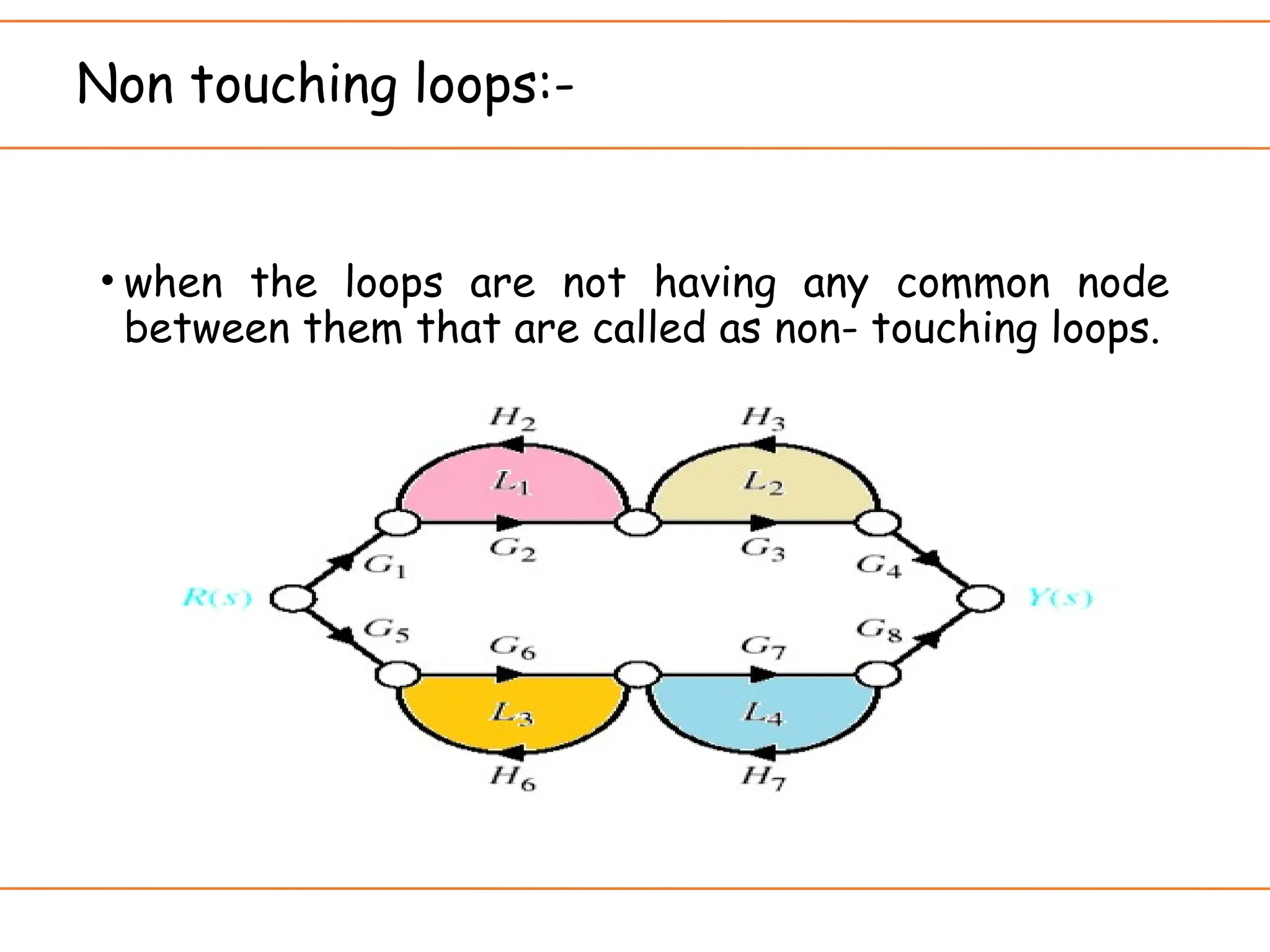
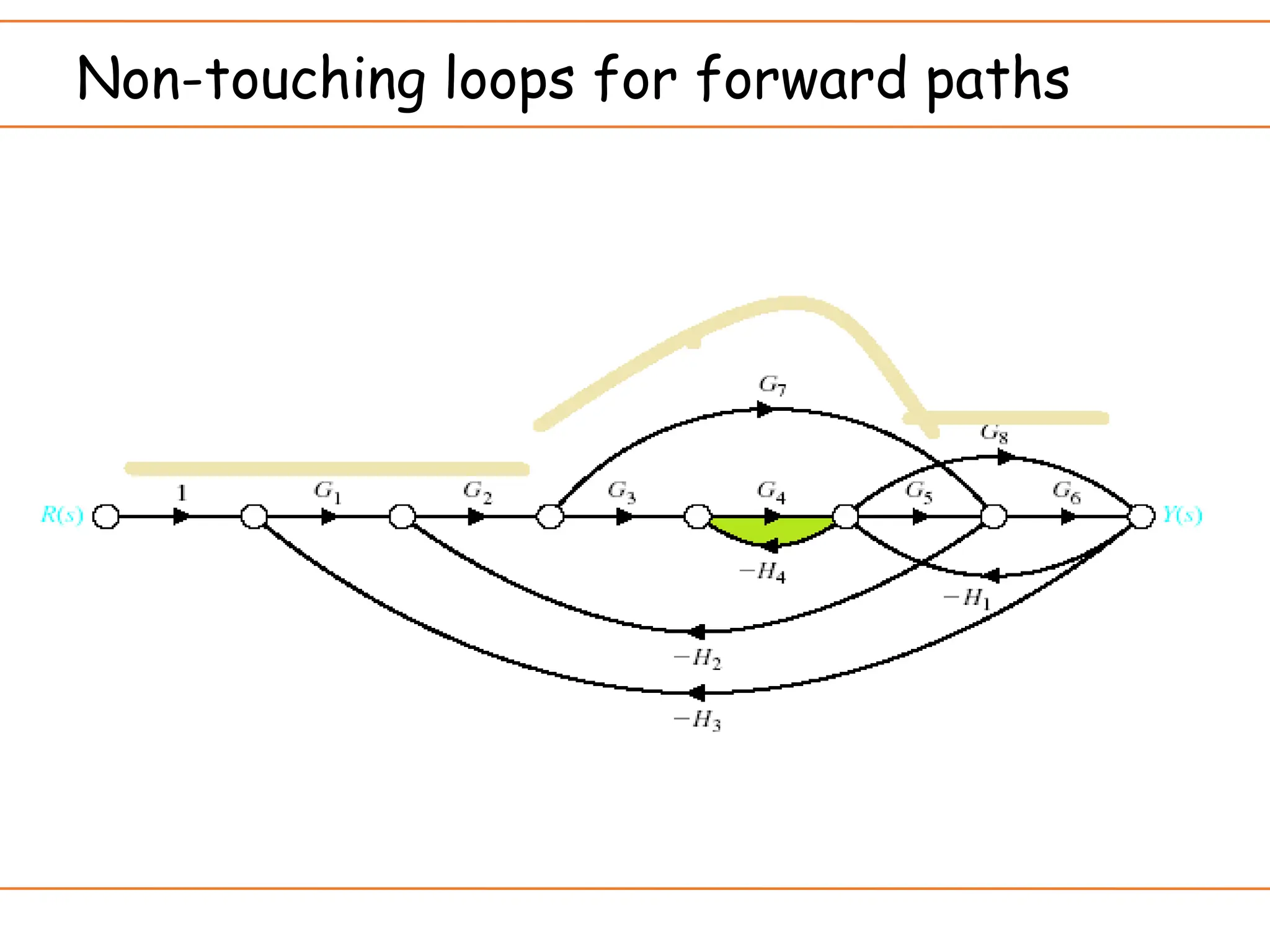
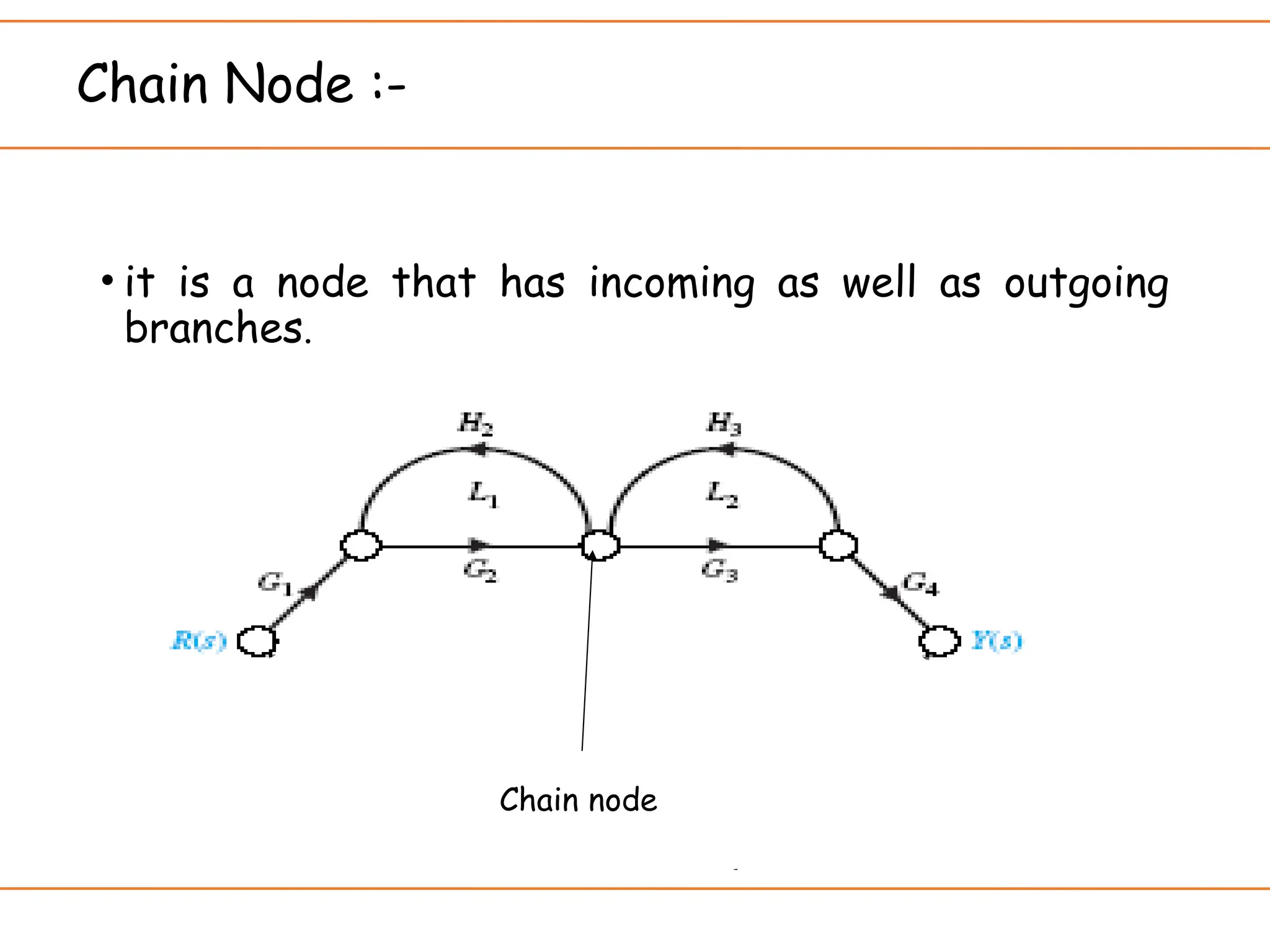
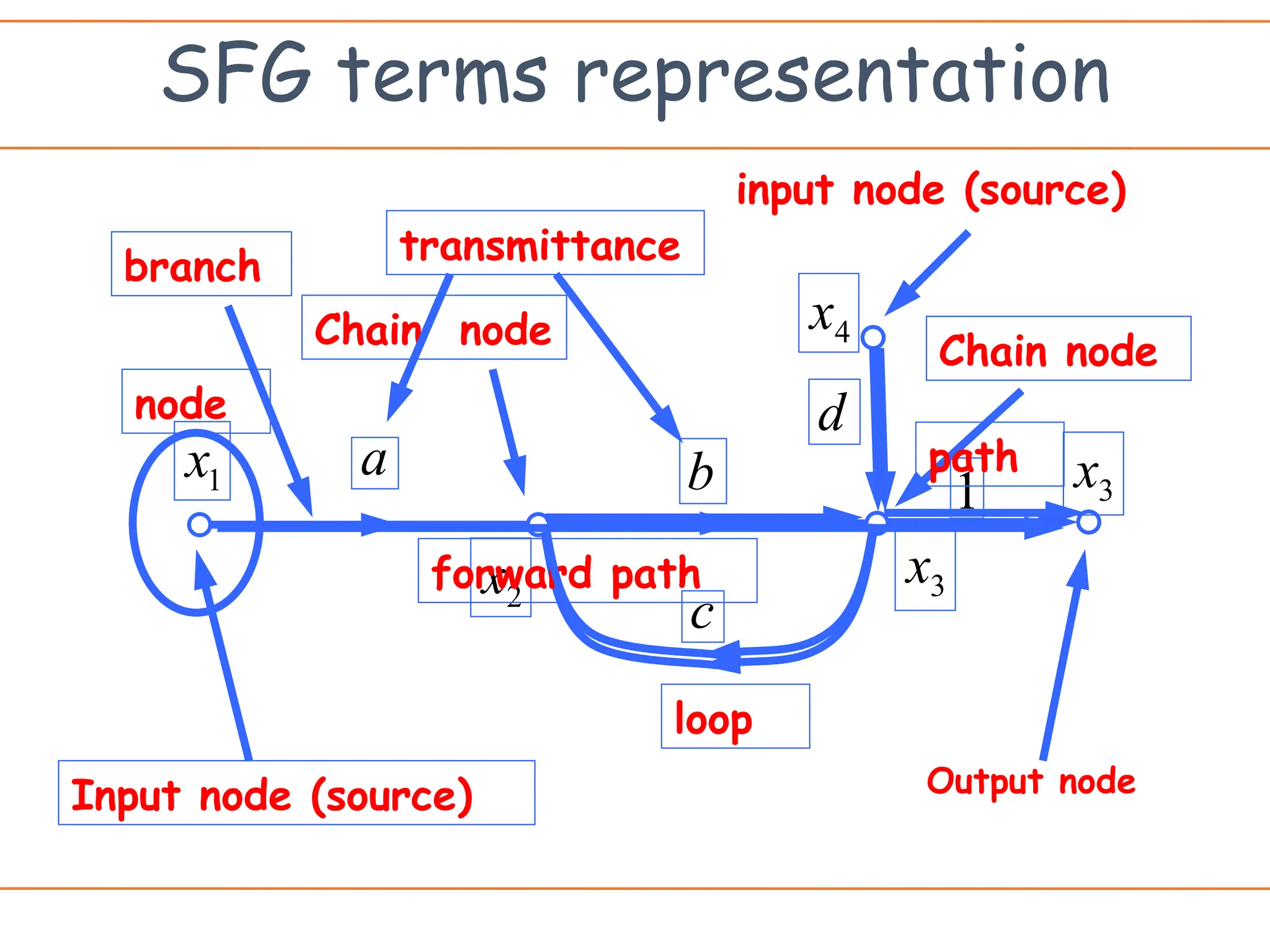
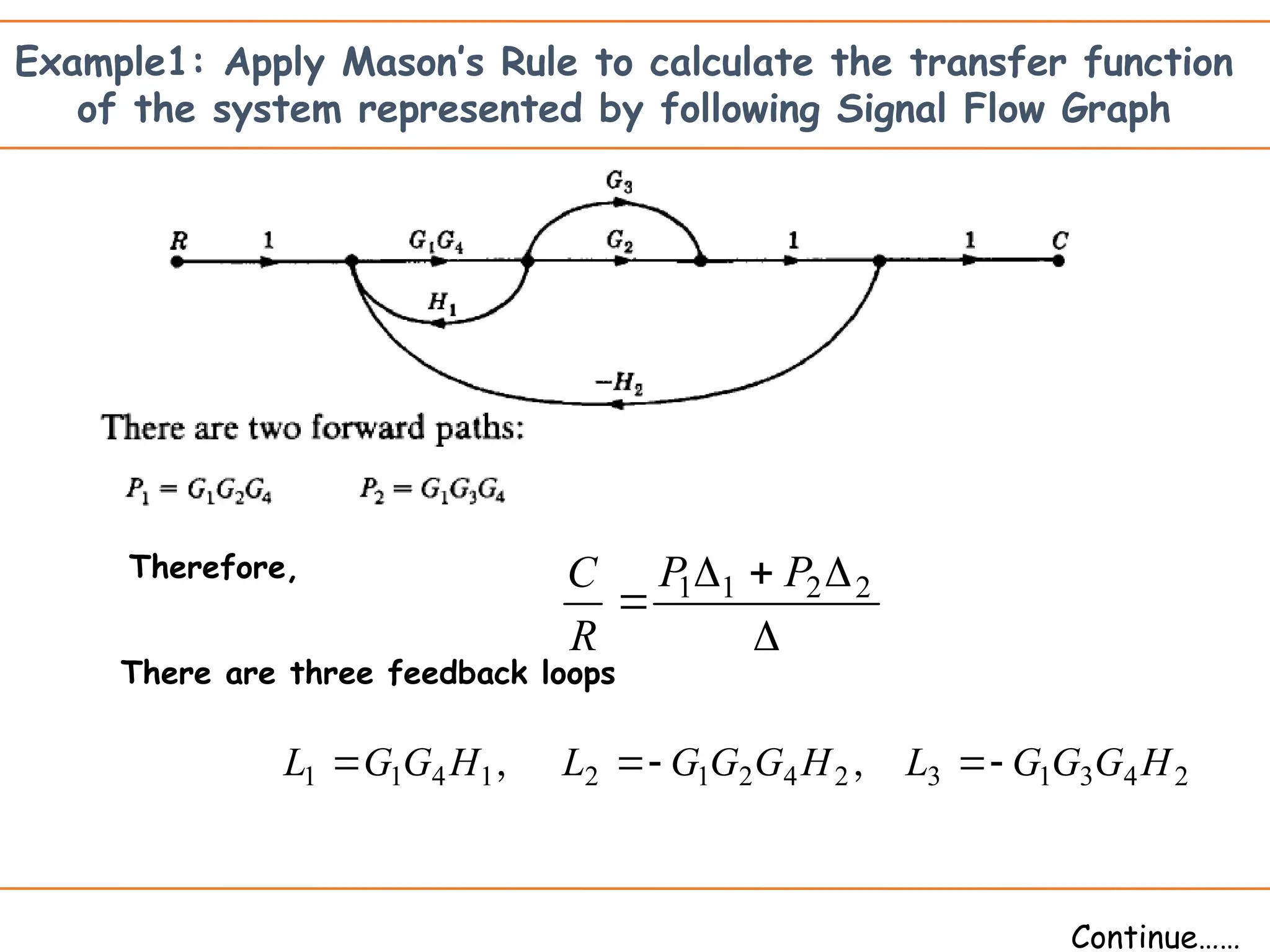
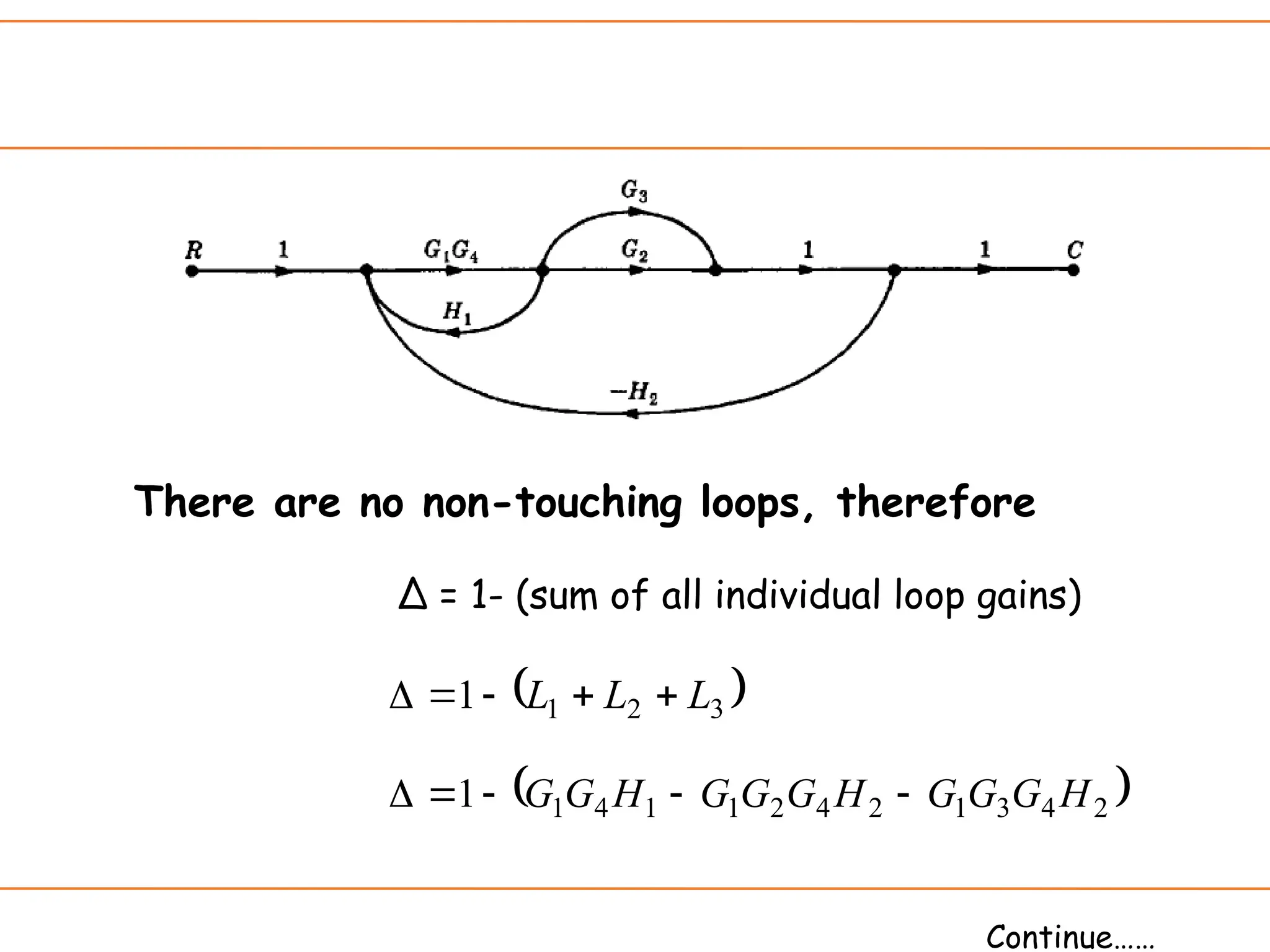
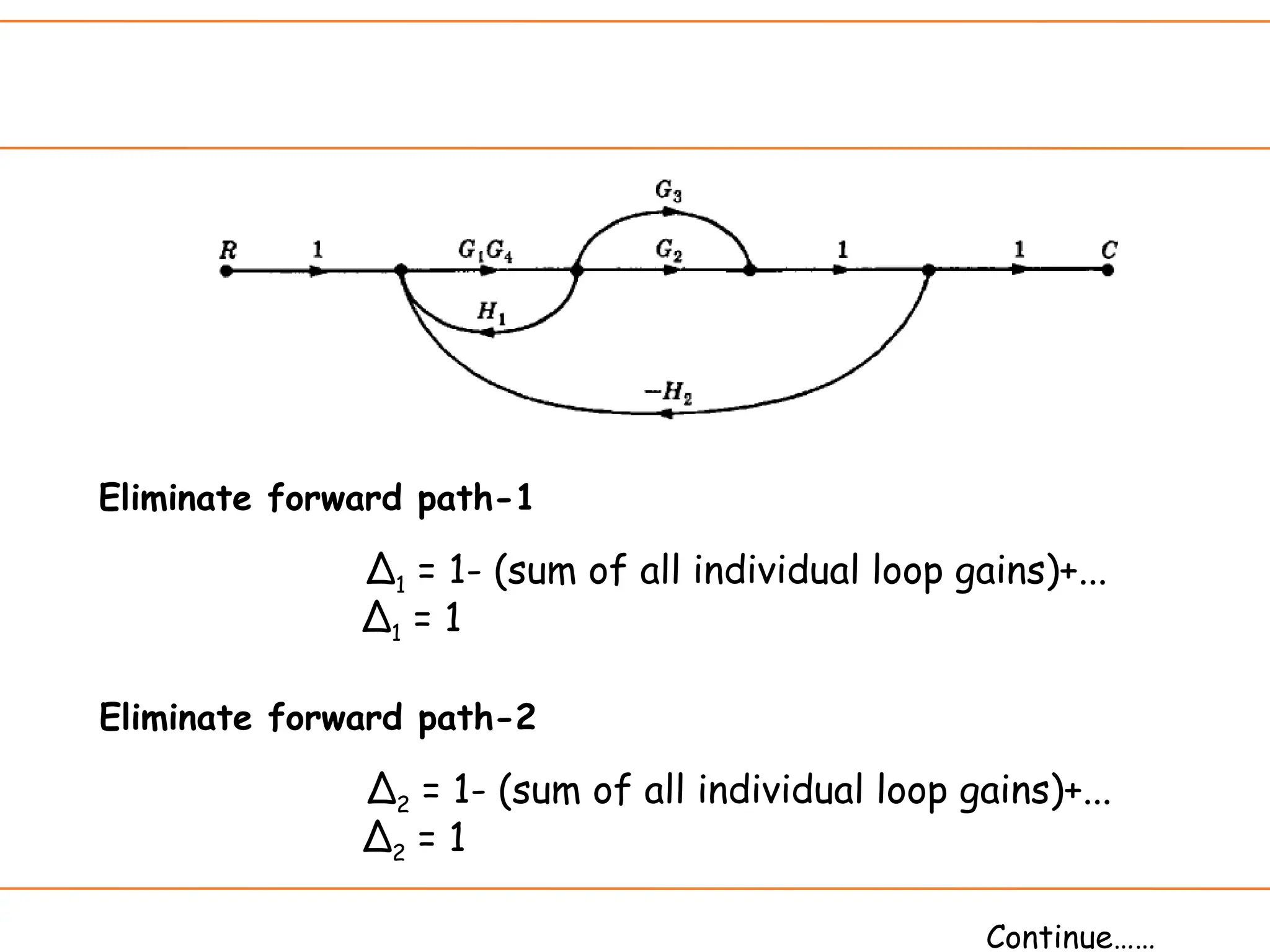
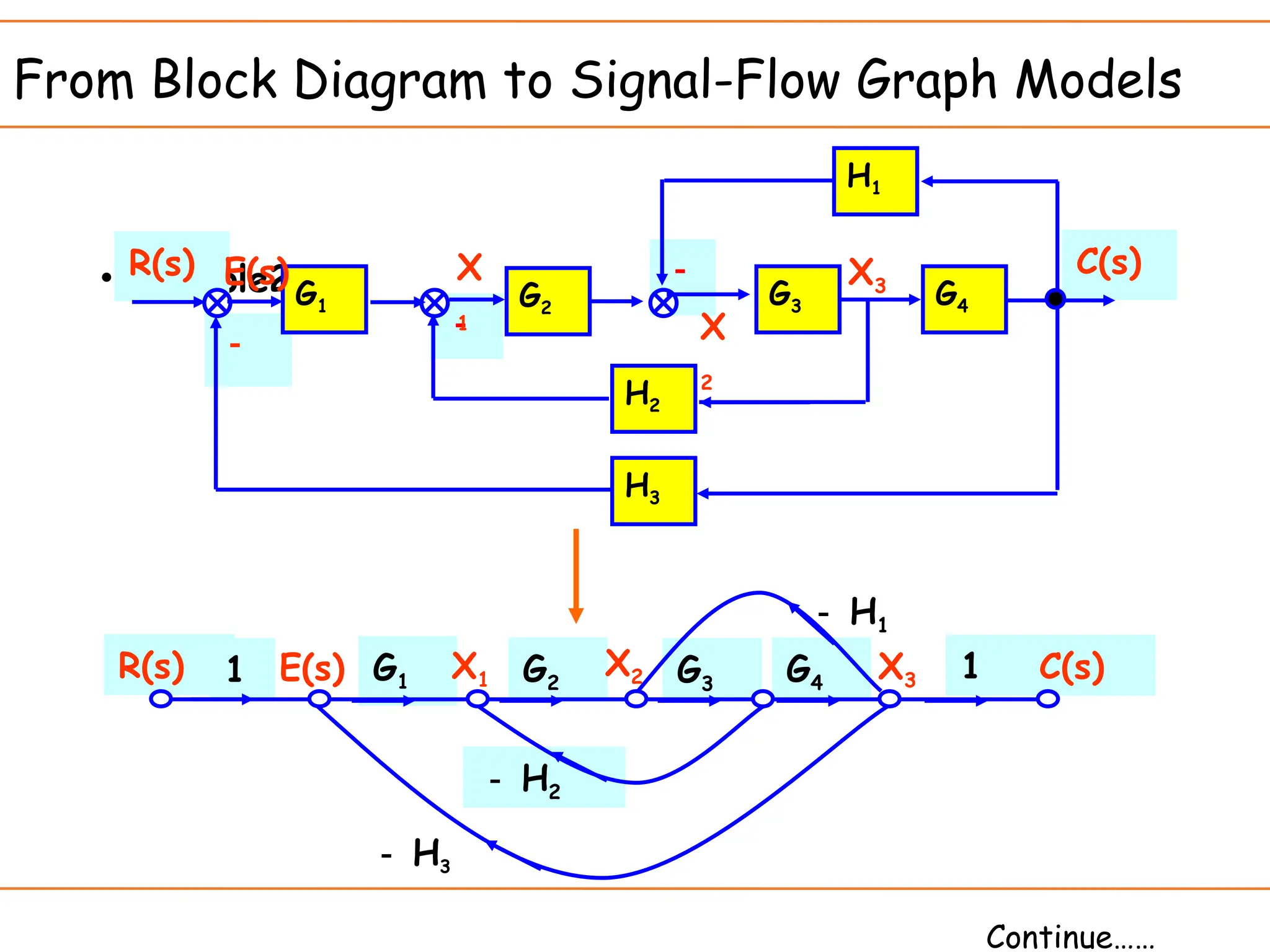
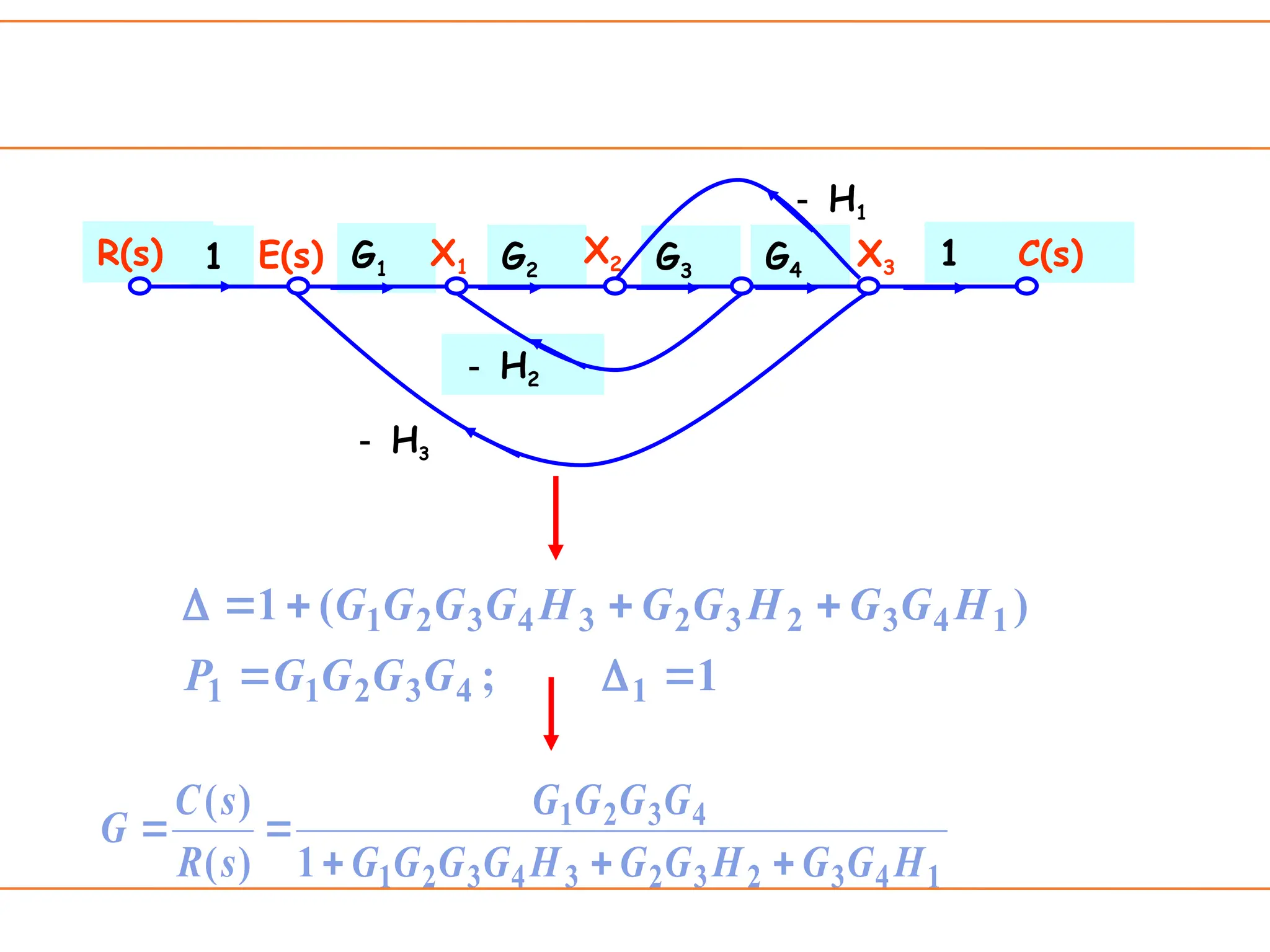
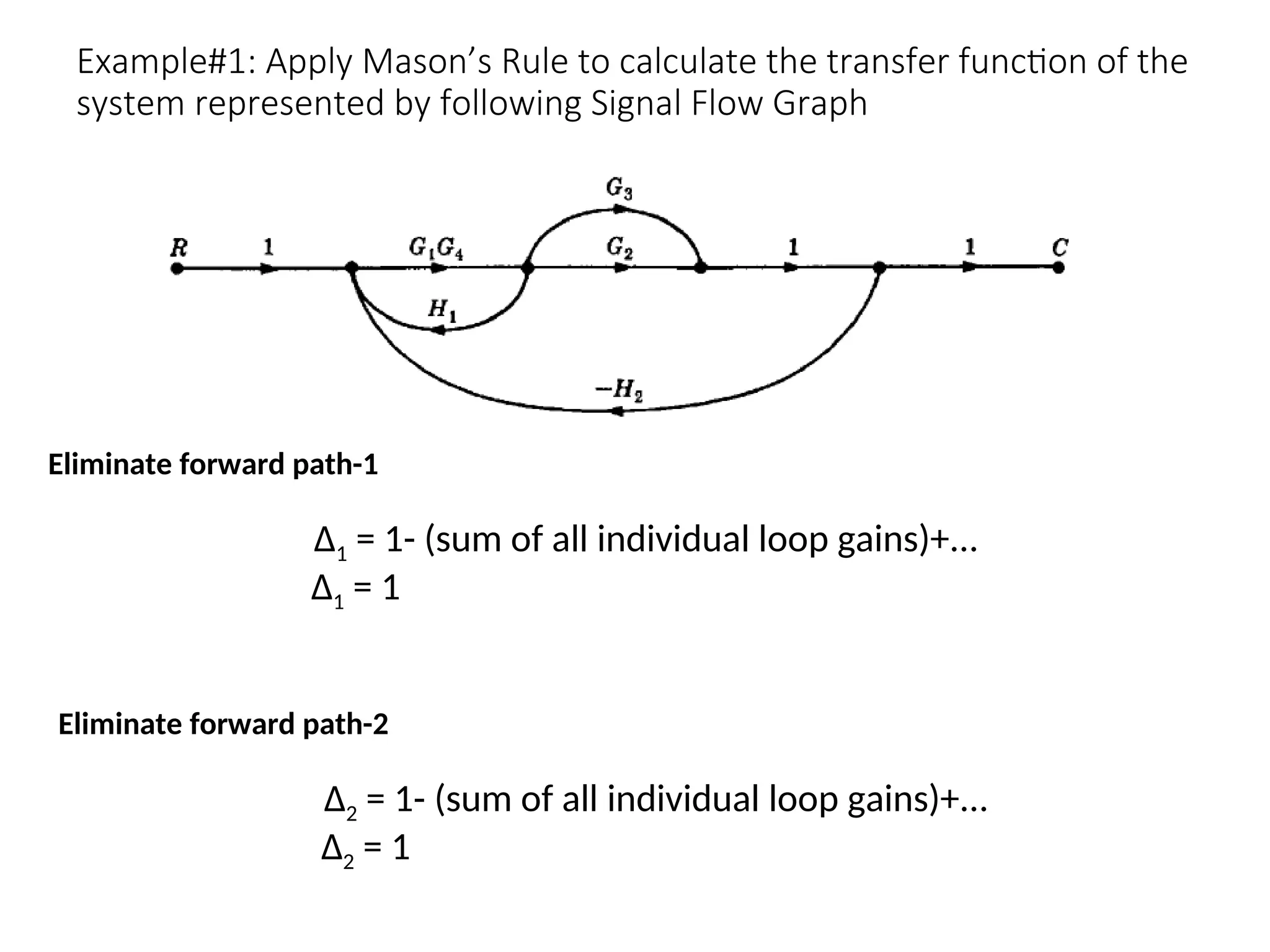
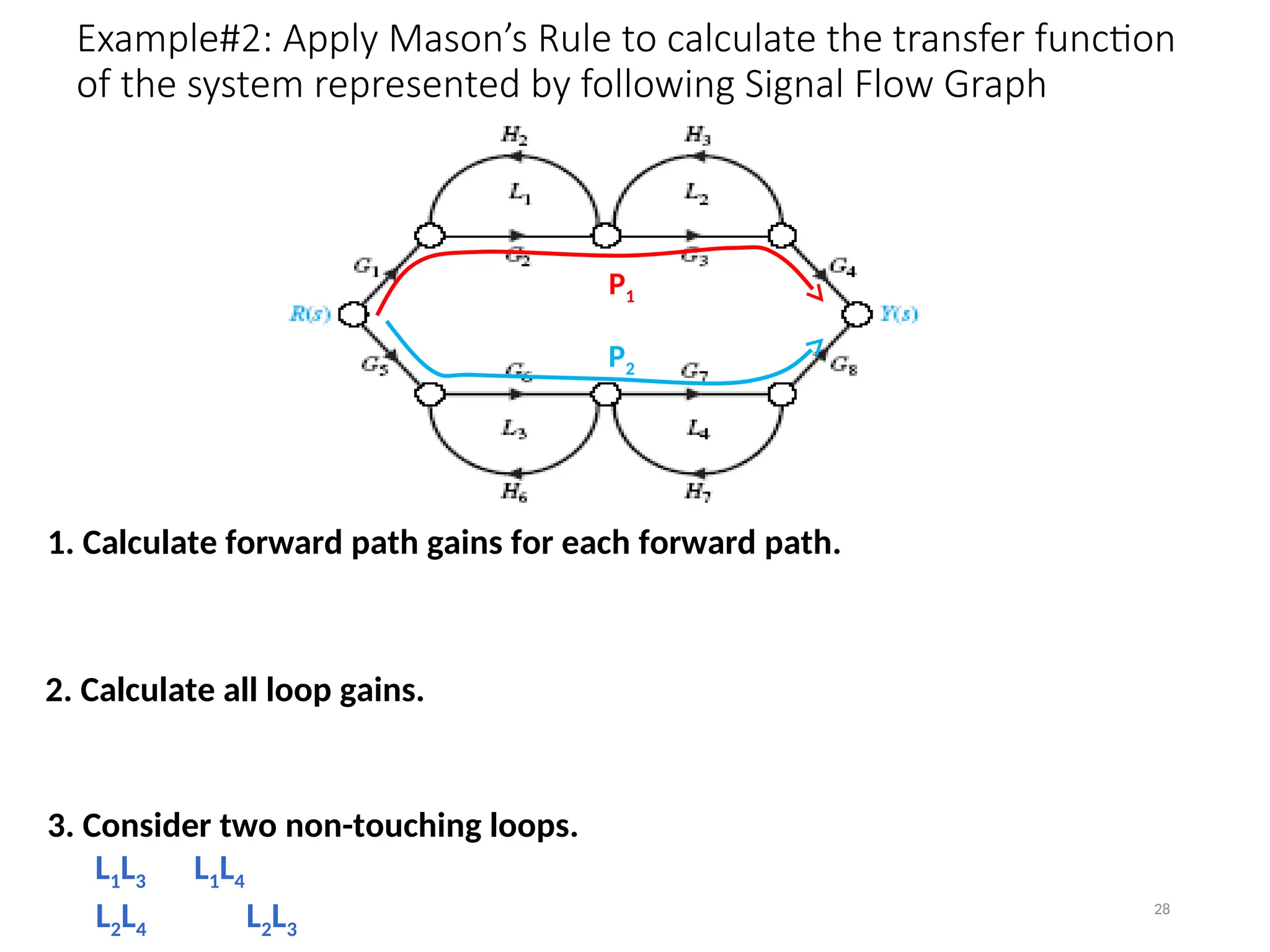
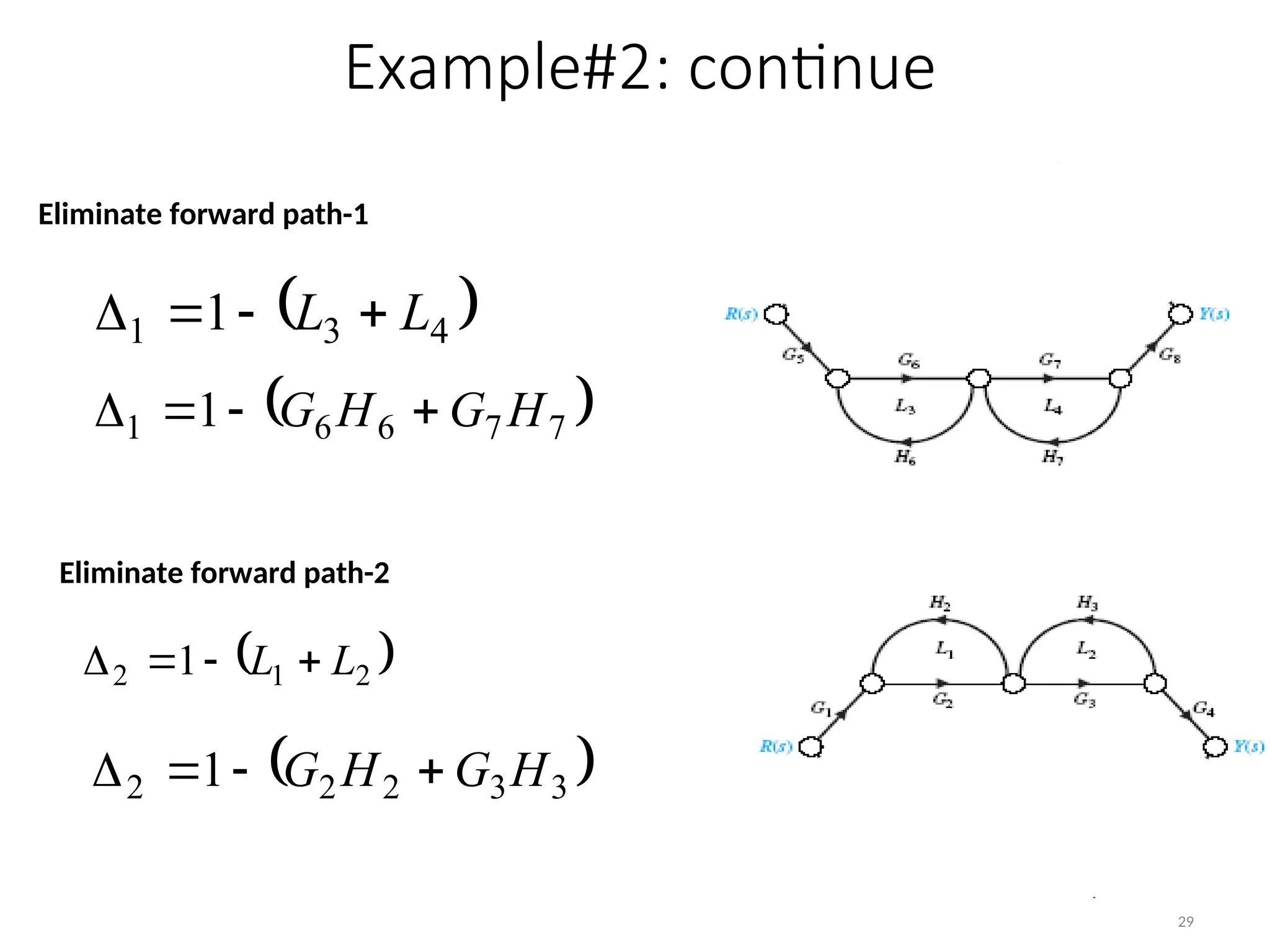
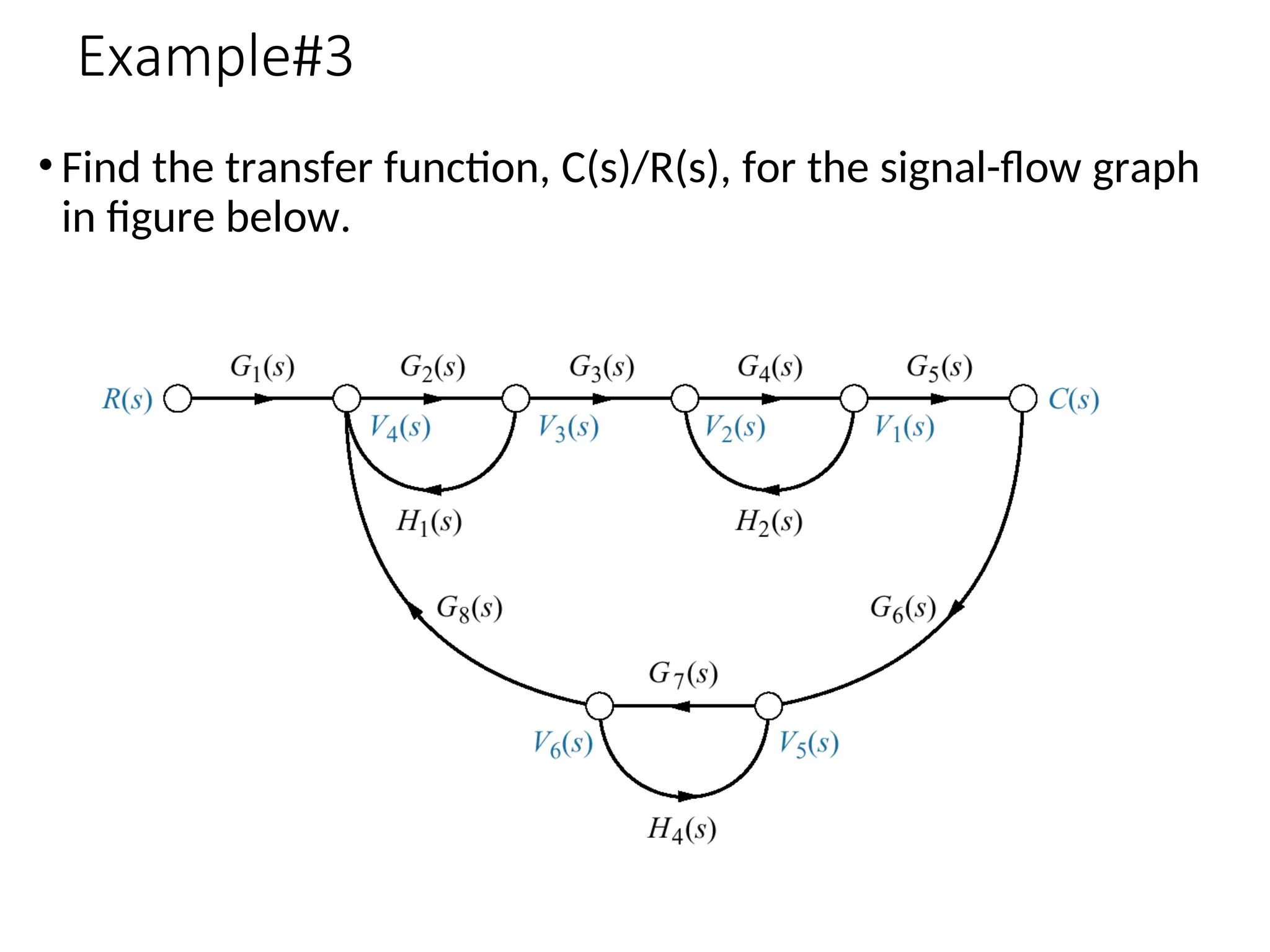
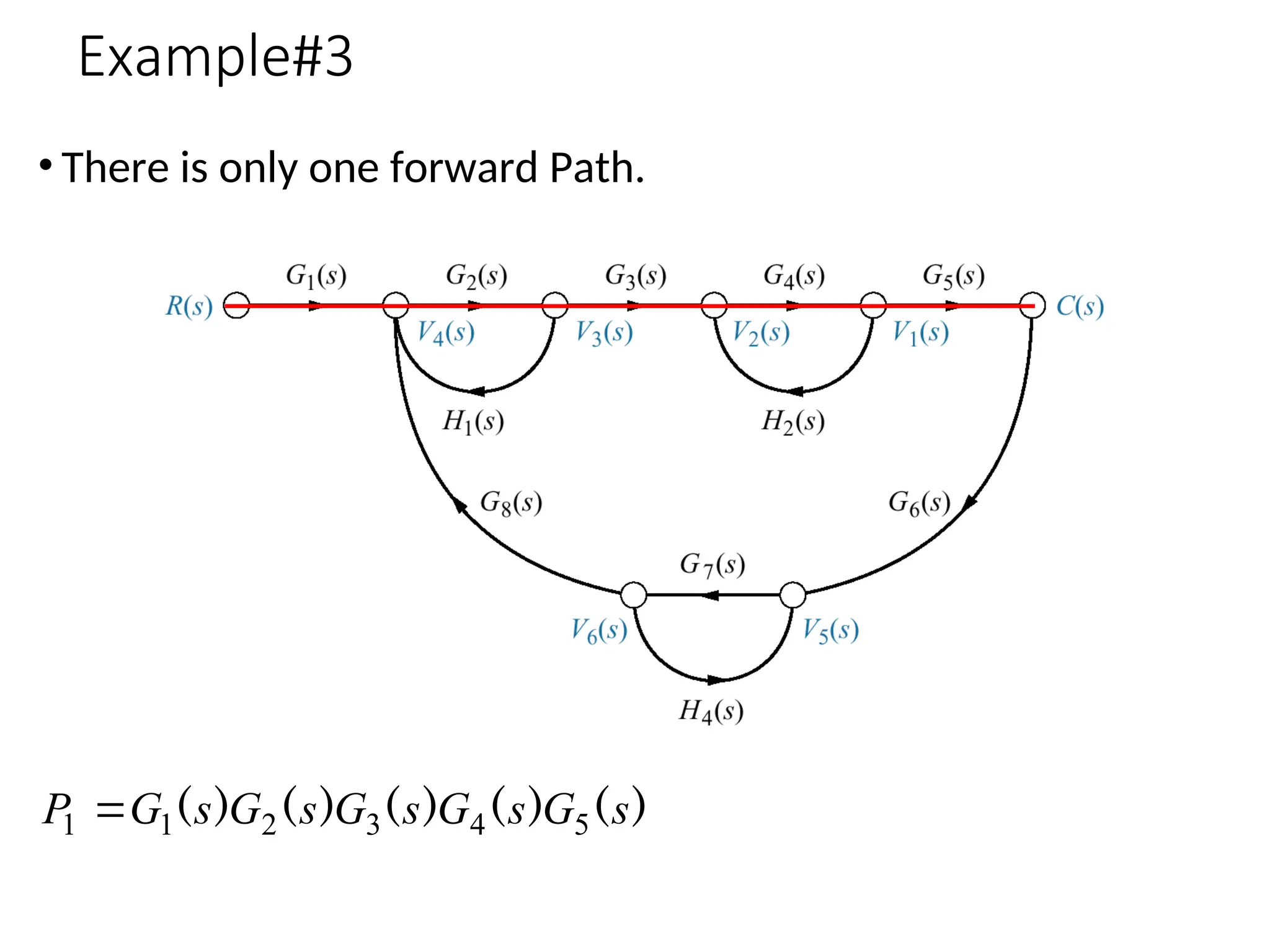
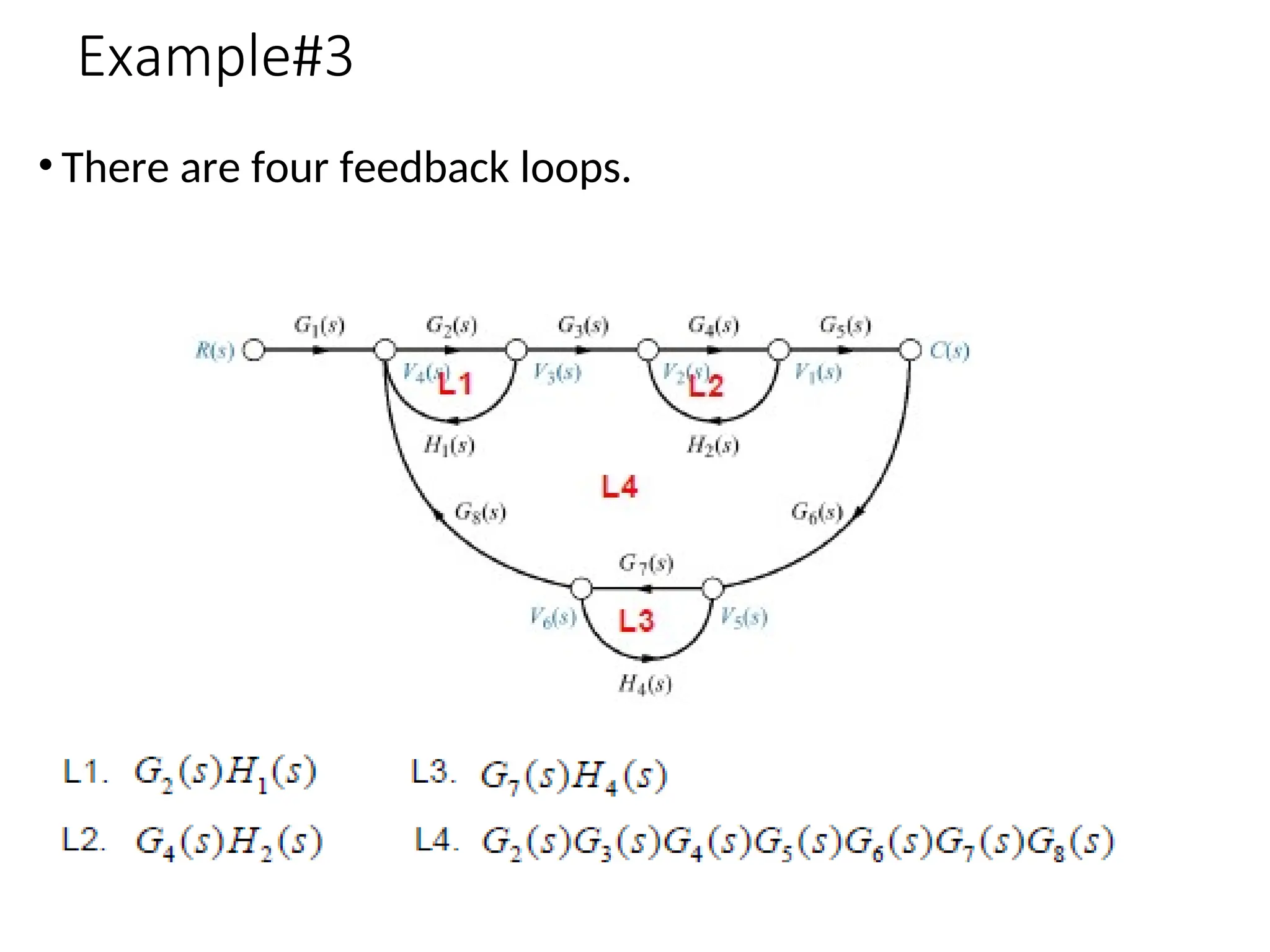
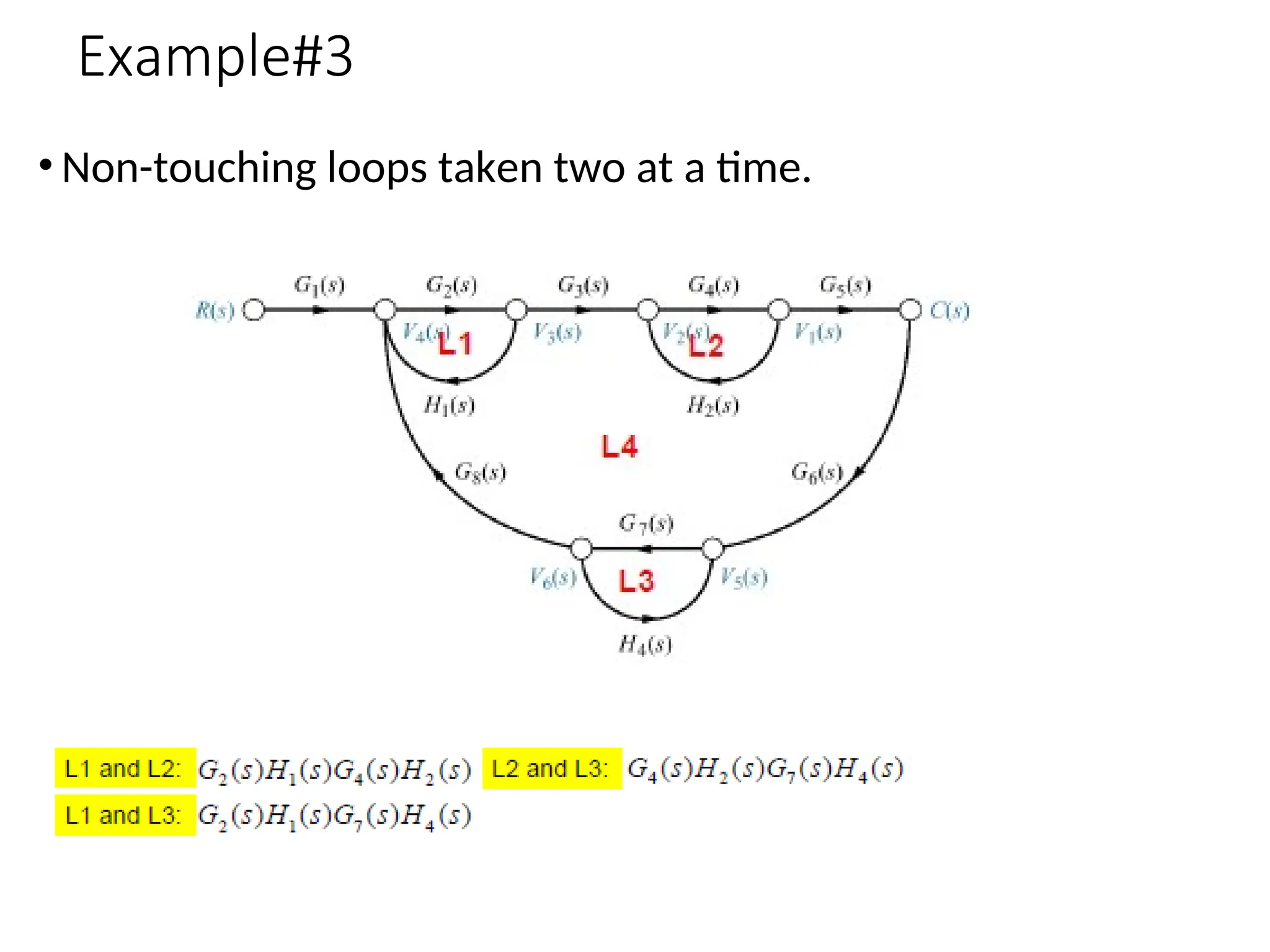
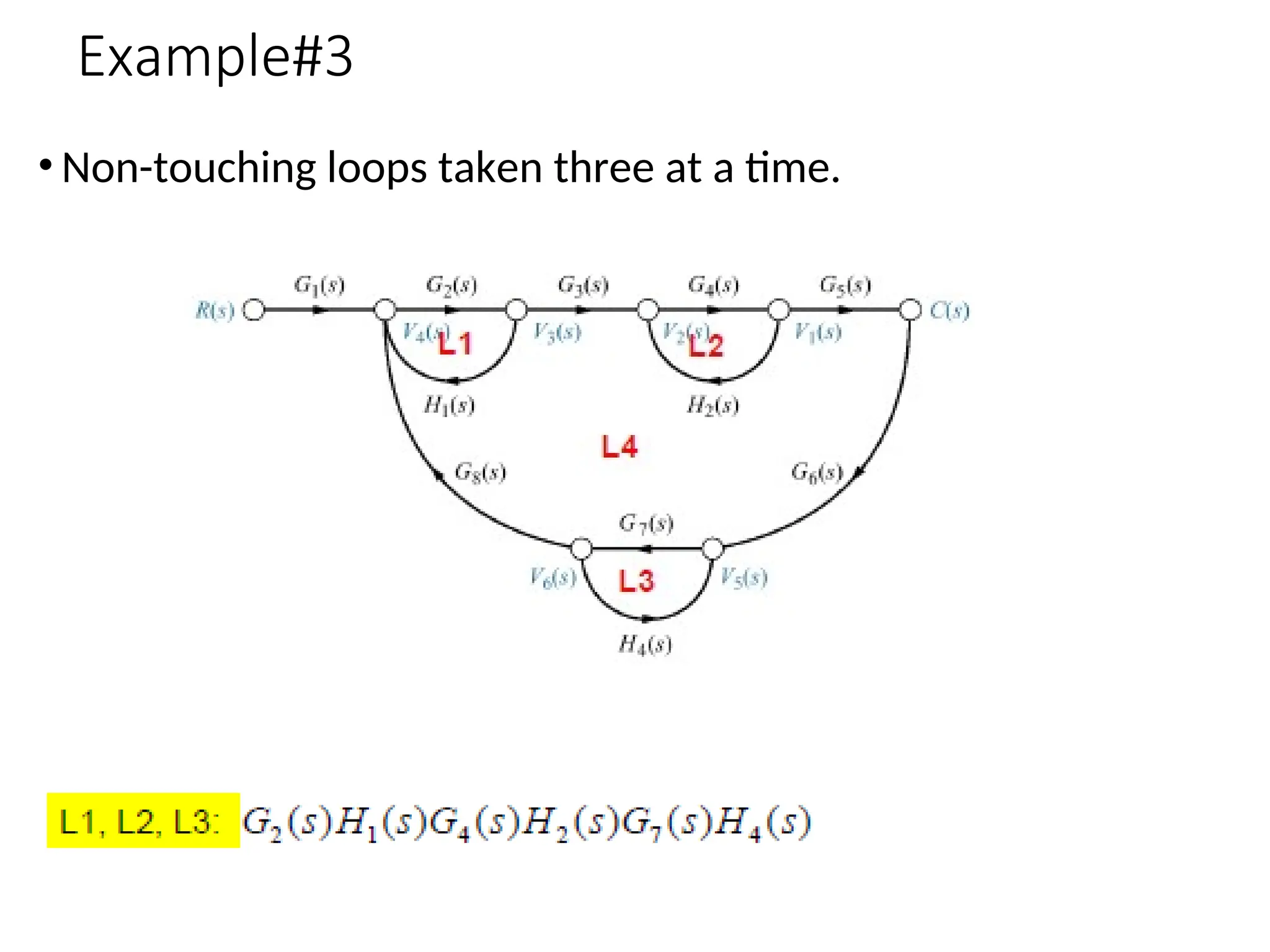
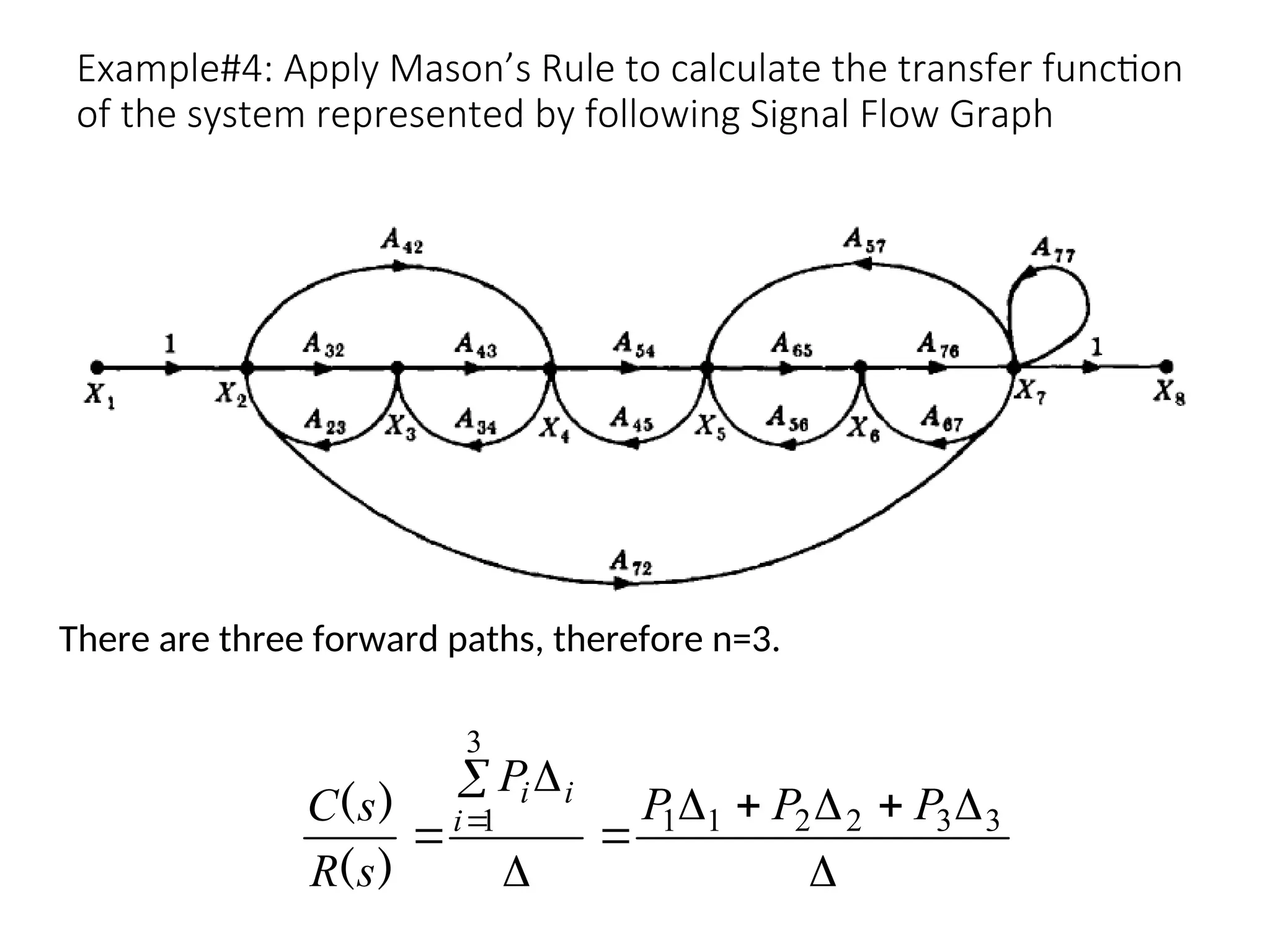
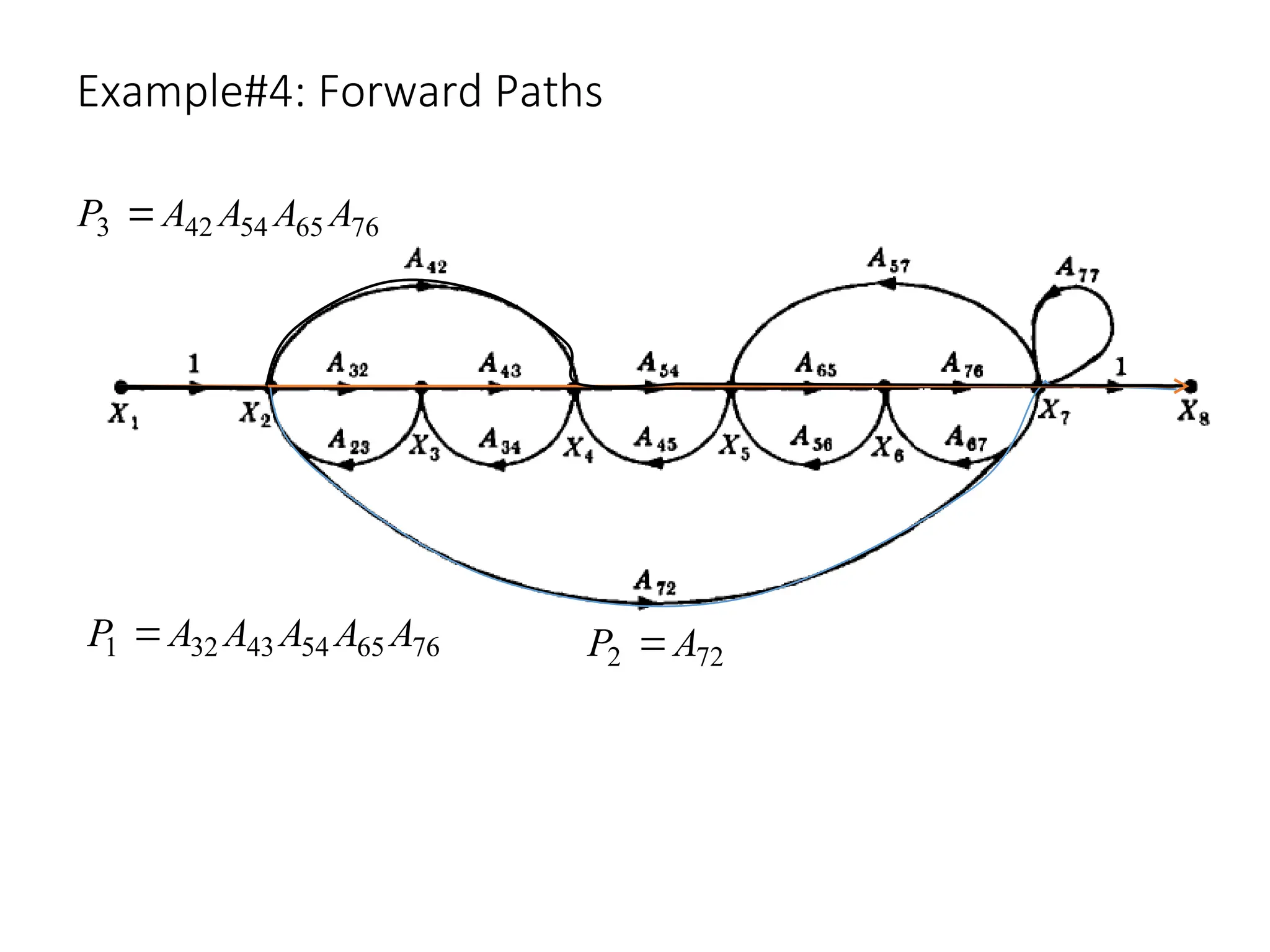
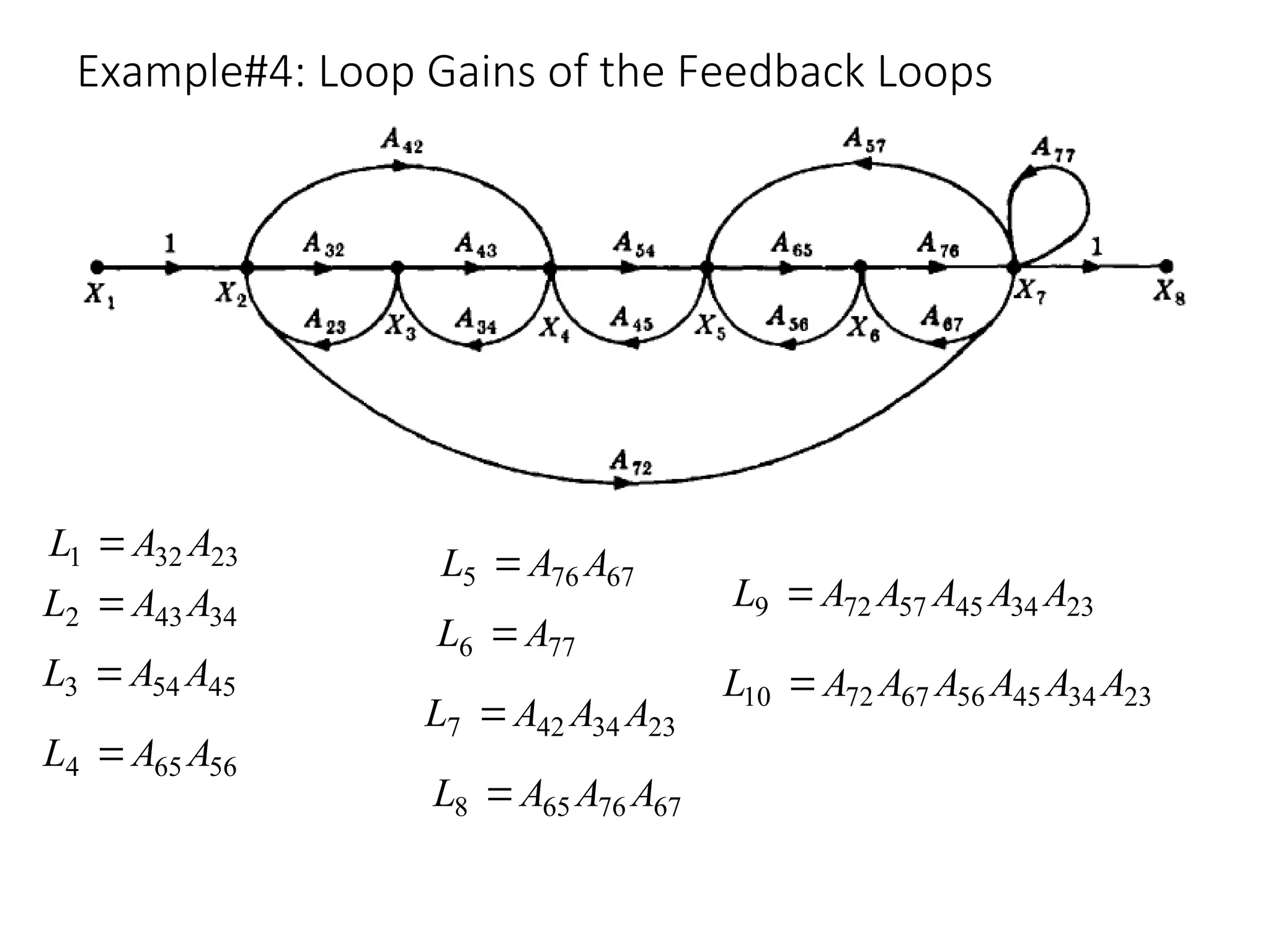
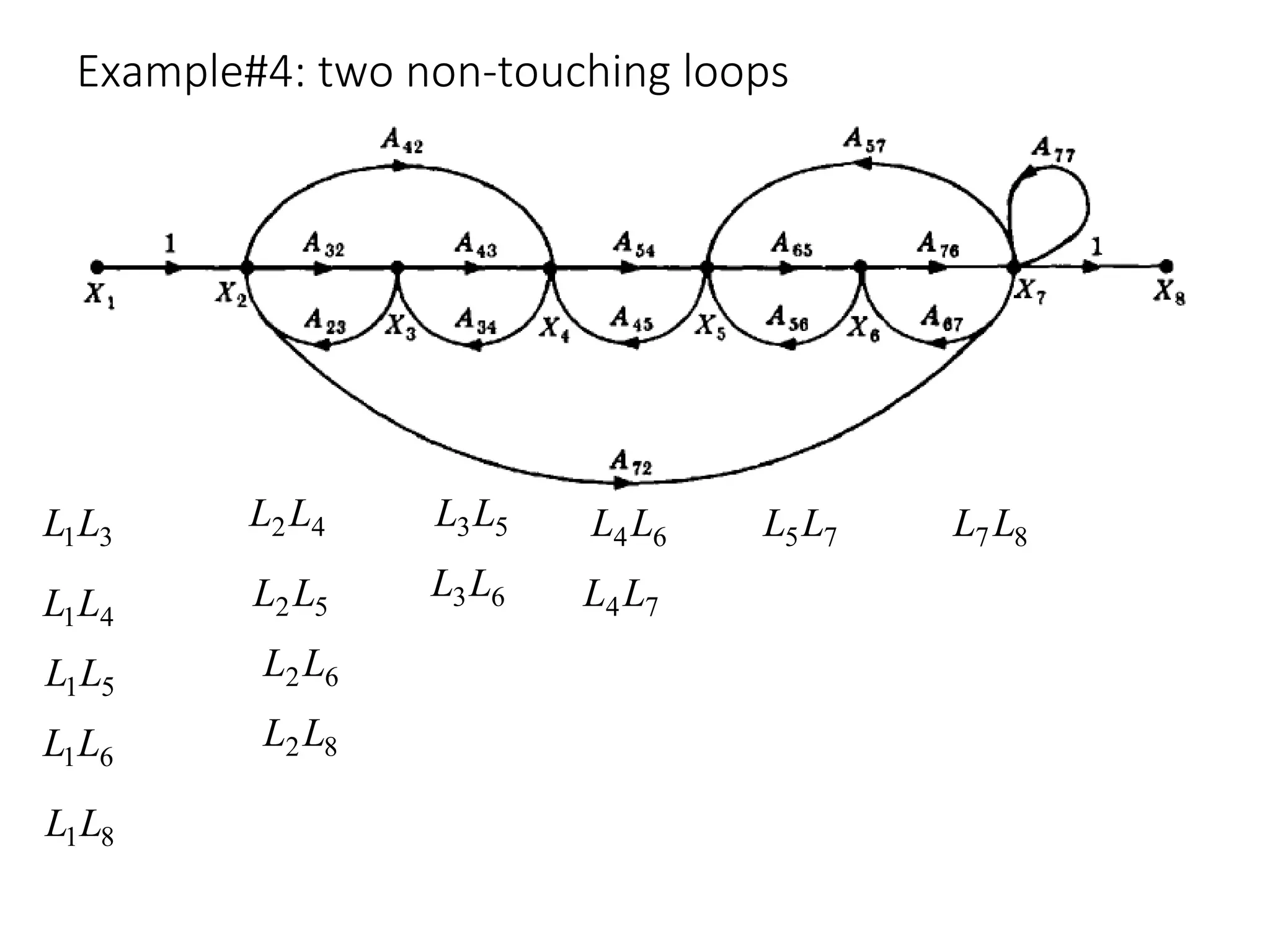
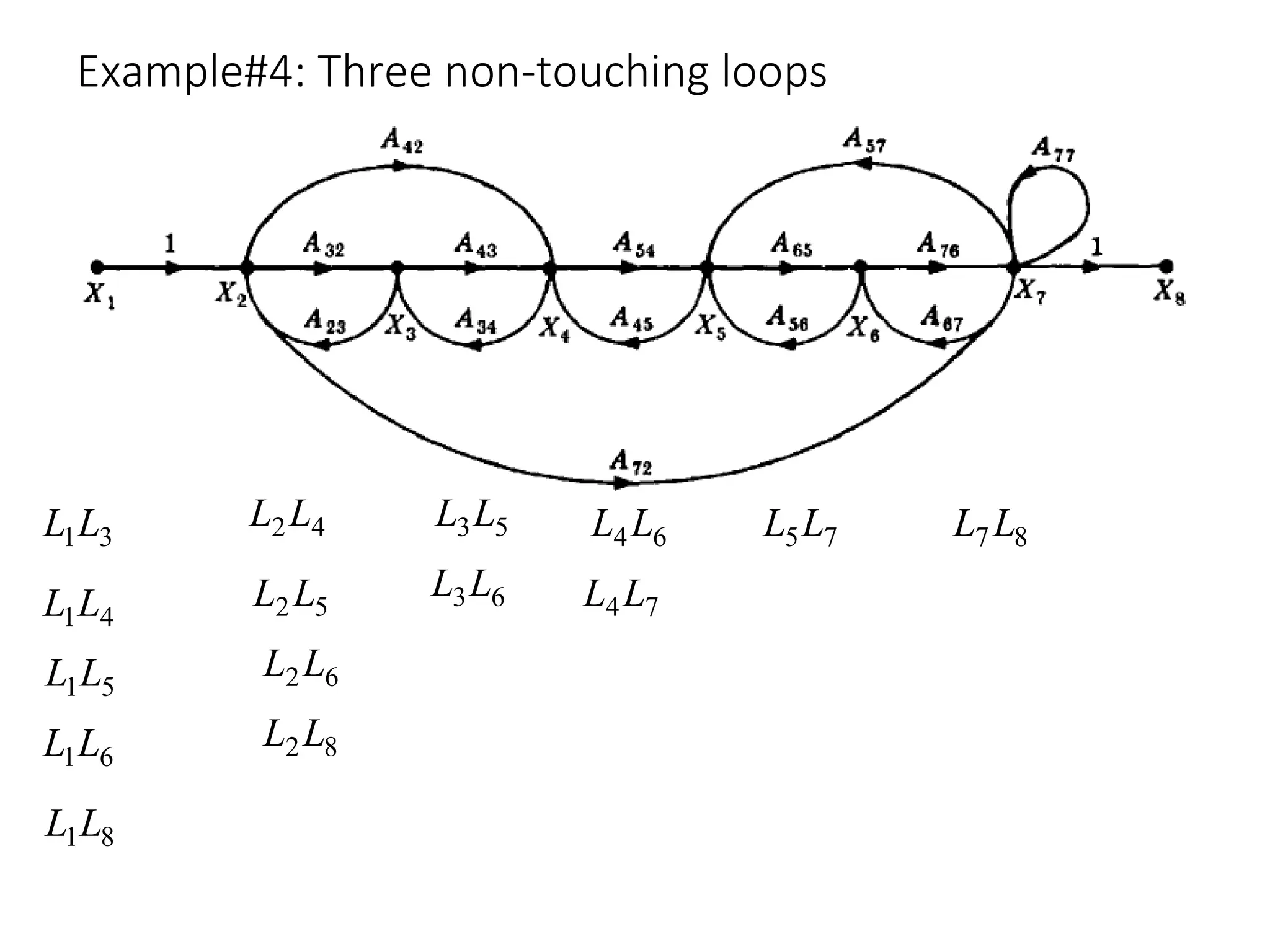
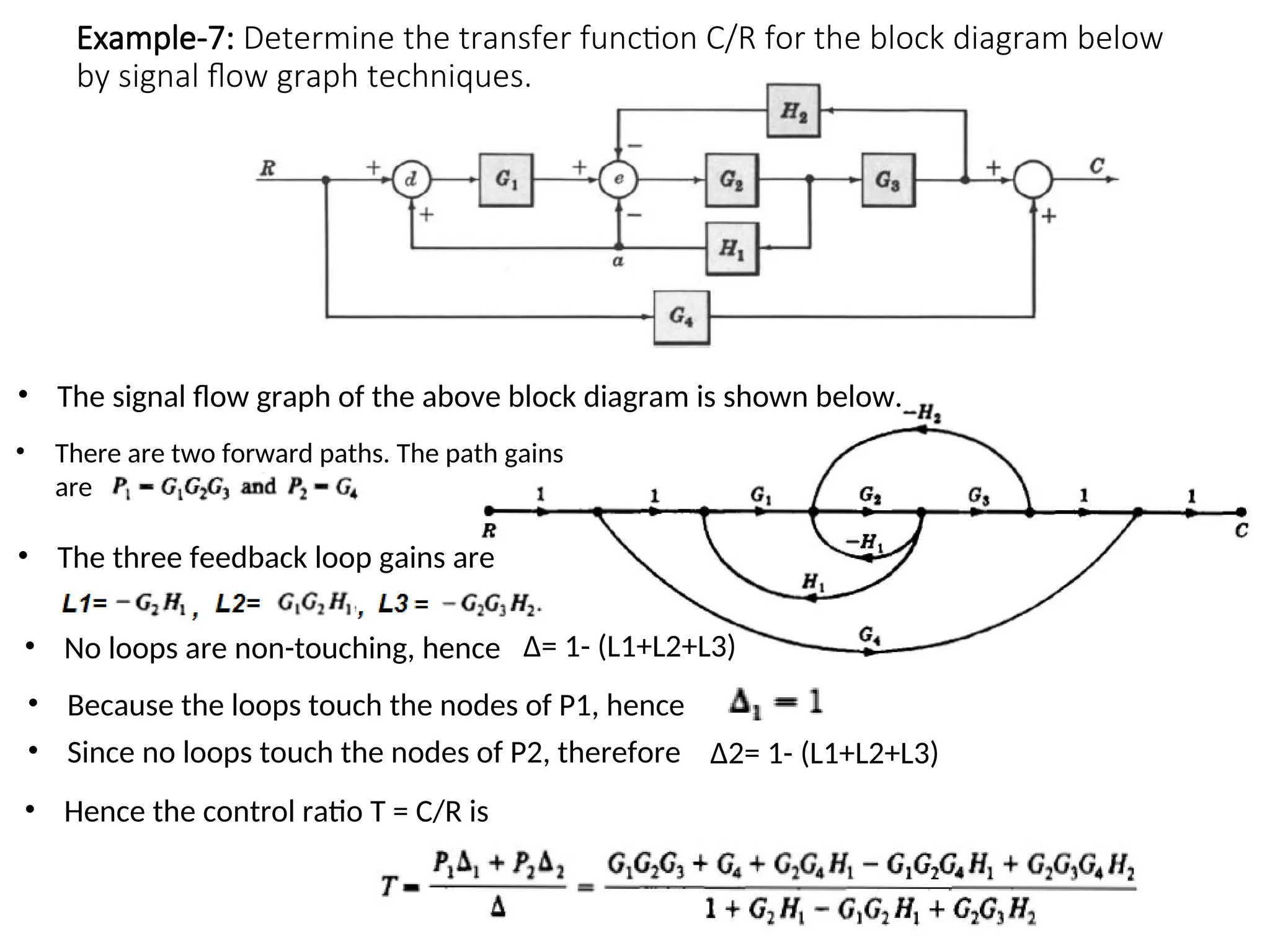
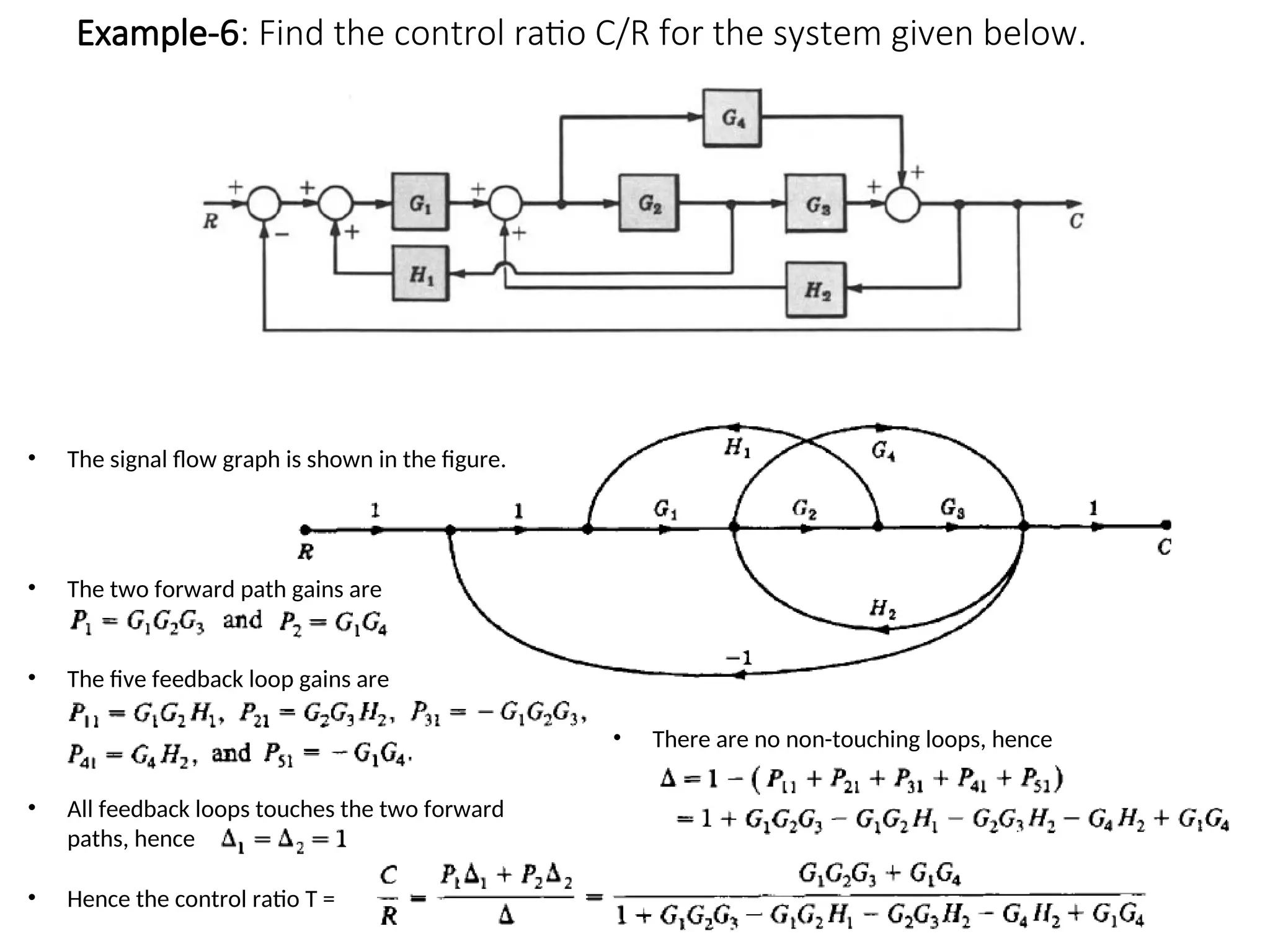
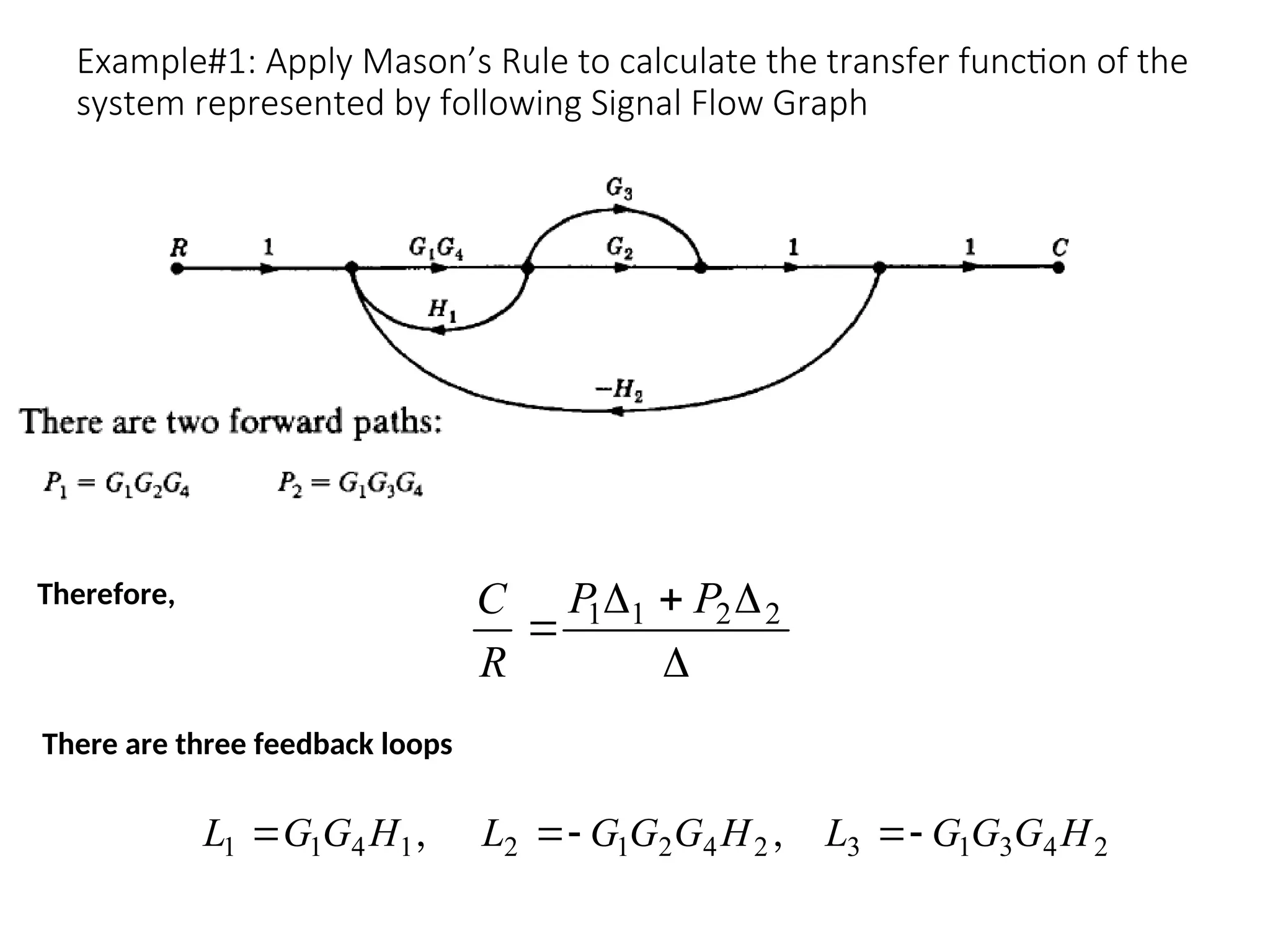
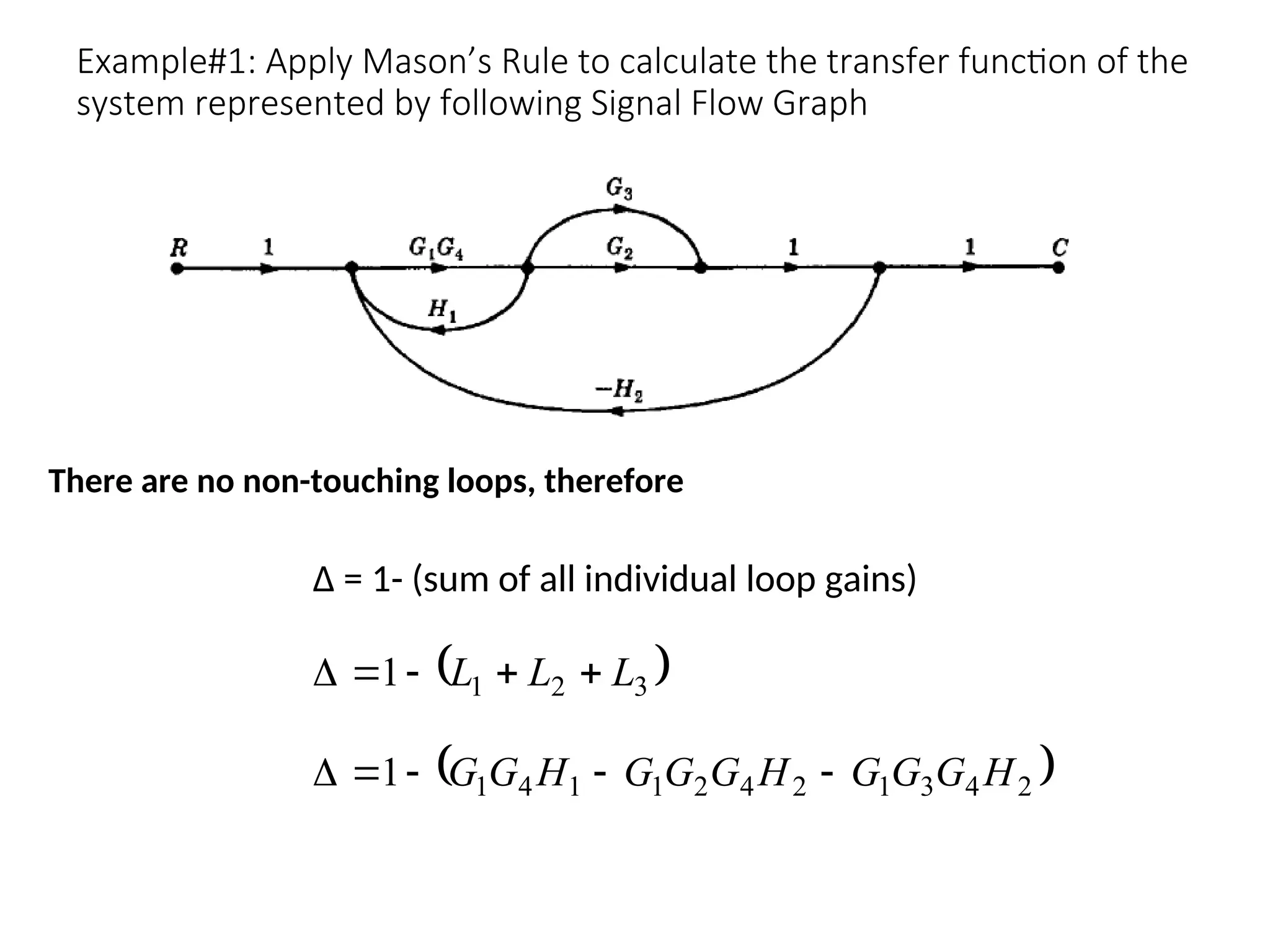
The document introduces signal flow graphs (SFG) as an alternative to block diagram representation in control engineering, explaining key concepts such as nodes, branches, and Mason's gain formula. It details the method for converting block diagrams to SFGs and provides multiple examples illustrating the application of Mason's rule for calculating transfer functions. Furthermore, it discusses important terminology related to paths and loops within the graphs, emphasizing the advantages of using SFGs for system analysis.

1. SIGNAL FLOW
GRAPH
CONTROL ENGINEERING FUNDAMENTALS
Eng. Mohammed Qasim Taha

2. Outline
•Introduction to Signal Flow Graphs
• Definitions
• Terminologies
•Mason’s Gain Formula
• Examples
•Signal Flow Graph from Block Diagrams
•Design Examples

3. Signal Flow Graph (SFG)
• Alternative method to block diagram
representation, developed by Samuel Jefferson
Mason.
• Advantage: the availability of a flow graph gain
formula, also called Mason’s gain formula.
• A signal-flow graph consists of a network in which
nodes are connected by directed branches.
• It depicts the flow of signals from one point of a
system to another and gives the relationships
among the signals.

4. Fundamentals of Signal Flow Graphs
ax
y 
x y
a
Consider a simple equation below and draw its signal
flow graph:
The signal flow graph of the equation is shown below;

5. Important terminology :
• Branches :-
line joining two nodes is called branch.
x y
a
Branch
• Dummy Nodes:-
A branch having one can be added at i/p as well as o/p.
Dummy Nodes

6. Out put node
Input node
b
x4
x3
x2
x1
x0 h
f
g
e
d
c
a
Input & output node
• Input node:-
It is node that has only outgoing branches.
• Output node:-
It is a node that has incoming branches.

7. Forward path:-
• Any path from i/p node to o/p node.
Forward path

8. Loop :-
• A closed path from a node to the same node is called
loop.

9. Self loop:-
•A feedback loop that contains of only one node is
called self loop.
Self loop

10. Loop gain:-
The product of all the gains forming a loop
Loop gain = A32 A23

11. Path & path gain
Path:-
A path is a traversal of connected branches in the
direction of branch arrow.
Path gain:-
The product of all branch gains while going through the
forward path it is called as path gain.

12. Feedback path or loop :-
• it is a path to o/p node to i/p node.

13. Touching loops:-
• when the loops are having the common node that the
loops are called touching loops.

14. Non touching loops:-
• when the loops are not having any common node
between them that are called as non- touching loops.

15. Non-touching loops for forward paths

16. Chain Node :-
• it is a node that has incoming as well as outgoing
branches.
Chain node

17. SFG terms representation
Input node (source)
b
1
x a
2
x
c
4
x
d
1
3
x
3
x
Chain node
Chain node
forward path
path
loop
branch
node
transmittance
input node (source)
Output node

18. Mason’s Rule (Mason, 1953)
• The block diagram reduction technique requires
successive application of fundamental relationships in
order to arrive at the system transfer function.
• On the other hand, Mason’s rule for reducing a
signal-flow graph to a single transfer function
requires the application of one formula.
• The formula was derived by S. J. Mason when he
related the signal-flow graph to the simultaneous
equations that can be written from the graph.

19. Mason’s Rule :-
• The transfer function, C(s)/R(s), of a system represented by a
signal-flow graph is;
• Where
• n = number of forward paths.
• Pi = the i th forward-path gain.
• ∆ = Determinant of the system
• ∆i = Determinant of the ith forward path

 
 
n
i
i
i
P
s
R
s
C 1
)
(
)
(

20. 
 
 
n
i
i
i
P
s
R
s
C 1
)
(
)
(
∆ is called the signal flow graph determinant or characteristic
function. Since ∆=0 is the system characteristic equation.
∆ = 1- (sum of all individual loop gains) + (sum of the products of
the gains of all possible two loops that do not touch each other) –
(sum of the products of the gains of all possible three loops that
do not touch each other) + … and so forth with sums of higher
number of non-touching loop gains
∆i = value of Δ for the part of the block diagram that does not
touch the i-th forward path (Δi = 1 if there are no non-touching
loops to the i-th path.)

21. Example1: Apply Mason’s Rule to calculate the transfer function
of the system represented by following Signal Flow Graph




 2
2
1
1 P
P
R
C
Therefore,
2
4
3
1
3
2
4
2
1
2
1
4
1
1 H
G
G
G
L
H
G
G
G
L
H
G
G
L 



 ,
,
There are three feedback loops
Continue……

22. ∆ = 1- (sum of all individual loop gains)
There are no non-touching loops, therefore
 
2
4
3
1
2
4
2
1
1
4
1
1 H
G
G
G
H
G
G
G
H
G
G 




 
3
2
1
1 L
L
L 




Continue……

23. ∆2 = 1- (sum of all individual loop gains)+...
Eliminate forward path-2
∆2 = 1
∆1 = 1- (sum of all individual loop gains)+...
Eliminate forward path-1
∆1 = 1
Continue……

25. From Block Diagram to Signal-Flow Graph Models
• Example2
－
－
－
C(s)
R(s)
G1 G2
H2
H1
G4
G3
H3
E(s) X
1 X
2
X3
R(s)
－ H2
1
G4
G3
G2
G1
1 C(s)
－ H1
－ H3
X1
X2 X3
E(s)
Continue……

26. R(s)
－ H2
1
G4
G3
G2
G1
1 C(s)
－ H1
－ H3
X1
X2 X3
E(s)
1
4
3
2
3
2
3
4
3
2
1
4
3
2
1
1
)
(
)
(
H
G
G
H
G
G
H
G
G
G
G
G
G
G
G
s
R
s
C
G





1
;
)
(
1
1
4
3
2
1
1
1
4
3
2
3
2
3
4
3
2
1








G
G
G
G
P
H
G
G
H
G
G
H
G
G
G
G

27. Example#1: Apply Mason’s Rule to calculate the transfer function of the
system represented by following Signal Flow Graph
∆1 = 1- (sum of all individual loop gains)+...
Eliminate forward path-1
∆1 = 1
∆2 = 1- (sum of all individual loop gains)+...
Eliminate forward path-2
∆2 = 1

28. 28
Example#2: Apply Mason’s Rule to calculate the transfer function
of the system represented by following Signal Flow Graph
2. Calculate all loop gains.
3. Consider two non-touching loops.
L1L3 L1L4
L2L4 L2L3
1. Calculate forward path gains for each forward path.
P1
P2

29. 29
Example#2: continue
Eliminate forward path-1
 
4
3
1 1 L
L 



 
2
1
2 1 L
L 



Eliminate forward path-2
 
7
7
6
6
1 1 H
G
H
G 



 
3
3
2
2
2 1 H
G
H
G 




30. Example#3
• Find the transfer function, C(s)/R(s), for the signal-flow graph
in figure below.

31. Example#3
• There is only one forward Path.
)
(
)
(
)
(
)
(
)
( s
G
s
G
s
G
s
G
s
G
P 5
4
3
2
1
1 

32. Example#3
• There are four feedback loops.

33. Example#3
• Non-touching loops taken two at a time.

34. Example#3
• Non-touching loops taken three at a time.

35. Example#3
Eliminate forward path-1

36. Example#4: Apply Mason’s Rule to calculate the transfer function
of the system represented by following Signal Flow Graph








 
  3
3
2
2
1
1
3
1 P
P
P
P
s
R
s
C i
i
i
)
(
)
(
There are three forward paths, therefore n=3.

37. Example#4: Forward Paths
72
2 A
P 
76
65
54
43
32
1 A
A
A
A
A
P 
76
65
54
42
3 A
A
A
A
P 

38. Example#4: Loop Gains of the Feedback Loops
23
32
1 A
A
L 
34
43
2 A
A
L 
45
54
3 A
A
L 
56
65
4 A
A
L 
67
76
5 A
A
L 
77
6 A
L 
23
34
42
7 A
A
A
L 
67
76
65
8 A
A
A
L 
23
34
45
57
72
9 A
A
A
A
A
L 
23
34
45
56
67
72
10 A
A
A
A
A
A
L 

39. Example#4: two non-touching loops
3
1L
L
4
1L
L
5
1L
L
6
1L
L
8
1L
L
4
2L
L
5
2L
L
6
2L
L
8
2L
L
5
3L
L
6
3L
L
6
4L
L
7
4L
L
7
5L
L 8
7 L
L

40. Example#4: Three non-touching loops
3
1L
L
4
1L
L
5
1L
L
6
1L
L
8
1L
L
4
2L
L
5
2L
L
6
2L
L
8
2L
L
5
3L
L
6
3L
L
6
4L
L
7
4L
L
7
5L
L 8
7 L
L

41. G1 G4
G3
From Block Diagram to Signal-Flow Graph Models
Example#5
－
－
－
C(s)
R(s)
G1 G2
H2
H1
G4
G3
H3
E(s) X1
X2
X3
R(s) C(s)
－ H2
－ H1
－ H3
X1
X2 X3
E(s)
1 G2

42. 1
;
)
(
1
1
4
3
2
1
1
1
4
3
2
3
2
3
4
3
2
1








G
G
G
G
P
H
G
G
H
G
G
H
G
G
G
G
1
4
3
2
3
2
3
4
3
2
1
4
3
2
1
1
)
(
)
(
H
G
G
H
G
G
H
G
G
G
G
G
G
G
G
s
R
s
C
G





R(s)
－ H2
1
G4
G3
G2
G1
1 C(s)
－ H1
－ H3
X1
X2 X3
E(s)
From Block Diagram to Signal-Flow Graph Models
Example#5

43. Example#6
We have
2
1
2
2
1
1
2
4
2
1
2
G
G
G
G
G
G
G
p
s
R
s
C k
k






 

)
(
)
(

44. Example-7: Determine the transfer function C/R for the block diagram below
by signal flow graph techniques.
• The signal flow graph of the above block diagram is shown below.
• There are two forward paths. The path gains
are
• The three feedback loop gains are
• No loops are non-touching, hence
• Since no loops touch the nodes of P2, therefore
• Because the loops touch the nodes of P1, hence
• Hence the control ratio T = C/R is
Δ= 1- (L1+L2+L3)
Δ2= 1- (L1+L2+L3)

45. Example-6: Find the control ratio C/R for the system given below.
• The two forward path gains are
• The signal flow graph is shown in the figure.
• The five feedback loop gains are
• Hence the control ratio T =
• There are no non-touching loops, hence
• All feedback loops touches the two forward
paths, hence

46. Example#1: Apply Mason’s Rule to calculate the transfer function of the
system represented by following Signal Flow Graph




 2
2
1
1 P
P
R
C
Therefore,
2
4
3
1
3
2
4
2
1
2
1
4
1
1 H
G
G
G
L
H
G
G
G
L
H
G
G
L 



 ,
,
There are three feedback loops

47. Example#1: Apply Mason’s Rule to calculate the transfer function of the
system represented by following Signal Flow Graph
∆ = 1- (sum of all individual loop gains)
There are no non-touching loops, therefore
 
3
2
1
1 L
L
L 




 
2
4
3
1
2
4
2
1
1
4
1
1 H
G
G
G
H
G
G
G
H
G
G 





48. Example#1: Continue

49. 4. Consider three non-touching loops.
None.
5. Calculate Δ from steps 2,3,4.
   
4
2
3
2
4
1
3
1
4
3
2
1
1 L
L
L
L
L
L
L
L
L
L
L
L 









49
 
 
7
7
3
3
6
6
3
3
7
7
2
2
6
6
2
2
7
7
6
6
3
3
2
2
1
H
G
G
H
H
G
G
H
H
G
H
G
H
G
H
G
H
G
H
G
G
H
H
G










Example#2: continue

50. 



 2
2
1
1 P
P
s
R
s
Y
)
(
)
(
50
Example#2: continue
 
   
 
   
7
7
3
3
6
6
3
3
7
7
2
2
6
6
2
2
7
7
6
6
3
3
2
2
3
3
2
2
8
7
6
5
7
7
6
6
4
3
2
1
1
1
1
H
G
G
H
H
G
G
H
H
G
H
G
H
G
H
G
H
G
H
G
G
H
H
G
H
G
H
G
G
G
G
G
H
G
H
G
G
G
G
G
s
R
s
Y














)
(
)
(