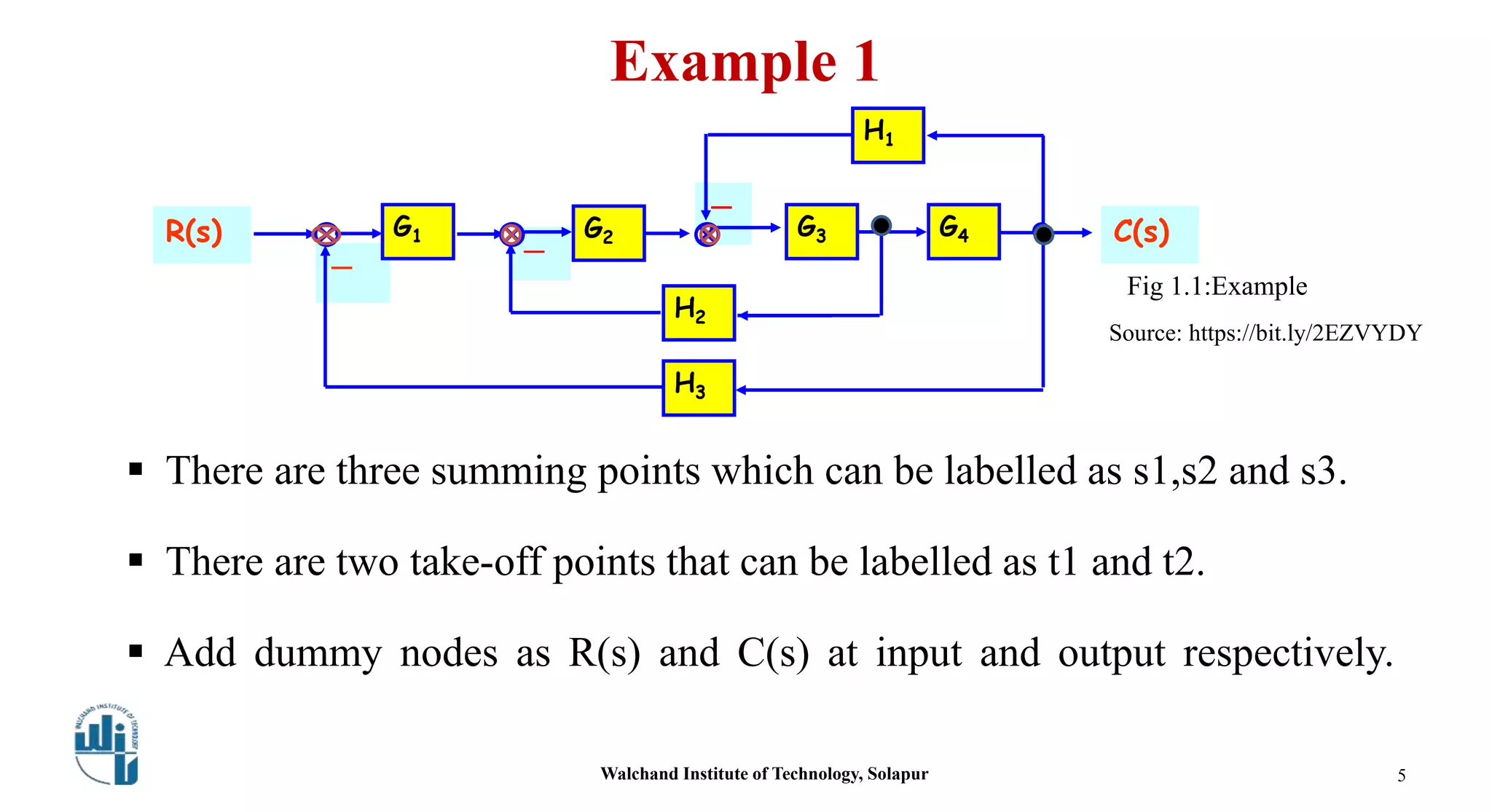
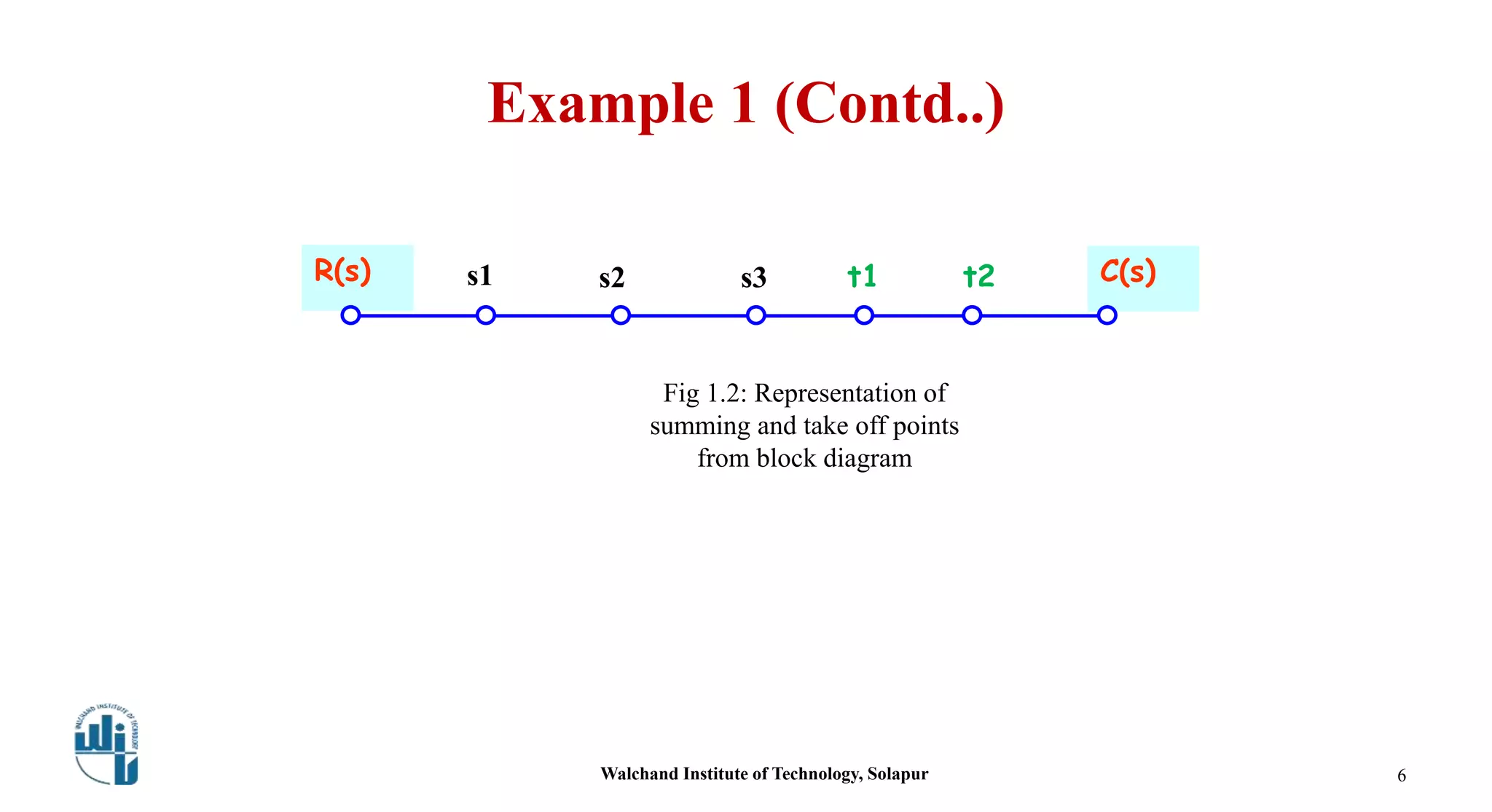
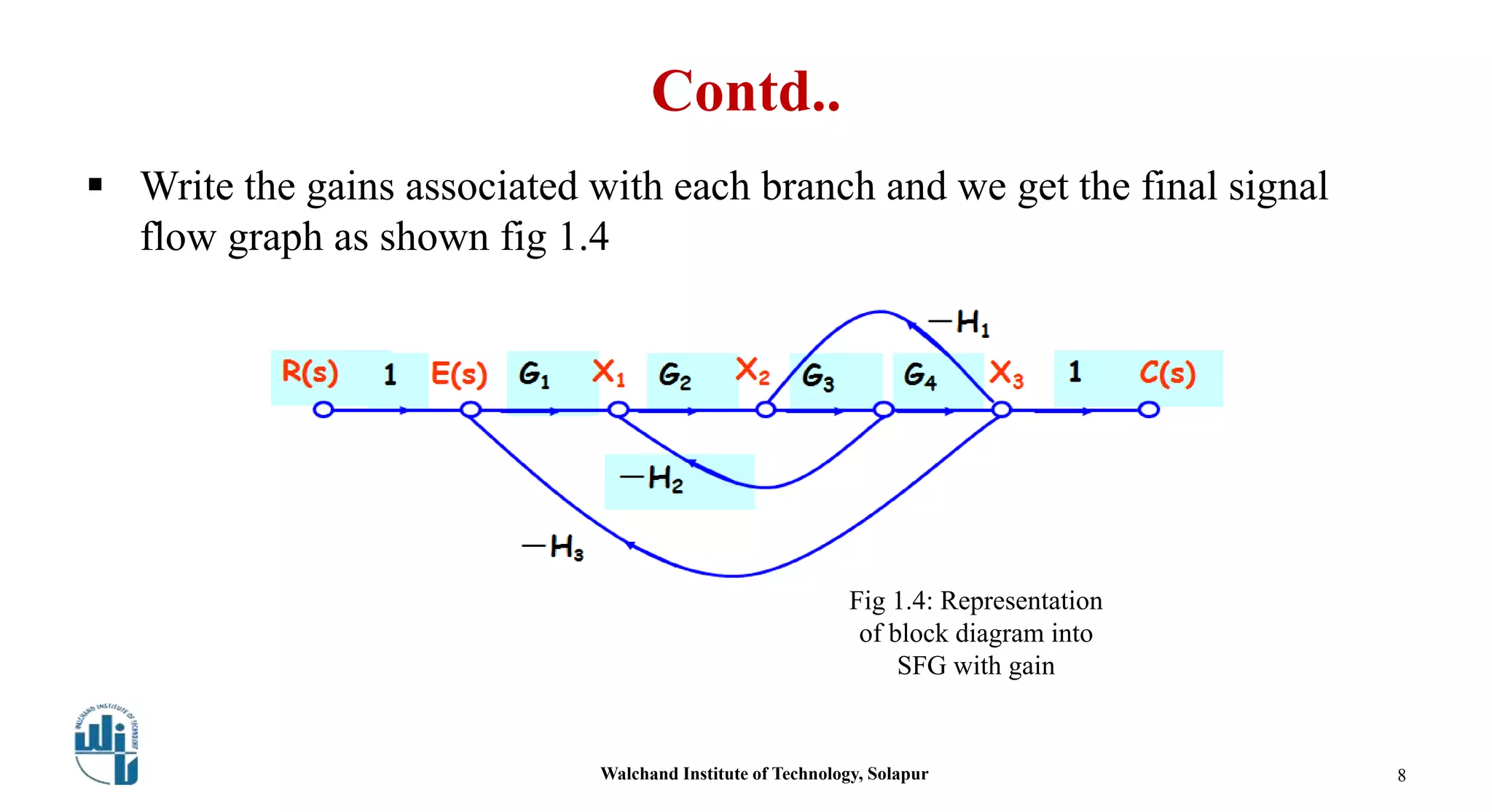
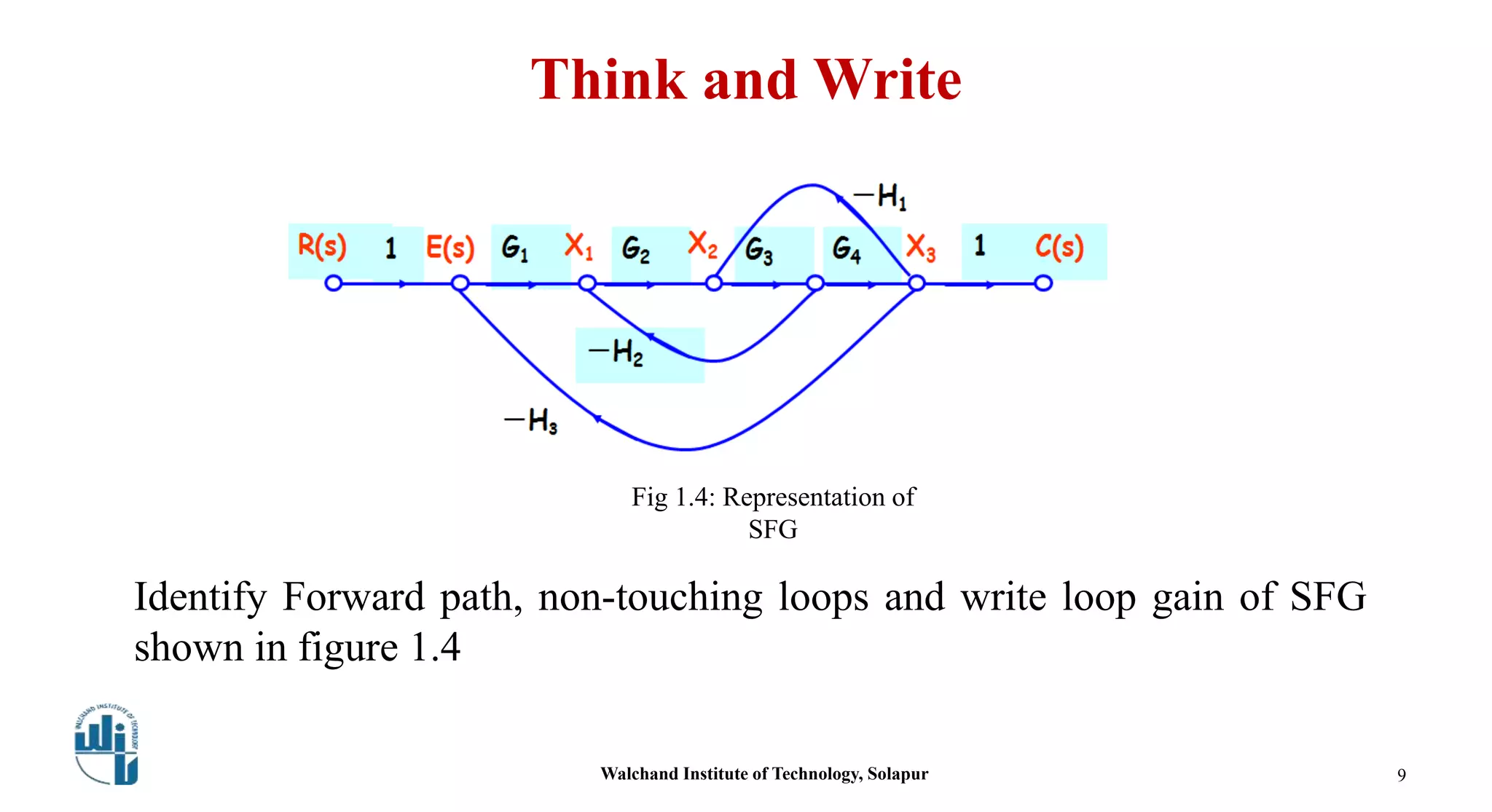
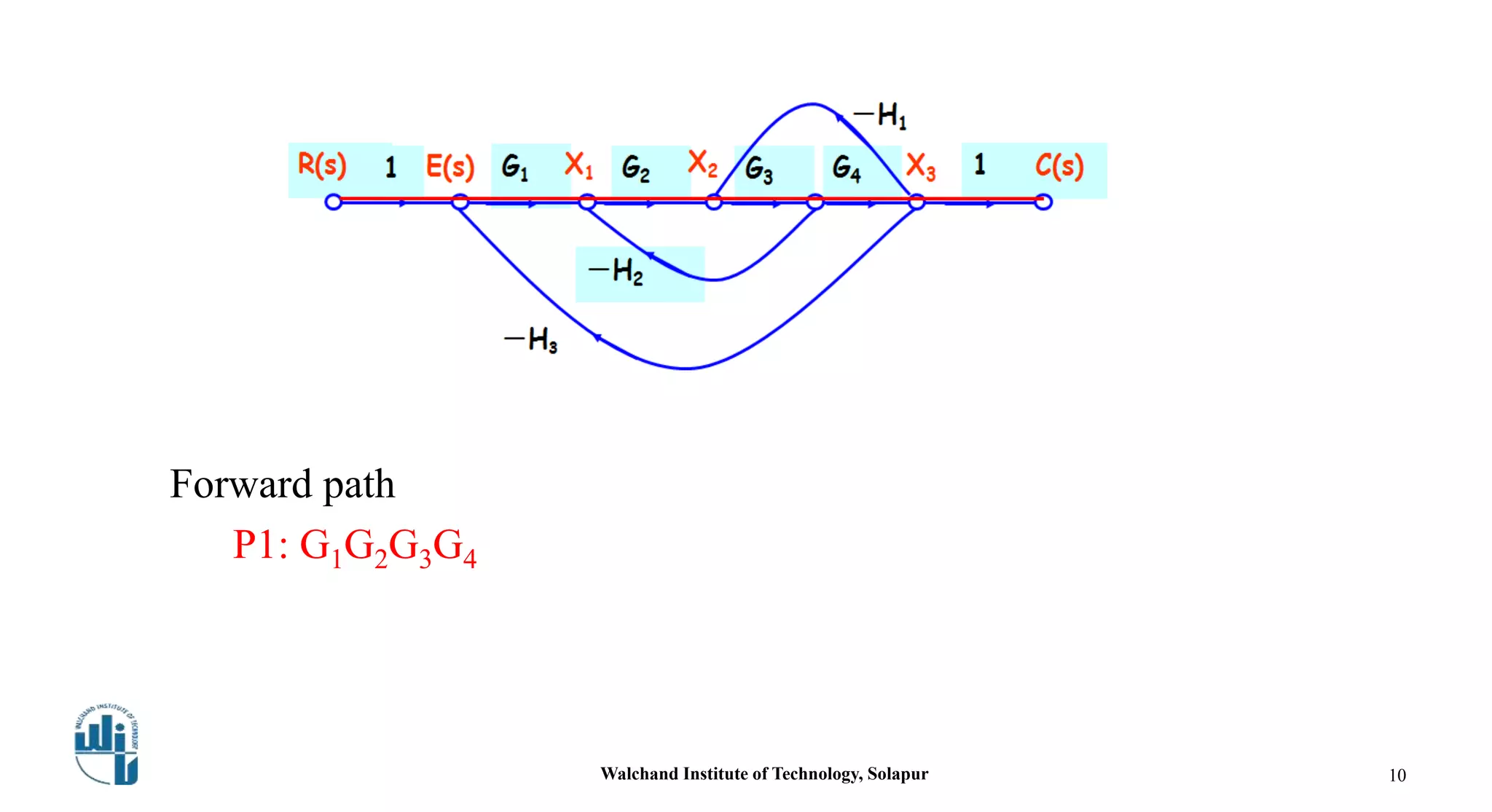
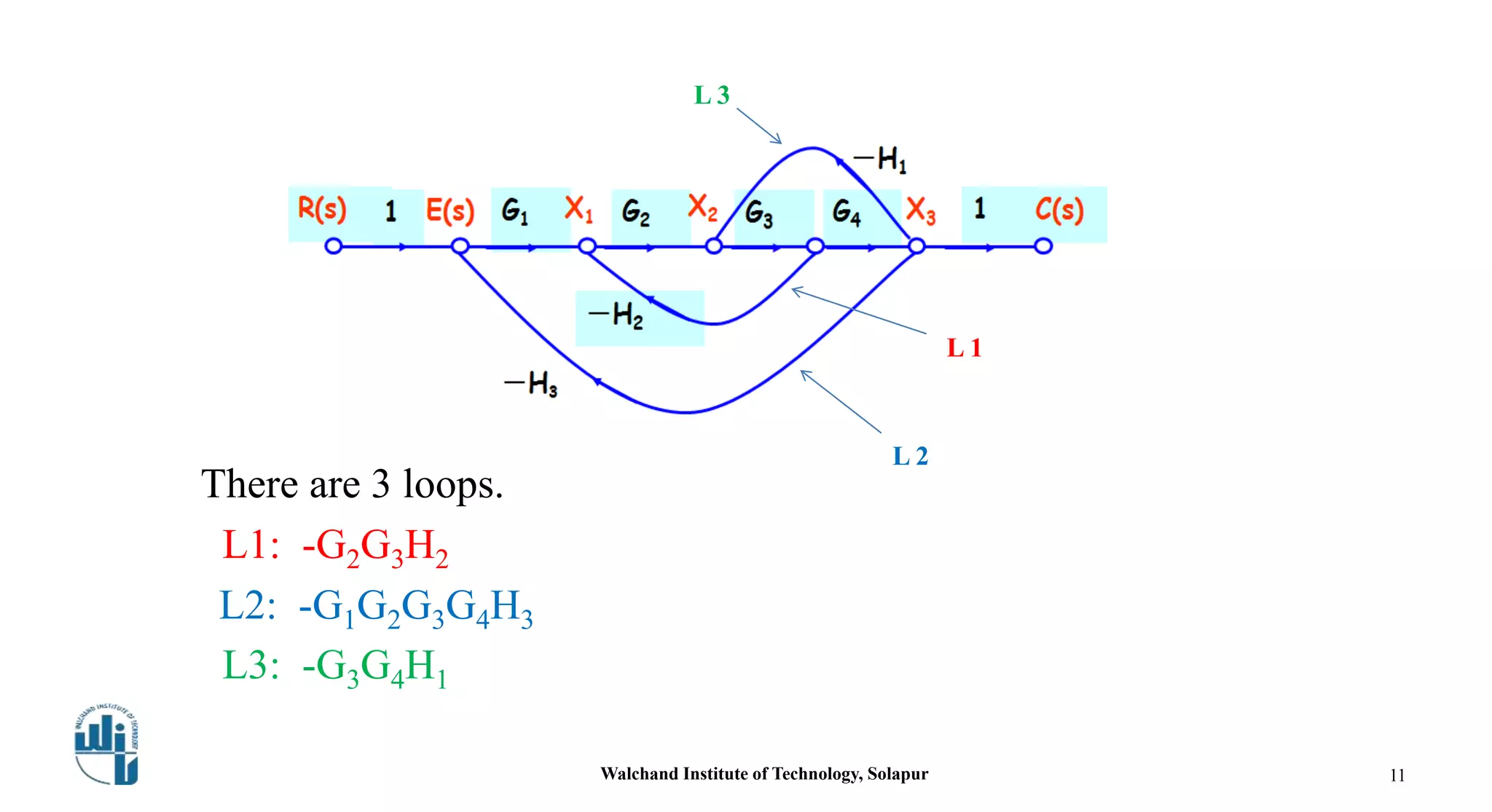
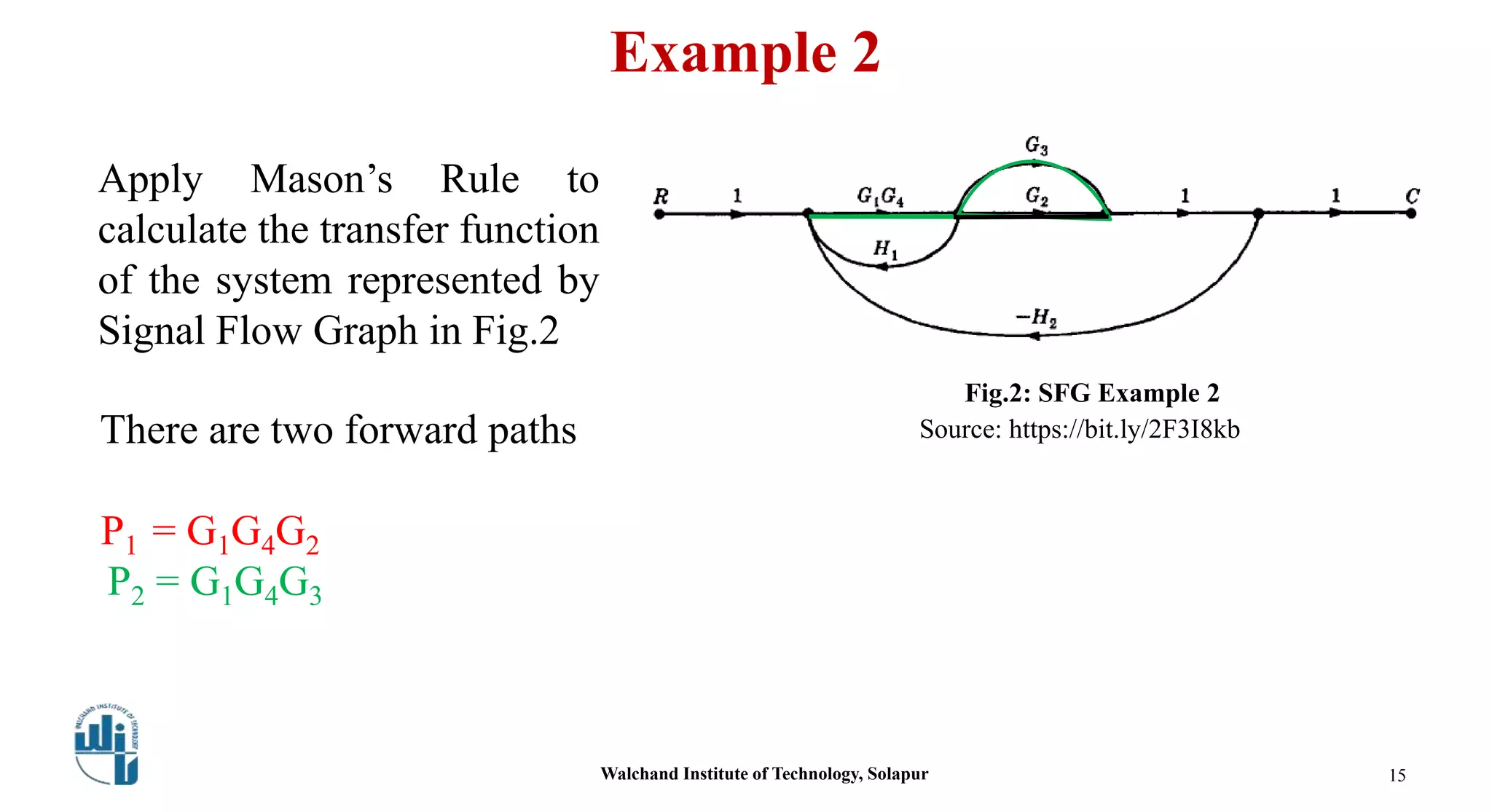
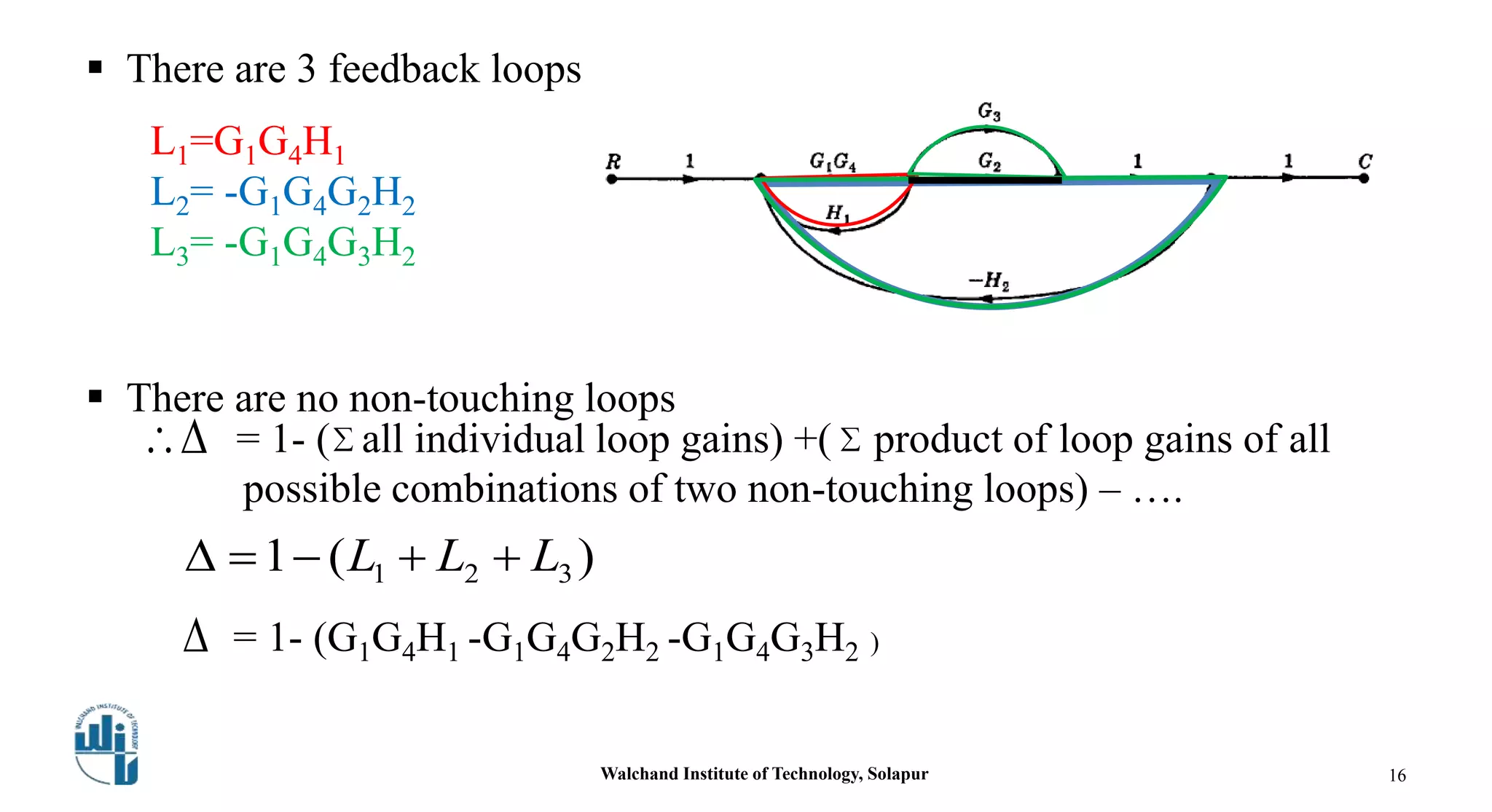
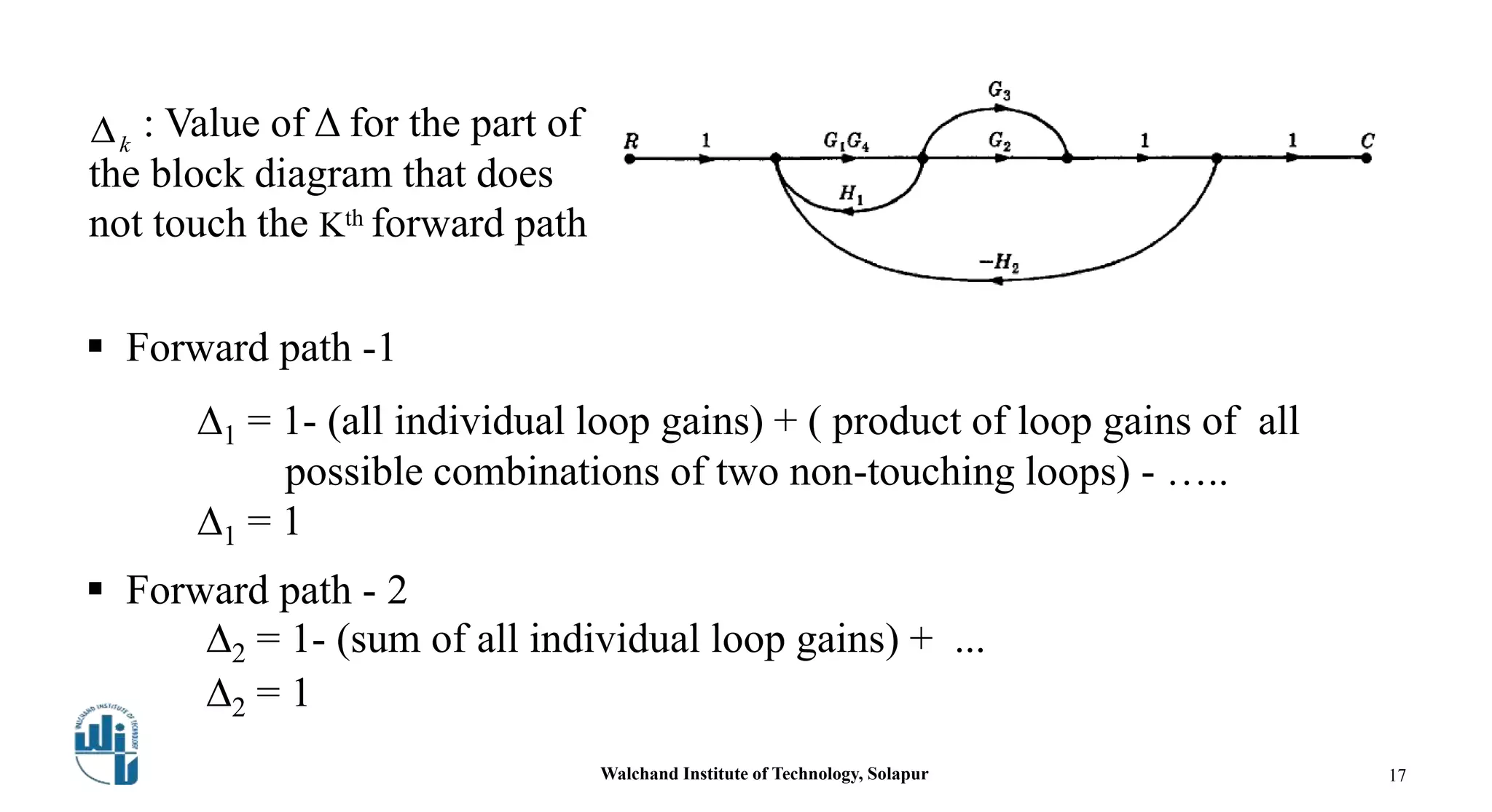
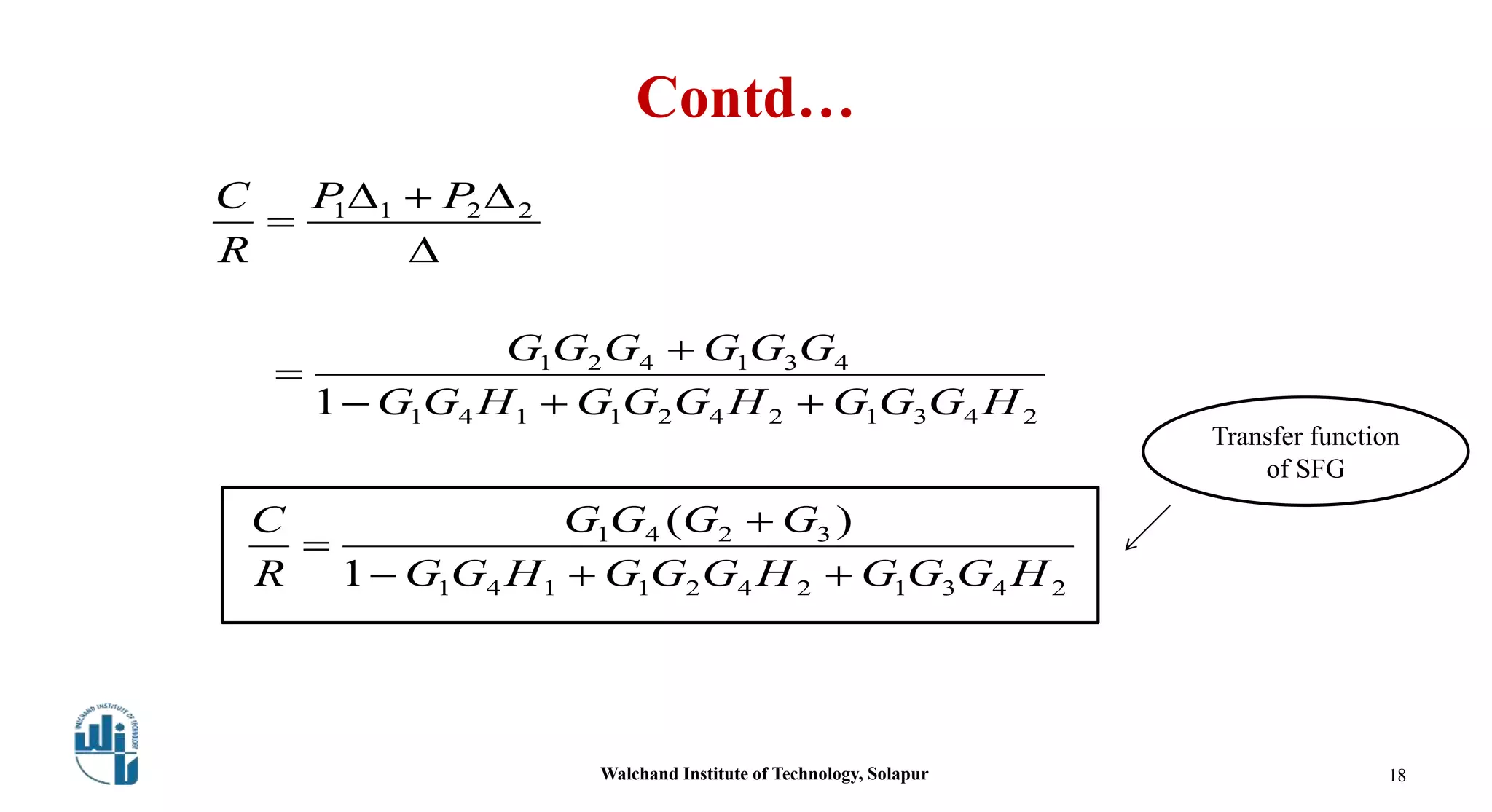
This document discusses signal flow graphs and Mason's gain formula. It begins by explaining how to convert a block diagram into an equivalent signal flow graph by labeling summing points and take-off points, assigning nodes, and connecting nodes with associated gains. An example is provided. Mason's rule for reducing a signal flow graph to a transfer function is introduced. It uses the net gain formula that considers forward paths, loop gains, and non-touching loops. Another example applies Mason's rule to calculate the transfer function. In the end, some references on the topic are listed.

1. Signal Flow Graph
and
Mason’s Gain Formula
Ms. Priyanka P. Bidla
(birla.priyanka@gmail.com)
Assistant Professor, Electronics & Telecommunication Engg.
Walchand Institute of Technology, Solapur
(www.witsolapur.org)

2. Learning Outcome
Students will be able to
1. Represent block diagram by its equivalent signal flow graph.
2. Use Mason’s rule for reducing a signal-flow graph to a system transfer
function.
Walchand Institute of Technology, Solapur 2
At the end of this session,

3. Contents
 Procedure of Block Diagram into S.F.G. representation
 Mason’s rule
 Signal flow graph reduction examples
Walchand Institute of Technology, Solapur 3

4. Conversion of Block Diagram into S.F.G.
1. Label all the summing points and take-off points on a block diagram using
variables s1,s2… and t1,t2.. respectively.
2. Assign node to every summing point and take-off points on a block
diagram.
3. Add dummy node at input and output.
4. Connect nodes as per block diagram and write gains associated with each
branch.
Walchand Institute of Technology, Solapur 4

5. Example 1
5Walchand Institute of Technology, Solapur
－
－
－
G1 G2
H2
H1
G4G3
H3
Fig 1.1:Example
Source: https://bit.ly/2EZVYDY
 There are three summing points which can be labelled as s1,s2 and s3.
 There are two take-off points that can be labelled as t1 and t2.
 Add dummy nodes as R(s) and C(s) at input and output respectively.
R(s) C(s)

6. Example 1 (Contd..)
Walchand Institute of Technology, Solapur 6
R(s) C(s)
Fig 1.2: Representation of
summing and take off points
from block diagram
s1 s2 s3 t1 t2

7. Contd..
Walchand Institute of Technology, Solapur 7
Connect nodes as per block diagram shown in fig1
R(s) C(s)s2 s3 t2s1 t1
Fig 1.3 Conversion
of Block Diagram
into SFG
Source: https://bit.ly/2EZVYDY

8. Contd..
 Write the gains associated with each branch and we get the final signal
flow graph as shown fig 1.4
Fig 1.4: Representation
of block diagram into
SFG with gain
Walchand Institute of Technology, Solapur 8

9. Think and Write
Walchand Institute of Technology, Solapur 9
Identify Forward path, non-touching loops and write loop gain of SFG
shown in figure 1.4
Fig 1.4: Representation of
SFG

10. Forward path
P1: G1G2G3G4
Walchand Institute of Technology, Solapur 10

11. There are 3 loops.
L1: -G2G3H2
L2: -G1G2G3G4H3
L3: -G3G4H1
Walchand Institute of Technology, Solapur 11
L 1
L 2
L 3

12. Mason’s Gain Formula
 S. J. Mason formula is related with the signal-flow graph and simultaneous
equations that can be written from the graph.
 In order to arrive at the system transfer function, block diagram reduction
technique requires successive application of fundamental relationships.
 Whereas Mason’s rule for reducing a signal-flow graph to a single transfer
function requires the application of one formula.
Walchand Institute of Technology, Solapur 12

13. Mason’s gain formula
 The relationship between input and output variable of a SFG is given by
Net Gain.
 Formula is given by,
Where,
K : Number of forward path
Pk : Gain of Kth forward path.



k
kkP
FT ..
Walchand Institute of Technology, Solapur 13

14. Contd…
 : 1- ( all individual loop gains) +( product of loop gains of all possible
combinations of two non-touching loops) – ( product of loop gains of
all possible combinations of three non-touching loops) + ……
: Value of Δ for the part of the block diagram that does not touch the Kth
forward path ( = 1 if there are no non-touching loops to the Kth path.)



k
k
Walchand Institute of Technology, Solapur 14

15. Example 2
Apply Mason’s Rule to
calculate the transfer function
of the system represented by
Signal Flow Graph in Fig.2
Fig.2: SFG Example 2
There are two forward paths
P1 = G1G4G2
P2 = G1G4G3
Walchand Institute of Technology, Solapur 15
Source: https://bit.ly/2F3I8kb

16.  There are 3 feedback loops
 There are no non-touching loops
Walchand Institute of Technology, Solapur 16
L1=G1G4H1
L2= -G1G4G2H2
L3= -G1G4G3H2
)(1 321 LLL 

= 1- ( all individual loop gains) +( product of loop gains of all
possible combinations of two non-touching loops) – ….

= 1- (G1G4H1 -G1G4G2H2 -G1G4G3H2 )


17.  Forward path -1
 Forward path - 2
Walchand Institute of Technology, Solapur 17
∆1 = 1- (all individual loop gains) + ( product of loop gains of all
possible combinations of two non-touching loops) - …..
∆1 = 1
∆2 = 1- (sum of all individual loop gains) + ...
∆2 = 1
k : Value of Δ for the part of
the block diagram that does
not touch the Kth forward path

18. Contd…


 2211 PP
R
C
24312421141
431421
1 HGGGHGGGHGG
GGGGGG



24312421141
3241
1
)(
HGGGHGGGHGG
GGGG
R
C



Walchand Institute of Technology, Solapur 18
Transfer function
of SFG

19. References
1] Control Systems Engineering I. J. Nagrath & M Gopal New Age
International Publication(5th Edition)
2] https://bit.ly/2EZVYDY
3] https://bit.ly/2F3I8kb
4] http://electricalacademia.com/control-systems/signal-flow-graphs-and
masons-gain-formula/
19Walchand Institute of Technology, Solapur

20. Thank you
Walchand Institute of Technology, Solapur 20