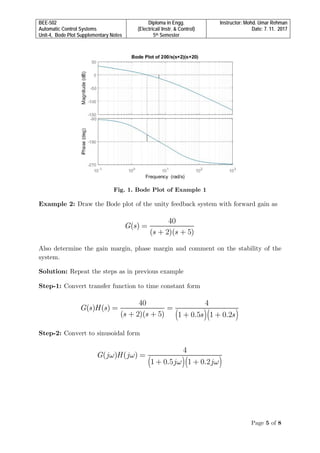
The document consists of comprehensive notes on Bode plots for automatic control systems, including methods for analyzing gain and phase margins. It provides step-by-step examples to plot Bode diagrams for various system transfer functions and determine stability conditions. The material is aimed at electrical and instrumental engineering students in their fifth semester, guided by instructor Mohd. Umar Rehman.

1. BEE-502
Automati
Unit-4, B
Determ
At ver
all oth
initial s
much l
Magnit
Compa
that th
Now, w
(i) T
T
an
(ii) T
c Control Syst
Bode Plot Supp
mination
y low freq
er terms h
slope is on
lower than
tude in dB
log G20
aring this e
he slope is
we consider
Type - 0 S
Thus, initia
nd initial m
Type - 1 S
tems
plementary No
of Initial
quencies, th
have neglig
nly determi
the corner
is given b
( ) (G j Hω
equation w
−20n dB/d
r the cases
System: n
log G20
al part of t
magnitude
System: n
lo20
tes
(Ele
l Slope of
he type te
gible contr
ined by th
r frequenci
( )G jω
by:
( )j
M
ω =
= −
20
with the eq
dec.
for variou
n = 0
( ) (G j H jω
the Bode p
is 20 log K
n = 1
( )og G j Hω
Diploma in E
ectrical/ Instr.
5th Semes
f Bode Pl
rm / (jω1
ribution to
is term, an
ies can be a
) ( )H jω ≈
( )
log
log
n
K
j
n
ω
ω
0
20
quation of
us system 't
)jω =
=
20
20
plot of a ty
K.
( )H jω =
=
Engg.
& Control)
ster
ot
)n
ω domina
wards the
nd the tran
approxima
( )
n
K
jω
≈
log
log
n
K
=
+
20
20
straight lin
types'.
( )
log
log
K
j
K
ω
0
ype - 0 sy
(
log
log
K
j
K
ω
20
20
syst
Instru
ates over a
gain mag
nsfer funct
ated as:
gK n
K
− 20
ne y = mx
log= 20
stem has a
)
log
K
ω
ω− 20
tem
uctor: Mohd. U
Date
Pag
all other te
nitude, he
ion at freq
log( )n ω
x + c, we
g
K
1
a slope 0 d
ω
Umar Rehman
e: 7. 11. 2017
ge 1 of 8
erms as
nce the
quencies
can say
dB/dec,

2. BEE-502
Automati
Unit-4, B
T
in
eq
(iii) T
T
in
eq
c Control Syst
Bode Plot Supp
The initial
ntersection
quation to
Type - 2 S
The initial p
ntersection
quation to
tems
plementary No
part of th
with the
zero.
System: n
log20
part of the
with the
zero.
tes
(Ele
he Bode p
0 dB axis
logK
ω
0
20
n = 2
( )g G j Hω
e Bode plot
0 dB axis
logK
ω
ω
2
0
20
Diploma in E
ectrical/ Instr.
5th Semes
plot has a
s can be f
log
logK
Kω
=
=
=
0 20
20
( )H jω =
=
t has a slop
s can be f
log
logK
K
Kω
=
=
=
=
2
0 20
20
Engg.
& Control)
ster
slope of
found by e
g lo
g
K
ω
− 20
(
log
log
K
j
K
ω
−
20
20
pe of −40
found by e
g lo
g
K
ω
−
2
20
Instru
−20 dB/d
equating th
og ω
)
log
K
ω
ω−
2
20
dB/dec. A
equating th
og ω
uctor: Mohd. U
Date
Pag
dec, The p
he RHS o
ω2
Again, the p
he RHS o
Umar Rehman
e: 7. 11. 2017
ge 2 of 8
point of
f above
point of
f above

3. BEE-502
Automatic Control Systems
Unit-4, Bode Plot Supplementary Notes
Diploma in Engg.
(Electrical/ Instr. & Control)
5th Semester
Instructor: Mohd. Umar Rehman
Date: 7. 11. 2017
Page 3 of 8
Let us see some examples on Bode plot.
Example 1: Draw the Bode plot of the unity feedback system with forward gain as
(
(
)
)
)(s s s
G s =
+ +
200
2 20
Also determine the gain margin, phase margin and comment on the stability of the
system.
Solution: Step-1: First convert the given transfer function into time constant form
( )( )
( ) (
)( )
.
)
(
.
s s
G s H
s
s
s
s s
s
s s
=
⎛ ⎞⎛ ⎞+ + ⎟ ⎟⎜ ⎜⎟ ⎟× × + +⎜ ⎜⎟ ⎟⎜ ⎜⎟ ⎟⎜ ⎜⎝ ⎠⎝ ⎠
=
=
+ +
200 200
2 20
2 20 1 1
2 20
5
1 0 5 1 0 05
Step-2: Determine the sinusoidal transfer function
( )( )
( ) ( )
. .
G j H j
j j j
ω ω
ω ω ω
=
+ +
5
1 0 5 1 0 05
Step-3: Identify different parts of the Bode plot
(i) Constant term: K = 5
(ii) Type of system: 1, this means initial slope is −20 dB/dec, and intersection of
the initial part of the plot with 0 dB axis occurs at rad/sKω = = 5 .
(iii) Corner frequencies: c1 c2
rad/s, rad/s
. .
ω ω= = = =
1 1
2 20
0 5 0 05
Step-4: Draw reference slopes on top left corner of the semi-log graph paper. For
magnitude plot draw a 0 dB axis line, with positive values above it like 20 dB, 40 dB
etc. and negative values below it like −20 dB, 40 dB etc. For phase plot, draw a
−180° axis line. Above it the values will be like −150°, −120°, −90° etc. and the
values below it will be like −210°, −240°, −270° etc.

4. BEE-502
Automatic Control Systems
Unit-4, Bode Plot Supplementary Notes
Diploma in Engg.
(Electrical/ Instr. & Control)
5th Semester
Instructor: Mohd. Umar Rehman
Date: 7. 11. 2017
Page 4 of 8
Step-5: Start plotting the magnitude plot by drawing a line with initial slope of
−20 dB/dec that intersects the 0 dB axis at 5 rad/s. This slope continues till first
corner frequency of 2 rad/s. Since this corner frequency is due to a pole, an
additional slope of −20 dB/dec will be added, hence the slope now will be
−40 dB/dec. This slope will continue till second corner frequency of 20 rad/s. Since
the second corner frequency is also due to a pole, an additional slope of −20 dB/dec
will be added, and hence the slope now will be −60 dB/dec. This slope will continue
for all the further values of ω.
Step-6: Phase calculation: Only denominator terms will contribute to phase angle.
The expression for phase angle is given by:
tan( ) ( ) ( . ) (tan . )G j H j ω ωφ ω ω − −
∠ = − −= −1 1
90 0 5 0 05
Using this expression, we tabulate some values of ϕ w. r. t. ω as follows:
ω 0.1 1 2 10 20 40 ∞
φ −93.15° −119.42° −140.7° −195.29° −219.28° −240.58° −270°
Step-7: Determine the value of frequency at which the magnitude plot crosses the 0
dB axis. This value is the gain crossover frequency gc
ω . Drop a perpendicular line at
this value of frequency on the phase plot and read the phase angle value. Here,
gc
. rad/sω = 2 85 and phase angle at this value is ( )gc
φ ω = − °153 .
Next, determine the value of frequency at which the magnitude plot crosses the
−180° axis. This frequency is the phase crossover frequency pc
ω . Drop a
perpendicular line at pc
ω on the magnitude plot and read the corresponding value of
magnitude. Here pc
. rad/sω = 6 3 and magnitude is ( )pc
M ω = −13 dB.
Step-8: Calculate the stability margins
Gain Margin, ( )pc
( )GM M ω= − = − − = +0 0 13 13 dB.
Phase Margin, ( )gc
( )PM φ ω= + = + − ° = °180 180 153 27
Since both the margins are positive, the system is stable.
A Bode plot drawn by software is shown here and all values given here are for
reference only. The closer your values are to these values, the more accurate your
Bode plot will be.

5. BEE-502
Automatic Control Systems
Unit-4, Bode Plot Supplementary Notes
Diploma in Engg.
(Electrical/ Instr. & Control)
5th Semester
Instructor: Mohd. Umar Rehman
Date: 7. 11. 2017
Page 5 of 8
Fig. 1. Bode Plot of Example 1
Example 2: Draw the Bode plot of the unity feedback system with forward gain as
(
(
)
)
)(s s
G s =
+ +
40
2 5
Also determine the gain margin, phase margin and comment on the stability of the
system.
Solution: Repeat the steps as in previous example
Step-1: Convert transfer function to time constant form
( )( )
( ) (
( ) . .
)
)(s s
G s H s
s s
=
+ + +
=
+
40 4
2 5 1 0 5 1 0 2
Step-2: Convert to sinusoidal form
( )( )
( ) ( )
. .
G j H j
j j
ω ω
ω ω+ +
=
0 5 01 2
4
1

6. BEE-502
Automatic Control Systems
Unit-4, Bode Plot Supplementary Notes
Diploma in Engg.
(Electrical/ Instr. & Control)
5th Semester
Instructor: Mohd. Umar Rehman
Date: 7. 11. 2017
Page 6 of 8
Step-3: Different parts of the plot
(i) Constant term: K = 4
(ii) Type of system: 0, this means initial slope is 0 dB/dec, and initial magnitude
is 20 log K = 20 log 4 = 12.04 dB
(iii) Corner frequencies: c1 c2
rad/s, rad/s
. .
ω ω= = = =
1 1
2 5
0 5 0 2
Step-4: Draw reference slopes and axes.
Step-5: Draw magnitude plot.
Step-6: Draw phase plot, tan tan( ) ( ) ( . ) ( . )G j H jφ ω ω ω ω− −
∠= −= − 1 1
0 5 0 2
Using this expression, tabulate some values of φ w. r. t. ω as follows:
ω 0.1 1 2 5 10 20 ∞
φ −40.08° −37.87° −66.80° −113.2° −142.1° −160.25° −180°
Step-7: Gain cross-over and phase cross-over frequencies and corresponding values
of phase and magnitude.
( )
( )
gc gc
pc pc
. rad/s,
rad/s, dBM
ω φ ω
ω ω
= =
= ∞ = −∞
5 18 115
Step-8: Stability margins
Gain Margin, ( )pc
( )GM M ω= − = − −∞ = +∞0 0 dB.
Phase Margin, ( )gc
PM φ ω= + = − =180 180 115 65
The phase plot curve is asymptotic to −180° axis at high frequencies and the gain at
high crossover is negative such that the GM is +∞. Since, both PM and GM are
positive, therefore, the system is stable. Further the GM is infinite, hence, the system
is inherently stable.

7. BEE-502
Automatic Control Systems
Unit-4, Bode Plot Supplementary Notes
Diploma in Engg.
(Electrical/ Instr. & Control)
5th Semester
Instructor: Mohd. Umar Rehman
Date: 7. 11. 2017
Page 7 of 8
Fig. 2. Bode Plot of Example 2
Example 3: Determine the open loop transfer function of a system whose
magnitude Bode plot is shown below.
Fig. 2. Bode Plot of Example 3
Solution: We see that the initial slope of the magnitude Bode plot is 0 dB/dec, so it
is a type - 0 system. Also, the initial magnitude is 20 dB.
Hence, log logK K K= ⇒ = ⇒ =20 120 10
20

8. BEE-502
Automatic Control Systems
Unit-4, Bode Plot Supplementary Notes
Diploma in Engg.
(Electrical/ Instr. & Control)
5th Semester
Instructor: Mohd. Umar Rehman
Date: 7. 11. 2017
Page 8 of 8
There is one corner frequency due to pole at ω1 = 10 rad/s and another corner
frequency due to zero at ω2 = 1000 rad/s. Hence, we can write the TF as:
( )
( )
( )
( )
( )
( )
( )
s
s
s
K sT
G s
sT s
s
s
ω
ω
−
−
⎛ ⎞⎟⎜ ⎟+⎜ ⎟⎜ ⎟⎟⎜+ ⎝ ⎠
= =
⎛ ⎞+ ⎟⎜ ⎟+⎜ ⎟⎜ ⎟⎟⎜⎝ ⎠
+ +
= =
++
22
3
1
1
1
10 1
1
1
1
10 1 10 1000
10 101 10
*** End of Unit - 4 ***