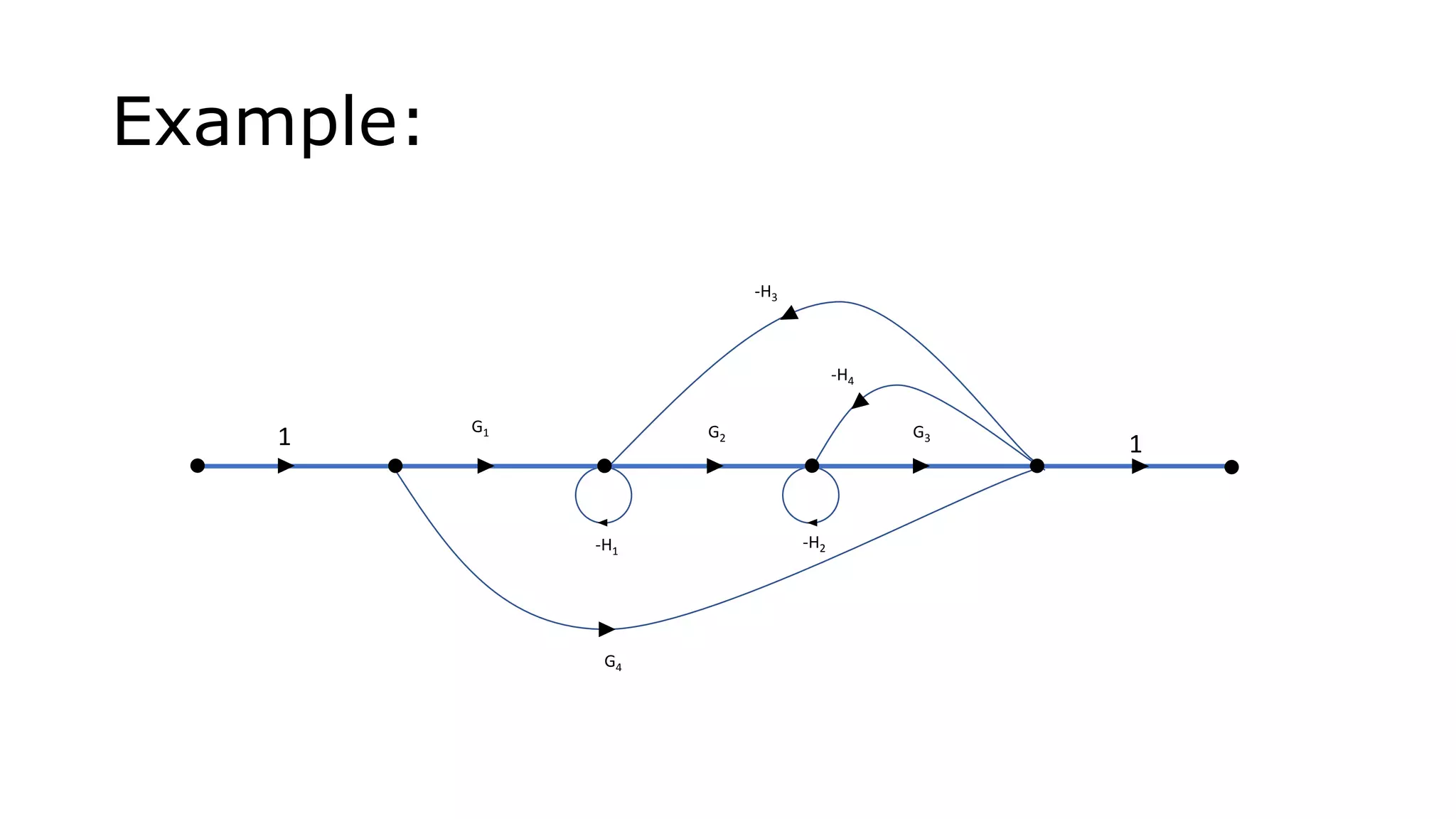
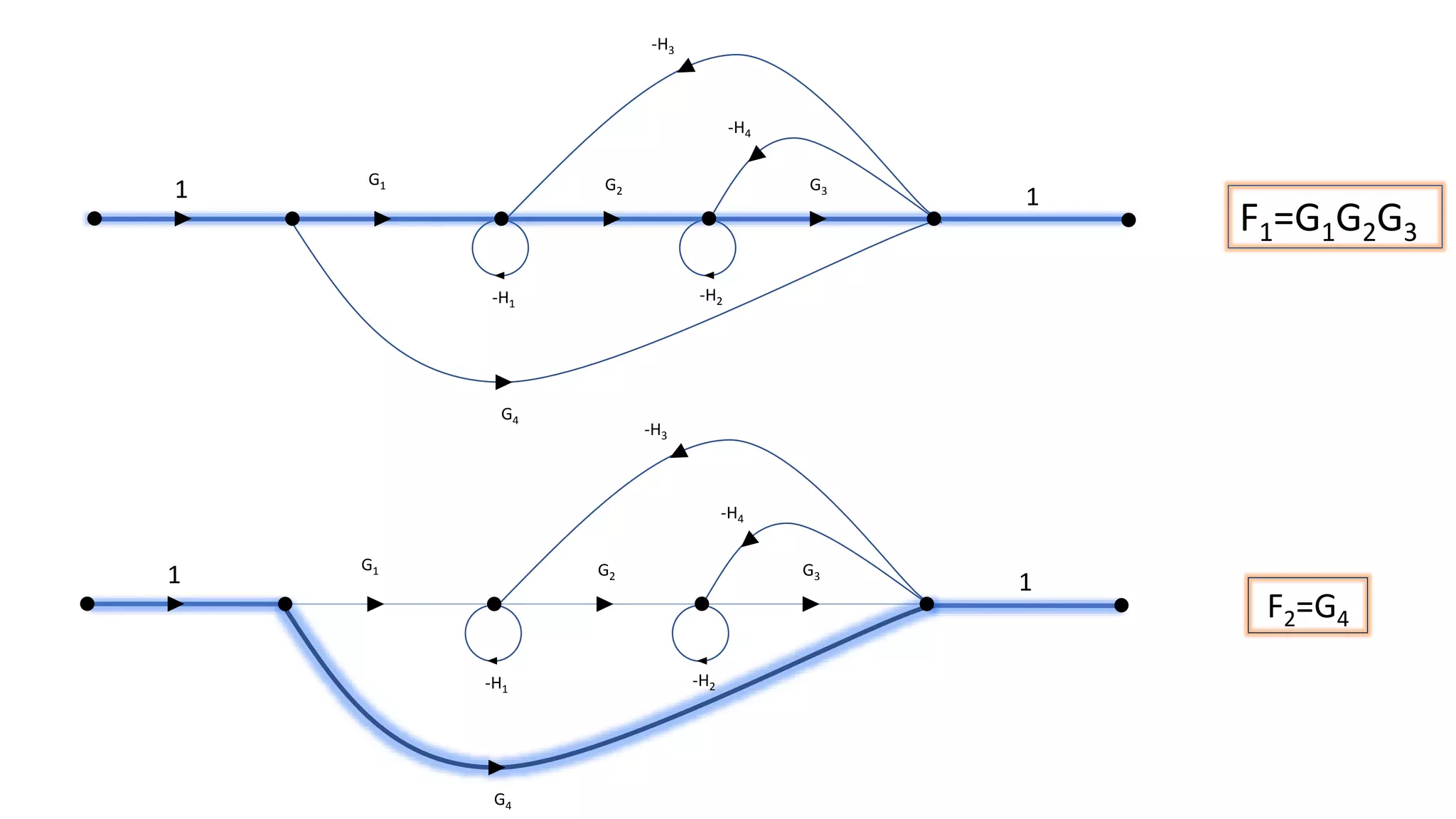
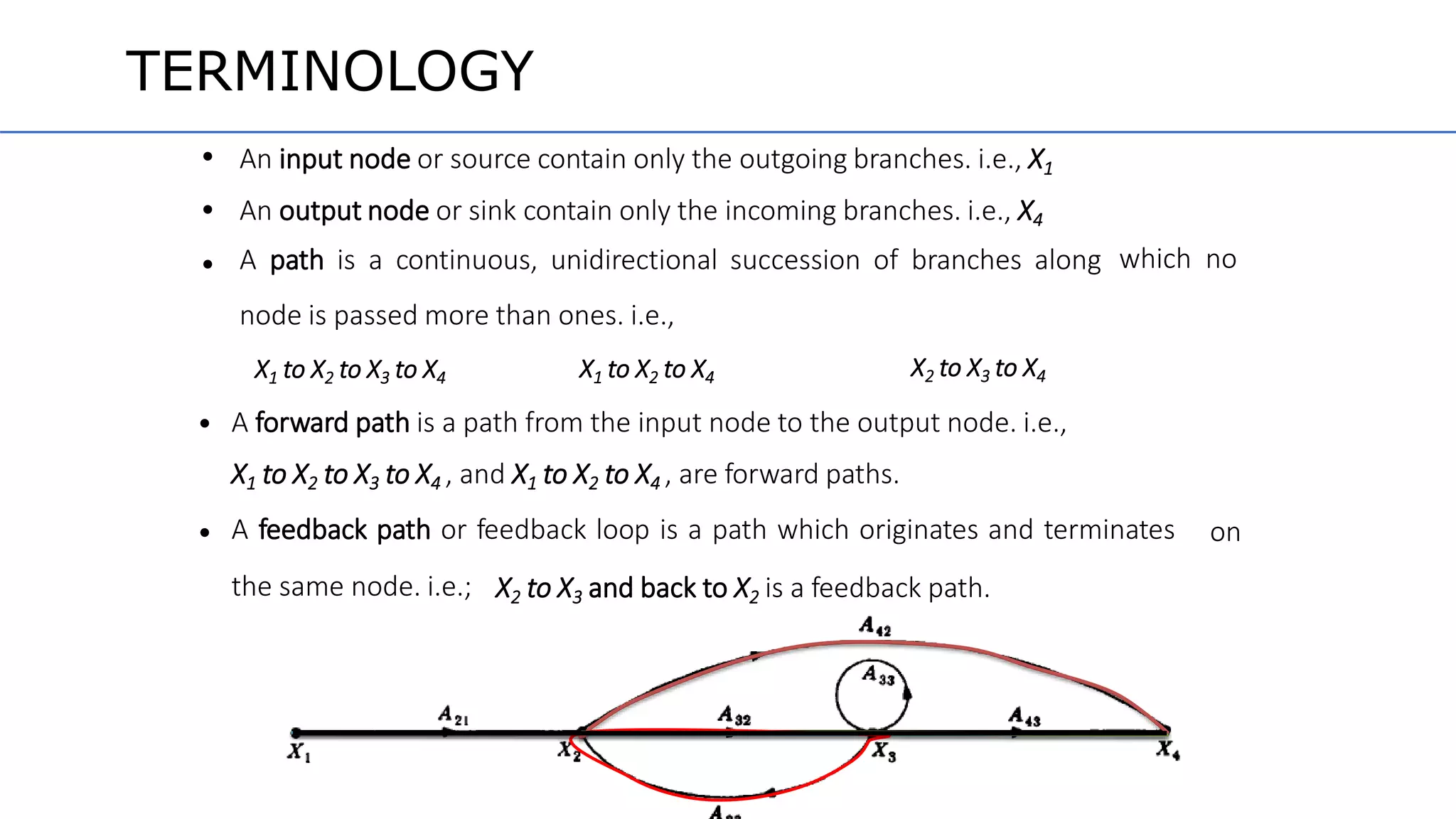
This document discusses signal flow graphs and Mason's rule for analyzing control systems. It begins with an introduction to signal flow graphs and their basic components and terminology. It then explains Mason's rule, which provides a formula for reducing a signal flow graph to a single transfer function. The formula relates the graph to the simultaneous equations that can be written from it. The document provides an example of applying Mason's rule to calculate the transfer function of a sample signal flow graph. It demonstrates identifying forward paths, calculating loop transmittances, and determining the characteristic function and path determinants.

1. SIGNAL FLOW GRAPH
CONTROL SYSTEM
(2150909)
PREET PATEL (151310109032)
Electrical Engineering Department

2. CONTENTS
• Introduction
• Fundamentals
• Terminology
• Mason’s rule
• Example

3. 3
INTRODUCTION
• A signal flow graph consists of a network in which nodes are connected by
directed branches.
• It depicts the flow of signal from one point of a system to another and gives
the relationship among the signal.

4. FUNDAMENTALS OF SIGNAL FLOW GRAPHS
• Consider a simple equation below and draw its signal flow
y  ax
graph:
• The signal flow graph of the equation is shown below;
a
yx
•
•
Every variable in a signal flow graph is designed by a Node.
Every transmission function in a signal flow graph is designed
Branch.
Branches are always unidirectional.
by a
•
• The arrow in the branch denotes the direction of the signal flow.

5. An input node or source contain only the outgoing branches. i.e., X1
An output node or sink contain only the incoming branches. i.e., X4
A path is a continuous, unidirectional succession of branches along
node is passed more than ones. i.e.,
•
•
• which no
X2 to X3 to X4X1 to X2 to X3 to X4 X1 to X2 to X4
• A forward path is a path from the input node to the output node. i.e.,
X1 to X2 to X3 to X4 , and X1 to X2 to X4 , are forward paths.
A feedback path or feedback loop is a path which originates and terminates• on
the same node. i.e.; X2 to X3 and back to X2 is a feedback path.
TERMINOLOGY

6. MASON’S RULE (MASON,
1953)
• The block diagram reduction technique requires successive
application of fundamental relationships in order to arrive at the
system transfer function.
On the other hand, Mason’s rule for reducing a signal-flow graph•
to a single transfer function requires the application of one
formula.
The formula was derived by S. J. Mason when he related the•
signal-flow graph to the simultaneous equations that can be
written from the graph.

7. Where,
n = number of forward paths.
i thPi = the forward-path gain.
ith∆i = Determinant of the forward path
∆ is called the signal flow graph determinant or characteristic function.
Since, ∆=0 is the system characteristic equation.
Pi i
C(s)
T  i1

R(s)
n
MASON’S RULE

8. ∆ = 1- (sum of all individual loop transmittance) + (sumof the products of
loop transmittance of all possible pairs of Non Touching loops) – (sum of
the products of loop transmittance of Triple of Non Touching loop) + …
∆i = Calculate ∆ for ith path
=1- [loop transmittance of single Non Touching loops with forward path]
+ [loop transmittance of pair of Non Touching loops withforward path]
MASON’S RULE

9. • Calculate forward path gain Pi for each forward path i.
• Calculate all loops transfer function.
• Consider non touching loops 2 at a time
• Consider non touching loops 3 at a time
• Calculate Δ from steps 2,3,4 and 5
• Calculate Δi as portion of Δ not touching forward path i.
SYSTEMATIC APPROACH

10. Example:
1 1
-H3
-H4
-H1
-H2
G1 G2 G3
G4

11. 1 1
-H3
-H4
-H1
-H2
G1 G2 G3
G4
1 1
-H3
-H4
-H1
-H2
G1 G2 G3
G4
F2=G4
F1=G1G2G3

12. • Obtain total number of single loop:
L11= -H1,
L21 = H2,
L31 = G3H4,
L41= G2G3H3
• Obtain total number of 2 non-touching loops:
L12= L11 and L21 = H1H2
L22 = L11 and L31 = G3H4H1
• There are no 3 non touching loops.
• Find out the value of
L11 + L21 + L31 + L41 + L12 + L22
-H1 + H2 + G3H4 + G2G3H3 + H1H2 + G3H4H1

13. • Find out value of ∆1 and ∆2
Take F1 and Find ∆1
Since all loops touch the F1 forward path, ∆1=1
Take F2 and ∆2
L 11 and L21 do not touch the forward path
∆2= 1 - (L11 + L21)
∆2= 1 + H1+ H2
• Obtain the transfer function:
𝐶(𝑠)
𝑅(𝑠)
=
𝐺1 𝐺2 𝐺3 + 𝐺4(1 + 𝐻1 + 𝐻2)
1 + H1+ H2 + G3H4 + G2G3H3 + H1H2 + G3H4H1

14. THANK YOU
14