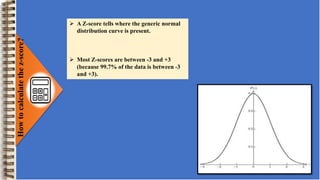
A z-score is a measurement that describes a value's relationship to the mean of a group of values. It is measured in standard deviations from the mean. A z-score of 0 indicates the value is identical to the mean. Z-scores are useful for standardizing values in a normal distribution and comparing them. Examples show how to calculate z-scores and use them to compare test scores from different distributions and determine statistical significance between sample means. Z-scores are also used to find probabilities for values occurring in a normal distribution.

1. Z-SCORE

2. INTRODUCTION
A Z-score is a numerical measurement that
describes a value's relationship to the mean of a
group of values.
Z-score is measured in terms of standard deviations
from the mean.
If a Z-score is 0, it indicates that the data point's
score is identical to the mean score.

3. How
to
calculate
the
z-score?  A Z-score tells where the generic normal
distribution curve is present.
 Most Z-scores are between -3 and +3
(because 99.7% of the data is between -3
and +3).

4. FORMULA
OF
Z-SCORE
 For Two - Sample Where,
x
̄ 1 = Mean of the First Sample
x
̄ 2 = Mean of the Second Sample
μ1 = Mean of the First
Population
μ2 = Mean of the Second
Population
(μ1 – μ2) = Hypothesized
Difference Between the
Population Means
σ1 = Standard Deviation of the
First Population
σ2 = Standard Deviation of the
Second Population
 For Standard Error of the Mean
Where,
“x” = Raw Score,
“µ” = Population Mean,
“σ” = Standard Deviation
“n” = Number of Observations
 For One - Sample
z =
x - µ
σ
Where,
“x” =Raw Score,
“µ”=Population Mean,
“σ”=Standard Deviation
Formula
of
Z-Score

5. How
to
interpret
a
z-score?
How
to
interpret
a
Z-Score?

6. HOW
TO
CALCULATE
THE
P-
VALUE
FROM
Z-TABLE?
Z = 2.00
Z = 1.06
Z = 0.48
Z = 2.94
How
to
calculate
P-Value
from
Z-Score?

7. How
to
interpret
Z
–
Score
in
Python?
How
to
interpret
Z-Score
in
Python?
Z score = 0.35406698564593303
RUN
import statistics
Sample_Mean = 1100
Population_Mean = 1026
Stdev = 209
Z=(Sample_Mean-Population_Mean)/Stdev
print("Z score =",Z)

8. How
to
interpret
Z
–
Score
in
Python?
How
to
interpret
Z-Score
in
Python?
Data : [1, 8, 9, 7, 6, 5, 4, 3, 7, 8]
Mean: 5.8
Standard Deviation : 2.5298221281347035
Zscore : [-2. 0.91666667 1.33333333 0.5 0.08333333
-0.33333333
-0.75 -1.16666667 0.5 0.91666667]
RUN
import statistics
import scipy.stats as stats
A = [1,8,9,7,6,5,4,3,7,8]
print ("Data :",A)
mean = statistics.mean(A)
print ("nMean:", mean)
stdev = statistics.stdev(A)
print ("nStandard Deviation :",stdev)
zscore = stats.zscore(A)
print ("nZscore :", zscore)

9. How
to
interpret
Z-Score
in
R
Studio?
a <- c(9, 10, 12, 14, 5, 8, 9)
mean(a)
sd(a)
a.z_score <- (a - mean(a)) / sd(a)
plot(a.z_score, type="o", col="green")
> a <- c(9, 10, 12, 14, 5, 8, 9)
> mean(a)
[1] 9.571429
> sd(a)
[1] 2.878492
> a.z_score <- (a - mean(a)) / sd(a)
> plot(a.z_score, type="o", col="green")
RUN

10. Why
is
z-score
important?
It is useful to standardize the values (raw scores) of a normal distribution by
converting them into z-scores because:
Importance

11. Example
1
 Suppose SAT scores among college students are normally distributed
with a mean of 500 and a standard deviation of 100.If a student scores
a 700,what would be her z-score?
Z-score = Where,
x = 700, µ = 500, σ = 100
=2
 Her z-score would be 2 which means her score is two standard
deviations above the mean.
700 - 500
100
Example
1

12. Example
2
 A set of Math test scores has a mean of 70 and a standard deviation of 8.
And a set of English test scores has a mean of 74 and a standard deviation of 16.
For which test would a score of 78 have a higher standing?
Find the z-score for each test:
z-score of Math Test= =1
z-score of English Test= =0.25
 The Math score would have the highest standing since it is 1
standard deviation above the mean while the English score is
only 0.25 standard deviation above the mean.
78-70
8
78 - 74
16
Example
2

13. Example
3
 A company wanted to compare the performance of its call center employees in two
different centers located in two different parts of the country – Hyderabad, and
Bengaluru, in terms of the number of tickets resolved in a day (hypothetically
speaking). The company randomly selected 30 employees from the call center in
Hyderabad and 30 employees from the call center in Bengaluru. Calculate the P-Value.
Hyderabad: x
̄ 1 = 750, σ1 = 20
Bengaluru: x
̄ 2 = 780, σ2 = 25
First, we will formulate the null and alternate hypotheses and set the level of significance for the test.
H0: There is no difference between the performance of employees at different call centers.
H1: There is a difference in the performance of the employees.
The level of significance is set as 0.05.
Next, the mean and standard deviation for each sample will need to be determined.
Hyderabad: x
̄ 1 = 750, σ1 = 20
Bengaluru: x
̄ 2 = 780, σ2 = 25
Next, we will calculate the hypothesized difference between the two population means.
In this case, the company is hypothesizing that the mean performance in Hyderabad is the same as that of
Bengaluru. So, (μ1 – μ2 ) = 0
Finally, we will use the formula for two-sample z-test for means to calculate the test statistic.
z= (x
̄ 1 – x
̄ 2 ) / √((σ1 )²/n1 + (σ2)²/n2)
z = (-30) / √((20)²/30 + (25)²/30))
z = -5.13
 At a significance level of 0.05, the p-value is less than 0.00001. As the p-value is lot less than the critical
value of 0.05, the result is statistically significant and hence you can reject the null hypothesis. Hence,
the performance of Hyderabad’s team is considered to be not equal to the performance of Bengaluru’s
team.

14. Example
3
 In general, the mean height of women is 65″ with a standard deviation of
3.5″. What is the probability of finding a random sample of 50 women with
a mean height of 70″, assuming the heights are normally distributed?
z = (x – μ) / (σ / √n)
= (70 – 65) / (3.5/√50) = 5 / 0.495 = 10.1
 The key here is that we’re dealing with a sampling distribution of
means, so we know we have to include the standard error in the
formula. We also know that 99% of values fall within 3 standard
deviations from the mean in a normal probability distribution
(see 68 95 99.7 rule). Therefore, there’s less than 1% probability
that any sample of women will have a mean height of 70″.