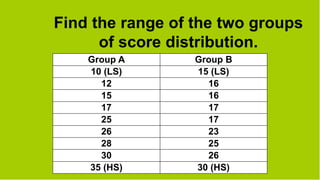
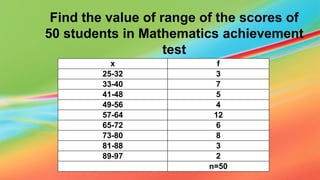
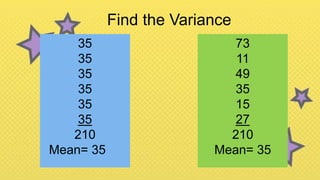
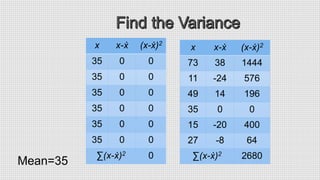
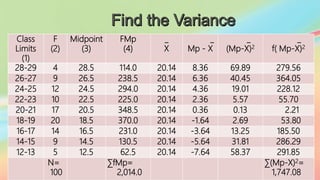
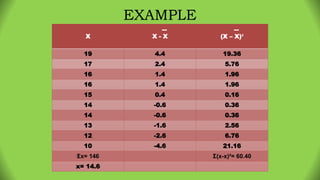
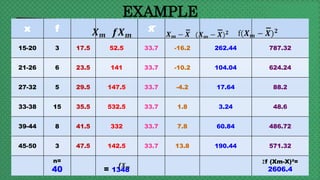
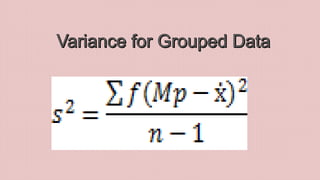The document discusses various statistical concepts including range, mean deviation, variance, and standard deviation. It provides formulas and steps to calculate each measure. The range is the distance between the highest and lowest values. Mean deviation measures the average deviation from the mean. Variance is the average of the squared deviations from the mean and standard deviation is the square root of the variance, representing the average distance from the mean. Examples are given to demonstrate calculating each measure for both ungrouped and grouped data.

5. Importance
of Range
Tells you
the
distance
from the
smallest to
largest.

6. Ungrouped Data
R= HS-LS
Whereas:
R- Range
HS- Highest score
LS- Lowest score

7. Find the range of the two groups
of score distribution.
Group A Group B
10 (LS) 15 (LS)
12 16
15 16
17 17
25 17
26 23
28 25
30 26
35 (HS) 30 (HS)

8. Group A
RA= HS-
LS
RA =35-10
RA =25
Group B
RB= HS-LS
RB= 30-15
RB= 15

9. Grouped Data
R= HSUB-LSLB
Whereas:
R- Range
HSUB – Upper boundary of highest
score
LSLB – Lower boundary of lowest
score

10. Find the value of range of the scores of
50 students in Mathematics achievement
test
x f
25-32 3
33-40 7
41-48 5
49-56 4
57-64 12
65-72 6
73-80 8
81-88 3
89-97 2
n=50

11. LS= 25
LSLB= 24.5
HS= 97
HSUB= 97.5
R= HSUB-LSLB
R=97.5-24.5
R= 73

12. end

15. Mean Deviation
Measures the average deviation of the
values from the arithmetic mean. It
gives equal weight to the deviation of
every score in the distribution.

16. A. Mean Deviation for Ungrouped Data
MD =
Where,
MD = mean deviation value
X = individual score
= sample mean
N = number of cases

17. Steps in Solving Mean Deviation for
Ungrouped Data
1. Solve the mean value.
2. Subtract the mean value from each
score.
3. Take the absolute value of the
difference in step 2.
4. Solve the mean deviation using the
formula MD =

18. Example 1: Find the mean
deviation of the scores of
10 students in a
Mathematics test. Given
the scores: 35, 30, 26, 24,
20, 18, 18, 16, 15, 10

20. Analysis:
The mean deviation of the
10 scores of students is
6.04. This means that on the
average, the value deviated
from the mean of 212 is
6.04.

22. 1. Solve for the value of the mean.
2. Subtract the mean value from each midpoint or class mark.
3. Take the absolute value of each difference.
4. Multiply the absolute value and the corresponding class
frequency.
5. Find the sum of the result in step 4.
6. Solve for the mean deviation using the formula for grouped
data.

23. Example 2: Find the mean deviation of
the given below.

24. Analysis:
The mean deviation of the
40 scores of students is
0.63. This means that on
the average, the value
deviated from the mean
of 33.63 is 10.63.

26.  is the square of the standard deviation.
In short, having obtained the value of the
standard deviation, you can already
determine the value of the variance.

27. One of the most important
measures of variation.It
shows variation at the
mean.

29. How to Calculate the Variance
for Ungrouped Data
1. Find the Mean.
2. Calculate the difference between
each score and the mean.
3. Square the difference between
each score and the mean.

30. How to Calculate the Variance
for Ungrouped Data
4. Add up all the squares of the
difference between each score
and the mean.
5. Divide the obtained sum by n – 1.

31. Find the Variance
35
35
35
35
35
35
210
Mean= 35
73
11
49
35
15
27
210
Mean= 35

32. x x-ẋ (x-ẋ)2
35 0 0
35 0 0
35 0 0
35 0 0
35 0 0
35 0 0
∑(x-ẋ)2 0
x x-ẋ (x-ẋ)2
73 38 1444
11 -24 576
49 14 196
35 0 0
15 -20 400
27 -8 64
∑(x-ẋ)2 2680
x x-ẋ (x-ẋ)2
35 0 0
35 0 0
35 0 0
35 0 0
35 0 0
35 0 0
∑(x-ẋ)2 0
Mean=35

35. 1. Calculate the mean.
2. Get the deviations by finding the
difference of each midpoint from the
mean.
3. Square the deviations and find its
summation.
4. Substitute in the formula.

36. Class
Limits
(1)
F
(2)
Midpoint
(3)
FMp
(4)
_
X
_
Mp - X
_
(Mp-X)2
_
f( Mp-X)2
28-29 4 28.5 114.0 20.14 8.36 69.89 279.56
26-27 9 26.5 238.5 20.14 6.36 40.45 364.05
24-25 12 24.5 294.0 20.14 4.36 19.01 228.12
22-23 10 22.5 225.0 20.14 2.36 5.57 55.70
20-21 17 20.5 348.5 20.14 0.36 0.13 2.21
18-19 20 18.5 370.0 20.14 -1.64 2.69 53.80
16-17 14 16.5 231.0 20.14 -3.64 13.25 185.50
14-15 9 14.5 130.5 20.14 -5.64 31.81 286.29
12-13 5 12.5 62.5 20.14 -7.64 58.37 291.85
N=
100
∑fMp=
2,014.0
∑(Mp-X)2=
1,747.08

39. TANDARD
DEVIATIO
N 

40. Standard Deviation
•Is the most important
measures of variation.
•It is also known as the
square root of the variance.
•It is the average distance of
all the scores that deviates
from the mean value.

42. POPULATION STANDARD
DEVIATION

43. AMPLE STANDARD
DEVIATION

44. 1. Solve the mean value.
2. Subtract the mean value from each score.
3. Square the difference between the mean and
each score.
4. Find the sum of step 3.
5. Solve for the population standard deviation or
sample standard deviation using the formula for
ungrouped data.

45. EXAMPLE
X X - X (X – X)²
19 4.4 19.36
17 2.4 5.76
16 1.4 1.96
16 1.4 1.96
15 0.4 0.16
14 -0.6 0.36
14 -0.6 0.36
13 -1.6 2.56
12 -2.6 6.76
10 -4.6 21.16
Ʃx= 146 Ʃ(x-x)²= 60.40
x= 14.6

46. POPULATION STANDARD
DEVIATION

47. SAMPLE STANDARD
DEVIATION

48. Formula
of
Standar
d
Deviatio
n of
Groupe
d Data

49. POPULATION STANDARD
DEVIATION

50. SAMPLE STANDARD
DEVIATION

51. Steps in solving the STANDARD
DEVIATION of GROUP DATA
1. Solve the mean value.
2. Subtract the mean value from each midpoint or class
mark.
3. Square the difference between the mean value and
midpoint or class mark.
4. Multiply the squared difference and the corresponding
class frequency.
5. Find the sum of the results in step 4.
6. Solve the population standard deviation or sample
standard deviation using the formula for grouped data.

52. EXAMPLE
x f x
15-20 3 17.5 52.5 33.7 -16.2 262.44 787.32
21-26 6 23.5 141 33.7 -10.2 104.04 624.24
27-32 5 29.5 147.5 33.7 -4.2 17.64 88.2
33-38 15 35.5 532.5 33.7 1.8 3.24 48.6
39-44 8 41.5 332 33.7 7.8 60.84 486.72
45-50 3 47.5 142.5 33.7 13.8 190.44 571.32
n=
40 = 1348
Ʃf (Xm-X)²=
2606.4

53. POPULATION STANDARD
DEVIATION