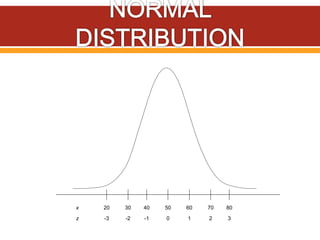
Z-scores, also called standard scores, measure how many standard deviations a raw score is above or below the mean of its distribution. A z-score indicates where a particular score lies in relation to all other scores in the distribution. To calculate a z-score, the raw score is subtracted from the mean and divided by the standard deviation of the distribution. Z-scores can be positive, negative, or zero, depending on whether the raw score is above, below, or equal to the mean. Several examples are provided to demonstrate calculating z-scores from raw scores, means, and standard deviations.

1.  
Mirasol S. Madrid III-9 BS Psychology

2. Also called as z scores
Measures the difference
between the raw score and the
mean of the distribution using
standard deviation of the
distribution as a unit of

3. Reflects how many
standard deviations above
or below the mean a raw
score is

4. By itself, a raw score or X
value provides very little
information about how that
particular score compares
with other values in the
distribution.

5. A score of X = 53, for
example, may be a
relatively low score, or an
average score, or an
extremely high score
depending on the mean and
standard deviation for the
distribution from which the
score was obtained.

6. 50 60 70 80403020
0 1 2 3-1-2-3
x
z

7. If the raw score is
transformed into a z-score,
however, the value of the z-
score tells exactly where the
score is located relative to
all the other scores in the
distribution.

8. 𝑧 =
(𝑥 − 𝑥)
𝑠
Where:
Z = standard score/z-score
X = Raw Score
𝒙 = Mean
S = Standard Deviation

9. 𝑧 =
(𝑥 − 𝜇)
𝜎
Where:
Z = standard score/z-score
X = Raw Score
𝝁 = Mean
𝝈 = (sigma) Standard Deviation

10. Z-scores can be positive
(above the mean),
negative (below the
mean), or zero (equal to
the mean)

11. 

12. In a distribution of
statistic test score,
having the mean of 75
and a standard deviation
of 10, find the z score,
scoring 85

13. X = 85
𝑥 = 75
S = 10

14. 1. Step 1
𝑧 =
(85 − 75)
10
2. Step 2
𝑧 =
(10)
10
z = 1

15. A score of 85 is one (1)
standard deviation
above the mean

16. 

17. Find the Z score of 60
having a mean of 75
and a standard
deviation of 10

18. X = 60
𝑥 = 75
S = 10

19. 1. Step 1
𝑧 =
(55 − 75)
10
2. Step 2
𝑧 =
(−20)
10
z= -2

20. A score of 60 is two (2)
standard deviation
below the mean

21. 

22. X = 100
𝑥 = 100
S = 10

23. 1. Step 1
𝑧 =
(100 − 100)
10
2. Step 2
𝑧 =
(0)
10
z= 0

24. A score of 100 is falls
on the given mean.

25. 

26. 1. X = 58, µ = 50, σ = 10
2. X = 74, µ = 65, σ = 6
3. X = 47, µ = 50, σ = 5
4. X = 87, µ = 100, σ = 8
5. X = 22, µ = 15, σ = 5

27. 1. z = +.8
2. z = +1.5
3. z = -.6
4. z = -1.625
5. z = +1.4