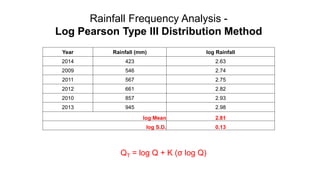
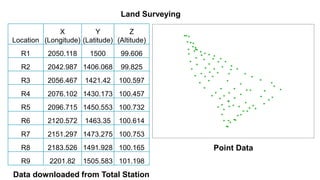
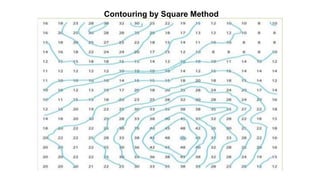
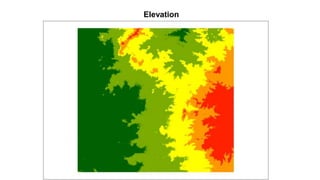
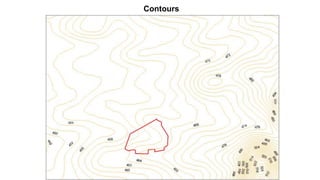
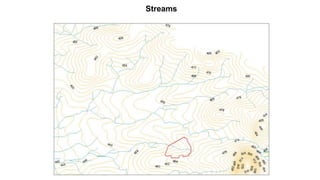
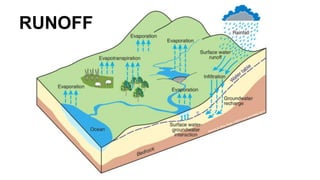
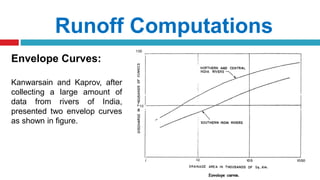
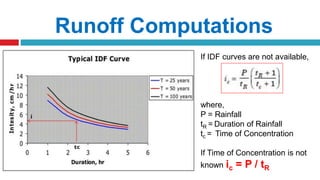
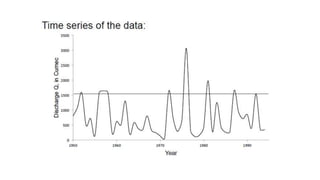
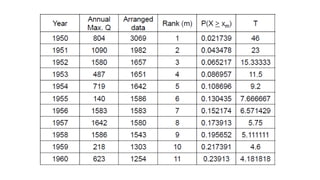
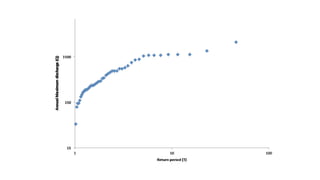
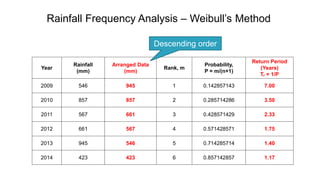
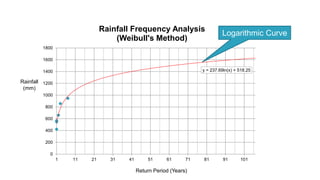
The document outlines methodologies for watershed management, including delineation, runoff computation, and flood frequency analysis. It describes various methods for estimating runoff, such as empirical formulae and the rational method, as well as techniques for flood frequency analysis, including the Weibull, Gumbel, and Log Pearson methods. Emphasis is placed on the significance of understanding watershed behavior and hydrological statistics in managing flood risks.

1. RUNOFF & FLOOD FREQUENCY
ANALYSIS
(WATERSHED MANAGEMENT)
UNIT – III
Rambabu Palaka, Assistant ProfessorBVRIT

2. Learning Objectives
1. Watershed Delineation
a) Data Collection
b) Preparation of Contours
c) Watershed Delineation
2. Runoff Computations from a Watershed
a) Empirical Formulae
b) Rational Method
c) SCS-CN Method
3. Flood Frequency Analysis
a) Weibull Method
b) Gumbell Method
c) Log Pearson Method

3. Watershed Delineation
Delineation is a process of dividing the watershed into discrete
land and channel segments to analyze watershed behavior.
It means drawing lines on a map to identify a watershed’s
boundaries. These are typically drawn on topographic maps
using information from contour lines.
Contour lines are lines of equal elevation, so any point along a
given contour line is the same elevation.

4. Watershed Delineation
Source of Data:
 Toposheets from Survey of India
 Digital Elevation Model (DEM)
DEM:
It is a digital model or 3D representation of a terrain's surface created from terrain
elevation data which can be obtained through
a) Land Surveying using Auto Level, Theodolite, Total Station, GPS, DGPS etc.
b) Remote Sensing
a) Aerial Photography
b) LIDAR (Light Detection And Ranging) that measures distance by
illuminating a target with a laser and analyzing the reflected light.
c) Satellite Images eg. CartoDEM

5. LAND SURVEYING
(Total Station, GPS, DGPS)

6. Location
X
(Longitude)
Y
(Latitude)
Z
(Altitude)
R1 2050.118 1500 99.606
R2 2042.987 1406.068 99.825
R3 2056.467 1421.42 100.597
R4 2076.102 1430.173 100.457
R5 2096.715 1450.553 100.732
R6 2120.572 1463.35 100.614
R7 2151.297 1473.275 100.753
R8 2183.526 1491.928 100.165
R9 2201.82 1505.583 101.198
Data downloaded from Total Station
Point Data
Land Surveying

7. Contouring by Square Method

8. Contours (Vector Data)
3D Digital Model
Land Surveying

9. REMOTE SENSING

10. CartoDEM (30 m resolution) – Raster Data
Cartosat-1 was launched by PSLV-C6
on 5 May 2005
from Satish Dhawan Space Centre at Sriharikota

11. CartoDEM (30 m resolution)

12. Hillshade

13. Elevation

14. Contours

15. Streams

16. Streams

17. 3D Model

18. RUNOFF

19. Runoff Computations
Heavy losses and huge damages taking place in a watershed
due to occurrence of flood.
Flood is produced due to heavy rainfall and its estimation is
dependent on
 Rainfall Intensity
 Type of soil
 Shape and size of watershed
 Conditions of watershed at the time of rainfall
 Slope of waterway

20. Runoff Computations
Methods of Estimation of Runoff:
1. Empirical Formulae
2. Envelope Curve
3. Physical Indication of Past Floods
4. Rational Method
5. Probable Maximum Precipitation (PMP) Chart
6. Rating Curve
7. Unit Hydrograph Method
8. SCS-CN Method
9. Flood Frequency Analysis

21. Runoff Computations
Empirical Formulae:
1. Dicken’s formula
Q = CA3/4
Where,
Q = Design Flood (m3/s)
A = Area of Catchment in KM2
C = Dicken’s Constant
North Indian Plains 6
North Indian Hilly Regions 11-14
Central India 14-28
Coastal Andhra & Orissa 22-28

22. Runoff Computations
Empirical Formulae:
2. Ryve’s formula
Q = CA2/3
Where,
Q = Design Flood (m3/s)
A = Area of Catchment in KM2
C = Ryve’s Constant
Areas within 80 km from east coast 6.8
Areas within 80-160 km from east coast 8.5
Limited areas near hills 10.2

23. Runoff Computations
Empirical Formulae:
3. Inglis formula
Where,
Q = Design Flood (m3/s)
A = Area of Catchment in KM2
It is based on data of watershed in Western Ghats in Maharastra
10.4A
A124
Q



24. Runoff Computations
Major Limitation of using Empirical
Formulae is the subjective decision about
the values C to be adopted

25. Runoff Computations
Envelope Curves:
Kanwarsain and Kaprov, after
collecting a large amount of
data from rivers of India,
presented two envelop curves
as shown in figure.

26. Runoff Computations
Physical Indication of Past Floods:
Ancient monuments situated near the banks of river always bear the marks or
records of the past floods.
The flood discharge is obtained from the Formula, Q = A.V
Where
A = Cross section of Valley during dry season
V = Velocity of flow can be calculated from Manning’s N
Usually, factor of safety about 1.5 is used to obtain maximum flood

27. Runoff Computations
Rational Method:
It is most effective in urban areas with drainage areas of less than 200 acres. The
method is typically used to determine the size of storm sewers, channels, and other
drainage structures.
Q = (C.I.A) / 3.6
Where
C = Runoff Coefficient
I = Rainfall Intensity in mm/h
A = Area of Catchment in KM2
Note: Rainfall Intensity (i) can be found from the Intensity–Duration–Frequency
(IDF) curves corresponding to Time of Concentration and Return Period

28. Runoff Computations
If IDF curves are not available,
where,
P = Rainfall
tR = Duration of Rainfall
tc = Time of Concentration
If Time of Concentration is not
known ic = P / tR

29. Runoff Computations
Runoff Co-efficient (C):

30. Runoff Computations
Rational Method:
Assumptions:
 The drainage basin characteristics are fairly
homogeneous
 Rainfall duration equal to the time of concentration
results in the greatest peak discharge
The time of concentration is the time required for runoff
to travel from the most distant point of the watershed to
the outlet.
Time of Concentration, tc = Hydraulic Length / Velocity

31. Runoff Computations
Rational Method:
Time of Concentration can be found using

32. Runoff Computations
Probable Maximum Precipitation Chart:
PMP Charts have been prepared by Meteorological Department of India for some
states such as Punjab, Haryana, Delhi and Rajasthan using following methods.
1. Meteorological method
2. Statistical Study of Rainfall data,
PMP = Avg. Rainfall + K.σ
where
K = Frequency Factor depends on statistical distribution series, no. of years
record and the return period.
σ = Standard Deviation

33. Runoff Computations
Rating Curve:
It is a graph of discharge versus stage for a given point on a stream, usually at
gauging stations, where the stream discharge is measured across the stream
channel with a flow meter.

34. Runoff Computations
Unit Hydrograph Method:
It is a linear model of the catchment which is used to find out the volume of direct
surface runoff (DSR) due to 1 cm of rainfall excess. If rainfall comes to the
catchment producing 2 cm of excess rainfall, the ordinates of the DSR will be twice
as much as the UH ordinates and volume of DSR will be two times of the volume of
unit hydrograph.
Assumptions:
1. The rainfall is of spatially uniform intensity with in its specified time
2. The effective rainfall is uniformly distributed throughout the whole area of
drainage basin

35. Runoff Computations
Unit Hydrograph Method:

36. Runoff Computations
SCS – CN Method:
The curve number method was developed by the USDA Natural Resources
Conservation Service, which was formerly called the Soil Conservation Service or
SCS.
The curve number is based on the area's hydrologic soil
group, land use, treatment and hydrologic condition.

37. Runoff Computations
SCS – CN Method:
Where
P = Rainfall
Ia = Initial Abstractions
S = Potential maximum retention after runoff begins

38. Hydrologic Soil Groups:
HSG Group A (low runoff potential): Soils with high infiltration rates
even when thoroughly wetted. (final infiltration rate greater than 0.3
inches/hour).
HSG Group B: Soils with moderate infiltration rates when thoroughly
wetted. (final infiltration rate of 0.15 to 0.30 inches/hour)
HSG Group C: Soils with slow infiltration rates when thoroughly wetted.
(final infiltration rate 0.05 to 0.15 inches/hour)
HSG Group D (high runoff potential): Soils with very slow infiltration
rates when thoroughly wetted. (final infiltration rate less than 0.05
inches/hour).

41. FLOOD FREQUENCY ANALYSIS
(Estimation of Design Flood)

42. Flood Frequency Analysis
Return Period:
A return period, also known as a recurrence interval (sometimes repeat
interval) is an estimate of the likelihood of flood or a river discharge flow to
occur.
For example, a 10 year flood has a 1/10=0.1 or 10% chance of being
exceeded in any one year. This does not mean that if a flood with such a
return period occurs, then the next will occur in about ten years' time -
instead, it means that, in any given year, there is a 10% chance that it will
happen, regardless of when the last similar event was.

43. Flood Frequency Analysis
Return Period is a statistical measurement typically based on historic data
and is usually used for risk analysis (e.g. to decide whether a project should
be allowed to go forward in a zone of a certain risk, or to design structures
to withstand an event with a certain return period).
Methods:
1. Weibull Method
2. Gumbell Method
3. Log Pearson Method

44. Flood Frequency Analysis
Weibull Method
In probability theory and statistics, it is a continuous probability distribution
 Most commonly used method
 If ‘n’ values are distributed uniformly between 0 and 100 percent
probability, then there must be n+1 intervals, n–1 between the data
points and 2 at the ends.
Probability, P = m / n+1
where, m = rank

50. Year
Rainfall
(mm)
Arranged Data
(mm)
Rank, m
Probability,
P = m/(n+1)
Return Period
(Years)
Tr = 1/P
2009 546 945 1 0.142857143 7.00
2010 857 857 2 0.285714286 3.50
2011 567 661 3 0.428571429 2.33
2012 661 567 4 0.571428571 1.75
2013 945 546 5 0.714285714 1.40
2014 423 423 6 0.857142857 1.17
Rainfall Frequency Analysis – Weibull’s Method
Descending order

51. y = 237.69ln(x) + 518.25
0
200
400
600
800
1000
1200
1400
1600
1800
1 11 21 31 41 51 61 71 81 91 101
Rainfall Frequency Analysis
(Weibull's Method)
Rainfall
(mm)
Return Period (Years)
Logarithmic Curve

52. Flood Frequency Analysis
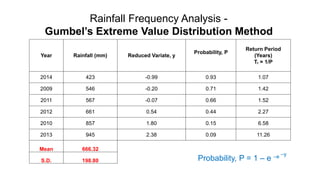
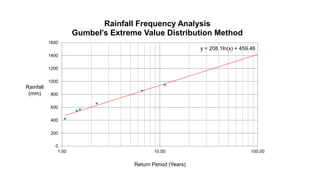
Gumbel’s Extreme Value Distribution Method:
E.J. Gumbel in 1941 was consider that annual flood peaks are extreme values of
floods in each of the annual series of recorded data. Hence, floods follow the
extreme value distribution.
Probability, P = 1 – e –e –y
Return Period, T = 1/P
Where
y = reduced variate = [1.282 (Q – Q) / σ] + 0.577
e = base of Naperian Logarithm

53. Flood Frequency Analysis
Gumbel’s Extreme Value Distribution Method:
Flood Magnitude for a given Return Period, QT = Q + KT σ
Where
Frequency Factor,
T = Return Period
Q = Mean
σ = Standard Deviation

54. Rainfall Frequency Analysis -
Gumbel’s Extreme Value Distribution Method
Year Rainfall (mm) Reduced Variate, y
Probability, P
Return Period
(Years)
Tr = 1/P
2014 423 -0.99 0.93 1.07
2009 546 -0.20 0.71 1.42
2011 567 -0.07 0.66 1.52
2012 661 0.54 0.44 2.27
2010 857 1.80 0.15 6.58
2013 945 2.38 0.09 11.26
Mean 666.32
S.D. 198.80 Probability, P = 1 – e –e –y

55. y = 208.1ln(x) + 459.46
0
200
400
600
800
1000
1200
1400
1600
1.00 10.00 100.00
Rainfall Frequency Analysis
Gumbel’s Extreme Value Distribution Method
Return Period (Years)
Rainfall
(mm)

56. Flood Frequency Analysis
Log Pearson Type III Distribution Method:
Person (1930) developed this method. In this method, it is recommended to convert
the data series to logarithms and then compute the following.
1. Compute Logarithms of flow log Q
2. Estimate Average of log Q
3. Compute Standard Deviation σ log Q
4. Compute Skew Coefficient,
Cs = (N Σ (log Q – log Q)3) / (N-1)(N-2) (σ log Q)3
5. QT = log Q + K (σ log Q)
where K = log Pearson Frequency Factor based on Cs & Return Period

57. Year Rainfall (mm) log Rainfall
2014 423 2.63
2009 546 2.74
2011 567 2.75
2012 661 2.82
2010 857 2.93
2013 945 2.98
log Mean 2.81
log S.D. 0.13
Rainfall Frequency Analysis -
Log Pearson Type III Distribution Method
QT = log Q + K (σ log Q)

58. Reference
Watershed Management
by
Madan Mohan Das
Mimi Das Saikia
PHI Learning Private Limited