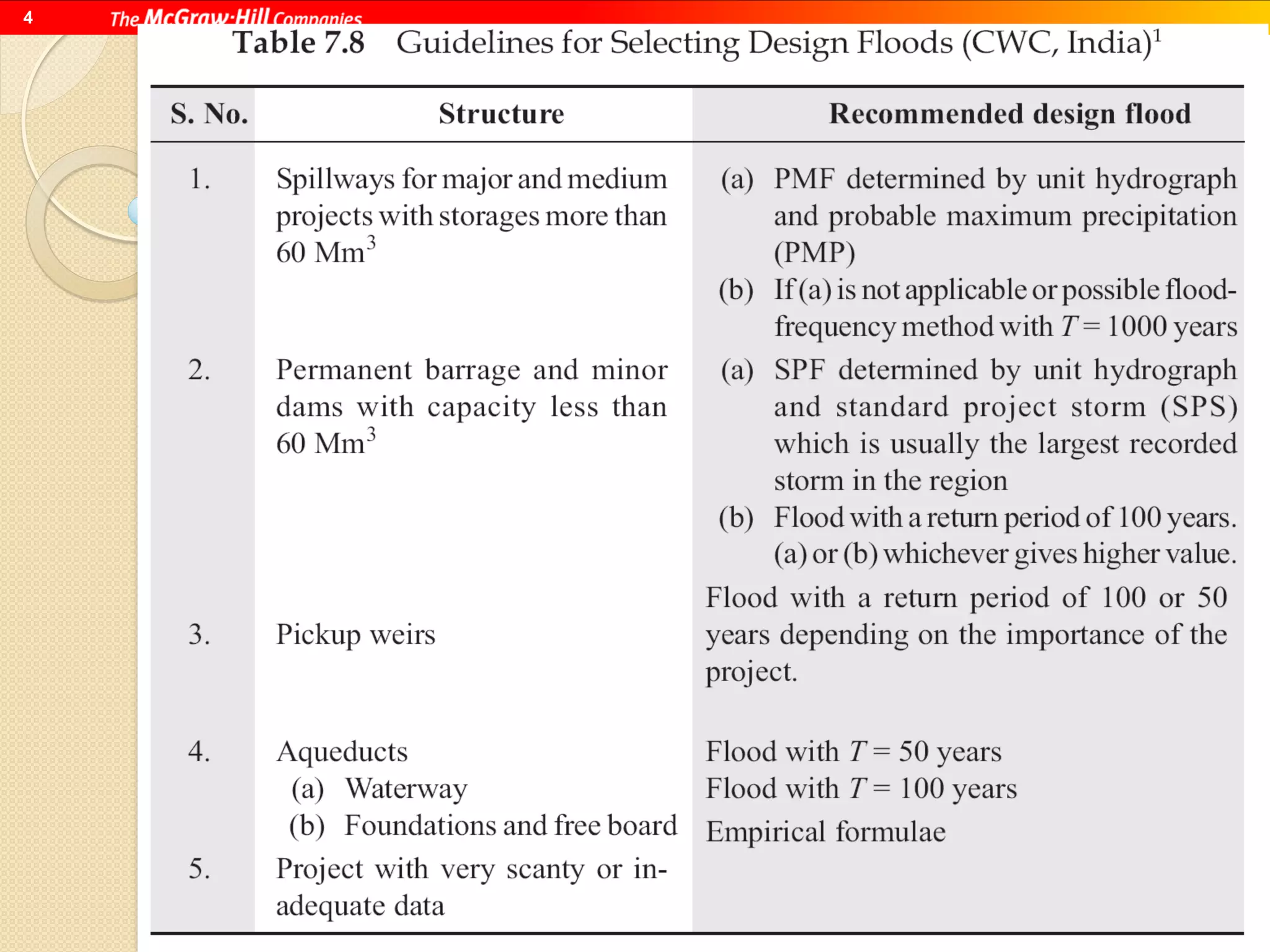
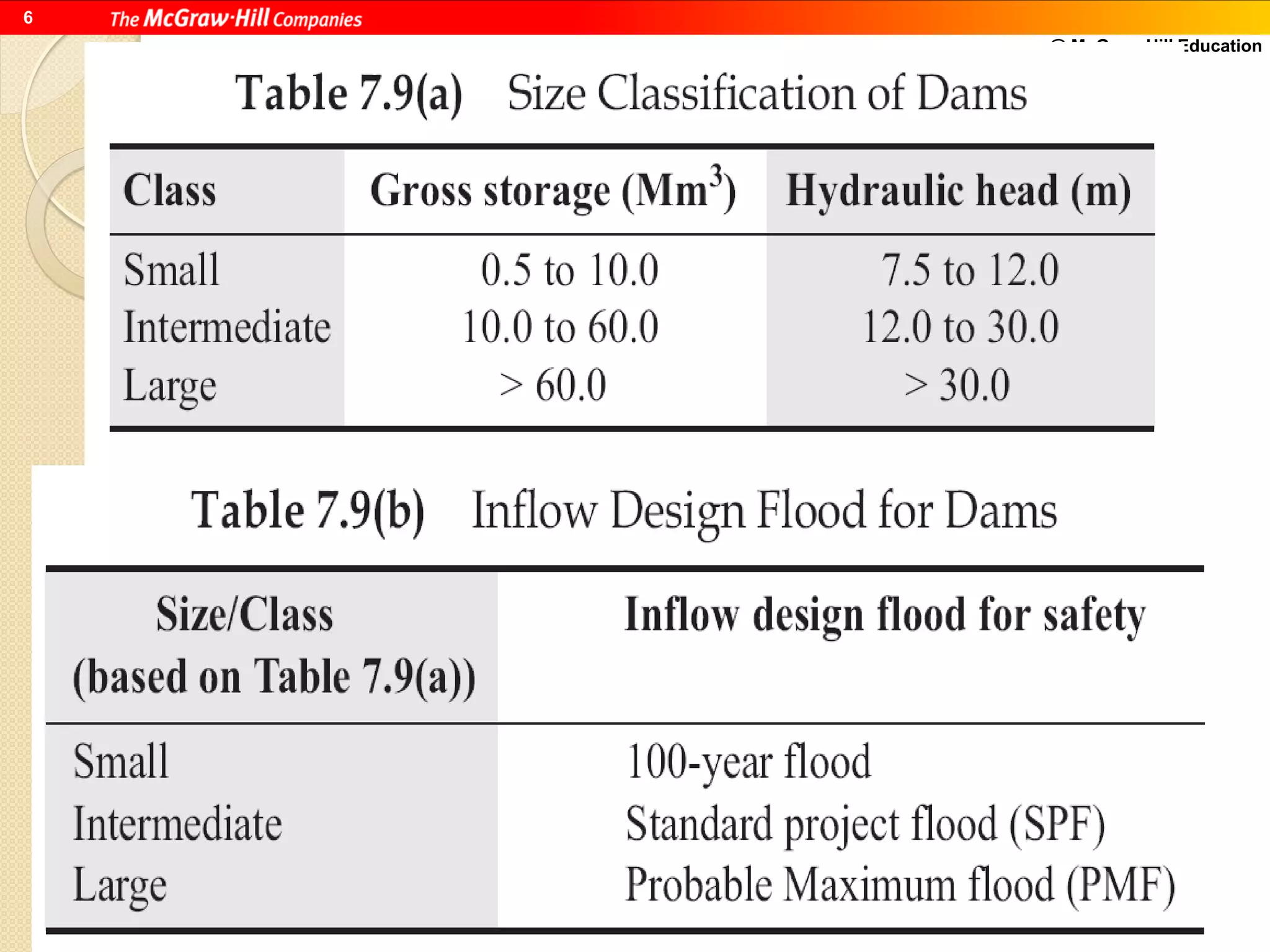
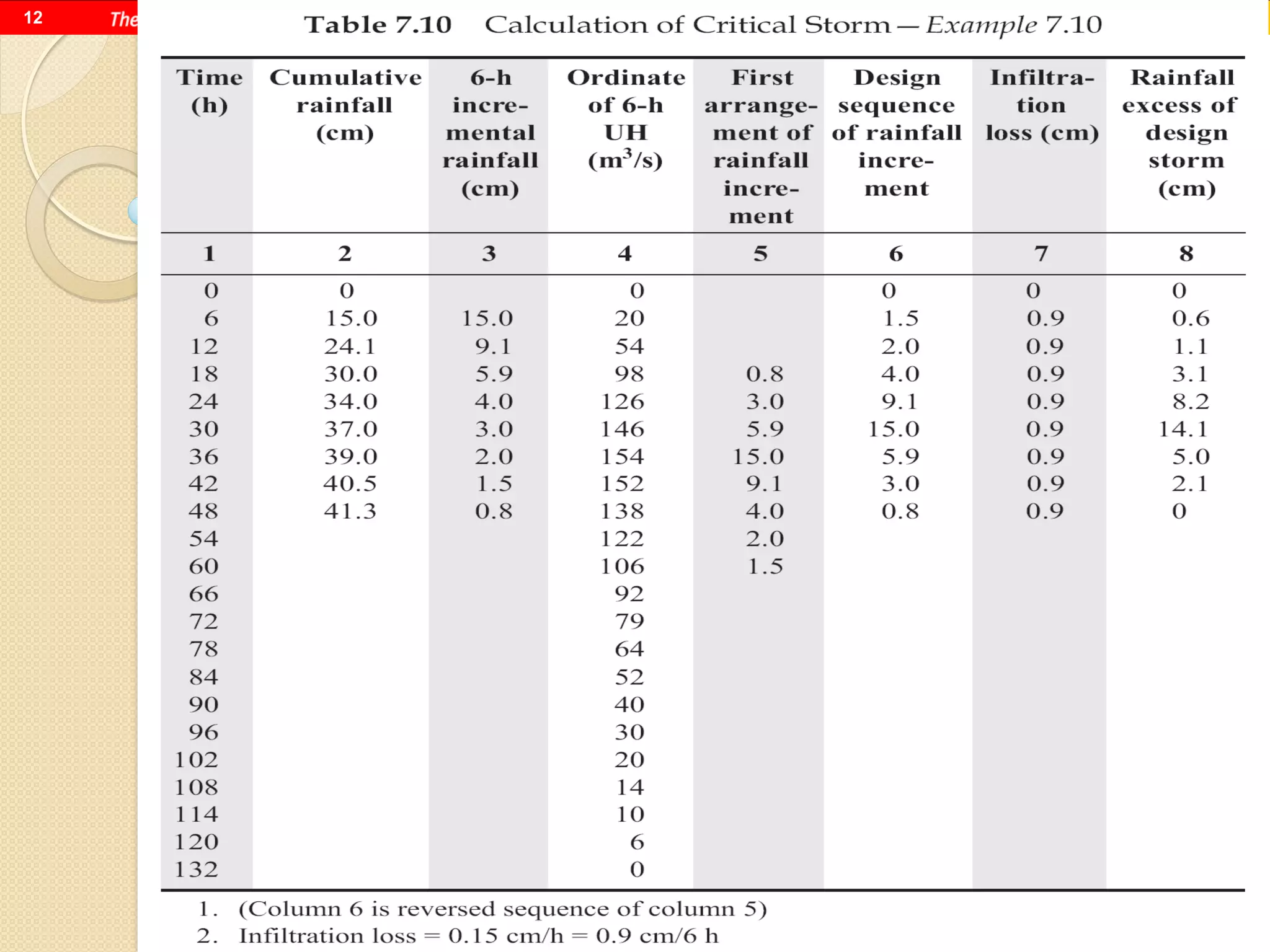
This document discusses methods for selecting design floods for hydraulic structures. It describes three types of design floods: spillway design flood, standard project flood, and probable maximum flood. The spillway design flood is used for spillway design. The standard project flood results from extreme but plausible meteorological conditions. The probable maximum flood represents the physically possible worst case flood. The document also provides examples of calculating design floods using the Gumbel method and defines safety factors and margins of safety for flood discharge estimates.

1. @ McGraw-Hill Education
1
7.11 - DESIGN FLOOD
 For economic consideration, it’s not practical to
design the hydraulic structure for safety purpose
against maximum possible flood all the times
Culverts / storm drainage can be designed for less severe
flood
 This section show the procedure to select the
flood magnitude for the design of hydraulic
structure
 3Types
Spillway design flood
Standard project flood (SPF)
Probable maximum flood (PMF)

2. @ McGraw-Hill Education
2
• Spillway design flood
Design flood specific for designing spillway of storage
structure
This term is used to donate maximum discharge that can
passed in hydraulic structure without causing damage or
threat to the stability of structure
• Standard project flood (SPF)
Flood that result from combination of meteorological &
hydrological factors
Extreme rare combination of factors are excluded
Used in situation where failure would cause less damage
40% - 60% of PMF for same drainage basin

3. @ McGraw-Hill Education
3
•Probable maximum flood (PMF)
Extreme flood that physically possible from severe
combination,
including rare combination of meteorological &
hydrological combination
Used in situation where failure of structure cause life
and severe damage
 Table 7.8
Guideline for selecting design flood
Adopted by CWC India

4. @ McGraw-Hill Education
4

5. @ McGraw-Hill Education
5
INDIAN STANDARD GUIDELINE
FOR DESIGN OF FLOOD FOR
DAMS
 Classification of dams
According to size (table 7.9(a))
By using hydraulic heads & gross storage
• Hydraulic head define as
Difference between maximum water level on
upstream & normal annual average flood level
downstream
• For safety of dam
The inflow design flood (IDF) is considered
Given byTable 7.9 (b)

6. @ McGraw-Hill Education
6

7. @ McGraw-Hill Education
7
7.12 – DESIGN STORM
 To estimate the design flood by using unit
hydrograph
• Computation of design storm
By hydrometeorologist by using meteorological data
Various method use which depend on availability of
reliable data and expertise
 2 method
Storm-producing probable maximum
precipitation (PMP) derived from PMF
Standard project storm (SPS) for SPF calculation

8. @ McGraw-Hill Education
8
 Below show procedure from India
1. Find the critical rainfall.
This will be the basin lag if the flood peak is of
interest
If flood volume is of interest, find duration of the
longest storm experienced in the basin
2. Find the past major storm
DAD analysis is performed and the enveloping
curve represent max depth-duration relation for
the study is obtained

9. @ McGraw-Hill Education
9
3. From enveloping curve
Find the rainfall depth for convenient time
intervals (eg. 6 hr)
Increment to be arranged in order to find critical
sequence which produce max flood peak when
applied to unit hydrograph
Critical sequence find by
 trail & error
Increment of precipitation arranged by
I. Maximum rainfall increment is against
maximum unit hydrograph ordinate
II. Second highest rainfall increment is against
the second largest unit hydrograph ordinate
III. The sequence of rainfall increment
arranged from I & II is reversed ( eg 7.8)

10. @ McGraw-Hill Education
10
4. Combine design storm & abstraction most
conducive to high runoff
 Low initial loss & lowest infiltration rate to get to
hyetograph of rainfall excess to operate on unit
hydrograph

11. @ McGraw-Hill Education
11
Eg 7. 10
 The ordinates of cumulative rainfall from
the enveloping maximum depth-duration
curve of a basin are given below.Also given
are the ordinates of a 6-h unit hydrograph.
Design the critical sequence of rainfall
excesses by taking the ø index to be 0.15
cm/h

12. @ McGraw-Hill Education
12

13. @ McGraw-Hill Education
13
 Given data
Column 1,2 & 4
• Column 2
Row 2 – row 1 = 15 – 0 = 15
Row 3 – row 2 = 24.1 – 15 = 9.1
• Column 5
Max data in col. 3 is pair with col.4
• Column 6
Reversed of column 5
• Column 7
Given data infiltration loss = 0.15 cm/h x 6h
= 0.9 cm/6h
• Column 8
Column 6 – column 7

14. @ McGraw-Hill Education
14
7.13 – RISK, RELIABILITY AND
SAFETY FACTORS
 Design of hydraulic structure involve uncertainty &
such involve risk of failure
 Risk, Rˉ is the probability of occurrence of an
event (x≥xt) at least once over n successive year
 Rˉ = 1 – (probability of non-occurrence of the
event x ≥ xt in n years )
 P = probability P (x ≥ xt) = 1/T
 T = return period
• Reliability, Re = 1 - Rˉ = (1 – 1/T)^n
Rˉ = 1 – ( 1 – P ) ^ n ( equ 7.29)
= 1 – ( 1 - 1/T) ^ n

15. @ McGraw-Hill Education
15
 Safety factor
Due to uncertainty in water resource development
project such as during constructional of the building or
from economic causes
A safety factor with parameter M is apply to the
development project
Parameter, M
Includes items such as flood discharge magnitude,
max. river stage, reservoir capacity and free board
Safety margin is the difference between Cam & Chm
(Cam – Chm)
Actual values of parameter
M adopted in the
Safety factor = (SF)m = design of projects . = Cam
( for parameter M) Values of parameters M Chm
obtained from
hydrological consideration

16. @ McGraw-Hill Education
16
Eg. 7.11
 A bridge has an expected life of 25 years and is
designed for flood magnitude of return period 100
years
a) what is the risk of this hydrological design
b) if a 10% risk is acceptable, what return period
will have to be adopted
• Solution :
a) Given n = 25 years
T = 100 years
Using equation 7.29

17. @ McGraw-Hill Education
17
.
R = 1 – ( 1 - 1/ T) ^ n
= 1 – ( 1 – 1/100) ^ 25
= 0.222
Hence, inbuilt risk design is 22.2 %
.
b) Given R = 10% = 0.10
0.10 = 1 – ( 1 – 1/T)^25
T = 238 years ≈ 240 years
Hence, for 10 % risk, the bridge must be design with
240 years of return period

18. @ McGraw-Hill Education
18
Eg. 7. 12
 Analysis of annual flood series of a river yielded a
sample mean of 1000 m^3/s and standard deviation
of 500m^3/s. estimate the design flood of a
structure on this river to provide 90% assurance
that the structure will not fail in the next 50 years.
Use Gumbel method and assume samples size is
large

19. @ McGraw-Hill Education
19
 Solution:
Given
xˉ = 1000 m^3/s
σn-1 = 500 m^3/s
Reliability, Re = 90% = 0.9
n = 50 year
 We need to find xt
xt = xˉ + Kσn-1
yt = - (ln x ln( T /( T -1) )
K = (yt – 0.588) / 1.2825

20. @ McGraw-Hill Education
20
Re = ( 1 – 1/T)^n
0.90 = (1 – 1/T)^50
T = 0.998 = 475 years
yt = - (ln x ln( T /( T -1) )
= - (ln x ln ( 475 / (475 – 1))
= 6.16226
K = (yt – 0.588) / 1.2825
= 4.355
xt = xˉ + Kσn-1 = 3177 m^3/s

21. @ McGraw-Hill Education
21
Eg 7.13
 Annual flood data of the river Narmada at
Garudeshwar covering the period of 1948 to 1979
yield for annual flood discharge a mean of 29,600
m^3/s & standard deviation of 14,860 m^3/s. For a
proposed bridge on this rover this site it is decided
to have an acceptable risk of 10% in its expected
life of 50 years
a) estimate flood discharge by Gumbel Method
b) if the actual flood values in this design is
125,000m^3/s, what are the safety factor and safety
margin relating to the maximum flood discharge

22. @ McGraw-Hill Education
22
 Solution
Given
Rˉ= 10% = 0.1
n = 50 year
N = 32 years (1948 – 1979)
Hence R ˉ = 1 – ( 1 - 1/ T) ^ n
0.1 = 1 – ( 1 - 1/ T) ^ 50
T =475 years
From tables 7.3 & 7.4
y ˉn =0.5380
Sn = 1.1193

23. @ McGraw-Hill Education
23
yt = - (ln x ln( T /( T -1) )
= - (ln x ln ( 475 / (475 – 1))
= 6.16226
K = (yt – y ˉn ) / Sn
= 5.0248
xt = xˉt + Kσn-1 = 29600 + ( 5.0248 x 14860)
= 104568 ≈ 105000m^3/s
Safety factor, (SF)flood = 125000/105000 = 1.19
Safety margin = 12500 - 105000 = 20000m^3/s