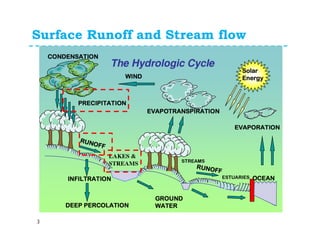
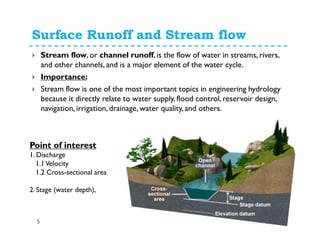
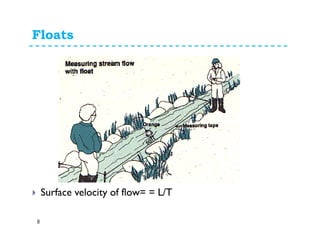
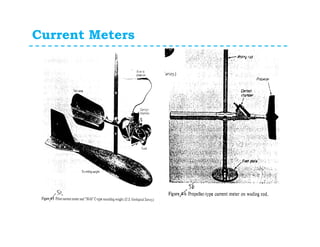
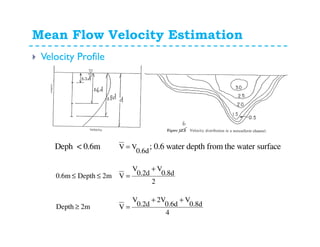
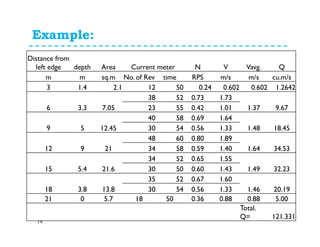
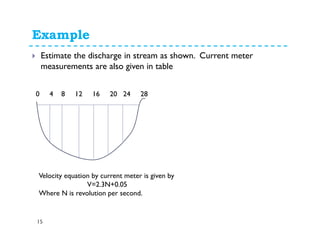
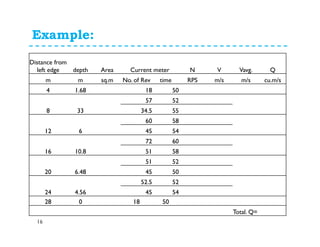
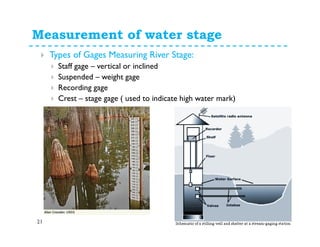
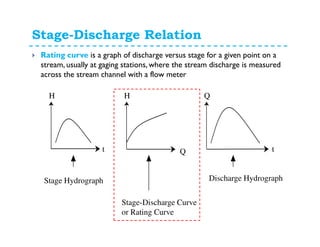
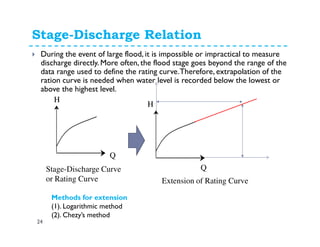
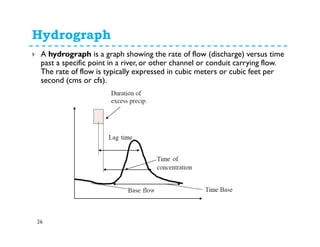
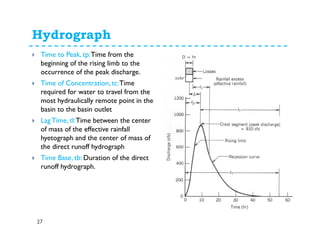
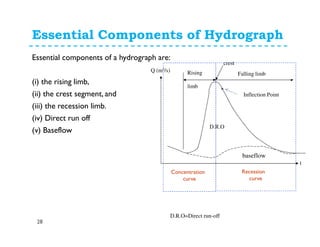
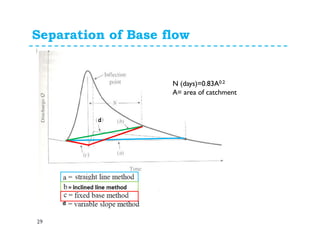
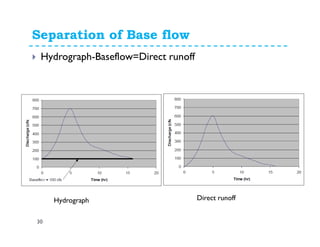
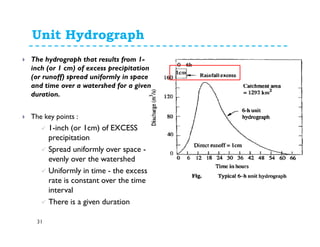
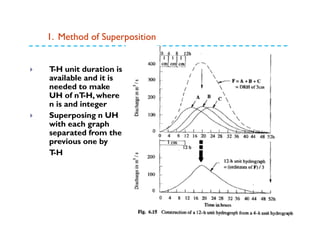
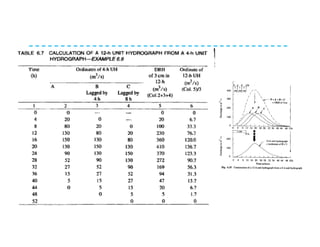
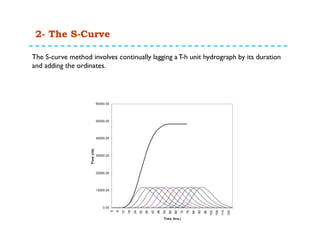
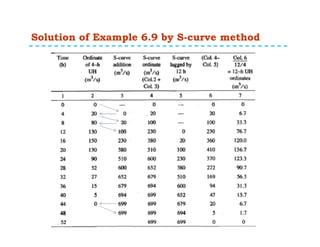
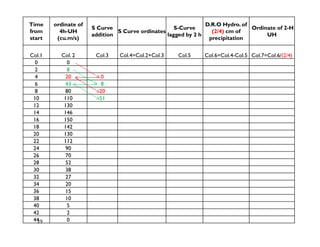
This document discusses surface runoff, stream flow, hydrographs, and unit hydrographs. It begins by defining surface runoff and stream flow, explaining that surface runoff occurs when precipitation is unable to infiltrate the ground and flows overland into streams, rivers, and other bodies of water. It then discusses measuring stream flow through various methods like current meters and weirs to determine discharge. The document introduces the concept of hydrographs, which plot discharge over time, and unit hydrographs, which represent the hydrograph resulting from 1 unit of excess precipitation. It provides examples of using unit hydrographs and the S-curve method to develop hydrographs of different durations.

1. Runoff, Stream flow, Concept of unit
hydrograph and S-curve
Dr. Mohsin Siddique
Assistant Professor
Dept. of Civil & Env. Engg
1

2. Outcome of Lecture
2
After completing this lecture…
The students should be able to:
Understand surface runoff and its categories
Understand the concept stream flow, velocity and discharge
Understand the concept of hydrograph, unit hydrograph and its
application
Understand the application of rational formula and its
application

3. Surface Runoff and Stream flow
3

4. Surface Runoff and stream flow
4
On hard or frozen ground, most of the precipitation is unable to seep
below ground.This precipitation then flows down slopes and hills,
eventually stopping in rivers, lakes, streams, and oceans.
Some of this water will then evaporate and rejoin the hydrologic cycle,
while other water will remain in the body of water.
This process of water traveling over the ground and collecting in a body of
water is called surface runoff.
Stream

5. Surface Runoff and Stream flow
5
Stream flow, or channel runoff, is the flow of water in streams, rivers,
and other channels, and is a major element of the water cycle.
Importance:
Stream flow is one of the most important topics in engineering hydrology
because it directly relate to water supply, flood control, reservoir design,
navigation, irrigation, drainage, water quality, and others.
Point of interest
1. Discharge
1.1Velocity
1.2 Cross-sectional area
2. Stage (water depth),

6. Stream Flow Measurements (Discharge)
6
Serves as the basis for many water resources engineering designs
Measurement of Discharge;
Measurement of flow area
Measurement of flow velocity

7. Devices for Flow Velocity Measurement
Floats: Suitable for straight channel, V = L/T
PitotTubes: Suitable only for clean water
Current Meters
Cups
Propellers
V = a + b×N
whereV = flow velocity; a = starting velocity to overcome
mechanical friction; b = equipment calibration constant; N =
revolutions/sec.

8. Floats
8
Surface velocity of flow= = L/T

9. Current Meters

10. Mean Flow Velocity Estimation
Velocity Profile
Deph < 0.6m 0.6d
VV = ; 0.6 water depth from the water surface
2mDepth0.6m ≤≤
2
0.8d
V
0.2d
V
V
+
=
2mDepth ≥
4
0.8d
V
0.6d
2V
0.2d
V
V
++
=

11. Current Meters
11

12. Measurement of Stream Flow Discharge
1. Mid-Section Method
i
A
i
V
i
i
QQ
i
A
i
V
i
Q
i
bd
i
A
∑=∑=
=
=
∑=
=
+=
+
+=
+
i
i
QQ
i
A
i
V
i
Q
)V
i
V(
2
1
i
V
)
1i
d
i
(d
2
b
i
A
1i
2. Mean-Section Method

13. Example
13
Estimate the discharge in stream as shown. Current meter
measurements are also given in table
Distance from
left edge depth Current meter
m m No. of Rev Time (s)
3 1.4 12 50
6 3.3
38 52
23 55
9 5
40 58
30 54
12 9
48 60
34 58
15 5.4
34 52
30 50
18 3.8
35 52
30 54
21 0 18 50
0 3 6 9 12 15 18 21
Velocity equation by current meter is given by
V=2.3N+0.05
Where N is revolution per second.

14. Example:
14
Distance from
left edge depth Area Current meter N V Vavg. Q
m m sq.m No. of Rev time RPS m/s m/s cu.m/s
3 1.4 2.1 12 50 0.24 0.602 0.602 1.2642
6 3.3 7.05
38 52 0.73 1.73
1.37 9.6723 55 0.42 1.01
9 5 12.45
40 58 0.69 1.64
1.48 18.4530 54 0.56 1.33
12 9 21
48 60 0.80 1.89
1.64 34.5334 58 0.59 1.40
15 5.4 21.6
34 52 0.65 1.55
1.49 32.2330 50 0.60 1.43
18 3.8 13.8
35 52 0.67 1.60
1.46 20.1930 54 0.56 1.33
21 0 5.7 18 50 0.36 0.88 0.88 5.00
Total.
Q= 121.331

15. Example
15
Estimate the discharge in stream as shown. Current meter
measurements are also given in table
0 4 8 12 16 20 24 28
Velocity equation by current meter is given by
V=2.3N+0.05
Where N is revolution per second.

16. Example:
16
Distance from
left edge depth Area Current meter N V Vavg. Q
m m sq.m No. of Rev time RPS m/s m/s cu.m/s
4 1.68 18 50
8 33
57 52
34.5 55
12 6
60 58
45 54
16 10.8
72 60
51 58
20 6.48
51 52
45 50
24 4.56
52.5 52
45 54
28 0 18 50
Total. Q=

17. Measurement of Stream Flow Discharge
(3) Area-Slope Method
2/13/21
SAR
n
Q =
A= cross-sectional area
R=hydraulic radius
S= channel slope
n= Manning’s roughness coefficient

18. Measurement of Stream Flow Discharge
(4) Chemical dilution method
(5) Hydraulic structures

19. Hydraulic Structures for Discharge
Measurement

20. Measurement of Water Stage
20
Measurement of Water Stage
Water stage: the elevation above some arbitrary datum of
water surface at a station.

21. Measurement of water stage
21
Types of Gages Measuring River Stage:
Staff gage – vertical or inclined
Suspended – weight gage
Recording gage
Crest – stage gage ( used to indicate high water mark)

22. Measurement of Water Stage
22

23. Stage-Discharge Relation
Rating curve is a graph of discharge versus stage for a given point on a
stream, usually at gaging stations, where the stream discharge is measured
across the stream channel with a flow meter
Q
HH Q
t t
Stage Hydrograph
Stage-Discharge Curve
or Rating Curve
Discharge Hydrograph

24. Stage-Discharge Relation
24
During the event of large flood, it is impossible or impractical to measure
discharge directly. More often, the flood stage goes beyond the range of the
data range used to define the rating curve.Therefore, extrapolation of the
ration curve is needed when water level is recorded below the lowest or
above the highest level.
Q
H
Stage-Discharge Curve
or Rating Curve
Q
H
Extension of Rating Curve
Methods for extension
(1). Logarithmic method
(2). Chezy’s method

25. 25
Part II

26. Hydrograph
26
A hydrograph is a graph showing the rate of flow (discharge) versus time
past a specific point in a river, or other channel or conduit carrying flow.
The rate of flow is typically expressed in cubic meters or cubic feet per
second (cms or cfs).

27. Hydrograph
27
Time to Peak, tp:Time from the
beginning of the rising limb to the
occurrence of the peak discharge.
Time of Concentration, tc:Time
required for water to travel from the
most hydraulically remote point in the
basin to the basin outlet
LagTime, tl:Time between the center
of mass of the effective rainfall
hyetograph and the center of mass of
the direct runoff hydrograph
Time Base, tb: Duration of the direct
runoff hydrograph.

28. Essential Components of Hydrograph
28
Essential components of a hydrograph are:
(i) the rising limb,
(ii) the crest segment, and
(iii) the recession limb.
(iv) Direct run off
(v) Baseflow
D.R.O
baseflow
Falling limb
crest
Rising
limb
Q (m3/s)
Concentration
curve
Recession
curve
Inflection Point
t
D.R.O=Direct run-off

29. Separation of Base flow
29
N (days)=0.83A0.2
A= area of catchment

30. Separation of Base flow
30
Hydrograph-Baseflow=Direct runoff
Hydrograph Direct runoff

31. Unit Hydrograph
31
The hydrograph that results from 1-
inch (or 1 cm) of excess precipitation
(or runoff) spread uniformly in space
and time over a watershed for a given
duration.
The key points :
1-inch (or 1cm) of EXCESS
precipitation
Spread uniformly over space -
evenly over the watershed
Uniformly in time - the excess
rate is constant over the time
interval
There is a given duration

32. Unit Hydrographs of Different Duration
32
In practice the unit hydrographs of different duration are
needed. e.g., 1h- unit hydrograph, 2h-unit hydrograph, etc
Two methods are available to generate hydrograph of
different durations
1. Method of Superposition
2. the S-Curve

33. 1. Method of Superposition
T-H unit duration is
available and it is
needed to make
UH of nT-H, where
n is and integer
Superposing n UH
with each graph
separated from the
previous one by
T-H

36. 2- The S-Curve
0.00
10000.00
20000.00
30000.00
40000.00
50000.00
60000.00
0
6
12
18
24
30
36
42
48
54
60
66
72
78
84
90
96
102
108
114
120
Time (hrs.)
Flow(cfs)
The S-curve method involves continually lagging a T-h unit hydrograph by its duration
and adding the ordinates.

37. Solution of Example 6.9 by S-curve method

38. Problem
38
Time from
start
Ordinate of 4h-
UH (cu. m/s)
(Hours) cu.m/s
Col.1 Col. 2
0 0
2 8
4 20
6 43
8 80
10 110
12 130
14 146
16 150
18 142
20 130
22 112
24 90
26 70
28 52
30 38
32 27
34 20
36 15
38 10
40 5
42 2
44 0
Ordinate of 4h-Unit Hydrograph are given,
Determine
(1). Ordinate of S-Curve
(2). Ordinates of 2-h Unit Hydrograph

39. 39
Time
from
start
ordinate of
4h-UH
(cu.m/s)
S Curve
addition
S Curve ordinates
S-Curve
lagged by 2 h
D.R.O Hydro. of
(2/4) cm of
precipitation
Ordinate of 2-H
UH
Col.1 Col. 2 Col.3 Col.4=Col.2+Col.3 Col.5 Col.6=Col.4-Col.5 Col.7=Col.6/(2/4)
0 0 0 0 0
2 8 8 0 8 16
4 20 0 20 8 12 24
6 43 8 51 20 31 62
8 80 20 100 51 49 98
10 110 51 161 100 61 122
12 130 100 230 161 69 138
14 146 161 307 230 77 154
16 150 230 380 307 73 146
18 142 307 449 380 69 138
20 130 380 510 449 61 122
22 112 449 561 510 51 102
24 90 510 600 561 39 78
26 70 561 631 600 31 62
28 52 600 652 631 21 42
30 38 631 669 652 17 34
32 27 652 679 669 10 20
34 20 669 689 679 10 20
36 15 679 694 689 5 10
38 10 689 699 694 5 10
40 5 694 699 699 0 0
42 2 699 701 699 2 (0) 4 (0)
44 0 699 699 701 -2 (0) -4 (0)

40. Thank you
Questions….
40